3.4: Green’s Theorem

Learning Objectives

• Apply the circulation form of Green’s theorem.
• Apply the flux form of Green’s theorem.
• Calculate circulation and flux on more general regions.

In this section, we examine Green’s theorem, which is an extension of the Fundamental Theorem of Calculus to two dimensions. Green’s theorem has two forms: a circulation form and a flux form, both of which require region $D$ in the double integral to be simply connected. However, we will extend Green’s theorem to regions that are not simply connected.

Put simply, Green’s theorem relates a line integral around a simply closed plane curve $C$ and a double integral over the region enclosed by $C$. The theorem is useful because it allows us to translate difficult line integrals into more simple double integrals, or difficult double integrals into more simple line integrals.

Extending the Fundamental Theorem of Calculus

Recall that the Fundamental Theorem of Calculus says that

$$\int_a^b F′(x)\,dx=F(b)−F(a).$$

As a geometric statement, this equation says that the integral over the region below the graph of $F′(x)$ and above the line segment $[a,b]$ depends only on the value of $F$ at the endpoints $a$ and $b$ of that segment. Since the numbers $a$ and $b$ are the boundary of the line segment $[a,b]$, the theorem says we can calculate integral $\int_a^b F′(x)\,dx$ based on information about the boundary of line segment $[a,b]$ (Figure $\PageIndex{1}$). The same idea is true of the Fundamental Theorem for Line Integrals:

$$\int_C \mathbf \nabla f·d\mathbf r=f(\mathbf r(b))−f(\mathbf r(a)).$$

When we have a potential function (an “antiderivative”), we can calculate the line integral based solely on information about the boundary of curve $C$.

Figure $\PageIndex{1}$: The Fundamental Theorem of Calculus says that the integral over line segment $[a,b]$ depends only on the values of the antiderivative at the endpoints of $[a,b]$.

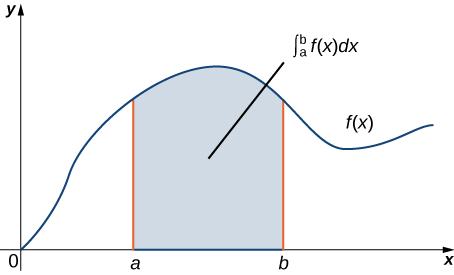
Green’s theorem takes this idea and extends it to calculating double integrals. Green’s theorem says that we can calculate a double integral over region $D$ based solely on information about the boundary of $D$. Green’s theorem also says we can calculate a line integral over a simple closed curve $C$ based solely on information about the region that $C$ encloses. In particular, Green’s theorem connects a double integral over region $D$ to a line integral around the boundary of $D$.

Circulation Form of Green’s Theorem

The first form of Green’s theorem that we examine is the circulation form. This form of the theorem relates the vector line integral over a simple, closed plane curve $C$ to a double integral over the region enclosed by $C$. Therefore, the circulation of a vector field along a simple closed curve can be transformed into a double integral and vice versa.

Green’s Theorem (Circulation Form)

Let $D$ be an open, simply connected region with a boundary curve $C$ that is a piecewise smooth, simple closed curve oriented counterclockwise (Figure $\PageIndex{2}$). Let $\mathbf F=⟨P,Q⟩$ be a vector field with component functions that have continuous partial derivatives on $D$. Then,

$$\begin{align} \oint_C \mathbf F·d\mathbf r =\oint_C P\,dx+Q\,dy \\[4pt] =\iint_D (Q_x−P_y)\,dA. \end{align}$$

Figure $\PageIndex{2}$: The image illustrates an open, simply connected region $D$ with a boundary curve $C$ that is piecewise smooth, simple, and closed, oriented counterclockwise.

Notice that Green’s theorem can be used only for a two-dimensional vector field $\mathbf F$. If $\mathbf F$ is a three-dimensional field, then Green’s theorem does not apply. Since

$$\displaystyle \int_C P\,dx+Q\,dy=\int_C \mathbf F·\mathbf T\,ds$$

this version of Green’s theorem is sometimes referred to as the tangential form of Green’s theorem.

The proof of Green’s theorem is rather technical, and beyond the scope of this text. Here we examine a proof of the theorem in the special case that $D$ is a rectangle. For now, notice that we can quickly confirm that the theorem is true for the special case in which $\mathbf F=⟨P,Q⟩$ is conservative. In this case,

$$\oint_C P\,dx+Q\,dy=0$$

because the circulation is zero in conservative vector fields. $\mathbf F$ satisfies the cross-partial condition, so $P_y=Q_x$. Therefore,

$$\iint_D (Q_x−P_y)\,dA=\int_D 0\,dA=0=\oint_C P\,dx+Q\,dy$$

which confirms Green’s theorem in the case of conservative vector fields.

Proof

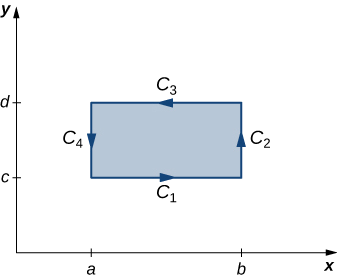
Let’s now prove that the circulation form of Green’s theorem is true when the region $D$ is a rectangle. Let $D$ be the rectangle $[a,b]×[c,d]$ oriented counterclockwise. Then, the boundary $C$ of $D$ consists of four piecewise smooth pieces $C_1$, $C_2$, $C_3$, and $C_4$ (Figure $\PageIndex{3}$). We parameterize each side of $D$ as follows:

$C_1: \mathbf r_1(t)=⟨t,c⟩$, $a≤t≤b$

$C_2: \mathbf r_2(t)=⟨b,t⟩$, $c≤t≤d$

$−C_3: \mathbf r_3(t)=⟨t,d⟩$, $a≤t≤b$

$−C_4: \mathbf r_4(t)=⟨a,t⟩$, $c≤t≤d$.

Figure $\PageIndex{3}$: A rectangle $D = [a, b] \times [c, d]$ is oriented counterclockwise, and its boundary $C$ consists of four piecewise smooth curves $C_1$, $C_2$, $C_3$, and $C_4$.

Then,

$$\begin{align*} \int_C \mathbf F·d \mathbf r &=\int_{C_1} \mathbf F·d \mathbf r+\int_{C_2} \mathbf F·d \mathbf r+\int_{C_3} \mathbf F·d \mathbf r+\int_{C_4} \mathbf F·d \mathbf r \\[4pt] &=\int_{C_1} \mathbf F·d \mathbf r+\int_{C_2} \mathbf F·d \mathbf r−\int_{−C_3} \mathbf F·d \mathbf r−\int_{−C_4} \mathbf F·d \mathbf r \\[4pt] &=\int_a^b \mathbf F( \mathbf r_1(t))· \mathbf r_1'(t)\,dt+\int_c^d \mathbf F( \mathbf r_2(t))· \mathbf r_2'(t)\,dt−\int_a^b \mathbf F( \mathbf r_3(t))· \mathbf r_3'(t)\,dt−\int_c^d \mathbf F( \mathbf r_4(t))·\mathbf r_4'(t)\,dt\\[4pt] &=\int_a^b P(t,c)\,dt+\int_c^dQ(b,t)\,dt−\int_a^bP(t,d)\,dt−\int_c^dQ(a,t)\,dt \\[4pt] &=\int_a^b(P(t,c)−P(t,d))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt\\[4pt] &=−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt. \end{align*}$$

By the Fundamental Theorem of Calculus,

$$P(t,d)−P(t,c)=\int_c^d \dfrac{\partial}{\partial y}P(t,y)dy \nonumber$$

and

$$Q(b,t)−Q(a,t)=\int_a^b \dfrac{\partial}{\partial x} Q(x,t)\,dx. \nonumber$$

Therefore,

$$−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt=−\int_a^b\int_c^d \dfrac{\partial}{\partial y} P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt. \nonumber$$

But,

$$\begin{align*} −\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt &=−\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(x,y)\,dy\,dx+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,y)\,dx\,dy \\[4pt] &=\int_a^b\int_c^d(Q_x−P_y)\,dy\,dx\\[4pt] &=\iint_D(Q_x−P_y)\,dA. \end{align*}$$

Therefore, $\displaystyle \int_C \mathbf F\cdot d\mathbf r=\iint_D(Q_x−P_y)\,dA$ and we have proved Green’s theorem in the case of a rectangle.

$\square$

To prove Green’s theorem over a general region $D$, we can decompose $D$ into many tiny rectangles and use the proof that the theorem works over rectangles. The details are technical, however, and beyond the scope of this text.

Example $\PageIndex{1}$: Applying Green’s Theorem over a Rectangle

Calculate the line integral

$$\oint_C x^2ydx+(y−3)dy, \nonumber$$

where $C$ is a rectangle with vertices $(1,1)$, $(4,1)$, $(4,5)$, and $(1,5)$ oriented counterclockwise.

Solution

Let $\mathbf F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2y,y−3⟩$. Then, $Q_x(x,y)=0$ and $P_y(x,y)=x^2$. Therefore, $Q_x−P_y=−x^2$.

Let $D$ be the rectangular region enclosed by $C$ (Figure $\PageIndex{4}$). By Green’s theorem,

$$\begin{align*} \oint_C x^2ydx+(y−3)\,dy &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D −x^2 \,dA=\int_1^5\int_1^4−x^2\,dx\,dy \\[4pt] &=\int_1^5−21\,dy=−84.\end{align*}$$

Figure $\PageIndex{4}$: The vector field with arrows representing its magnitude and direction, and a rectangular region $D$ enclosed by the boundary $C$. Key points of the rectangle, such as $(1, 1)$, $(4, 1)$, $(4, 5)$, and $(1, 5)$, are labeled. Green's Theorem simplifies the computation of the line integral by transforming it into a double integral, bypassing the need to evaluate individual line integrals along each side of the rectangle.

Analysis

If we were to evaluate this line integral without using Green’s theorem, we would need to parameterize each side of the rectangle, break the line integral into four separate line integrals, and use the methods from the section titled Line Integrals to evaluate each integral. Furthermore, since the vector field here is not conservative, we cannot apply the Fundamental Theorem for Line Integrals. Green’s theorem makes the calculation much simpler.

Example $\PageIndex{2}$: Applying Green’s Theorem to Calculate Work

Calculate the work done on a particle by force field

$$\mathbf F(x,y)=⟨y+\sin x,e^y−x⟩ \nonumber$$

as the particle traverses circle $x^2+y^2=4$ exactly once in the counterclockwise direction, starting and ending at point $(2,0)$.

Solution

Let $C$ denote the circle and let $D$ be the disk enclosed by $C$. The work done on the particle is

$$W=\oint_C (y+\sin x)\,dx+(e^y−x)\,dy. \nonumber$$

As with Example $\PageIndex{1}$, this integral can be calculated using tools we have learned, but it is easier to use the double integral given by Green’s theorem (Figure $\PageIndex{5}$).

Let $\mathbf F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨y+\sin x,e^y−x⟩$. Then, $Q_x=−1$ and $P_y=1$. Therefore, $Q_x−P_y=−2$.

By Green’s theorem,

$$\begin{align*} W &=\oint_C(y+\sin(x))dx+(e^y−x)\,dy \\[4pt] &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D−2\,dA \\[4pt] &=−2(area(D))=−2\pi (2^2)=−8\pi. \end{align*}$$

Figure $\PageIndex{5}$: The particle traverses circle $x^2+y^2=4$ exactly once in the counterclockwise direction, starting and ending at point $(2,0)$.

Exercise $\PageIndex{2}$

Use Green’s theorem to calculate line integral

$$\oint_C \sin(x^2)\,dx+(3x−y)\,dy. \nonumber$$

where $C$ is a right triangle with vertices $(−1,2)$, $(4,2)$, and $(4,5)$ oriented counterclockwise.

Hint

Transform the line integral into a double integral.

Answer

$\dfrac{45}{2}$

In the preceding two examples, the double integral in Green’s theorem was easier to calculate than the line integral, so we used the theorem to calculate the line integral. In the next example, the double integral is more difficult to calculate than the line integral, so we use Green’s theorem to translate a double integral into a line integral.

Example $\PageIndex{3}$: Applying Green’s Theorem over an Ellipse

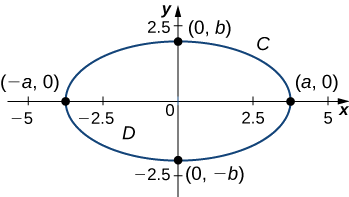
Calculate the area enclosed by ellipse $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ (Figure $\PageIndex{6}$).

Figure $\PageIndex{6}$: An ellipse defined by the equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. The boundary of the ellipse is denoted by $C$, and the region enclosed by the ellipse is labeled as $D$.

Solution

Let $C$ denote the ellipse and let $D$ be the region enclosed by $C$. Recall that ellipse $C$ can be parameterized by

• $x=a\cos t$,
• $y=b \sin t$,
• $0≤t≤2\pi$.

Calculating the area of $D$ is equivalent to computing double integral $\iint_D \,dA$. To calculate this integral without Green’s theorem, we would need to divide $D$ into two regions: the region above the x-axis and the region below. The area of the ellipse is

$$\int_{−a}^a\int_0^{\sqrt{b^2−{(bx/a)}^2}} \,dy\,dx+\int_{−a}^{a} \int_{−\sqrt{b^2−{(bx/a)}^2}}^{0} \,dy\,dx. \nonumber$$

These two integrals are not straightforward to calculate (although when we know the value of the first integral, we know the value of the second by symmetry). Instead of trying to calculate them, we use Green’s theorem to transform $\iint_D \,dA$ into a line integral around the boundary $C$.

Consider vector field

$$F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩. \nonumber$$

Then, $Q_x=\dfrac{1}{2}$ and $P_y=−\dfrac{1}{2}$, and therefore $Q_x−P_y=1$. Notice that $\mathbf F$ was chosen to have the property that $Q_x−P_y=1$. Since this is the case, Green’s theorem transforms the line integral of $\mathbf F$ over $C$ into the double integral of 1 over $D$.

By Green’s theorem,

$$\begin{align*} \iint_D \,dA &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\int_C \mathbf F\cdot d\mathbf r=\dfrac{1}{2}\int_C −y\,dx+x\,dy \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi}−b \sin t(−a\sin t)+a(\cos t)b\cos t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab \cos^2 t+ab \sin^2 t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab\,dt =\pi ab. \end{align*}$$

Therefore, the area of the ellipse is $\pi ab\;\text{units}^2$.

In Example $\PageIndex{3}$, we used vector field $\mathbf F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩$ to find the area of any ellipse. The logic of the previous example can be extended to derive a formula for the area of any region $D$. Let $D$ be any region with a boundary that is a simple closed curve $C$ oriented counterclockwise. If $F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩$, then $Q_x−P_y=1$. Therefore, by the same logic as in Example $\PageIndex{3}$,

$$\text{area of} \; D=\iint_D dA=\dfrac{1}{2}\oint_C−ydx+xdy. \label{greenarea}$$

It’s worth noting that if $F=⟨P,Q⟩$ is any vector field with $Q_x−P_y=1$, then the logic of the previous paragraph works. So. Equation $\ref{greenarea}$ is not the only equation that uses a vector field’s mixed partials to get the area of a region.

Exercise $\PageIndex{3}$

Find the area of the region enclosed by the curve with parameterization $r(t)=⟨\sin t\cos t,\sin t⟩$, $0≤t≤\pi$.

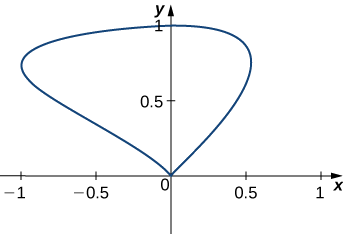
Figure $\PageIndex{7}$: A region enclosed by a curve parameterized as $\mathbf{r}(t) = \langle \sin t \cos t, \sin t \rangle$, where $0 \leq t \leq \pi$. The curve forms a closed loop.

Hint

Use Equation $\ref{greenarea}$.

Answer

$\dfrac{4}{3}$

Flux Form of Green’s Theorem

The circulation form of Green’s theorem relates a double integral over region $D$ to line integral $\oint_C \mathbf F·\mathbf Tds$, where $C$ is the boundary of $D$. The flux form of Green’s theorem relates a double integral over region $D$ to the flux across boundary $C$. The flux of a fluid across a curve can be difficult to calculate using the flux line integral. This form of Green’s theorem allows us to translate a difficult flux integral into a double integral that is often easier to calculate.

Green's Theorem (Flux Form)

Let $D$ be an open, simply connected region with a boundary curve $C$ that is a piecewise smooth, simple closed curve that is oriented counterclockwise (Figure $\PageIndex{8}$). Let $\mathbf F=⟨P,Q⟩$ be a vector field with component functions that have continuous partial derivatives on an open region containing $D$. Then,

$$\oint_C \mathbf F·\mathbf N\,ds=\iint_D P_x+Q_y\,dA. \label{GreenN}$$

Figure $\PageIndex{8}$: An open, simply connected region $D$ bounded by a curve $C$. The curve $C$ is a piecewise smooth, simple closed curve oriented counterclockwise, represented as a blue loop enclosing the shaded region $D$. Arrows labeled $N$ indicate outward-pointing unit normal vectors at various points along $C$, consistent with the counterclockwise orientation.

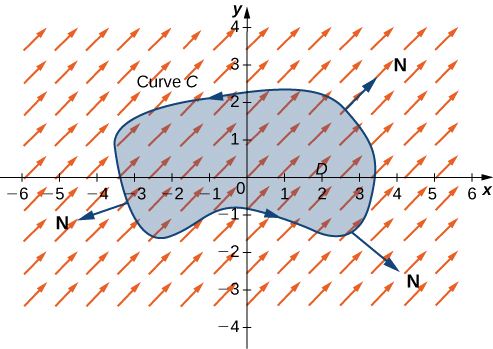
Because this form of Green’s theorem contains unit normal vector $\mathbf N$, it is sometimes referred to as the normal form of Green’s theorem.

Proof

Recall that $\displaystyle \oint_C \mathbf F·\mathbf N\,ds=\oint_C −Q\,dx+P\,dy$. Let $M=−Q$ and $N=P$. By the circulation form of Green’s theorem,

$$\begin{align*} \oint_C−Q\,dx+P\,dy &=\oint_C M\,dx+N\,dy\\[4pt] &=\iint_D N_x−M_y \,dA\\[4pt] &=\iint_D P_x−{(−Q)}_y \,dA\\[4pt] &=\iint_D P_x+Q_y \,dA. \end{align*}$$

$\square$

Example $\PageIndex{4A}$: Applying Green’s Theorem for Flux across a Circle

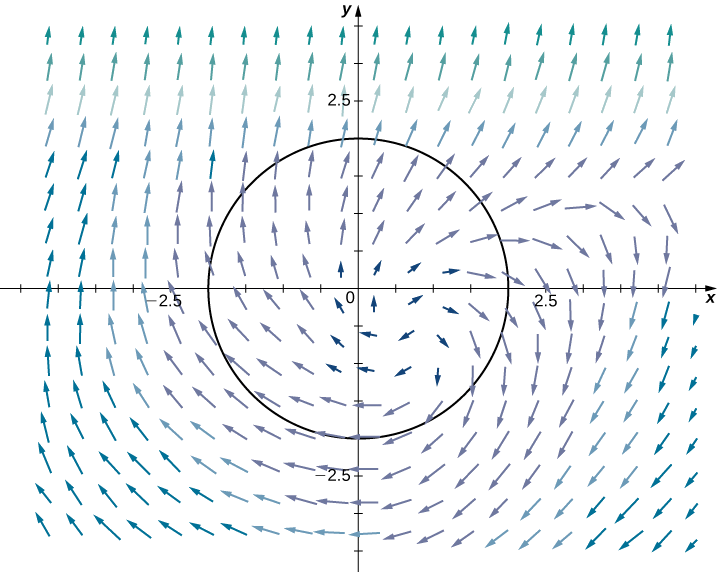
Let $C$ be a circle of radius $r$ centered at the origin (Figure $\PageIndex{9}$) and let $\mathbf F(x,y)=⟨x,y⟩$. Calculate the flux across $C$.

Figure $\PageIndex{9}$: A circle $C$ of radius $r$ centered at the origin in a two-dimensional vector field. The vector field is represented by arrows radiating outward from the origin, with their direction and magnitude indicating the components of the field at various points. The curve $C$ is shown as a black circle.

Solution

Let $D$ be the disk enclosed by $C$. The flux across $C$ is $\displaystyle \oint_C \mathbf F·\mathbf N\,ds$. We could evaluate this integral using tools we have learned, but Green’s theorem makes the calculation much more simple. Let $P(x,y)=x$ and $Q(x,y)=y$ so that $\mathbf F=⟨P,Q⟩$. Note that $P_x=1=Q_y$, and therefore $P_x+Q_y=2$. By Green’s theorem,

$$\int_C \mathbf F\cdot\mathbf N\,ds=\iint_D 2\,dA=2\iint_D \,dA. \nonumber$$

Since $\displaystyle \iint_D \,dA$ is the area of the circle, $\displaystyle \iint_D \,dA=\pi r^2$. Therefore, the flux across $C$ is $2\pi r^2$.

Example $\PageIndex{4B}$: Applying Green’s Theorem for Flux across a Triangle

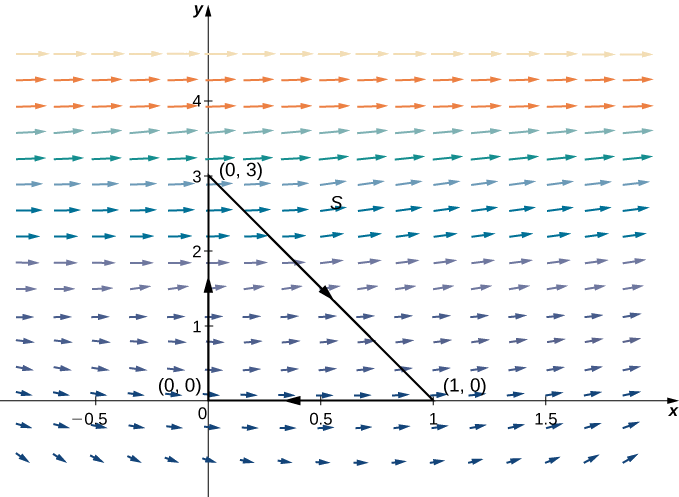
Let $S$ be the triangle with vertices $(0,0)$, $(1,0)$, and $(0,3)$ oriented clockwise (Figure $\PageIndex{10}$). Calculate the flux of $\mathbf F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2+e^y,x+y⟩$ across $S$.

Figure $\PageIndex{10}$: Curve $S$ is a triangle with vertices $(0,0)$, $(1,0)$, and $(0,3)$ oriented clockwise in a two-dimensional vector field.

Solution

To calculate the flux without Green’s theorem, we would need to break the flux integral into three line integrals, one integral for each side of the triangle. Using Green’s theorem to translate the flux line integral into a single double integral is much more simple.

Let $D$ be the region enclosed by $S$. Note that $P_x=2x$ and $Q_y=1$; therefore, $P_x+Q_y=2x+1$. Green’s theorem applies only to simple closed curves oriented counterclockwise, but we can still apply the theorem because $\displaystyle \oint_C \mathbf F·\mathbf N\,ds=−\oint_{−S} \mathbf F·\mathbf N\,ds$ and $−S$ is oriented counterclockwise. By Green’s theorem, the flux is

$$\begin{align*} \oint_C \mathbf F·\mathbf N\,ds &= \oint_{−S} \mathbf F·\mathbf N\,ds\\[4pt] &=−\iint_D (P_x+Q_y)\,dA \\[4pt] &=−\iint_D (2x+1)\,dA.\end{align*}$$

Notice that the top edge of the triangle is the line $y=−3x+3$. Therefore, in the iterated double integral, the $y$-values run from $y=0$ to $y=−3x+3$, and we have

$$\begin{align*} −\iint_D (2x+1)\,dA &= −\int_0^1\int_0^{−3x+3}(2x+1)\,dy\,dx \\[4pt] &=−\int_0^1(2x+1)(−3x+3)\,dx \\[4pt] &=−\int_0^1(−6x^2+3x+3)\,dx\\[4pt] &=−{[−2x^3+\dfrac{3x^2}{2}+3x]}_0^1 \\[4pt] &=−\dfrac{5}{2}. \end{align*}$$

Exercise $\PageIndex{4}$

Calculate the flux of $\mathbf F(x,y)=⟨x^3,y^3⟩$ across a unit circle oriented counterclockwise.

Hint

Apply Green’s theorem and use polar coordinates.

Answer

$\dfrac{3\pi}{2}$

Example $\PageIndex{5}$: Applying Green’s Theorem for Water Flow across a Rectangle

Water flows from a spring located at the origin. The velocity of the water is modeled by vector field $\mathbf v(x,y)=⟨5x+y,x+3y⟩$ m/sec. Find the amount of water per second that flows across the rectangle with vertices $(−1,−2)$, $(1,−2)$, $(1,3)$,and $(−1,3)$, oriented counterclockwise (Figure $\PageIndex{11}$).

Figure $\PageIndex{11}$: The rectangle with vertices $(−1,−2)$, $(1,−2)$, $(1,3)$,and $(−1,3)$ oriented counterclockwise.

Solution

Let $C$ represent the given rectangle and let $D$ be the rectangular region enclosed by $C$. To find the amount of water flowing across $C$, we calculate flux $\int_C \mathbf v\cdot d\mathbf r$. Let $P(x,y)=5x+y$ and $Q(x,y)=x+3y$ so that $\mathbf v=⟨P,Q⟩$. Then, $P_x=5$ and $Q_y=3$. By Green’s theorem,

$$\begin{align*} \int_C \mathbf v\cdot d\mathbf r &=\iint_D (P_x+Q_y)\,dA \\ &=\iint_D 8\,dA \\ &=8(area\space of\space D)=80. \end{align*}$$

Therefore, the water flux is 80 m²/sec.

Recall that if vector field $\mathbf F$ is conservative, then $\mathbf F$ does no work around closed curves—that is, the circulation of $\mathbf F$ around a closed curve is zero. In fact, if the domain of $\mathbf F$ is simply connected, then $\mathbf F$ is conservative if and only if the circulation of $\mathbf F$ around any closed curve is zero. If we replace “circulation of $\mathbf F$” with “flux of $\mathbf F$,” then we get a definition of a source-free vector field. The following statements are all equivalent ways of defining a source-free field $\mathbf F=⟨P,Q⟩$ on a simply connected domain (note the similarities with properties of conservative vector fields):

1. The flux $\displaystyle \oint_C \mathbf F·\mathbf N\,ds$ across any closed curve $C$ is zero.
2. If $C_1$ and $C_2$ are curves in the domain of $\mathbf F$ with the same starting points and endpoints, then $\displaystyle \int_{C_1} \mathbf F·\mathbf N\,ds=\int_{C_2} \mathbf F·\mathbf N\,ds$. In other words, flux is independent of path.
3. There is a stream function $g(x,y)$ for $\mathbf F$. A stream function for $\mathbf F=⟨P,Q⟩$ is a function g such that $P=g_y$ and $Q=−g_x$.Geometrically, $\mathbf F=\langle a,b\rangle$ is tangential to the level curve of $g$ at $(a,b)$. Since the gradient of $g$ is perpendicular to the level curve of $g$ at $(a,b)$, stream function $g$ has the property $\mathbf F(a,b)\cdot\mathbf\nabla g(a,b)=0$ for any point $(a,b)$ in the domain of $g$. (Stream functions play the same role for source-free fields that potential functions play for conservative fields.)
4. $P_x+Q_y=0$

Example $\PageIndex{6}$: Finding a Stream Function

Verify that rotation vector field $\mathbf F(x,y)=⟨y,−x⟩$ is source free, and find a stream function for $\mathbf F$.

Solution

Note that the domain of $\mathbf F$ is all of $ℝ^2$, which is simply connected. Therefore, to show that $\mathbf F$ is source free, we can show any of items 1 through 4 from the previous list to be true. In this example, we show that item 4 is true. Let $P(x,y)=y$ and $Q(x,y)=−x$. Then $P_x+0=Q_y$, and therefore $P_x+Q_y=0$. Thus, $\mathbf F$ is source free.

To find a stream function for $\mathbf F$, proceed in the same manner as finding a potential function for a conservative field. Let $g$ be a stream function for $\mathbf F$. Then $g_y=y$, which implies that

$g(x,y)=\dfrac{y^2}{2}+h(x)$.

Since $−g_x=Q=−x$, we have $h′(x)=x$. Therefore,

$h(x)=\dfrac{x^2}{2}+C$.

Letting $C=0$ gives stream function

$g(x,y)=\dfrac{x^2}{2}+\dfrac{y^2}{2}$.

To confirm that $g$ is a stream function for $\mathbf F$, note that $g_y=y=P$ and $−g_x=−x=Q$.

Notice that source-free rotation vector field $\mathbf F(x,y)=⟨y,−x⟩$ is perpendicular to conservative radial vector field $\mathbf \nabla g=⟨x,y⟩$ (Figure $\PageIndex{12}$).

Figure $\PageIndex{12}$: (a) The three-level curves of $g$ and vector field $\mathbf F$. Note that the $\mathbf F$ vectors on a given level curve are tangent to the level curve. (b) The three-level curves of $g$ and vector field $\mathbf\nabla g$. The gradient vectors are perpendicular to the corresponding level curve. Therefore, $\mathbf F(a,b)\cdot\mathbf\nabla g(a,b)=0$ for any point in the domain of $g$.

Exercise $\PageIndex{6}$

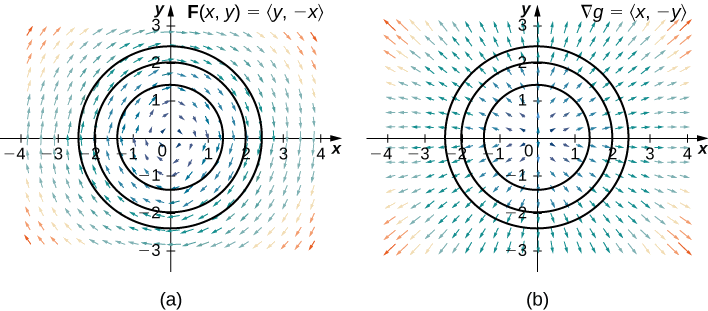
Find a stream function for vector field $\mathbf F(x,y)=⟨x \sin y,\cos y⟩$.

Hint

Follow the outline provided in the previous example.

Answer

$g(x,y)=−x\cos y$

Vector fields that are both conservative and source free are important vector fields. One important feature of conservative and source-free vector fields on a simply connected domain is that any potential function $f$ of such a field satisfies Laplace’s equation $f_{xx}+f_{yy}=0$. Laplace’s equation is foundational in the field of partial differential equations because it models such phenomena as gravitational and magnetic potentials in space, and the velocity potential of an ideal fluid. A function that satisfies Laplace’s equation is called a harmonic function. Therefore any potential function of a conservative and source-free vector field is harmonic.

To see that any potential function of a conservative and source-free vector field on a simply connected domain is harmonic, let $f$ be such a potential function of vector field $\mathbf F=⟨P,Q⟩$. Then, $f_x=P$ and $f_x=Q$ because $\mathbf \nabla f=\mathbf F$. Therefore, $f_{xx}=P_x$ and $f_{yy}=Q_y$. Since $\mathbf F$ is source free, $f_{xx}+f_{yy}=P_x+Q_y=0$, and we have that $f$ is harmonic.

Example $\PageIndex{7}$: Satisfying Laplace’s Equation

For vector field $\mathbf F(x,y)=⟨e^x\sin y,e^x\cos y⟩$, verify that the field is both conservative and source free, find a potential function for $\mathbf F$, and verify that the potential function is harmonic.

Solution

Let $P(x,y)=e^x\sin y$ and $Q(x,y)=e^x \cos y$. Notice that the domain of $\mathbf F$ is all of two-space, which is simply connected. Therefore, we can check the cross-partials of $\mathbf F$ to determine whether $\mathbf F$ is conservative. Note that $P_y=e^x \cos y=Q_x$, so $\mathbf F$ is conservative. Since $P_x=e^x \sin y$ and $Q_y=e^x \sin y$, $P_x+Q_y=0$ and the field is source free.

To find a potential function for $\mathbf F$, let $f$ be a potential function. Then, $\mathbf \nabla f=\mathbf F$, so $f_x(x,y)=e^x \sin y$. Integrating this equation with respect to x gives $f(x,y)=e^x \sin y+h(y)$. Since $f_y(x,y)=e^x \cos y$, differentiating $f$ with respect to y gives $e^x\cos y=e^x\cos y+h′(y)$. Therefore, we can take $h(y)=0$, and $f(x,y)=e^x\sin y$ is a potential function for $f$.

To verify that $f$ is a harmonic function, note that $f_{xx}(x,y)=\dfrac{\partial}{\partial x}(e^x\sin y)=e^x \sin y$ and

$f_{yy}(x,y)=\dfrac{\partial}{\partial x}(e^x\cos y)=−e^x\sin y$. Therefore, $f_{xx}+f_{yy}=0$, and $f$ satisfies Laplace’s equation.

Exercise $\PageIndex{7}$

Is the function $f(x,y)=e^{x+5y}$ harmonic?

Hint

Determine whether the function satisfies Laplace’s equation.

Answer

No

Green’s Theorem on General Regions

Green’s theorem, as stated, applies only to regions that are simply connected—that is, Green’s theorem as stated so far cannot handle regions with holes. Here, we extend Green’s theorem so that it does work on regions with finitely many holes (Figure $\PageIndex{13}$).

Figure $\PageIndex{13}$: A nonsimply connected region with three holes. Green’s theorem, as stated, does not apply to a nonsimply connected region with three holes like this one.

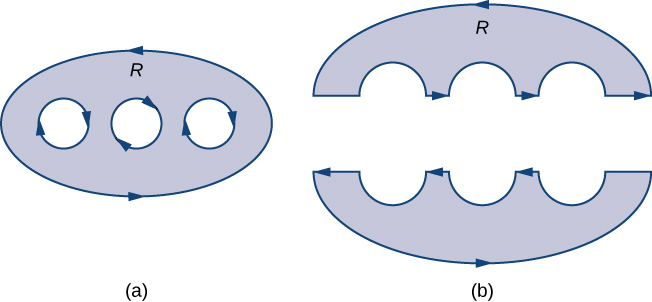
Before discussing extensions of Green’s theorem, we need to go over some terminology regarding the boundary of a region. Let $D$ be a region and let $C$ be a component of the boundary of $D$. We say that $C$ is positively oriented if, as we walk along $C$ in the direction of orientation, region $D$ is always on our left. Therefore, the counterclockwise orientation of the boundary of a disk is a positive orientation, for example. Curve $C$ is negatively oriented if, as we walk along $C$ in the direction of orientation, region $D$ is always on our right. The clockwise orientation of the boundary of a disk is a negative orientation, for example.

Let $D$ be a region with finitely many holes (so that $D$ has finitely many boundary curves), and denote the boundary of $D$ by $\partial D$ (Figure $\PageIndex{14}$). To extend Green’s theorem so it can handle $D$, we divide region $D$ into two regions, $D_1$ and $D_2$ (with respective boundaries $\partial D_1$ and $\partial D_2$), in such a way that $D=D_1\cup D_2$ and neither $D_1$ nor $D_2$ has any holes (Figure $\PageIndex{14}$).

Figure $\PageIndex{14}$: In part (a), the region $D$ is shown as a shaded area with an outer boundary labeled $R$ and three internal holes, each with their own oriented boundary. In part (b), the same region is divided into two subregions, which are shaded separately. These subregions are constructed such that neither contains any holes, making them simply connected regions.

Assume the boundary of $D$ is oriented as in the figure, with the inner holes given a negative orientation and the outer boundary given a positive orientation. The boundary of each simply connected region $D_1$ and $D_2$ is positively oriented. If $\mathbf F$ is a vector field defined on $D$, then Green’s theorem says that

$$\begin{align} \oint_{\partial D} \mathbf F·d\mathbf{r} &=\oint_{\partial D_1}\mathbf F·d\mathbf{r}+\oint_{\partial D_2}\mathbf F·d\mathbf{r} \\ &=\iint_{D_1}Q_x−P_y\,dA+\iint_{D_2}Q_x−P_y\,dA \\ &=\iint_D (Q_x−P_y)\,dA.\end{align}$$

Therefore, Green’s theorem still works on a region with holes.

To see how this works in practice, consider annulus $D$ in Figure $\PageIndex{15}$ and suppose that $F=⟨P,Q⟩$ is a vector field defined on this annulus. Region $D$ has a hole, so it is not simply connected. Orient the outer circle of the annulus counterclockwise and the inner circle clockwise (Figure $\PageIndex{15}$) so that, when we divide the region into $D_1$ and $D_2$, we are able to keep the region on our left as we walk along a path that traverses the boundary. Let $D_1$ be the upper half of the annulus and $D_2$ be the lower half. Neither of these regions has holes, so we have divided $D$ into two simply connected regions.

We label each piece of these new boundaries as $P_i$ for some $i$, as in Figure $\PageIndex{15}$. If we begin at $P$ and travel along the oriented boundary, the first segment is $P_1$, then $P_2$, $P_3$, and $P_4$. Now we have traversed $D_1$ and returned to $P$. Next, we start at $P$ again and traverse $D_2$. Since the first piece of the boundary is the same as $P_4$ in $D_1$, but oriented in the opposite direction, the first piece of $D_2$ is $−P_4$. Next, we have $P_5$, then $−P_2$, and finally $P_6$.

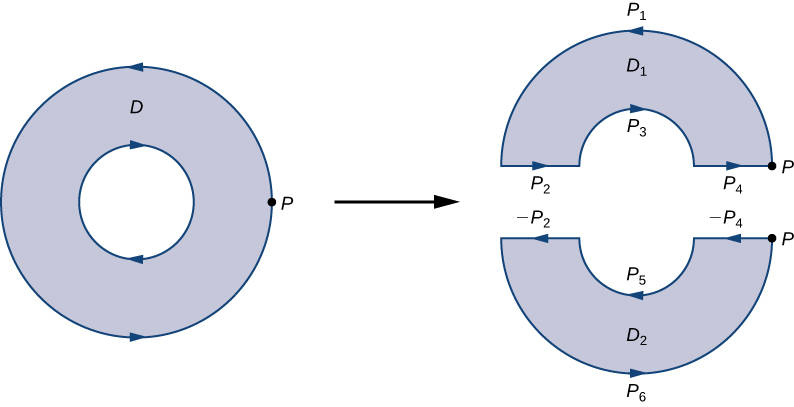
Figure $\PageIndex{15}$: On the left side is the region $D$ is shown as an annulus with a single hole and an oriented boundary. The outer boundary is oriented counterclockwise, while the inner boundary is oriented clockwise. The arrow pointing from the left image to the right image show how an annular region $D$ with a hole can be split into two simply connected regions $D_1$ and $D_2$ for the application of Green's Theorem. On the right side is the annular region $D$ is divided into two subregions, $D_1$ and $D_2$, with their respective boundaries labeled $P_1$, $P_2$, $P_3$, $P_4$, $P_5$, and $P_6$. The orientation of the boundaries is preserved, and the common boundaries between $D_1$ and $D_2$ have opposite orientations.

Figure $\PageIndex{15}$ shows a path that traverses the boundary of $D$. Notice that this path traverses the boundary of region $D_1$, returns to the starting point, and then traverses the boundary of region $D_2$. Furthermore, as we walk along the path, the region is always on our left. Notice that this traversal of the $P_i$ paths covers the entire boundary of region $D$. If we had only traversed one portion of the boundary of $D$, then we cannot apply Green’s theorem to $D$.

The boundary of the upper half of the annulus, therefore, is $P_1\cup P_2\cup P_3\cup P_4$ and the boundary of the lower half of the annulus is $−P_4\cup P_5\cup −P_2\cup P_6$. Then, Green’s theorem implies

$$\begin{align} \oint_{\partial D}\mathbf F·d\mathbf{r} &=\int_{P_1}\mathbf F·d\mathbf{r}+\int_{P_2}\mathbf F·d\mathbf{r}+\int_{P_3}\mathbf F·d\mathbf{r}+\int_{P_4}\mathbf F·d\mathbf{r}+\int_{−P_4}\mathbf F·d\mathbf{r}+\int_{P_5}\mathbf F·d\mathbf{r}+\int_{−P_2}\mathbf F·d\mathbf{r}+\int_{P_6}\mathbf F·d\mathbf{r} \\ &=\int_{P_1}\mathbf F·d\mathbf{r}+\int_{P_2}\mathbf F·d\mathbf{r}+\int_{P_3}\mathbf F·d\mathbf{r}+\int_{P_4}\mathbf F·d\mathbf{r}+\int_{P_4}\mathbf F·d\mathbf{r}+\int_{P_5}\mathbf F·d\mathbf{r}+\int_{−P_2}\mathbf F·d\mathbf{r}+\int_{P_6}\mathbf F·d\mathbf{r} \\ &=\int_{P_1}\mathbf F·d\mathbf{r}+\int_{P_3}\mathbf F·d\mathbf{r}+\int_{P_5}\mathbf F·d\mathbf{r}+\int_{P_6}\mathbf F·d\mathbf{r} \\ &=\oint_{\partial D_1}\mathbf F·d\mathbf{r}+\oint_{\partial D_2}\mathbf F·d\mathbf{r}\\ &=\iint_{D_1}(Q_x−P_y)\,dA+\iint_{D_2}(Q_x−P_y)\,dA \\ &=\iint_D(Q_x−P_y)\,dA. \end{align}$$

Therefore, we arrive at the equation found in Green’s theorem—namely,

$$\oint_{\partial D}\mathbf F·d\mathbf{r}=\iint_D (Q_x−P_y)\,dA.$$

The same logic implies that the flux form of Green’s theorem can also be extended to a region with finitely many holes:

$$\oint_C F·N\,ds=\iint_D (P_x+Q_y)\,dA.$$

Example $\PageIndex{8A}$: ​​​​​​Using Green’s Theorem on a Region with Holes

Calculate the integral

$$\oint_{\partial D}(\sin x−\dfrac{y^3}{3})dx+(\dfrac{y^3}{3}+\sin y)dy,$$

where $D$ is the annulus given by the polar inequalities $1≤r≤2$, $0≤\theta≤2\pi$.

Solution

Although $D$ is not simply connected, we can use the extended form of Green’s theorem to calculate the integral. Since the integration occurs over an annulus, we convert to polar coordinates:

$$\begin{align*} \oint_{\partial D}(\sin x−\dfrac{y^3}{3})\,dx+(\dfrac{x^3}{3}+\sin y)\,dy &=\iint_D (Q_x−P_y)\,dA \\ &=\iint_D (x^2+y^2)\,dA\\ &=\int_0^{2\pi}\int_1^2 r^3\,drd\theta=\int_0^{2\pi} \dfrac{15}{4}\,d\theta \\ &=\dfrac{15\pi}{2}. \end{align*}$$

Example $\PageIndex{8B}$: Using the Extended Form of Green’s Theorem

Let $\mathbf F=⟨P,Q⟩=⟨\dfrac{y}{x^2+y^2},-\dfrac{x}{x^2+y^2}⟩$ and let $C$ be any simple closed curve in a plane oriented counterclockwise. What are the possible values of $\oint_C \mathbf F·d\mathbf{r}$?

Solution

We use the extended form of Green’s theorem to show that $\oint_C \mathbf F·d\mathbf{r}$ is either $0$ or $−2\pi$—that is, no matter how crazy curve $C$ is, the line integral of $\mathbf F$ along $C$ can have only one of two possible values. We consider two cases: the case when $C$ encompasses the origin and the case when $C$ does not encompass the origin.

Case 1: C Does Not Encompass the Origin

In this case, the region enclosed by $C$ is simply connected because the only hole in the domain of $\mathbf F$ is at the origin. We showed in our discussion of cross-partials that $\mathbf F$ satisfies the cross-partial condition. If we restrict the domain of $\mathbf F$ just to $C$ and the region it encloses, then $\mathbf F$ with this restricted domain is now defined on a simply connected domain. Since $\mathbf F$ satisfies the cross-partial property on its restricted domain, the field $\mathbf F$ is conservative on this simply connected region and hence the circulation $\oint_C \mathbf F·d\mathbf{r}$ is zero.

Case 2: C Does Encompass the Origin

In this case, the region enclosed by $C$ is not simply connected because this region contains a hole at the origin. Let $C_1$ be a circle of radius a centered at the origin so that $C_1$ is entirely inside the region enclosed by $C$ (Figure $\PageIndex{16}$). Give $C_1$ a clockwise orientation.

Figure $\PageIndex{16}$: A region enclosed by a closed curve $C$ that is not simply connected because it contains a hole at the origin. The outer boundary, $C$, is a smooth, simple closed curve with a counterclockwise orientation. Inside $C$, there is a smaller circular boundary $C_1$, which is centered at the origin and oriented clockwise.

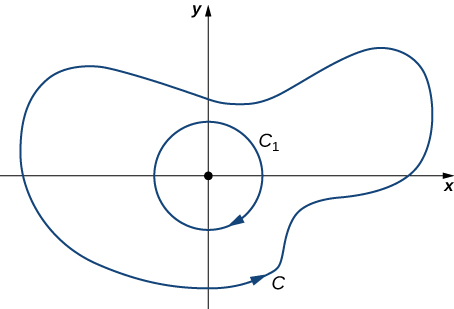
Let $D$ be the region between $C_1$ and $C$, and $C$ is orientated counterclockwise. By the extended version of Green’s theorem,

$$\begin{align*} \int_C \mathbf F·d\mathbf{r}+\int_{C_1}\mathbf F·d\mathbf{r} &=\iint_D Qx_−P_y \,dA \\[4pt] &=\iint_D−\dfrac{y^2−x^2}{{(x^2+y^2)}^2}+\dfrac{y^2−x^2}{{(x^2+y^2)}^2}dA \\[4pt] &=0, \end{align*}$$

and therefore

$$\int_C \mathbf F·d\mathbf{r}=−\int_{C_1} \mathbf F·d\mathbf{r}. \nonumber$$

Since $C_1$ is a specific curve, we can evaluate $\int_{C_1}\mathbf F·d\mathbf{r}$. Let

$$x=a\cos t, \;\; y=a\sin t, \;\; 0≤t≤2\pi \nonumber$$

be a parameterization of $C_1$. Then,

$$\begin{align*} \int_{C_1}\mathbf F·d\mathbf{r} &=\int_0^{2\pi} F(r(t))·r′(t)dt \\[4pt] &=\int_0^{2\pi} ⟨−\dfrac{\sin(t)}{a},−\dfrac{\cos(t)}{a}⟩·⟨−a\sin(t),−a\cos(t)⟩dt \\[4pt] &=\int_0^{2\pi}{\sin}^2(t)+{\cos}^2(t)dt \\[4pt] &=\int_0^{2\pi}dt=2\pi. \end{align*}$$

Therefore, $\int_C F·ds=−2\pi$.

Exercise $\PageIndex{8}$

Calculate integral $\oint_{\partial D}\mathbf F·d\mathbf{r}$, where $D$ is the annulus given by the polar inequalities $2≤r≤5$, $0≤\theta≤2\pi$, and $F(x,y)=⟨x^3,5x+e^y\sin y⟩$.

Hint

Use the extended version of Green’s theorem.

Answer

$105\pi$

Measuring Area From A Boundary: The Planimeter

Imagine you are a doctor who has just received a magnetic resonance image of your patient’s brain. The brain has a tumor (Figure $\PageIndex{17}$). How large is the tumor? To be precise, what is the area of the red region? The red cross-section of the tumor has an irregular shape, and therefore it is unlikely that you would be able to find a set of equations or inequalities for the region and then be able to calculate its area by conventional means. You could approximate the area by chopping the region into tiny squares (a Riemann sum approach), but this method always gives an answer with some error.

Figure $\PageIndex{17}$: This magnetic resonance image of a patient’s brain shows a tumor, which is highlighted in red. ( CC-BY-2.0 modification of work by oatsy40, Wikipedia)

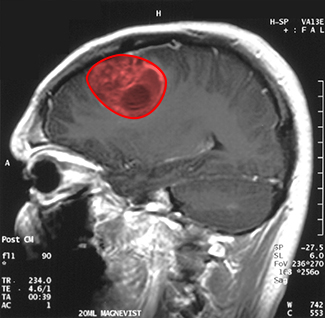
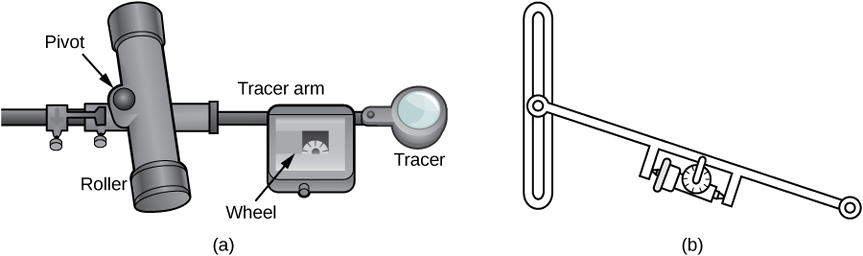
Instead of trying to measure the area of the region directly, we can use a device called a rolling planimeter to calculate the area of the region exactly, simply by measuring its boundary. In this project you investigate how a planimeter works, and you use Green’s theorem to show the device calculates area correctly.

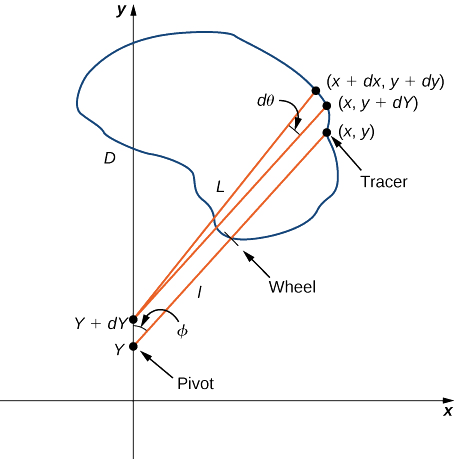
A rolling planimeter is a device that measures the area of a planar region by tracing out the boundary of that region (Figure $\PageIndex{18}$). To measure the area of a region, we simply run the tracer of the planimeter around the boundary of the region. The planimeter measures the number of turns through which the wheel rotates as we trace the boundary; the area of the shape is proportional to this number of wheel turns. We can derive the precise proportionality equation using Green’s theorem. As the tracer moves around the boundary of the region, the tracer arm rotates and the roller moves back and forth (but does not rotate).

Figure $\PageIndex{18}$: (a) A rolling planimeter. The pivot allows the tracer arm to rotate. The roller itself does not rotate; it only moves back and forth. (b) An interior view of a rolling planimeter. Notice that the wheel cannot turn if the planimeter is moving back and forth with the tracer arm perpendicular to the roller.

Let $C$ denote the boundary of region $D$, the area to be calculated. As the tracer traverses curve $C$, assume the roller moves along the y-axis (since the roller does not rotate, one can assume it moves along a straight line). Use the coordinates $(x,y)$ to represent points on boundary $C$, and coordinates $(0,Y)$ to represent the position of the pivot. As the planimeter traces $C$, the pivot moves along the y-axis while the tracer arm rotates on the pivot.

Begin the analysis by considering the motion of the tracer as it moves from point $(x,y)$ counterclockwise to point $(x+dx,y+dy)$ that is close to $(x,y)$ (Figure $\PageIndex{19}$). The pivot also moves, from point $(0,Y)$ to nearby point $(0,Y+dY)$. How much does the wheel turn as a result of this motion? To answer this question, break the motion into two parts. First, roll the pivot along the y-axis from $(0,Y)$ to $(0,Y+dY)$ without rotating the tracer arm. The tracer arm then ends up at point $(x,y+dY)$ while maintaining a constant angle $\phi$ with the x-axis. Second, rotate the tracer arm by an angle $d\theta$ without moving the roller. Now the tracer is at point $(x+dx,y+dy)$. Let ll be the distance from the pivot to the wheel and let L be the distance from the pivot to the tracer (the length of the tracer arm).

Figure $\PageIndex{19}$: A mathematical analysis of the motion of a planimeter. The region $D$ is bounded by a closed curve $C$, shown in blue. The planimeter's components are labeled as the "Tracer," "Wheel," and "Pivot," with the tracer point moving along the curve $C$. At any given moment, the tracer is at position $(x, y)$, and its displacement is represented as $(x + dx, y + dy)$.

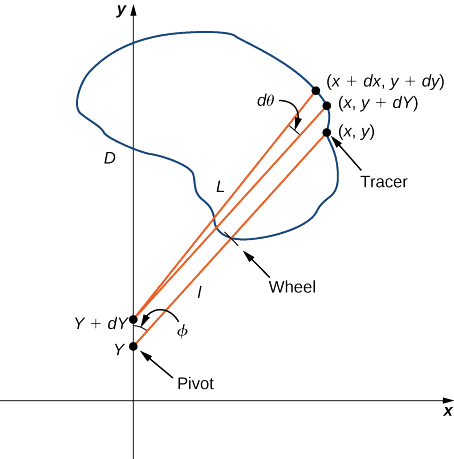
1. Explain why the total distance through which the wheel rolls the small motion just described is $\sin \phi dY+ld\theta=\dfrac{x}{L}dY+ld\theta$.
2. Show that $\oint_C d\theta=0$.
3. Use step 2 to show that the total rolling distance of the wheel as the tracer traverses curve $C$ is
   Total wheel roll $=\dfrac{1}{L}\oint_C xdY$.
   Now that you have an equation for the total rolling distance of the wheel, connect this equation to Green’s theorem to calculate area $D$ enclosed by $C$.
4. Show that $x^2+(y−Y)^2=L^2$.
5. Assume the orientation of the planimeter is as shown in Figure $\PageIndex{18}$. Explain why $Y≤y$, and use this inequality to show there is a unique value of $Y$ for each point $(x,y)$: $Y=y=\sqrt{L^2−x^2}$.
6. Use step 5 to show that $dY=dy+\dfrac{x}{L^2−x^2}dx.$
7. Use Green’s theorem to show that $\displaystyle \oint_C \dfrac{x}{L^2−x^2}dx=0$.
8. Use step 7 to show that the total wheel roll is

   $$\text{Total wheel roll}\quad =\quad 1L\oint_C x\,dy.$$

   It took a bit of work, but this equation says that the variable of integration Y in step 3 can be replaced with y.

9. Use Green’s theorem to show that the area of $D$ is $\oint_C xdy$. The logic is similar to the logic used to show that the area of $\displaystyle D=12\oint_C −y\,dx+x\,dy$.
10. Conclude that the area of $D$ equals the length of the tracer arm multiplied by the total rolling distance of the wheel.

You now know how a planimeter works and you have used Green’s theorem to justify that it works. To calculate the area of a planar region $D$, use a planimeter to trace the boundary of the region. The area of the region is the length of the tracer arm multiplied by the distance the wheel rolled.

Key Concepts

• Green’s theorem relates the integral over a connected region to an integral over the boundary of the region. Green’s theorem is a version of the Fundamental Theorem of Calculus in one higher dimension.
• Green’s Theorem comes in two forms: a circulation form and a flux form. In the circulation form, the integrand is $\mathbf F·\mathbf T$. In the flux form, the integrand is $\mathbf F·\mathbf N$.
• Green’s theorem can be used to transform a difficult line integral into an easier double integral, or to transform a difficult double integral into an easier line integral.
• A vector field is source free if it has a stream function. The flux of a source-free vector field across a closed curve is zero, just as the circulation of a conservative vector field across a closed curve is zero.

Key Equations

• Green’s theorem, circulation form
  $\displaystyle ∮_C P\,dx+Q\,dy=∬_D Q_x−P_y\,dA$, where $C$ is the boundary of $D$
• Green’s theorem, flux form
  $\displaystyle ∮_C\mathbf F·\mathbf N\,ds=∬_D P_x+Q_y\,dA$, where $C$ is the boundary of $D$
• Green’s theorem, extended version
  $\displaystyle ∮_{\partial D}\mathbf F·d\mathbf{r}=∬_D Q_x−P_y\,dA$

Glossary

Green’s theorem

relates the integral over a connected region to an integral over the boundary of the region

Stream function

if $\mathbf F=⟨P,Q⟩$ is a source-free vector field, then stream function $g$ is a function such that $P=g_y$ and $Q=−g_x$

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.