The Product and Quotient Rules
- Page ID
- 626
Theorem: The Product Rule
Let \(f\) and \(g\) be differentiable functions. Then
\[ \left[f(x) \, g(x)\right] ' = f(x)\, g '(x) + f '(x) \,g(x) \]
Proof
We have
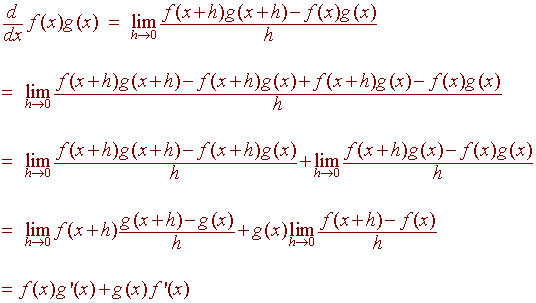
Example \(\PageIndex{1}\)
Find
\[\dfrac{d}{dx } (2 - x^2)(x^4 - 5) \nonumber\]
Solution:
Here
\[ f(x) = 2 - x^2 \nonumber\]
and
\[ g(x) = x^4 - 5 \nonumber\]
The product rule gives
\[\dfrac{d}{dx } (2 - x^2)(x^4 - 5) = (2 - x^2)(4x^3) + (-2x)(x^4 - 5) \nonumber\]
The Quotient Rule
Remember the poem
"lo d hi minus hi d lo square the bottom and away you go"
This poem is the mnemonic for the taking the derivative of a quotient.
Theorem: The Quotient Rule
Let f and g be differentiable functions. Then
\[ \dfrac{d}{dx} \dfrac{f(x)}{g(x)} = \dfrac{g(x)\, f'(x) - f(x) \, g'(x)}{g(x)^2} \label{quot} \]
Example \(\PageIndex{2}\):
Find \(y'\) if
\[ y' =\dfrac{2x - 1}{x + 1} \nonumber\]
Solution
Here
\[ f(x) = 2x - 1 \nonumber\]
and
\[ g(x) = x + 1 \nonumber\]
The quotient rule (Equation \ref{quot}) gives
\[\begin{align*} \dfrac{ (x + 1)(2) - (2x - 1)(1)}{ (x + 1)2} &= \dfrac{2x + 2 - 2x + 1}{(x + 1)2} \\[4pt] &= \dfrac{3}{ (x + 1)2} \end{align*}\]


