2.3: Tangent Plane to a Surface
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the previous section we mentioned that the partial derivatives ∂f∂x and ∂f∂y can be thought of as the rate of change of a function z=f(x,y) in the positive x and y directions, respectively. Recall that the derivative dydx of a function y=f(x) has a geometric meaning, namely as the slope of the tangent line to the graph of f at the point (x,f(x)) in R2. There is a similar geometric meaning to the partial derivatives ∂f∂x and ∂f∂y of a function z=f(x,y): given a point (a,b) in the domain D of f(x,y), the trace of the surface described by z=f(x,y) in the plane y=b is a curve in R3 through the point (a,b,f(a,b)), and the slope of the tangent line Lx to that curve at that point is ∂f∂x(a,b). Similarly, ∂f∂y(a,b) is the slope of the tangent line Ly to the trace of the surface z=f(x,y) in the plane x=a (see Figure 2.3.1).

Since the derivative dydx of a function y=f(x) is used to find the tangent line to the graph of f (which is a curve in R2), you might expect that partial derivatives can be used to define a tangent plane to the graph of a surface z=f(x,y). This indeed turns out to be the case. First, we need a definition of a tangent plane. The intuitive idea is that a tangent plane “just touches” a surface at a point. The formal definition mimics the intuitive notion of a tangent line to a curve.
Definition 2.4: Tangent Planes
Let z=f(x,y) be the equation of a surface S in R3, and let P=(a,b,c) be a point on S. Let T be a plane which contains the point P, and let Q=(x,y,z) represent a generic point on the surface S. If the (acute) angle between the vector →PQ and the plane T approaches zero as the point Q approaches P along the surface S, then we call T the tangent plane to S at P.
Note that since two lines in R3 determine a plane, then the two tangent lines to the surface z=f(x,y) in the x and y directions described in Figure 2.3.1 are contained in the tangent plane at that point, if the tangent plane exists at that point. The existence of those two tangent lines does not by itself guarantee the existence of the tangent plane. It is possible that if we take the trace of the surface in the plane x−y=0 (which makes a 45◦ angle with the positive x-axis), the resulting curve in that plane may have a tangent line which is not in the plane determined by the other two tangent lines, or it may not have a tangent line at all at that point. Luckily, it turns out that if ∂f∂x and ∂f∂y exist in a region around a point (a,b) and are continuous at (a,b) then the tangent plane to the surface z=f(x,y) will exist at the point (a,b,f(a,b)). In this text, those conditions will always hold.
Suppose that we want an equation of the tangent plane T to the surface z=f(x,y) at a point (a,b,f(a,b)). Let Lx and Ly be the tangent lines to the traces of the surface in the planes y=b and x=a, respectively (as in Figure 2.3.2), and suppose that the conditions for T to exist do hold. Then the equation for T is
A(x−a)+B(y−b)+C(z−f(a,b))=0
where n=(A,B,C) is a normal vector to the plane T. Since T contains the lines Lx and Ly, then all we need are vectors vx and vy that are parallel to Lxand Ly, respectively, and then let n=vx×vy.

Since the slope of Lx is ∂f∂x(a,b), then the vector vx=(1,0,∂f∂x(a,b)) is parallel to Lx (since vx lies in the xz-plane and lies in a line with slope ∂f∂x(a,b)1=∂f∂x(a,b). See Figure 2.3.3). Similarly, the vector vy=(0,1,∂f∂y(a,b)) is parallel to Ly. Hence, the vector
n=vx×vy=|ijk10∂f∂x(a,b)01∂f∂y(a,b)|=−∂f∂x(a,b)i−∂f∂y(a,b)j+k
is normal to the plant T. Thus the equation of T is
−∂f∂x(a,b)(x−a)−∂f∂y(a,b)(y−b)+z−f(a,b)=0
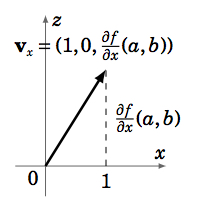
Multiplying both sides by −1, we have the following result:
The equation of the tangent plane to the surface z=f(x,y) at the point (a,b,f(a,b)) is
∂f∂x(a,b)(x−a)+∂f∂y(a,b)(y−b)−z+f(a,b)=0
Example 2.13
Find the equation of the tangent plane to the surface z=x2+y2 at the point (1,2,5).
Solution
For the function f(x,y)=x2+y2, we have ∂f∂x=2x and ∂f∂y=2y, so the equation of the tangent plane at the point (1,2,5) is
2(1)(x−1)+2(2)(y−2)−z+5=0 , or
2x+4y−z−5=0
In a similar fashion, it can be shown that if a surface is defined implicitly by an equation of the form F(x,y,z)=0, then the tangent plane to the surface at a point (a,b,c) is given by the equation
∂F∂x(a,b,c)(x−a)+∂F∂y(a,b,c)(y−b)+∂F∂z(a,b,c)(z−c)=0
Note that Equation ??? is the special case of Equation ??? where F(x,y,z)=f(x,y)−z.
Example 2.14
Find the equation of the tangent plane to the surface x2+y2+z2=9 at the point (2,2,−1).
For the function F(x,y,z)=x2+y2+z2−9, we have ∂F∂x=2x, ∂F∂y=2y, and ∂F∂z=2z, so the equation of the tangent plane at (2,2,−1) is
2(2)(x−2)+2(2)(y−2)+2(−1)(z+1)=0, or
2x+2y−z−9=0



