4.2: Product Groups

So far, we have a fairly small collection of examples of groups: the dihedral groups, the symmetric group, and $\mathbb{Z}_n$. In this section, we'll look at products of groups and find a way to make new groups from the groups we already know.

A very famous group - though not a very complicated one - is the Klein Four-Group. This is the symmetry group of a rectangle. It has a pair of generators, given by the flips over the horizontal and vertical axes.

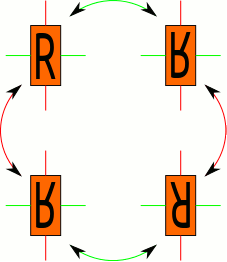
Figure 4.2.1. The symmetries of a rectangle, given by the Klien 4-group.

But the Klein Four-Group can also be thought of as a kind of mash-up of two copies of $\mathbb{Z}_2$. Let $H$ be the additive group with elements $\{(0,0), (1,0), (0,1), (1,1)\}$, and operation given by just adding the elements coordinate-wise as elements of $\mathbb{Z}_2$. (So that $(1,0)+(1,1)=(0,1)$. Then $H$ is a group (check!), and is in fact isomorphic to the Klein Four-Group. It's an example of a product group!

Let's be more precise and set a definition of a product group.

Definition 4.1.0: Direct Product

The direct product (or just product) of two groups $G$ and $H$ is the group $G\times H$ with elements $(g,h)$ where $g\in G$ and $h\in H$. The group operation is given by $(g_1, h_1)\cdot (g_2, h_2) = (g_1g_2, h_1h_2)$, where the coordinate-wise operations are the operations in $G$ and $H$.

Here's an example. Take $G=\mathbb{Z}_3$ and $H=\mathbb{Z}_6$, and consider the product $G\times H$. The product group has 18 elements: there are three choices for the first coordinate and 6 choices for the second coordinate. Since we use addition as the operation in both of the coordinate groups, we'll use addition as the operation in the product. So consider elements $(2,4)$ and $(1,3)$. Then $(2,4)+(1,3)=(0,1)$; addition in the first coordinate is according to $\mathbb{Z}_3$, and addition in the second coordinate is according to $\mathbb{Z}_6$.

We should check that the product of any pair of groups $G$ and $H$ is actually a group.

1. The product group has an identity $(1,1)$: $(1,1)\cdot (g,h)=(1g,1h)=(g,h)$.
2. Associativity follows from associativity of $G$ and $H$.
3. Closure also follows from closure in $G$ and $H$.
4. The inverse of $(g,h)$ is $(g^{-1},h^{-1})$.

So $G\times H$ really is a group.

We saw in the example that $\mathbb{Z}_3 \times \mathbb{Z}_6$ has 18 elements. This isn't a coincidence! For any finite groups $G$ and $H$, the product group has $|G||H|$ elements.

An interesting question at this point is suggested by Lagrange's Theorem, which told us that the cardinality of any subgroup divides the cardinality of the original group. We've seen that we can form product group sto 'multiply' groups: Is it also possible to 'divide' groups? Over the next few sections, we'll develop ideas that will let us build quotient groups.

Not all product groups are commutative. How many elements are in $G=S_4\times \mathbb{Z}_3$? Identify the identity. Write down a few non-identity elements and compute their respective products.

Contributors and Attributions

• Tom Denton (Fields Institute/York University in Toronto)