5.1: Roots and Radicals
- Page ID
- 6261
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Identify and evaluate square and cube roots.
- Determine the domain of functions involving square and cube roots.
- Evaluate \(n\)th roots.
- Simplify radicals using the product and quotient rules for radicals.
Square and Cube Roots
Recall that a square root1 of a number is a number that when multiplied by itself yields the original number. For example, \(5\) is a square root of \(25\), because \(5^{2} = 25\). Since \((−5)^{2} = 25\), we can say that \(−5\) is a square root of \(25\) as well. Every positive real number has two square roots, one positive and one negative. For this reason, we use the radical sign \(√\) to denote the principal (nonnegative) square root2 and a negative sign in front of the radical \(−√\) to denote the negative square root.
\(\begin{aligned} \sqrt { 25 } & = 5 \quad\quad\color{Cerulean} { Positive\: square \:root \:of \: 25} \\ - \sqrt { 25 } & = - 5 \quad\:\color{Cerulean} { Negative \:square\: root \:of\: 25} \end{aligned}\)
Zero is the only real number with one square root.
\(\sqrt { 0 } = 0 \text { because } 0 ^ { 2 } = 0\)
Example \(\PageIndex{1}\):
Evaluate.
- \(\sqrt { 121 }\)
- \(- \sqrt { 81 }\)
Solution
- \(\sqrt { 121 } = \sqrt { 11 ^ { 2 } } = 11\)
- \(- \sqrt { 81 } = - \sqrt { 9 ^ { 2 } } = - 9\)
If the radicand3, the number inside the radical sign, can be factored as the square of another number, then the square root of the number is apparent. In this case, we have the following property:
\(\sqrt { a ^ { 2 } } = a \quad \text { if } \quad a \geq 0\)
Or more generally,
\(\sqrt { a ^ { 2 } } = | a | \quad \text { if } \quad a \in R\)
The absolute value is important because \(a\) may be a negative number and the radical sign denotes the principal square root. For example,
\(\sqrt { ( - 8 ) ^ { 2 } } = | -8| = 8\)
Make use of the absolute value to ensure a positive result.
Example \(\PageIndex{2}\):
Simplify: \(\sqrt { ( x - 2 ) ^ { 2 } }\).
Solution
Here the variable expression \(x − 2\) could be negative, zero, or positive. Since the sign depends on the unknown quantity \(x\), we must ensure that we obtain the principal square root by making use of the absolute value.
\(\sqrt { ( x - 2 ) ^ { 2 } } = | x - 2 |\)
Answer:
\(| x - 2 |\)
The importance of the use of the absolute value in the previous example is apparent when we evaluate using values that make the radicand negative. For example, when \(x = 1\),
\(\begin{aligned} \sqrt { ( x - 2 ) ^ { 2 } } & = | x - 2 | \\ & = | 1 - 2 | \\ & = | - 1 | \\ & = 1 \end{aligned}\)
Next, consider the square root of a negative number. To determine the square root of \(−25\), you must find a number that when squared results in \(−25\):
\(\sqrt { - 25 } = \color{Cerulean}{?} \color{black}\quad{ \text { or }} \quad( \color{Cerulean}{?}\color{black}{ )} ^ { 2 } = - 25\)
However, any real number squared always results in a positive number. The square root of a negative number is currently left undefined. For now, we will state that \(\sqrt { - 25 }\) is not a real number. Therefore, the square root function4 given by \(f ( x ) = \sqrt { x }\) is not defined to be a real number if the \(x\)-values are negative. The smallest value in the domain is zero. For example,\(f ( 0 ) = \sqrt { 0 } = 0\) and \(f ( 4 ) = \sqrt { 4 } = 2\). Recall the graph of the square root function.
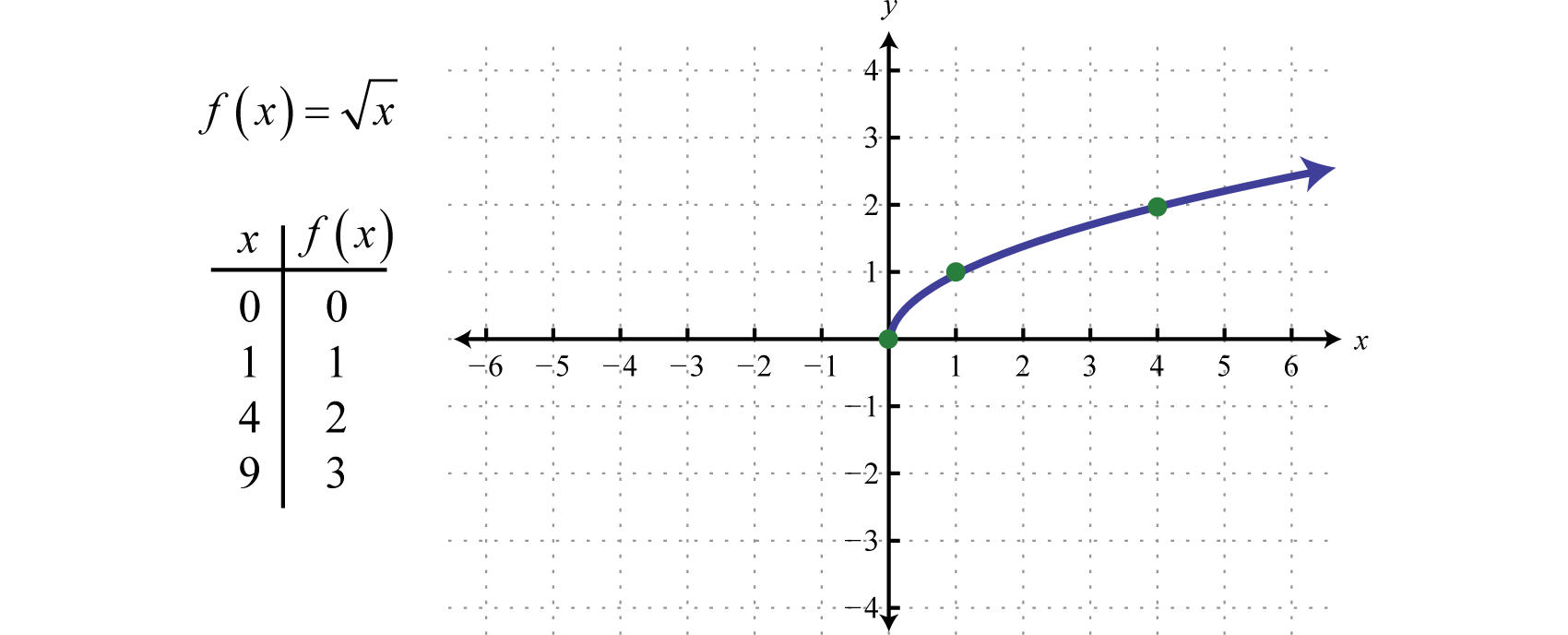
The domain and range both consist of real numbers greater than or equal to zero: \([0, ∞)\). To determine the domain of a function involving a square root we look at the radicand and find the values that produce nonnegative results.
Example \(\PageIndex{3}\):
Determine the domain of the function defined by \(f ( x ) = \sqrt { 2 x + 3 }\).
Solution
Here the radicand is \(2x + 3\). This expression must be zero or positive. In other words,
\(2 x + 3 \geq 0\)
Solve for \(x\).
\(\begin{aligned} 2 x + 3 & \geq 0 \\ 2 x & \geq - 3 \\ x & \geq - \frac { 3 } { 2 } \end{aligned}\)
Answer:
Domain: \(\left[ - \frac { 3 } { 2 } , \infty \right)\)
A cube root5 of a number is a number that when multiplied by itself three times yields the original number. Furthermore, we denote a cube root using the symbol \(\sqrt [ 3 ] { }\), where \(3\) is called the index6. For example,
\(\sqrt [ 3 ] { 64 } = 4 , \text { because } 4 ^ { 3 } = 64\)
The product of three equal factors will be positive if the factor is positive and negative if the factor is negative. For this reason, any real number will have only one real cube root. Hence the technicalities associated with the principal root do not apply. For example,
\(\sqrt [ 3 ] { - 64 } = - 4 , \text { because } ( - 4 ) ^ { 3 } = - 64\)
In general, given any real number \(a\), we have the following property:
\(\sqrt [ 3 ] { a ^ { 3 } } = a \quad \text { if } \quad a \in R\)
When simplifying cube roots, look for factors that are perfect cubes.
Example \(\PageIndex{4}\):
Evaluate.
- \(\sqrt [ 3 ] { 8 }\)
- \(\sqrt [ 3 ] { 0 }\)
- \(\sqrt [ 3 ] { \frac { 1 } { 27 } }\)
- \(\sqrt [ 3 ] { - 1 }\)
- \(\sqrt [ 3 ] { - 125 }\)
Solution
- \(\sqrt [ 3 ] { 8 } = \sqrt [ 3 ] { 2 ^ { 3 } } = 2\)
- \(\sqrt [ 3 ] { 0 } = \sqrt [ 3 ] { 0 ^ { 3 } } = 0\)
- \(\sqrt [ 3 ] { \frac { 1 } { 27 } } = \sqrt [ 3 ] { \left( \frac { 1 } { 3 } \right) ^ { 3 } } = \frac { 1 } { 3 }\)
- \(\sqrt [ 3 ] { - 1 } = \sqrt [ 3 ] { ( - 1 ) ^ { 3 } } = - 1\)
- \(\sqrt [ 3 ] { - 125 } = \sqrt [ 3 ] { ( - 5 ) ^ { 3 } } = - 5\)
It may be the case that the radicand is not a perfect square or cube. If an integer is not a perfect power of the index, then its root will be irrational. For example, \(\sqrt [ 3 ] { 2 }\) is an irrational number that can be approximated on most calculators using the root button \(\sqrt [ x ] { }\).Depending on the calculator, we typically type in the index prior to pushing the button and then the radicand as follows:
\(3 \quad\sqrt [ x ] {y }\quad2\quad=\)
Therefore, we have
\(\sqrt [ 3 ] { 2 } \approx 1.260 , \quad \text { because } \quad 1.260 ^{\wedge} 3 \approx 2\)
Since cube roots can be negative, zero, or positive we do not make use of any absolute values.
Example \(\PageIndex{5}\):
Simplify: \(\sqrt [ 3 ] { ( y - 7 ) ^ { 3 } }\).
Solution
The cube root of a quantity cubed is that quantity.
\(\sqrt [ 3 ] { ( y - 7 ) ^ { 3 } } = y - 7\)
Answer:
\(y-7\)
Exercise \(\PageIndex{1}\)
Evaluate: \(\sqrt [ 3 ] { - 1000 }\).
- Answer
-
\(=10\)
www.youtube.com/v/B06NIs-3gig
Next, consider the cube root function7:
\(f ( x ) = \sqrt [ 3 ] { x } \quad\color{Cerulean}{Cube\:root\:function.}\)
Since the cube root could be either negative or positive, we conclude that the domain consists of all real numbers. Sketch the graph by plotting points. Choose some positive and negative values for \(x\), as well as zero, and then calculate the corresponding \(y\)-values.
| \(x\) | \(f(x)\) | \(f ( x ) = \sqrt [ 3 ] { x }\) | \(\color{Cerulean}{Ordered\:Pairs}\) |
|---|---|---|---|
| \(-8\) | \(\color{Cerulean}{-2}\) | \(f ( - 8 ) = \sqrt [ 3 ] { - 8 } = - 2\) | \((-8,-2)\) |
| \(-1\) | \(\color{Cerulean}{-1}\) | \(f ( - 1 ) = \sqrt [ 3 ] { - 1 } = - 1\) | \((-1,-1)\) |
| \(0\) | \(\color{Cerulean}{0}\) | \(f ( 0 ) = \sqrt [ 3 ] { 0 } = 0\) | \((0,0)\) |
| \(1\) | \(\color{Cerulean}{1}\) | \(f ( 1 ) = \sqrt [ 3 ] { 1 } = 1\) | \((1,1)\) |
| \(8\) | \(\color{Cerulean}{2}\) | \(f ( 8 ) = \sqrt [ 3 ] { 8 } = 2\) | \((8,2)\) |
Plot the points and sketch the graph of the cube root function.
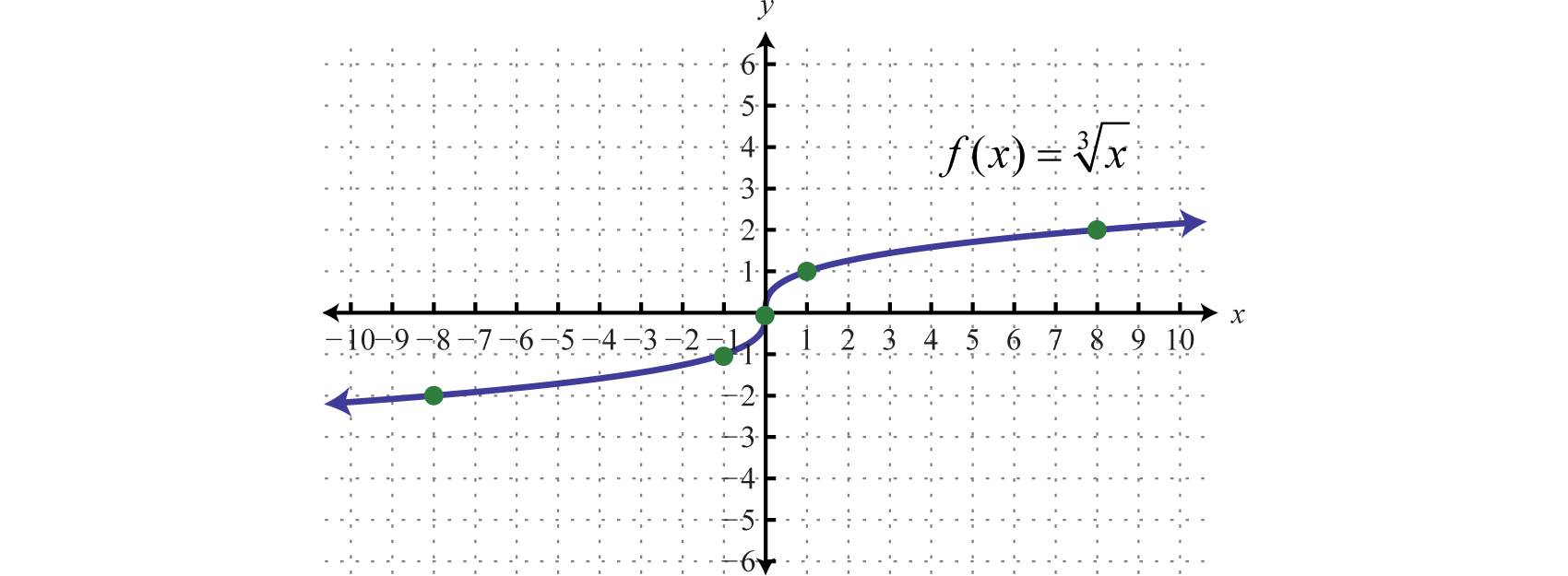
The graph passes the vertical line test and is indeed a function. In addition, the range consists of all real numbers.
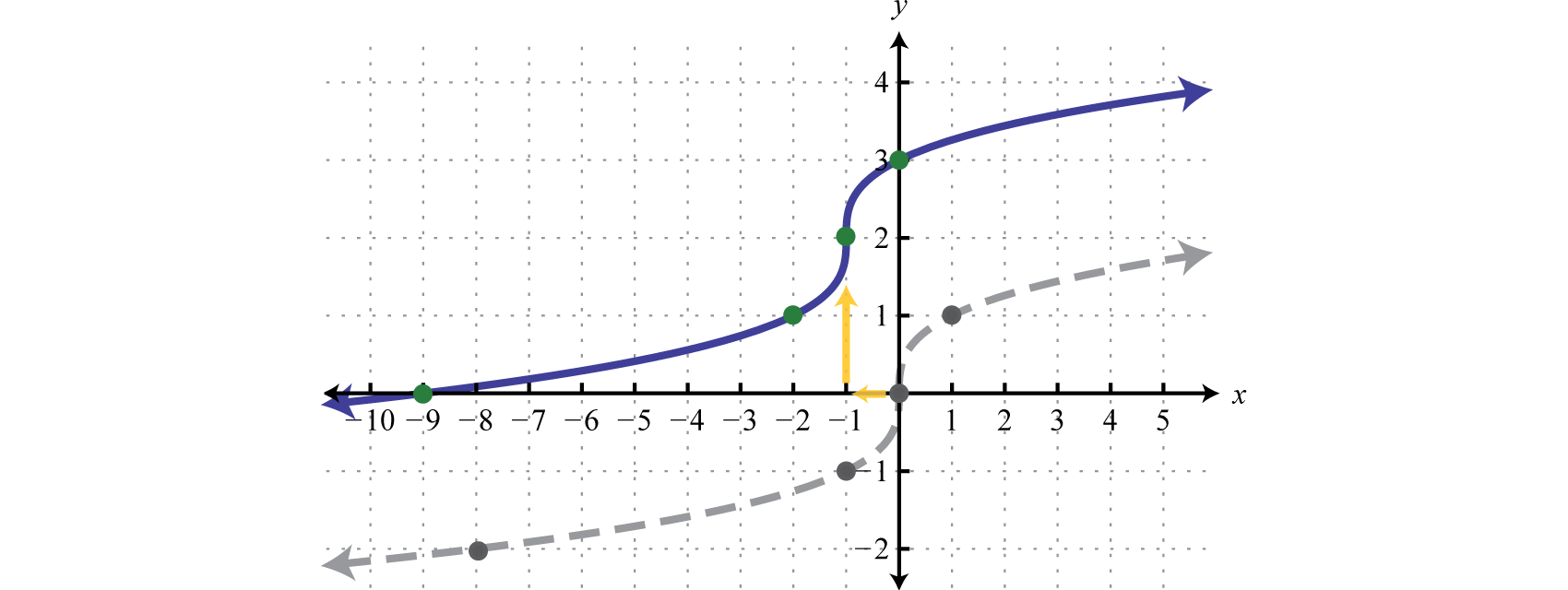
Example \(\PageIndex{6}\):
Given \(g ( x ) = \sqrt [ 3 ] { x + 1 } + 2\), find \(g ( - 9 ) , g ( - 2 ) , g ( - 1 )\), and \(g(0)\). Sketch the graph of \(g\).
Solution
Replace \(x\) with the given values.
| \(x\) | \(g(x)\) | \(g ( x ) = \sqrt [ 3 ] { x + 1 } + 2\) | \(\color{Cerulean}{Ordered\:Pairs}\) |
|---|---|---|---|
| \(-9\) | \(\color{Cerulean}{0}\) | \(g ( \color{OliveGreen}{- 9}\color{black}{ )} = \sqrt [ 3 ] { \color{OliveGreen}{- 9}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { - 8 } + 2 = - 2 + 2 = 0\) | \((-9,0)\) |
| \(-2\) | \(\color{Cerulean}{1}\) | \(g ( \color{OliveGreen}{- 2}\color{black}{ )} = \sqrt [ 3 ] {\color{OliveGreen}{ - 2}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { - 1 } + 2 = - 1 + 2 = 1\) | \((-2,1)\) |
| \(-1\) | \(\color{Cerulean}{2}\) | \(g ( \color{OliveGreen}{- 1}\color{black}{ )} = \sqrt [ 3 ] { \color{OliveGreen}{- 1}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { 0 } + 2 = 0 + 2 = 2\) | \((-1,2)\) |
| \(0\) | \(\color{Cerulean}{3}\) | \(g ( \color{OliveGreen}{0}\color{black}{ )} = \sqrt [ 3 ] { \color{OliveGreen}{0}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { 1 } + 2 = 1 + 2 = 3\) | \((0,3)\) |
We can also sketch the graph using the following translations:
\(\begin{array} { l } { y = \sqrt [ 3 ] { x } \quad\quad\quad\quad \color{Cerulean} { Basic\: cube \:root\: function } } \\ { y = \sqrt [ 3 ] { x + 1 } \quad \quad\:\color{Cerulean} { Horizontal\: shift\: left\: 1\: unit } } \\ { y = \sqrt [ 3 ] { x + 1 } + 2 \:\:\:\color{Cerulean} { Vertical\: shift\: up\: 2\: units } } \end{array}\)
Answer:
\(n\)th Roots
For any integer \(n ≥ 2\), we define an \(n\)th root8 of a positive real number as a number that when raised to the \(n\)th power yields the original number. Given any nonnegative real number \(a\), we have the following property:
\(\sqrt [ n ] { a ^ { n } } = a , \quad \text { if } \quad a \geq 0\)
Here n is called the index and \(a^{n}\) is called the radicand. Furthermore, we can refer to the entire expression \(\sqrt [ n ] { A }\) as a radical9. When the index is an integer greater than or equal to \(4\), we say “fourth root,” “fifth root,” and so on. The \(n\)th root of any number is apparent if we can write the radicand with an exponent equal to the index.
Example \(\PageIndex{7}\):
Simplify:
- \(\sqrt [ 4 ] { 81 }\)
- \(\sqrt [ 5 ] { 32 }\)
- \(\sqrt [ 7 ] { 1 }\)
- \(\sqrt [ 4 ] { \frac { 1 } { 16 } }\)
Solution
- \(\sqrt [ 4 ] { 81 } = \sqrt [ 4 ] { 3 ^ { 4 } } = 3\)
- \(\sqrt [ 5 ] { 32 } = \sqrt [ 5 ] { 2 ^ { 5 } } = 2\)
- \(\sqrt [ 7 ] { 1 } = \sqrt [ 7 ] { 1 ^ { 7 } } = 1\)
- \(\sqrt [ 4 ] { \frac { 1 } { 16 } } = \sqrt [ 4 ] { \left( \frac { 1 } { 2 } \right) ^ { 4 } } = \frac { 1 } { 2 }\)
Note
If the index is \(n = 2\), then the radical indicates a square root and it is customary to write the radical without the index; \(\sqrt [ 2 ] { a } = \sqrt { a }\).
We have already taken care to define the principal square root of a real number. At this point, we extend this idea to nth roots when n is even. For example, \(3\) is a fourth root of \(81\), because \(3^{4} = 81\). And since \((−3)^{4} = 81\), we can say that \(−3\) is a fourth root of \(81\) as well. Hence we use the radical sign \(\sqrt [ n ] { }\) to denote the principal (nonnegative) \(n\)th root10 when \(n\) is even. In this case, for any real number \(a\), we use the following property:
\(\sqrt [ n ] { a ^ { n } } = | a | \quad \color{Cerulean} { When\:n\:is\:even } \)
For example,
\(\begin{aligned} \sqrt [ 4 ] { 81 } & = \sqrt [ 4 ] { 3 ^ { 4 } } \quad\quad= |3| \:\:\:\:\:= 3 \\ \sqrt [ 4 ] { 81 } & = \sqrt [ 4 ] { ( - 3 ) ^ { 4 } } \:\:= | - 3 | = 3 \end{aligned}\)
The negative \(n\)th root, when \(n\) is even, will be denoted using a negative sign in front of the radical \(- \sqrt [ n ] { }\).
\(- \sqrt [ 4 ] { 81 } = - \sqrt [ 4 ] { 3 ^ { 4 } } = - 3\)
We have seen that the square root of a negative number is not real because any real number that is squared will result in a positive number. In fact, a similar problem arises for any even index:
\(\sqrt [ 4 ] { - 81 } =\color{Cerulean}{ ?} \quad \color{black}{\text { or }} \quad (\color{Cerulean}{ ?}\color{black}{ )} ^ { 4 } = - 81\)
We can see that a fourth root of \(−81\) is not a real number because the fourth power of any real number is always positive.
\(\left. \begin{array} { l } { \sqrt { - 4 } } \\ { \sqrt [ 4 ] { - 81 } } \\ { \sqrt [ 6 ] { - 64 } } \end{array} \right\} \quad \color{Cerulean}{These\:radicals\:are\:not\:real\:numbers.}\)
You are encouraged to try all of these on a calculator. What does it say?
Example \(\PageIndex{8}\):
Simplify.
- \(\sqrt [ 4 ] { ( - 10 ) ^ { 4 } }\)
- \(\sqrt [ 4 ] { - 10 ^ { 4 } }\)
- \(\sqrt [ 6 ] { ( 2 y + 1 ) ^ { 6 } }\)
Solution
Since the indices are even, use absolute values to ensure nonnegative results.
- \(\sqrt [ 4 ] { ( - 10 ) ^ { 4 } } = | - 10 | = 10\)
- \(\sqrt [ 4 ] { - 10 ^ { 4 } } = \sqrt [ 4 ] { - 10,000 }\) is not a real number.
- \(\sqrt [ 6 ] { ( 2 y + 1 ) ^ { 6 } } = | 2 y + 1 |\)
When the index \(n\) is odd, the same problems do not occur. The product of an odd number of positive factors is positive and the product of an odd number of negative factors is negative. Hence when the index \(n\) is odd, there is only one real \(n\)th root for any real number \(a\). And we have the following property:
\(\sqrt [ n ] { a ^ { n } } = a \quad \color{Cerulean} { When \: n\:is\:odd}\)
Example \(\PageIndex{9}\):
Simplify.
- \(\sqrt [ 5 ] { ( - 10 ) ^ { 5 } }\)
- \(\sqrt [ 5 ] { - 32 }\)
- \(\sqrt [ 7 ] { ( 2 y + 1 ) ^ { 7 } }\)
Solution
Since the indices are odd, the absolute value is not used.
- \(\sqrt [ 5 ] { ( - 10 ) ^ { 5 } } = - 10\)
- \(\sqrt [ 5 ] { - 32 } = \sqrt [ 5 ] { ( - 2 ) ^ { 5 } } = - 2\)
- \(\sqrt [ 7 ] { ( 2 y + 1 ) ^ { 7 } } = 2 y + 1\)
In summary, for any real number \(a\) we have,
\(\begin{aligned} \sqrt [ n ] { a^ { n } } & = | a | \color{Cerulean}\:\:\: { When \: n\: is\: even } \\ \sqrt [ n ] {a^ { n } } & = a \quad\: \color{Cerulean} { When \: n\: is\: odd } \end{aligned}\)
When \(n\) is odd, the \(n\)th root is positive or negative depending on the sign of the radicand.
\(\begin{aligned} \sqrt [ 3 ] { 27 } & = \sqrt [ 3 ] { 3 ^ { 3 } } = 3 \\ \sqrt [ 3 ] { - 27 } & = \sqrt [ 3 ] { ( - 3 ) ^ { 3 } } = - 3 \end{aligned}\)
When \(n\) is even, the \(n\)th root is positive or not real depending on the sign of the radicand.
\(\begin{aligned} \sqrt [ 4 ] { 16 } & = \sqrt [ 4 ] { 2 ^ { 4 } } \quad\:\:= 2 \\ \sqrt [ 4 ] { 16 } & = \sqrt [ 4 ] { ( - 2 ) ^ { 4 } } = | - 2| = 2 \\ \sqrt [ 4 ] { - 16 } & \quad\color{Cerulean} { Not \:a \:real\: number } \end{aligned}\)
Exercise \(\PageIndex{2}\)
Simplify: \(- 8 \sqrt [ 5 ] { - 32 }\).
- Answer
-
\(16\)
www.youtube.com/v/Ik1xXgq18f0
Simplifying Radicals
It will not always be the case that the radicand is a perfect power of the given index. If it is not, then we use the product rule for radicals11 and the quotient rule for radicals12 to simplify them. Given real numbers \(\sqrt [ n ] { A }\) and \(\sqrt [ n ] { B }\),
| Product Rule for Radicals: | \(\sqrt [ n ] { A \cdot B } = \sqrt [ n ] { A } \cdot \sqrt [ n ] { B }\) |
|---|---|
| Quotient Rule for Radicals: | \(\sqrt [ n ] { \frac { A } { B } } = \frac { \sqrt [ n ] { A } } { \sqrt [ n ] { B } }\) |
A radical is simplified13 if it does not contain any factors that can be written as perfect powers of the index.
Example \(\PageIndex{10}\):
Simplify: \(\sqrt { 150 }\).
Solution
Here \(150\) can be written as \(2 \cdot 3 \cdot 5 ^ { 2 }\).
\(\begin{aligned} \sqrt { 150 } & = \sqrt { 2 \cdot 3 \cdot 5 ^ { 2 } }\quad\quad \color{Cerulean} { Apply\: the\: product \:rule\: for\: radicals.} \\ & = \sqrt { 2 \cdot 3 } \cdot \sqrt { 5 ^ { 2 } }\quad\: \color{Cerulean} { Simplify. } \\ & = \sqrt { 6 } \cdot 5 \\ & = 5 \sqrt { 6 } \end{aligned}\)
We can verify our answer on a calculator:
\(\sqrt { 150 } \approx 12.25 \quad\text { and }\quad 5 \sqrt { 6 } \approx 12.25\)
Also, it is worth noting that
\(12.25 ^ { 2 } \approx 150\)
Answer:
\(5 \sqrt { 6 }\)
Note
\(5 \sqrt { 6 }\) is the exact answer and \(12.25\) is an approximate answer. We present exact answers unless told otherwise.
Example \(\PageIndex{11}\):
Simplify: \(\sqrt [ 3 ] { 160 }\).
Solution
Use the prime factorization of \(160\) to find the largest perfect cube factor:
\(\begin{aligned} 160 & = 2 ^ { 5 } \cdot 5 \\ & = \color{Cerulean}{2 ^ { 3} }\color{black}{ \cdot} 2 ^ { 2 } \cdot 5 \end{aligned}\)
Replace the radicand with this factorization and then apply the product rule for radicals.
\(\begin{aligned} \sqrt [ 3 ] { 160 } & = \sqrt [ 3 ] { 2 ^ { 3 } \cdot 2 ^ { 2 } \cdot 5 } \quad\quad\color{Cerulean} { Apply\:the\: product\: rule\: for\: radicals.} \\ & = \sqrt [ 3 ] { 2 ^ { 3 } } \cdot \sqrt [ 3 ] { 2 ^ { 2 } \cdot 5 }\quad \color{Cerulean} { Simplify. } \\ & = 2 \cdot \sqrt [ 3 ] { 20 } \end{aligned}\)
We can verify our answer on a calculator.
\(\sqrt [ 3 ] { 160 } \approx 5.43 \text { and } 2 \sqrt [ 3 ] { 20 } \approx 5.43\)
Answer:
\(2 \sqrt [ 3 ] { 20 }\)
Example \(\PageIndex{12}\):
Simplify: \(\sqrt [ 5 ] { - 320 }\).
Solution
Here we note that the index is odd and the radicand is negative; hence the result will be negative. We can factor the radicand as follows:
\(- 320 = - 1 \cdot 32 \cdot 10 = ( - 1 ) ^ { 5 } \cdot ( 2 ) ^ { 5 } \cdot 10\)
Then simplify:
\(\begin{aligned} \sqrt [ 5 ] { - 320 } & = \sqrt [ 5 ] { ( - 1 ) ^ { 5 } \cdot ( 2 ) ^ { 5 } \cdot 10 } \quad\quad\quad\color{Cerulean} { Apply\: the\: product\: rule\: for\: radicals.} \\ & = \sqrt [ 5 ] { ( - 1 ) ^ { 5 } } \cdot \sqrt [ 5 ] { ( 2 ) ^ { 5 } } \cdot \sqrt [ 5 ] { 10 }\quad \color{Cerulean} { Simplify. } \\ &= -1\cdot2\cdot \sqrt[5]{10} \\ &=-2\cdot \sqrt[5]{10}\end{aligned}\)
Answer:
\(- 2 \sqrt [ 5 ] { 10 }\)
Example \(\PageIndex{13}\):
Simplify: \(\sqrt [ 3 ] { - \frac { 8 } { 64 } }\).
Solution
In this case, consider the equivalent fraction with \(−8 = (−2)^{3}\) in the numerator and \(64 = 4^{3}\) in the denominator and then simplify.
\(\begin{aligned} \sqrt [ 3 ] { - \frac { 8 } { 64 } } & = \sqrt [ 3 ] { \frac { - 8 } { 64 } } \quad\quad\quad\color{Cerulean} { Apply\: the\: quotient \:rule\: for\: radicals.} \\ & = \frac { \sqrt [ 3 ] { ( - 2 ) ^ { 3 } } } { \sqrt [ 3 ] { 4 ^ { 3 } } }\quad\:\:\: \color{Cerulean} { Simplify. } \\ & = \frac { - 2 } { 4 } \\ & = - \frac { 1 } { 2 } \end{aligned}\)
Answer:
\(-\frac{1}{2}\)
Exercise \(\PageIndex{3}\)
Simplify: \(\sqrt [ 4 ] { \frac { 80 } { 81 } }\)
- Answer
-
\(\frac { 2 \sqrt [ 4 ] { 5 } } { 3 }\)
www.youtube.com/v/8CwbDBFO2FQ
Key Takeaways
- To simplify a square root, look for the largest perfect square factor of the radicand and then apply the product or quotient rule for radicals.
- To simplify a cube root, look for the largest perfect cube factor of the radicand and then apply the product or quotient rule for radicals.
- When working with nth roots, \(n\) determines the definition that applies. We use \(\sqrt [ n ] { a ^ { n } } = a _ { 1 }\) when \(n\) is odd and \(\sqrt [ n ] { a ^ { n } } = | a | \) when \(n\) is even.
- To simplify \(n\)th roots, look for the factors that have a power that is equal to the index \(n\) and then apply the product or quotient rule for radicals. Typically, the process is streamlined if you work with the prime factorization of the radicand.
Exercise \(\PageIndex{4}\)
Simplify.
- \(\sqrt { 36 }\)
- \(\sqrt { 100 }\)
- \(\sqrt { \frac { 4 } { 9 } }\)
- \(\sqrt { \frac { 1 } { 64 } }\)
- \(- \sqrt { 16 }\)
- \(- \sqrt { 1 }\)
- \(\sqrt { ( - 5 ) ^ { 2 } }\)
- \(\sqrt { ( - 1 ) ^ { 2 } }\)
- \(\sqrt { - 4 }\)
- \(\sqrt { - 5 ^ { 2 } }\)
- \(- \sqrt { ( - 3 ) ^ { 2 } }\)
- \(- \sqrt { ( - 4 ) ^ { 2 } }\)
- \(\sqrt { x ^ { 2 } }\)
- \(\sqrt { ( - x ) ^ { 2 } }\)
- \(\sqrt { ( x - 5 ) ^ { 2 } }\)
- \(\sqrt { ( 2 x - 1 ) ^ { 2 } }\)
- \(\sqrt [ 3 ] { 64 }\)
- \(\sqrt [ 3 ] { 216 }\)
- \(\sqrt [ 3 ] { - 216 }\)
- \(\sqrt [ 3 ] { - 64 }\)
- \(\sqrt [ 3 ] { - 8 }\)
- \(\sqrt [ 3 ] { 1 }\)
- \(- \sqrt [ 3 ] { ( - 2 ) ^ { 3 } }\)
- \(- \sqrt [ 3 ] { ( - 7 ) ^ { 3 } }\)
- \(\sqrt [ 3 ] { \frac { 1 } { 8 } }\)
- \(\sqrt [ 3 ] { \frac { 8 } { 27 } }\)
- \(\sqrt [ 3 ] { ( - y ) ^ { 3 } }\)
- \(- \sqrt [ 3 ] { y ^ { 3 } }\)
- \(\sqrt [ 3 ] { ( y - 8 ) ^ { 3 } }\)
- \(\sqrt [ 3 ] { ( 2 x - 3 ) ^ { 3 } }\)
- Answer
-
1. \(6\)
3. \(\frac{2}{3}\)
5. \(−4\)
7. \(5\)
9. Not a real number
11. \(−3\)
13. \(|x|\)
15. \(|x − 5|\)
17. \(4\)
19. \(−6\)
21. \(−2\)
23. \(2\)
25. \(\frac{1}{2}\)
27. \(−y\)
29. \(y − 8\)
Exercise \(\PageIndex{5}\)
Determine the domain of the given function.
- \(g ( x ) = \sqrt { x + 5 }\)
- \(g ( x ) = \sqrt { x - 2 }\)
- \(f ( x ) = \sqrt { 5 x + 1 }\)
- \(f ( x ) = \sqrt { 3 x + 4 }\)
- \(g ( x ) = \sqrt { - x + 1 }\)
- \(g ( x ) = \sqrt { - x - 3 }\)
- \(h ( x ) = \sqrt { 5 - x }\)
- \(h ( x ) = \sqrt { 2 - 3 x }\)
- \(g ( x ) = \sqrt [ 3 ] { x + 4 }\)
- \(g ( x ) = \sqrt [ 3 ] { x - 3 }\)
- Answer
-
1. \([ - 5 , \infty )\)
3. \(\left[ - \frac { 1 } { 5 } , \infty \right)\)
5. \(( - \infty , 1 ]\)
7. \(( - \infty , 5 ]\)
9. \(( - \infty , \infty )\)
Exercise \(\PageIndex{6}\)
Evaluate given the function definition.
- Given \(f ( x ) = \sqrt { x - 1 }\), find \(f ( 1 ) , f ( 2 )\), and \(f ( 5 )\)
- Given \(f ( x ) = \sqrt { x + 5 }\), find \(f ( - 5 ) , f ( - 1 )\), and \(f ( 20 )\)
- Given \(f ( x ) = \sqrt { x } + 3\), find \(f ( 0 ) , f ( 1 )\), and \(f(16)\)
- Given \(f ( x ) = \sqrt { x } - 5\), find \(f ( 0 ) , f ( 1 )\), and \(f(25)\)
- Given \(g ( x ) = \sqrt [ 3 ] { x }\), find \(g ( - 1 ) , g ( 0 )\), and \(g(1)\)
- Given \(g ( x ) = \sqrt [ 3 ] { x } - 2\) find \(g ( - 1 ) , g ( 0 )\), and \(g(8)\)
- Given \(g ( x ) = \sqrt [ 3 ] { x + 7 }\), find \(g ( - 15 ) , g ( - 7 )\), and \(g(20)\)
- Given \(g ( x ) = \sqrt [ 3 ] { x - 1 } + 2\), find \(g ( 0 ) , g ( 2 ) \), and \(g(9)\)
- Answer
-
1. \(f ( 1 ) = 0 ; f ( 2 ) = 1 ; f ( 5 ) = 2\)
3. \(f ( 0 ) = 3 ; f ( 1 ) = 4 ; f ( 16 ) = 7\)
5. \(g ( - 1 ) = - 1 ; g ( 0 ) = 0 ; g ( 1 ) = 1\)
7. \(g ( - 15 ) = - 2 ; g ( - 7 ) = 0 ; g ( 20 ) = 3\)
Exercise \(\PageIndex{7}\)
Sketch the graph of the given function and give its domain and range.
- \(f ( x ) = \sqrt { x + 9 }\)
- \(f ( x ) = \sqrt { x - 3 }\)
- \(f ( x ) = \sqrt { x - 1 } + 2\)
- \(f ( x ) = \sqrt { x + 1 } + 3\)
- \(g ( x ) = \sqrt [ 3 ] { x - 1 }\)
- \(g ( x ) = \sqrt [ 3 ] { x + 1 }\)
- \(g ( x ) = \sqrt [ 3 ] { x } - 4\)
- \(g ( x ) = \sqrt [ 3 ] { x } + 5\)
- \(g ( x ) = \sqrt [ 3 ] { x + 2 } - 1\)
- \(g ( x ) = \sqrt [ 3 ] { x - 2 } + 3\)
- \(f ( x ) = - \sqrt [ 3 ] { x }\)
- \(f ( x ) = - \sqrt [ 3 ] { x - 1 }\)
- Answer
-
1. Domain: \([ - 9 , \infty )\); range: \([ 0 , \infty )\)
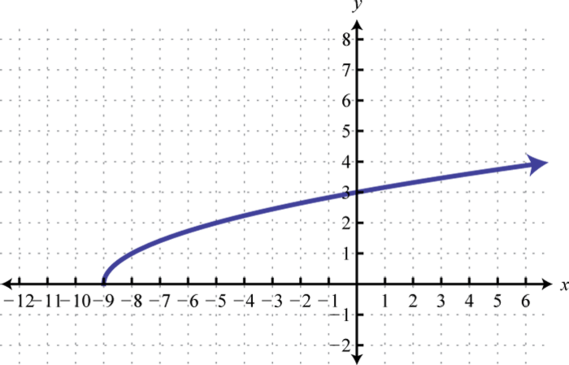
Figure \(\PageIndex{4}\) 3. Domain: \([ 1 , \infty )\); range: \([ 2 , \infty )\)
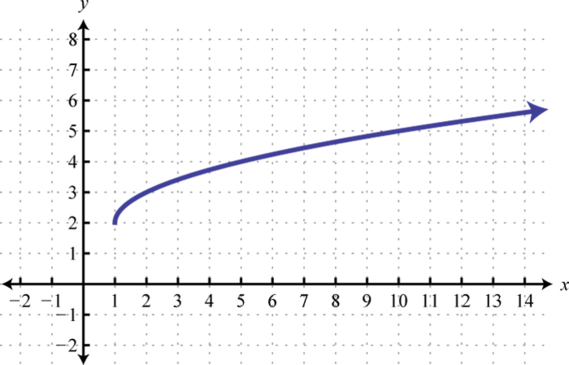
Figure \(\PageIndex{5}\) 5. Domain: \(\mathbb { R }\); range; \(\mathbb { R }\)
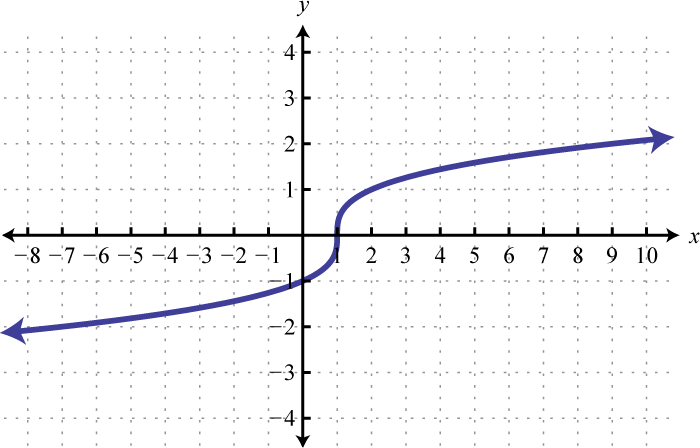
Figure \(\PageIndex{6}\) 7. Domain: \(\mathbb { R }\); range; \(\mathbb { R }\)
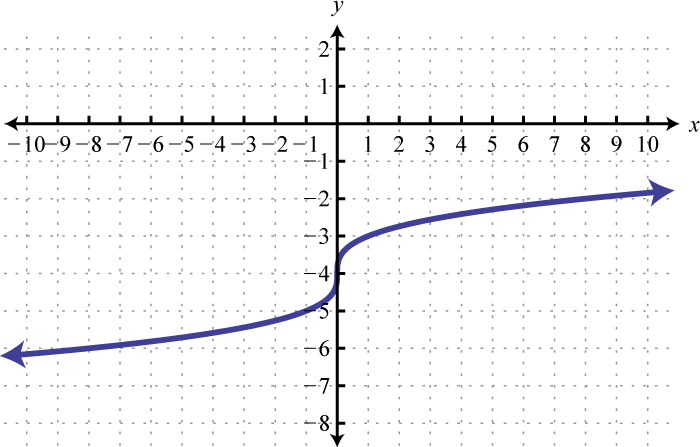
Figure \(\PageIndex{7}\) 9. Domain: \(\mathbb { R }\); range; \(\mathbb { R }\)
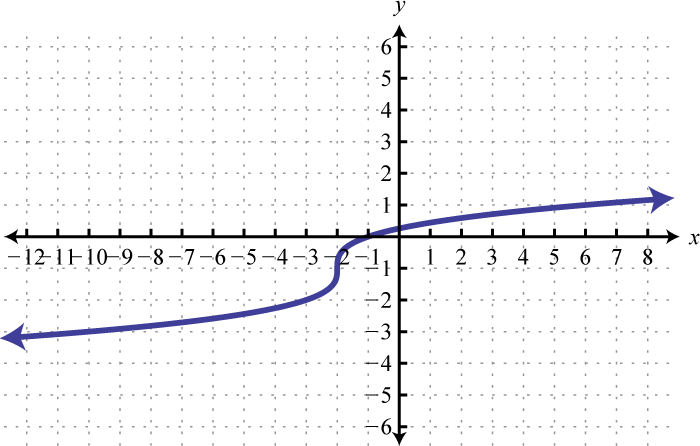
Figure \(\PageIndex{8}\) 11. Domain: \(\mathbb { R }\); range; \(\mathbb { R }\)
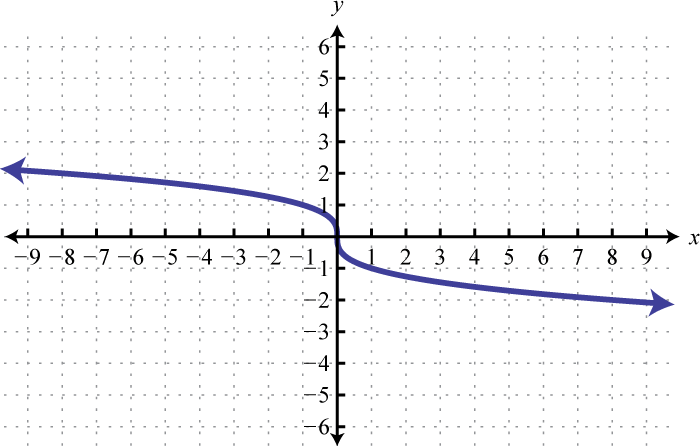
Figure \(\PageIndex{9}\)
Exercise \(\PageIndex{8}\)
Simplify.
- \(\sqrt [ 4 ] { 64 }\)
- \(\sqrt [ 4 ] { 16 }\)
- \(\sqrt [ 4 ] { 625 }\)
- \(\sqrt [ 4 ] { 1 }\)
- \(\sqrt [ 4 ] { 256 }\)
- \(\sqrt [ 4 ] { 10,000 }\)
- \(\sqrt [ 5 ] { 243 }\)
- \(\sqrt [ 5 ] { 100,000 }\)
- \(\sqrt [ 5 ] { \frac { 1 } { 32 } }\)
- \(\sqrt [ 5 ] { \frac { 1 } { 243 } }\)
- \(- \sqrt [ 4 ] { 16 }\)
- \(- \sqrt [ 6 ] { 1 }\)
- \(\sqrt [ 5 ] { - 32 }\)
- \(\sqrt [ 5 ] { - 1 }\)
- \(\sqrt { - 1 }\)
- \(\sqrt [ 4 ] { - 16 }\)
- \(- 6 \sqrt [ 3 ] { - 27 }\)
- \(- 5 \sqrt [ 3 ] { - 8 }\)
- \(2 \sqrt [ 3 ] { - 1,000 }\)
- \(7 \sqrt [ 5 ] { - 243 }\)
- \(6 \sqrt [ 4 ] { - 16 }\)
- \(12 \sqrt [ 6 ] { - 64 }\)
- \(\sqrt [ 3 ] { \frac { 25 } { 16 } }\)
- \(6 \sqrt { \frac { 16 } { 9 } }\)
- \(5 \sqrt [ 3 ] { \frac { 27 } { 125 } }\)
- \(7 \sqrt [ 5 ] { \frac { 32 } { 7 ^ { 5 } } }\)
- \(- 5 \sqrt [ 3 ] { \frac { 8 } { 27 } }\)
- \(- 8 \sqrt [ 4 ] { \frac { 625 } { 16 } }\)
- \(2 \sqrt [ 5 ] { 100,000 }\)
- \(2 \sqrt [ 7 ] { 128 }\)
- Answer
-
1. \(4\)
3. \(5\)
5. \(4\)
7. \(3\)
9. \(\frac{1}{2}\)
11. \(−2\)
13. \(−2\)
15. Not a real number
17. \(18\)
19. \(−20\)
21. Not a real number
23. \(\frac{15}{4}\)
25. \(3\)
27. \(−\frac{10}{3}\)
29. \(20\)
Exercise \(\PageIndex{9}\)
Simplify.
- \(\sqrt { 96 }\)
- \(\sqrt { 500 }\)
- \(\sqrt { 480 }\)
- \(\sqrt { 450 }\)
- \(\sqrt { 320 }\)
- \(\sqrt { 216 }\)
- \(5 \sqrt { 112 }\)
- \(10 \sqrt { 135 }\)
- \(- 2 \sqrt { 240 }\)
- \(- 3 \sqrt { 162 }\)
- \(\sqrt { \frac { 150 } { 49 } }\)
- \(\sqrt { \frac { 200 } { 9 } }\)
- \(\sqrt { \frac { 675 } { 121 } }\)
- \(\sqrt { \frac { 192 } { 81 } }\)
- \(\sqrt [ 3 ] { 54 }\)
- \(\sqrt [ 3 ] { 24 }\)
- \(\sqrt [ 3 ] { 48 }\)
- \(\sqrt [ 3 ] { 81 }\)
- \(\sqrt [ 3 ] { 40 }\)
- \(\sqrt [ 3 ] { 120 }\)
- \(\sqrt [ 3 ] { 162 }\)
- \(\sqrt [ 3 ] { 500 }\)
- \(\sqrt [ 3 ] { \frac { 54 } { 125 } }\)
- \(\sqrt [ 3 ] { \frac { 40 } { 343 } }\)
- \(5 \sqrt [ 3 ] { - 48 }\)
- \(2 \sqrt [ 3 ] { - 108 }\)
- \(8 \sqrt [ 4 ] { 96 }\)
- \(7 \sqrt [ 4 ] { 162 }\)
- \(\sqrt [ 5 ] { 160 }\)
- \(\sqrt [ 5 ] { 486 }\)
- \(\sqrt [ 5 ] { \frac { 224 } { 243 } }\)
- \(\sqrt [ 5 ] { \frac { 5 } { 32 } }\)
- \(\sqrt [ 5 ] { - \frac { 1 } { 32 } }\)
- \(\sqrt [ 6 ] { - \frac { 1 } { 64 } }\)
- Answer
-
1. \(4 \sqrt { 6 }\)
3. \(4 \sqrt { 30 }\)
5. \(8 \sqrt { 5 }\)
7. \(20 \sqrt { 7 }\)
9. \(- 8 \sqrt { 15 }\)
11. \(\frac { 5 \sqrt { 6 } } { 7 }\)
13. \(\frac { 15 \sqrt { 3 } } { 11 }\)
15. \(3 \sqrt [ 3 ] { 2 }\)
17. \(2 \sqrt [ 3 ] { 6 }\)
19. \(2 \sqrt [ 3 ] { 5 }\)
21. \(3 \sqrt [ 3 ] { 6 }\)
23. \(\frac { 3 \sqrt [ 3 ] { 2 } } { 5 }\)
25. \(- 10 \sqrt [ 3 ] { 6 }\)
27. \(16 \sqrt [ 4 ] { 6 }\)
29. \(2 \sqrt [ 5 ] { 5 }\)
31. \(\frac { 2 \sqrt [ 5 ] { 7 } } { 3 }\)
33. \(- \frac { 1 } { 2 }\)
Exercise \(\PageIndex{10}\)
Simplify. Give the exact answer and the approximate answer rounded to the nearest hundredth.
- \(\sqrt { 60 }\)
- \(\sqrt { 600 }\)
- \(\sqrt { \frac { 96 } { 49 } }\)
- \(\sqrt { \frac { 192 } { 25 } }\)
- \(\sqrt [ 3 ] { 240 }\)
- \(\sqrt [ 3 ] { 320 }\)
- \(\sqrt [ 3 ] { \frac { 288 } { 125 } }\)
- \(\sqrt [ 3 ] { \frac { 625 } { 8 } }\)
- \(\sqrt [ 4 ] { 486 }\)
- \(\sqrt [ 5 ] { 288 }\)
- Answer
-
1. \(2 \sqrt { 15 } ; 7.75\)
3. \(\frac { 4 \sqrt { 6 } } { 7 } ; 1.40\)
5. \(2 \sqrt [ 3 ] { 30 } ; 6.21\)
7. \(\frac { 2 \sqrt [ 3 ] { 36 } } { 5 } ; 1.32\)
9. \(3 \sqrt [ 4 ] { 6 } ; 4.70\)
Exercise \(\PageIndex{11}\)
Rewrite the following as a radical expression with coeffecient \(1\).
- \(2 \sqrt { 15 }\)
- \(3 \sqrt { 7 }\)
- \(5 \sqrt { 10 }\)
- \(10 \sqrt { 3 }\)
- \(2 \sqrt [ 3 ] { 7 }\)
- \(3 \sqrt [ 3 ] { 6 }\)
- \(2 \sqrt [ 4 ] { 5 }\)
- \(3\sqrt [ 4 ] { 2 }\)
- Each side of a square has a length that is equal to the square root of the square’s area. If the area of a square is \(72\) square units, find the length of each of its sides.
- Each edge of a cube has a length that is equal to the cube root of the cube’s volume. If the volume of a cube is \(375\) cubic units, find the length of each of its edges.
- The current \(I\) measured in amperes is given by the formula \(I = \sqrt { \frac { P } { R } }\) where \(P\) is the power usage measured in watts and \(R\) is the resistance measured in ohms. If a \(100\) watt light bulb has \(160\) ohms of resistance, find the current needed. (Round to the nearest hundredth of an ampere.)
- The time in seconds an object is in free fall is given by the formula \(t = \frac { \sqrt { s } } { 4 }\) where \(s\) represents the distance in feet the object has fallen. How long will it take an object to fall to the ground from the top of an \(8\)-foot stepladder? (Round to the nearest tenth of a second.)
- Answer
-
1. \(\sqrt { 60 }\)
3. \(\sqrt { 250 }\)
5. \(\sqrt [ 3 ] { 56 }\)
7. \(\sqrt [ 4 ] { 80 }\)
9. \(6 \sqrt { 2 }\) units
11. \(0.79\) ampere
Exercise \(\PageIndex{12}\)
- Explain why there are two real square roots for any positive real number and one real cube root for any real number.
- What is the square root of \(1\) and what is the cube root of \(1\)? Explain why.
- Explain why \(\sqrt { - 1 }\) is not a real number and why \(\sqrt [ 3 ] { - 1 }\) is a real number.
- Research and discuss the methods used for calculating square roots before the common use of electronic calculators.
- Answer
-
1. Answer may vary
3. Answer may vary
Footnotes
1A number that when multiplied by itself yields the original number.
2The positive square root of a positive real number, denoted with the symbol \(√\).
3The expression \(A\) within a radical sign, \(\sqrt [ n ] { A }\).
4The function defined by \(f ( x ) = \sqrt { x }\).
5A number that when used as a factor with itself three times yields the original number, denoted with the symbol \(\sqrt [ 3 ] { }\).
6The positive integer \(n\) in the notation \(\sqrt [ n ] { }\) that is used to indicate an nth root.
7The function defined by \(f ( x ) = \sqrt [ 3 ] { x }\).
8A number that when raised to the \(n\)th power \((n ≥ 2)\) yields the original number.
9Used when referring to an expression of the form \(\sqrt [ n ] { A }\).
10The positive \(n\)th root when \(n\) is even.
11Given real numbers \(\sqrt [ n ] { A }\) and \(\sqrt [ n ] { B }\),\(\sqrt [ n ] { A \cdot B } = \sqrt [ n ] { A } \cdot \sqrt [ n ] { B }\).
12Given real numbers \(\sqrt [ n ] { A }\) and \(\sqrt [ n ] { B }\),\(\sqrt [ n ] { \frac { A } { B } } = \frac { \sqrt [ n ] { A } } { \sqrt [ n ] { B } }\) where \(B ≠ 0\).
13A radical where the radicand does not consist of any factors that can be written as perfect powers of the index.


