9.1: Introduction to Sequences and Series
- Page ID
- 6247
Skills to Develop
- Find any element of a sequence given a formula for its general term.
- Use sigma notation and expand corresponding series.
- Distinguish between a sequence and a series.
- Calculate the \(n\)th partial sum of sequence.
Sequences
A sequence1 is a function whose domain is a set of consecutive natural numbers beginning with \(1\). For example, the following equation with domain \(\{1,2,3, \dots\}\) defines an infinite sequence2:
\(a(n)=5 n-3\) or \(a_{n}=5 n-3\)
The elements in the range of this function are called terms of the sequence. It is common to define the \(n\)th term, or the general term of a sequence3, using the subscripted notation \(a_{n}\), which reads “\(a\) sub \(n\).” Terms can be found using substitution as follows:
\(\begin{aligned}\color{Cerulean} { General\: term: } \quad &\color{black}{a_{n}=5 n-3} \\ \color{Cerulean} { First\: term (n=1) :}\quad & \color{black}{a_{1}=}5(\color{Cerulean}{1}\color{black}{)}-3=2 \\ \color{Cerulean}{Second\:term(n=2):} \quad& \color{black}{a_{2}=5}(\color{Cerulean}{2}\color{black}{)}-3=7 \\ \color{Cerulean}{Third\:term(n=3):} \quad& \color{black}{a_{3}=5}(\color{Cerulean}{3}\color{black}{)}-3=12 \\\color{Cerulean}{Fourth\:term(n=4):} \quad& \color{black}{a_{4}=5}(\color{Cerulean}{4}\color{black}{)}-3=17 \\ \color{Cerulean}{Fifth\:term(n=5):} \quad& \color{black}{a_{5}=5}(\color{Cerulean}{5}\color{black}{)}-3=22 \\ \vdots\end{aligned}\)
This produces an ordered list,
\(2,7,12,17,22, \ldots\)
The ellipsis \((…)\) indicates that this sequence continues forever. Unlike a set, order matters. If the domain of a sequence consists of natural numbers that end, such as \(\{1,2,3, \ldots, k\}\), then it is called a finite sequence4.
Example \(\PageIndex{1}\):
Given the general term of a sequence, find the first \(5\) terms as well as the \(100^{th}\) term: \(a_{n}=\frac{n(n-1)}{2}\).
Solution:
To find the first \(5\) terms, substitute \(1, 2, 3, 4\), and \(5\) for \(n\) and then simplify.
\(\begin{array}{l}{a_{1}=\frac{\color{Cerulean}{1}\color{black}{(}\color{Cerulean}{1}\color{black}{-}1)}{2}=\frac{1(0)}{2}=\frac{0}{2}=0} \\ {a_{2}=\frac{\color{Cerulean}{2}\color{black}{(}\color{Cerulean}{2}\color{black}{-}1)}{2}=\frac{2(1)}{2}=\frac{2}{2}=1} \\ {a_{3}=\frac{\color{Cerulean}{3}\color{black}{(}\color{Cerulean}{3}\color{black}{-}1)}{2}=\frac{3(2)}{2}=\frac{6}{2}=3} \\ {a_{4}=\frac{\color{Cerulean}{4}\color{black}{(}\color{Cerulean}{4}\color{black}{-}1)}{2}=\frac{4(3)}{2}=\frac{12}{2}=6} \\ {a_{5}=\frac{\color{Cerulean}{5}\color{black}{(}\color{Cerulean}{5}\color{black}{-}1)}{2}=\frac{5(4)}{2}=\frac{20}{2}=10}\end{array}\)
Use \(n = 100\) to determine the \(100^{th}\) term in the sequence.
\(a_{100}=\frac{100(100-1)}{2}=\frac{100(99)}{2}=\frac{9,900}{2}=4,950\)
Answer:
First five terms: \(0, 1, 3, 6, 10\); \(a_{100} = 4,950\)
Sometimes the general term of a sequence will alternate in sign and have a variable other than \(n\).
Example \(\PageIndex{2}\):
Find the first \(5\) terms of the sequence: \(a_{n}=(-1)^{n} x^{n+1}\).
Solution:
Here we take care to replace \(n\) with the first \(5\) natural numbers and not \(x\).
\(\begin{array}{l}{a_{1}=(-1)\color{Cerulean}{^{1}}\color{black}{ x}^{\color{Cerulean}{1}\color{black}{+}1}=-x^{2}} \\ {a_{2}=(-1)^{\color{Cerulean}{2}}\color{black}{ x}^{\color{Cerulean}{2}\color{black}{+}1}=x^{3}} \\ {a_{3}=(-1)^{\color{Cerulean}{3}} \color{black}{x}^{\color{Cerulean}{3}\color{black}{+}1}=-x^{4}} \\ {a_{4}=(-1)^{\color{Cerulean}{4}}\color{black}{ x}^{\color{Cerulean}{4}\color{black}{+}1}=x^{5}} \\ {a_{5}=(-1)^{\color{Cerulean}{5}}\color{black}{ x}^{\color{Cerulean}{5}\color{black}{+}1}=-x^{6}}\end{array}\)
Answer:
\(-x^{2}, x^{3},-x^{4}, x^{5},-x^{6}\)
Exercise \(\PageIndex{1}\)
Find the first \(5\) terms of the sequence: \(a_{n}=(-1)^{n+1} 2^{n}\).
- Answer
-
\(2, −4, 8, −16, 32.\)
One interesting example is the Fibonacci sequence. The first two numbers in the Fibonacci sequence are \(1\), and each successive term is the sum of the previous two. Therefore, the general term is expressed in terms of the previous two as follows:
\(F_{n}=F_{n-2}+F_{n-1}\)
Here \(F_{1} = 1, F_{2} = 1\), and \(n > 2\). A formula that describes a sequence in terms of its previous terms is called a recurrence relation5.
Example \(\PageIndex{3}\):
Find the first \(7\) Fibonacci numbers.
Solution:
Given that \(F_{1} = 1\) and \(F_{2} = 1\), use the recurrence relation \(F_{n}=F_{n-2}+F_{n-1}\) where \(n\) is an integer starting with \(n = 3\) to find the next \(5\) terms:
\(\begin{array}{l}{F_{3}=F_{\color{Cerulean}{3}\color{black}{-}2}+F_{\color{Cerulean}{3}\color{black}{-}1}=F_{1}+F_{2}=1+1=2} \\ {F_{4}=F_{\color{Cerulean}{4}\color{black}{-}2}+F_{\color{Cerulean}{4}\color{black}{-}1}=F_{2}+F_{3}=1+2=3} \\ {F_{5}=F_{\color{Cerulean}{5}\color{black}{-}2}+F_{\color{Cerulean}{5}\color{black}{-}1}=F_{3}+F_{4}=2+3=5} \\ {F_{6}=F_{\color{Cerulean}{6}\color{black}{-}2}+F_{\color{Cerulean}{6}\color{black}{-}1}=F_{4}+F_{5}=3+5=8} \\ {F_{7}=F_{\color{Cerulean}{7}\color{black}{-}2}+F_{\color{Cerulean}{7}\color{black}{-}1}=F_{5}+F_{6}=5+8=13}\end{array}\)
Answer:
\(1,1,2,3,5,8,13\)

Figure 9.1.1: Leonardo Fibonacci (1170–1250)
Fibonacci numbers appear in applications ranging from art to computer science and biology. The beauty of this sequence can be visualized by constructing a Fibonacci spiral. Consider a tiling of squares where each side has a length that matches each Fibonacci number:
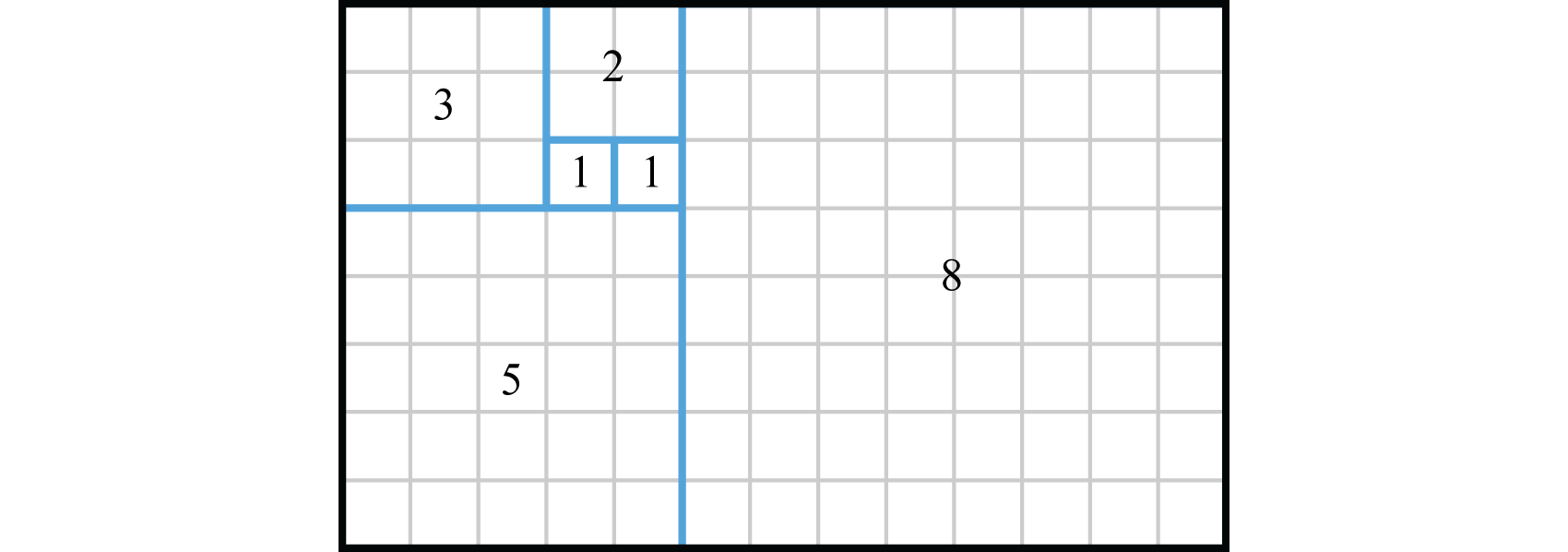
Figure 9.1.2
Connecting the opposite corners of the squares with an arc produces a special spiral shape.

Figure 9.1.3
This shape is called the Fibonacci spiral and approximates many spiral shapes found in nature.
Series
A series6 is the sum of the terms of a sequence. The sum of the terms of an infinite sequence results in an infinite series7, denoted \(S_{∞}\). The sum of the first \(n\) terms in a sequence is called a partial sum8, denoted \(S_{n}\). For example, given the sequence of positive odd integers \(1, 3, 5,…\) we can write:
\(\begin{array}{l}{S_{\infty}=1+3+5+7+9+\dots \quad\color{Cerulean} { Infinite\: series }} \\ {S_{5}=1+3+5+7+9=25 \quad\:\:\color{Cerulean} { 5th\: partial\: sum }}\end{array}\)
Example \(\PageIndex{4}\):
Determine the \(3^{rd}\) and \(5^{th}\) partial sums of the sequence: \(3,−6, 12,−24, 48,… \)
Solution:
\(S_{3}=3+(-6)+12=9\)
\(S_{5}=3+(-6)+12+(-24)+48=33\)
Answer:
\(S_{3}=9 ; S_{5}=33\)
If the general term is known, then we can express a series using sigma9 (or summation10) notation:
\(\begin{aligned}S_{\infty}&=\sum_{n=1}^{\infty} n^{2}=1^{2}+2^{2}+3^{2}+\ldots & \color{Cerulean}{Infinite\:series} \\ S_{3}&=\sum_{n=1}^{3} n^{2}=1^{2}+2^{2}+3^{2} & \color{Cerulean}{3rd\:partial\:sum}\end{aligned}\)
The symbol \(\Sigma\) (upper case Greek letter sigma) is used to indicate a series. The expressions above and below indicate the range of the index of summation11, in this case represented by \(n\). The lower number indicates the starting integer and the upper value indicates the ending integer. The \(n\)th partial sum \(S_{n}\) can be expressed using sigma notation as follows:
\(S_{n}=\sum_{k=1}^{n} a_{k}=a_{1}+a_{2}+\cdots+a_{n}\)
This is read, “the sum of \(a_{k}\) as \(k\) goes from \(1\) to \(n\).” Replace \(n\) with \(∞\) to indicate an infinite sum.
Example \(\PageIndex{5}\):
Evaluate: \(\sum_{k=1}^{5}(-3)^{n-1}\).
\(\begin{aligned} \sum_{k=1}^{5}(-3)^{k-1} &=(-3)^{\color{Cerulean}{1}\color{black}{-}1}+(-3)^{\color{Cerulean}{2}\color{black}{-}1}+(-3)^{\color{Cerulean}{3}\color{black}{-}1}+(-3)^{\color{Cerulean}{4}\color{black}{-}1}+(-3)^{\color{Cerulean}{5}\color{black}{-}1} \\ &=(-3)^{0}+(-3)^{1}+(-3)^{2}+(-3)^{3}+(-3)^{4} \\ &=1-3+9-27+81 \\ &=61 \end{aligned}\)
Answer:
\(61\)
When working with sigma notation, the index does not always start at \(1\).
Example \(\PageIndex{1}\):
Evaluate: \(\sum_{k=2}^{5}(-1)^{k}(3 k)\)
Solution:
Here the index is expressed using the variable \(k\), which ranges from \(2\) to \(5\).
Exercise \(\PageIndex{2}\)
Evaluate: \(\sum_{n=1}^{5}(15-9 n)\).
- Answer
-
\(-60\)
Infinity is used as the upper bound of a sum to indicate an infinite series.
Example \(\PageIndex{7}\):
Write in expanded form: \(\sum_{i=0}^{\infty} \frac{n}{n+1}\).
Solution:
In this case we begin with \(n = 0\) and add three dots to indicate that this series continues forever.
\(\begin{aligned} \sum_{n=0}^{\infty} \frac{n}{n+1} &=\frac{\color{Cerulean}{0}}{\color{Cerulean}{0}\color{black}{+}1}+\frac{\color{Cerulean}{1}}{\color{Cerulean}{1}\color{black}{+}1}+\frac{\color{Cerulean}{2}}{\color{Cerulean}{2}\color{black}{+}1}+\frac{\color{Cerulean}{3}}{\color{Cerulean}{3}\color{black}{+}1}+\cdots \\ &=\frac{0}{1}+\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots \\ &=0+\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots \end{aligned}\)
Answer:
\(0+\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots\)
When expanding a series, take care to replace only the variable indicated by the index.
Example \(\PageIndex{8}\):
Write in expanded form: \(\sum_{i=1}^{\infty}(-1)^{i-1} x^{2 i}\).
Solution:
\(\begin{aligned} \sum_{i=1}^{\infty}(-1)^{i-1} x^{2 i} &=(-1)^{\color{Cerulean}{1}\color{black}{-}1} x^{2(\color{Cerulean}{1}\color{black}{)}}+(-1)^{\color{Cerulean}{2}\color{black}{-}1} x^{2(\color{Cerulean}{2}\color{black}{)}}+(-1)^{\color{Cerulean}{3}\color{black}{-}1} x^{2(\color{Cerulean}{3}\color{black}{)}}+\cdots \\ &=(-1)^{0} x^{2(1)}+(-1)^{1} x^{2(2)}+(-1)^{2} x^{2(3)}+\cdots \\ &=x^{2}-x^{4}+x^{6}-\cdots \end{aligned}\)
Answer:
\(x^{2}-x^{4}+x^{6}-\cdots\)
Key Takeaways
- A sequence is a function whose domain consists of a set of natural numbers beginning with \(1\). In addition, a sequence can be thought of as an ordered list.
- Formulas are often used to describe the \(n\)th term, or general term, of a sequence using the subscripted notation \(a_{n}\).
- A series is the sum of the terms in a sequence. The sum of the first \(n\) terms is called the \(n\)th partial sum and is denoted \(S_{n}\).
- Use sigma notation to denote summations in a compact manner. The nth partial sum, using sigma notation, can be written \(S_{n}=\sum_{k=1}^{n} a_{k}\). The symbol \(\Sigma\) denotes a summation where the expression below indicates that the index \(k\) starts at \(1\) and iterates through the natural numbers ending with the value \(n\) above.
Exercise \(\PageIndex{3}\)
Find the first \(5\) terms of the sequence as well as the \(30^{th}\) term.
- \(a_{n}=2 n\)
- \(a_{n}=2 n+1\)
- \(a_{n}=\frac{n^{2}-1}{2}\)
- \(a_{n}=\frac{n}{2 n-1}\)
- \(a_{n}=(-1)^{n}(n+1)^{2}\)
- \(a_{n}=(-1)^{n+1} n^{2}\)
- \(a_{n}=3^{n-1}\)
- \(a_{n}=2^{n-2}\)
- \(a_{n}=\left(\frac{1}{2}\right)^{n}\)
- \(a_{n}=\left(-\frac{1}{3}\right)^{n}\)
- \(a_{n}=\frac{(-1)^{n-1}}{3 n-1}\)
- \(a_{n}=\frac{2(-1)^{n}}{n+5}\)
- \(a_{n}=1+\frac{1}{n}\)
- \(a_{n}=\frac{n^{2}+1}{n}\)
- Answer
-
1. \(2,4,6,8,10 ; a_{30}=60\)
3. \(0, \frac{3}{2}, 4, \frac{15}{2}, 12 ; a_{30}=\frac{899}{2}\)
5. \(-4,9,-16,25,-36 ; a_{30}=961\)
7. \(1,3,9,27,81 ; a_{30}=3^{29}\)
9. \(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32} ; a_{30}=\frac{1}{2^{30}}\)
11. \(\frac{1}{2},-\frac{1}{5}, \frac{1}{8},-\frac{1}{11}, \frac{1}{14} ; a_{30}=-\frac{1}{89}\)
13. \(2, \frac{3}{2}, \frac{4}{3}, \frac{5}{4}, \frac{6}{5} ; a_{30}=\frac{31}{30}\)
Exercise \(\PageIndex{4}\)
Find the first \(5\) terms of the sequence.
- \(a_{n}=2 x^{2 n-1}\)
- \(a_{n}=(2 x)^{n-1}\)
- \(a_{n}=\frac{x^{n}}{n+4}\)
- \(a_{n}=\frac{x^{2 n}}{x-2}\)
- \(a_{n}=\frac{n x^{2 n}}{n+1}\)
- \(a_{n}=\frac{(n+1) x^{n}}{n^{2}}\)
- \(a_{n}=(-1)^{n} x^{3 n}\)
- \(a_{n}=(-1)^{n-1} x^{n+1}\)
- Answer
-
1. \(2 x, 2 x^{3}, 2 x^{5}, 2 x^{7}, 2 x^{9}\)
3. \(\frac{x}{5}, \frac{x^{2}}{6}, \frac{x^{3}}{7}, \frac{x^{4}}{8}, \frac{x^{5}}{9}\)
5. \(\frac{x^{2}}{2}, \frac{2 x^{4}}{3}, \frac{3 x^{6}}{4}, \frac{4 x^{8}}{5}, \frac{5 x^{10}}{6}\)
7. \(-x^{3}, x^{6},-x^{9}, x^{12},-x^{15}\)
Exercise \(\PageIndex{5}\)
Find the first 5 terms of the sequence defined by the given recurrence relation.
- \(a_{n}=a_{n-1}+5\) where \(a_{1}=3\)
- \(a_{n}=a_{n-1}-3\) where \(a_{1}=4\)
- \(a_{n}=3 a_{n-1}\) where \(a_{1}=-2\)
- \(a_{n}=-2 a_{n-1}\) where \(a_{1}=-1\)
- \(a_{n}=n a_{n-1}\) where \(a_{1}=1\)
- \(a_{n}=(n-1) a_{n-1}\) where \(a_{1}=1\)
- \(a_{n}=2 a_{n-1}-1\) where \(a_{1}=0\)
- \(a_{n}=3 a_{n-1}+1\) where \(a_{1}=-1\)
- \(a_{n}=a_{n-2}+2 a_{n-1}\) where \(a_{1}=-1\) and \(a_{2}=0\)
- \(a_{n}=3 a_{n-1}-a_{n-2}\) where \(a_{1}=0\) and \(a_{2}=2\)
- \(a_{n}=a_{n-1}-a_{n-2}\) where \(a_{1}=1\) and \(a_{2}=3\)
- \(a_{n}=a_{n-2}+a_{n-1}+2\) where \(a_{1}=-4\) and \(a_{2}=-1\)
- Answer
-
1. \(3, 8, 13, 18, 23\)
3. \(−2, −6, −18, −54, −162\)
5. \(1, 2, 6, 24, 120\)
7. \(0, −1, −3, −7, −15\)
9. \(−1, 0, −1, −2, −5\)
11. \(1, 3, 2, −1, −3\)
Exercise \(\PageIndex{6}\)
Find the indicated term.
- \(a_{n}=2-7 n ; a_{12}\)
- \(a_{n}=3 n-8 ; a_{20}\)
- \(a_{n}=-4(5)^{n-4} ; a_{7}\)
- \(a_{n}=6\left(\frac{1}{3}\right)^{n-6} ; a_{9}\)
- \(a_{n}=1+\frac{1}{n}; a_{10}\)
- \(a_{n}=(n+1) 5^{n-3} ; a_{5}\)
- \(a_{n}=(-1)^{n} 2^{2 n-3} ; a_{4}\)
- \(a_{n}=n(n-1)(n-2) ; a_{6}\)
- An investment of $\(4,500\) is made in an account earning \(2\)% interest compounded quarterly. The balance in the account after \(n\) quarters is given by \(a_{n}=4500\left(1+\frac{0.02}{4}\right)^{n}\). Find the amount in the account after each quarter for the first two years. Round to the nearest cent.
- The value of a new car after \(n\) years is given by the formula \(a_{n}=18,000\left(\frac{3}{4}\right)^{n}\). Find and interpret \(a_{7}\). Round to the nearest whole dollar.
- The number of comparisons a computer algorithm makes to sort n names in a list is given by the formula \(a_{n}=n \log _{2} n\). Determine the number of comparisons it takes this algorithm to sort \(2 × 10^{6}\) (2 million) names.
- The number of comparisons a computer algorithm makes to search \(n\) names in a list is given by the formula \(a_{n}=n^{2}\) Determine the number of comparisons it takes this algorithm to search \(2 × 10^{6}\) (2 million) names.
- Answer
-
1. \(-82\)
3. \(-500\)
5. \(\frac{11}{10}\)
7. \(32\)
9. Year 1: QI: $\(4,522.50\); QII: $\(4,545.11\); QIII: $\(4,567.84\); QIV: $\(4,590.68\); Year 2: QI: $\(4,613.63\); QII: $\(4,636.70\); QIII: $\(4,659.88\); QIV: $\(4,683.18\)
11. Approximately \(4 \times 10^{7}\) comparisons
Exercise \(\PageIndex{7}\)
Find the indicated partial sum.
- \(3,5,9,17,33, \ldots ; S_{4}\)
- \(-5,7,-29,79,-245, \ldots ; S_{4}\)
- \(4,1,-4,-11,-20, \ldots ; S_{5}\)
- \(0,2,6,12,20, \ldots ; S_{3}\)
- \(a_{n}=2-7 n ; S_{5}\)
- \(a_{n}=3 n-8 ; S_{5}\)
- \(a_{n}=-4(5)^{n-4} ; S_{3}\)
- \(a_{n}=6\left(\frac{1}{3}\right)^{n-6} ; S_{3}\)
- \(a_{n}=1+\frac{1}{n}; S_{4}\)
- \(a_{n}=(n+1) 5^{n-3} ; S_{3}\)
- \(a_{n}=(-1)^{n} 2^{2 n-3} ; S_{5}\)
- \(a_{n}=n(n-1)(n-2) ; S_{4}\)
- Answer
-
1. \(34\)
3. \(-30\)
5. \(-95\)
7. \(-\frac{124}{125}\)
9. \(\frac{73}{12}\)
11. \(-\frac{205}{2}\)
Exercise \(\PageIndex{8}\)
Evaluate.
- \(\sum_{k=1}^{5} 3 k\)
- \(\sum_{k=1}^{6} 2 k\)
- \(\sum_{i=2}^{6} i^{2}\)
- \(\sum_{i=0}^{4}(i+1)^{2}\)
- \(\sum_{n=1}^{5}(-1)^{n+1} 2^{n}\)
- \(\sum_{n=5}^{10}(-1)^{n} n^{2}\)
- \(\sum_{k=-2}^{2}\left(\frac{1}{2}\right)^{k}\)
- \(\sum_{k=-4}^{0}\left(\frac{1}{3}\right)^{k}\)
- \(\sum_{k=0}^{4}(-2)^{k+1}\)
- \(\sum_{k=-1}^{3}(-3)^{k-1}\)
- \(\sum_{n=1}^{5} 3\)
- \(\sum_{n=1}^{7}-5\)
- \(\sum_{k=-2}^{3} k(k+1)\)
- \(\sum_{k=-2}^{2}(k-2)(k+2)\)
- Answer
-
1. \(45\)
3. \(90\)
5. \(22\)
7. \(\frac{31}{4}\)
9. \(−22\)
11. \(15\)
13. \(22\)
Exercise \(\PageIndex{9}\)
Write in expanded form.
- \(\sum_{n=1}^{\infty} \frac{n-1}{n}\)
- \(\sum_{n=1}^{\infty} \frac{n}{2 n-1}\)
- \(\sum_{n=1}^{\infty}\left(-\frac{1}{2}\right)^{n-1}\)
- \(\sum_{n=0}^{\infty}\left(-\frac{2}{3}\right)^{n+1}\)
- \(\sum_{n=1}^{\infty} 3\left(\frac{1}{5}\right)^{n}\)
- \(\sum_{n=0}^{\infty} 2\left(\frac{1}{3}\right)^{n}\)
- \(\sum_{k=0}^{\infty}(-1)^{k} x^{k+1}\)
- \(\sum_{k=1}^{\infty}(-1)^{k+1} x^{k-1}\)
- \(\sum_{i=0}^{\infty}(-2)^{i+1} x^{i}\)
- \(\sum_{i=1}^{\infty}(-3)^{i-1} x^{3 i}\)
- \(\sum_{k=1}^{\infty}(2 k-1) x^{2 k}\)
- \(\sum_{k=1}^{\infty} \frac{k x^{k-1}}{k+1}\)
- Answer
-
1. \(0+\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots\)
3. \(1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\cdots\)
5. \(\frac{3}{5}+\frac{3}{25}+\frac{3}{125}+\frac{3}{625}+\cdots\)
7. \(x-x^{2}+x^{3}-x^{4}+\cdots\)
9. \(-2+4 x-8 x^{2}+16 x^{3}-\dots\)
11. \(x^{2}+3 x^{4}+5 x^{6}+7 x^{8}+\cdots\)
Exercise \(\PageIndex{10}\)
Express the following series using sigma notation.
- \(x+2 x^{2}+3 x^{3}+4 x^{4}+5 x^{5}\)
- \(\frac{1}{2} x^{2}+\frac{2}{3} x^{3}+\frac{3}{4} x^{4}+\frac{4}{5} x^{5}+\frac{5}{6} x^{6}\)
- \(2+2^{2} x+2^{3} x^{2}+2^{4} x^{3}+2^{5} x^{4}\)
- \(3 x+3^{2} x^{2}+3^{3} x^{3}+3^{4} x^{4}+3^{5} x^{5}\)
- \(2 x+4 x^{2}+8 x^{3}+\dots+2^{n} x^{n}\)
- \(x+3 x^{2}+9 x^{3}+\dots+3^{n} x^{n+1}\)
- \(5+(5+d)+(5+2 d)+\dots+(5+n d)\)
- \(2+2 r^{1}+2 r^{2}+\dots+2 r^{n-1}\)
- \(\frac{3}{4}+\frac{3}{8}+\frac{3}{16}+\dots+3\left(\frac{1}{2}\right)^{n}\)
- \(\frac{8}{3}+\frac{16}{4}+\frac{32}{5}+\dots+\frac{2^{n}}{n}\)
- A structured settlement yields an amount in dollars each year, represented by \(n\), according to the formula \(p_{n}=10,000(0.70)^{n-1}\). What is the total amount gained from the settlement after \(5\) years?
- The first row of seating in a small theater consists of \(14\) seats. Each row thereafter consists of \(2\) more seats than the previous row. If there are \(7\) rows, how many total seats are in the theater?
- Answer
-
1. \(\sum_{k=1}^{5} k x^{k}\)
3. \(\sum_{k=1}^{5} 2^{k} x^{k-1}\)
5. \(\sum_{k=1}^{n} 2^{k} x^{k}\)
7. \(\sum_{k=0}^{n}(5+k d)\)
9. \(\sum_{k=2}^{n} 3\left(\frac{1}{2}\right)^{k}\)
11. \(\$ 27,731\)
Exercise \(\PageIndex{11}\)
- Research and discuss Fibonacci numbers as they are found in nature.
- Research and discuss the life and contributions of Leonardo Fibonacci.
- Explain the difference between a sequence and a series. Provide an example of each.
- Answer
-
1. Answer may vary
3. Answer may vary
Footnotes
1A function whose domain is a set of consecutive natural numbers starting with \(1\).
2A sequence whose domain is the set of natural numbers \(\{1,2,3, \dots\}\).
3An equation that defines the nth term of a sequence commonly denoted using subscripts \(a_{n}\).
4A sequence whose domain is \(\{1,2,3, \dots, k\}\) where \(k\) is a natural number.
5A formula that uses previous terms of a sequence to describe subsequent terms.
6The sum of the terms of a sequence.
7The sum of the terms of an infinite sequence denoted \(S_{∞}\).
8The sum of the first n terms in a sequence denoted \(S_{n}\).
9A sum denoted using the symbol \(\Sigma\) (upper case Greek letter sigma).
10Used when referring to sigma notation.
11The variable used in sigma notation to indicate the lower and upper bounds of the summation.


