1.5: Factoring Polynomials

Learning Objectives

In this section students will:

• Factor the greatest common factor of a polynomial.
• Factor a trinomial.
• Factor by grouping.
• Factor a perfect square trinomial.
• Factor a difference of squares.
• Factor the sum and difference of cubes.
• Factor expressions using fractional or negative exponents.

Imagine that we are trying to find the area of a lawn so that we can determine how much grass seed to purchase. The lawn is the green portion in Figure $\PageIndex{1}$.

Figure $\PageIndex{1}$

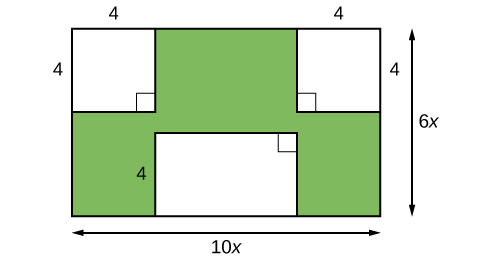
The area of the entire region can be found using the formula for the area of a rectangle.

$$\begin{align*} A &= lw\\ &= 10x\times6x\\ &= 60x^2\; units^2 \end{align*}$$

The areas of the portions that do not require grass seed need to be subtracted from the area of the entire region. The two square regions each have an area of $A =s^2=4^2= 16\; units^2$. The other rectangular region has one side of length $10x−8$ and one side of length $4$, giving an area of

$$A =lw=4(10x−8)=40x−32\; \text{units}^2. \nonumber$$

So the region that must be subtracted has an area of

$$2(16)+40x−32= 40x\; \text{units}^2. \nonumber$$

The area of the region that requires grass seed is found by subtracting $60x^2−40x\; \text{units}^2$. This area can also be expressed in factored form as $20x (3x−2)\; \text{units}^2$. We can confirm that this is an equivalent expression by multiplying.

Many polynomial expressions can be written in simpler forms by factoring. In this section, we will look at a variety of methods that can be used to factor polynomial expressions.

Factoring the Greatest Common Factor of a Polynomial

When we study fractions, we learn that the greatest common factor (GCF) of two numbers is the largest number that divides evenly into both numbers. For instance, $4$ is the GCF of $16$ and $20$ because it is the largest number that divides evenly into both $16$ and $20$ The GCF of polynomials works the same way: $4x$ is the GCF of $16x$ and $20x^2$ because it is the largest polynomial that divides evenly into both $16x$ and $20x^2$.

When factoring a polynomial expression, our first step should be to check for a GCF. Look for the GCF of the coefficients, and then look for the GCF of the variables.

Definition: Greatest Common Factor

The greatest common factor (GCF) of polynomials is the largest polynomial that divides evenly into the polynomials.

Howto: Given a polynomial expression, factor out the greatest common factor

1. Identify the GCF of the coefficients.
2. Identify the GCF of the variables.
3. Combine to find the GCF of the expression.
4. Determine what the GCF needs to be multiplied by to obtain each term in the expression.
5. Write the factored expression as the product of the GCF and the sum of the terms we need to multiply by.

Example $\PageIndex{1}$: Factoring the Greatest Common Factor

Factor $6x^3y^3 +45x^2y^2+21xy$.

Solution

First, find the GCF of the expression. The GCF of $6$, $45$, and $21$ is $3$. The GCF of $x^3$,$x^2$, and $x$ is $x$. (Note that the GCF of a set of expressions in the form $x^n$ will always be the exponent of lowest degree.) And the GCF of $y^3$,$y^2$, and $y$ is $y$. Combine these to find the GCF of the polynomial, $3xy$.

Next, determine what the GCF needs to be multiplied by to obtain each term of the polynomial. We find that

• $3xy(2x^2y^2)=6x^3y^3$,
• $3xy(15xy)=45x^2y^2$, and
• $3xy(7)=21xy$.

Finally, write the factored expression as the product of the GCF and the sum of the terms we needed to multiply by.

$$(3xy)(2x^2y^2+15xy+7) \nonumber$$

Analysis

After factoring, we can check our work by multiplying. Use the distributive property to confirm that

$$(3xy)(2x^2y^2+15xy+7)=6x^3y^3+45x^2y^2+21xy \nonumber$$

Exercise $\PageIndex{1}$

Factor $x(b^2−a)+6(b^2−a)$ by pulling out the GCF.

Answer

$(b^2−a)(x+6)$

Factoring a Trinomial with Leading Coefficient 1

Although we should always begin by looking for a GCF, pulling out the GCF is not the only way that polynomial expressions can be factored. The polynomial $x^2+5x+6$ has a GCF of $1$, but it can be written as the product of the factors $(x+2)$ and $(x+3)$.

Trinomials of the form $x^2+bx+c$ can be factored by finding two numbers with a product of $c$ and a sum of $b$. The trinomial $x^2+10x+16$, for example, can be factored using the numbers $2$ and $8$ because the product of those numbers is $16$ and their sum is $10$. The trinomial can be rewritten as the product of $(x+2)$ and $(x+8)$.

FACTORING A TRINOMIAL WITH LEADING COEFFICIENT $1$

A trinomial of the form $x^2+bx+c$ can be written in factored form as $(x+p)(x+q)$ where $pq=c$ and $p+q=b$.

Q&A: Can every trinomial be factored as a product of binomials?

No. Some polynomials cannot be factored. These polynomials are said to be prime.

Howto: Given a trinomial in the form $x^2+bx+c$, factor it

1. List factors of $c$.
2. Find $p$ and $q$, a pair of factors of $c$ with a sum of $b$.
3. Write the factored expression $(x+p)(x+q)$.

Example $\PageIndex{2}$: Factoring a Trinomial with Leading Coefficient 1

Factor $x^2+2x−15$.

Solution

We have a trinomial with leading coefficient $1$, $b=2$, and $c=−15$. We need to find two numbers with a product of $−15$ and a sum of $2$. In Table $\PageIndex{1}$, we list factors until we find a pair with the desired sum.

Table $\PageIndex{1}$

Factors of −15	Sum of Factors
1,−15	−14
−1,15	14
3,−5	−2
−3,5

Now that we have identified $p$ and $q$ as $−3$ and $5$, write the factored form as $(x−3)(x+5)$.

Analysis

We can check our work by multiplying. Use FOIL to confirm that $(x−3)(x+5)=x^2+2x−15$.

Q&A: Does the order of the factors matter?

No. Multiplication is commutative, so the order of the factors does not matter.

Exercise $\PageIndex{2}$

Factor $x^2−7x+6$.

Answer

$(x−6)(x−1)$

Factoring by Grouping

Trinomials with leading coefficients other than $1$ are slightly more complicated to factor. For these trinomials, we can factor by grouping by dividing the x term into the sum of two terms, factoring each portion of the expression separately, and then factoring out the GCF of the entire expression. The trinomial $2x^2+5x+3$ can be rewritten as $(2x+3)(x+1)$ using this process. We begin by rewriting the original expression as $2x^2+2x+3x+3$ and then factor each portion of the expression to obtain $2x(x+1)+3(x+1)$. We then pull out the GCF of $(x+1)$ to find the factored expression.

Factor by Grouping

To factor a trinomial in the form $ax^2+bx+c$ by grouping, we find two numbers with a product of $ac$ and a sum of $b$. We use these numbers to divide the $x$ term into the sum of two terms and factor each portion of the expression separately, then factor out the GCF of the entire expression.

Howto: Given a trinomial in the form $ax^2+bx+c$, factor by grouping.

1. List factors of $ac$.
2. Find $p$ and $q$, a pair of factors of $ac$ with a sum of $b$.
3. Rewrite the original expression as $ax^2+px+qx+c$.
4. Pull out the GCF of $ax^2+px$.
5. Pull out the GCF of $qx+c$.
6. Factor out the GCF of the expression.

Example $\PageIndex{3}$: Factoring a Trinomial by Grouping

Factor $5x^2+7x−6$ by grouping.

Solution

We have a trinomial with $a=5$, $b=7$, and $c=−6$. First, determine $ac=−30$. We need to find two numbers with a product of $−30$ and a sum of $7$. In the table below, we list factors until we find a pair with the desired sum.

Table $\PageIndex{2}$

Factors of −30	Sum of Factors
1,−30	−29
−1,30	29
2,−15	−13
−2,15	13
3,−10	−7
−3,10	7

So $p=−3$ and $q=10$.

$5x^2−3x+10x−6$ Rewrite the original expression as $ax^2+px+qx+c$.

$x(5x−3)+2(5x−3)$ Factor out the GCF of each part

$(5x−3)(x+2)$ Factor out the GCF of the expression.

Analysis

We can check our work by multiplying. Use FOIL to confirm that $(5x−3)(x+2)=5x^2+7x−6$.

Exercise $\PageIndex{3}$

Factor:

1. $2x^2+9x+9$
2. $6x^2+x−1$

Answer a

$(2x+3)(x+3)$

Answer b

$(3x-1)(2x+1)$

Factoring a Perfect Square Trinomial

A perfect square trinomial is a trinomial that can be written as the square of a binomial. Recall that when a binomial is squared, the result is the square of the first term added to twice the product of the two terms and the square of the last term.

$$a^2+2ab+b^2={(a+b)}^2$$

and

$$a^2-2ab+b^2={(a-b)}^2$$

We can use this equation to factor any perfect square trinomial.

Perfect Square Trinomials

A perfect square trinomial can be written as the square of a binomial:

$$a^2+2ab+b^2=(a+b)^2$$

Howto: Given a perfect square trinomial, factor it into the square of a binomial

1. Confirm that the first and last term are perfect squares.
2. Confirm that the middle term is twice the product of $ab$.
3. Write the factored form as ${(a+b)}^2$.

Example $\PageIndex{4}$: Factoring a Perfect Square Trinomial

Factor $25x^2+20x+4$.

Solution

Notice that $25x^2$ and $4$ are perfect squares because $25x^2={(5x)}^2$ and $4=2^2$. Then check to see if the middle term is twice the product of $5x$ and $2$. The middle term is, indeed, twice the product: $2(5x)(2)=20x$. Therefore, the trinomial is a perfect square trinomial and can be written as ${(5x+2)}^2$.

Exercise $\PageIndex{4}$

Factor $49x^2−14x+1$.

Answer

${(7x−1)}^2$

Factoring a Difference of Squares

A difference of squares is a perfect square subtracted from a perfect square. Recall that a difference of squares can be rewritten as factors containing the same terms but opposite signs because the middle terms cancel each other out when the two factors are multiplied.

$$a^2−b^2=(a+b)(a−b)$$

We can use this equation to factor any differences of squares.

Differences of Squares

A difference of squares can be rewritten as two factors containing the same terms but opposite signs.

$$a^2−b^2=(a+b)(a−b)$$

Howto: Given a difference of squares, factor it into binomials

1. Confirm that the first and last term are perfect squares.
2. Write the factored form as $(a+b)(a−b)$.

Example $\PageIndex{5}$: Factoring a Difference of Squares

Factor $9x^2−25$.

Solution

Notice that $9x^2$ and $25$ are perfect squares because $9x^2={(3x)}^2$ and $25=5^2$. The polynomial represents a difference of squares and can be rewritten as $(3x+5)(3x−5)$.

Exercise $\PageIndex{5}$

Factor $81y^2−100$.

Answer

$(9y+10)(9y−10)$

Q&A: Is there a formula to factor the sum of squares?

No. A sum of squares cannot be factored.

Factoring the Sum and Difference of Cubes

Now, we will look at two new special products: the sum and difference of cubes. Although the sum of squares cannot be factored, the sum of cubes can be factored into a binomial and a trinomial.

$$a^3+b^3=(a+b)(a^2−ab+b^2)$$

Similarly, the sum of cubes can be factored into a binomial and a trinomial, but with different signs.

$$a^3−b^3=(a−b)(a^2+ab+b^2)$$

We can use the acronym SOAP to remember the signs when factoring the sum or difference of cubes. The first letter of each word relates to the signs: Same Opposite Always Positive. For example, consider the following example.

$$x^3−2^3=(x−2)(x^2+2x+4)$$

The sign of the first 2 is the same as the sign between $x^3−2^3$. The sign of the $2x$ term is opposite the sign between $x^3−2^3$. And the sign of the last term, $4$, is always positive.

Sum and Difference of Cubes

We can factor the sum of two cubes as

$$a^3+b^3=(a+b)(a^2−ab+b^2)$$

We can factor the difference of two cubes as

$$a^3−b^3=(a−b)(a^2+ab+b^2)$$

Howto: Given a sum of cubes or difference of cubes, factor it

1. Confirm that the first and last term are cubes, $a^3+b^3$ or $a^3−b^3$.
2. For a sum of cubes, write the factored form as $(a+b)(a^2−ab+b^2)$. For a difference of cubes, write the factored form as $(a−b)(a^2+ab+b^2)$.

Example $\PageIndex{6}$: Factoring a Sum of Cubes

Factor $x^3+512$.

Solution

Notice that $x^3$ and $512$ are cubes because $8^3=512$. Rewrite the sum of cubes as $(x+8)(x^2−8x+64)$.

Analysis

After writing the sum of cubes this way, we might think we should check to see if the trinomial portion can be factored further. However, the trinomial portion cannot be factored, so we do not need to check.

Exercise $\PageIndex{6}$

Factor the sum of cubes: $216a^3+b^3$.

Answer

$(6a+b)(36a^2−6ab+b^2)$

Example $\PageIndex{7}$: Factoring a Difference of Cubes

Factor $8x^3−125$.

Solution

Notice that $8x^3$ and $125$ are cubes because $8x^3={(2x)}^3$ and $125=5^3$. Write the difference of cubes as $(2x−5)(4x^2+10x+25)$.

Analysis

Just as with the sum of cubes, we will not be able to further factor the trinomial portion.

Exercise $\PageIndex{7}$

Factor the difference of cubes: $1000x^3−1$

Answer

$(10x−1)(100x^2+10x+1)$

Factoring Expressions with Fractional or Negative Exponents

Expressions with fractional or negative exponents can be factored by pulling out a GCF. Look for the variable or exponent that is common to each term of the expression and pull out that variable or exponent raised to the lowest power. These expressions follow the same factoring rules as those with integer exponents. For instance, $2x^{\tfrac{1}{4}}+5x^{\tfrac{3}{4}}$ can be factored by pulling out $x^{\tfrac{1}{4}}$ and being rewritten as $x^{\tfrac{1}{4}}(2+5x^{\tfrac{1}{2}})$.

Example $\PageIndex{8}$: Factoring an Expression with Fractional or Negative Exponents

Factor $3x{(x+2)}^{-\tfrac{1}{3}}+4{(x+2)}^{\tfrac{2}{3}}$.

Solution

Factor out the term with the lowest value of the exponent. In this case, that would be ${(x+2)}^{-\tfrac{1}{3}}$.

$$\begin{align*} &(x+2)^{-\tfrac{1}{3}}(3x+4(x+2))\qquad \text{Factor out the GCF }\\ &(x+2)^{-\tfrac{1}{3}}(3x+4x+8)\qquad \text{Simplify } \\ &(x+2)^{-\tfrac{1}{3}}(7x+8) \end{align*}$$

Exercise $\PageIndex{8}$

Factor $2{(5a−1)}^{\tfrac{3}{4}}+7a{(5a−1)}^{−\tfrac{1}{4}}$.

Answer

${(5a−1)}^{−\tfrac{1}{4}}(17a−2)$

Media

Access these online resources for additional instruction and practice with factoring polynomials.

1. Identify GCF

2. Factor Trinomials when a Equals 1

3. Factor Trinomials when a is not equal to 1

4. Factor Sum or Difference of Cubes

Key Equations

difference of squares	$a^2−b^2=(a+b)(a−b)$
perfect square trinomial	$a^2+2ab+b^2=(a+b)^2$
sum of cubes	$a^3+b^3=(a+b)(a^2−ab+b^2)$
difference of cubes	$a^3−b^3=(a−b)(a^2+ab+b^2)$

• The greatest common factor, or GCF, can be factored out of a polynomial. Checking for a GCF should be the first step in any factoring problem. See Example.
• Trinomials with leading coefficient 1 can be factored by finding numbers that have a product of the third term and a sum of the second term. See Example.
• Trinomials can be factored using a process called factoring by grouping. See Example.
• Perfect square trinomials and the difference of squares are special products and can be factored using equations. See Example and Example.
• The sum of cubes and the difference of cubes can be factored using equations. See Example and Example.
• Polynomials containing fractional and negative exponents can be factored by pulling out a GCF. See Example.