2.2: Linear Equations in One Variable
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Solve equations in one variable algebraically.
- Solve a rational equation.
- Find a linear equation.
- Given the equations of two lines, determine whether their graphs are parallel or perpendicular.
- Write the equation of a line parallel or perpendicular to a given line.
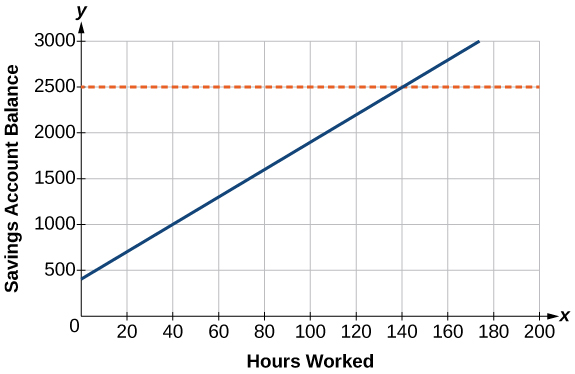
Caroline is a full-time college student planning a spring break vacation. To earn enough money for the trip, she has taken a part-time job at the local bank that pays
Solving Linear Equations in One Variable
A linear equation is an equation of a straight line, written in one variable. The only power of the variable is
- An identity equation is true for all values of the variable. Here is an example of an identity equation:
- A conditional equation is true for only some values of the variable. For example, if we are to solve the equation
- An inconsistent equation results in a false statement. For example, if we are to solve
Solving linear equations in one variable involves the fundamental properties of equality and basic algebraic operations. A brief review of those operations follows.
A linear equation in one variable can be written in the form
where a and b are real numbers,
The following steps are used to manipulate an equation and isolate the unknown variable, so that the last line reads
- We may add, subtract, multiply, or divide an equation by a number or an expression as long as we do the same thing to both sides of the equal sign. Note that we cannot divide by zero.
- Apply the distributive property as needed:
- Isolate the variable on one side of the equation.
- When the variable is multiplied by a coefficient in the final stage, multiply both sides of the equation by the reciprocal of the coefficient.
Solve the following equation:
Solution
This equation can be written in the form
The solution is
Solve the linear equation in one variable:
- Answer
-
Solve the following equation:
Solution
Apply standard algebraic properties.
Analysis
This problem requires the distributive property to be applied twice, and then the properties of algebra are used to reach the final line,
Solve the equation in one variable:
- Answer
-
Solving a Rational Equation
In this section, we look at rational equations that, after some manipulation, result in a linear equation. If an equation contains at least one rational expression, it is a considered a rational equation. Recall that a rational number is the ratio of two numbers, such as
or
Rational equations have a variable in the denominator in at least one of the terms. Our goal is to perform algebraic operations so that the variables appear in the numerator. In fact, we will eliminate all denominators by multiplying both sides of the equation by the least common denominator (LCD). Finding the LCD is identifying an expression that contains the highest power of all of the factors in all of the denominators. We do this because when the equation is multiplied by the LCD, the common factors in the LCD and in each denominator will equal one and will cancel out.
Solve the rational equation:
Solution
We have three denominators;
A common mistake made when solving rational equations involves finding the LCD when one of the denominators is a binomial—two terms added or subtracted—such as
So, both sides of the equation would be multiplied by
Another example is a problem with two denominators, such as
Sometimes we have a rational equation in the form of a proportion; that is, when one fraction equals another fraction and there are no other terms in the equation.
We can use another method of solving the equation without finding the LCD: cross-multiplication. We multiply terms by crossing over the equal sign.
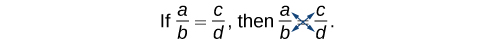
Multiply a(d) and b(c), which results in
Any solution that makes a denominator in the original expression equal zero must be excluded from the possibilities.
A rational equation contains at least one rational expression where the variable appears in at least one of the denominators.
- Factor all denominators in the equation.
- Find and exclude values that set each denominator equal to zero.
- Find the LCD.
- Multiply the whole equation by the LCD. If the LCD is correct, there will be no denominators left.
- Solve the remaining equation.
- Make sure to check solutions back in the original equations to avoid a solution producing zero in a denominator
Solve the following rational equation:
We have three denominators:
The proposed solution is
Solve the rational equation:
- Answer
-
Solve the following rational equation:
Solution
First find the common denominator. The three denominators in factored form are
The solution is
Solve the rational equation:
- Answer
-
Solve the following rational equations and state the excluded values:
Solution
a.
The denominators
The solution is
b.
The LCD is
The solution is
c.
The least common denominator is
The solution is
Solve
- Answer
-
Solve the rational equation after factoring the denominators:
Solution
We must factor the denominator
The solution is
Solve the rational equation:
- Answer
-
Finding a Linear Equation
Perhaps the most familiar form of a linear equation is the slope-intercept form, written as
The slope of a line refers to the ratio of the vertical change in
If the slope is positive, the line slants to the right. If the slope is negative, the line slants to the left. As the slope increases, the line becomes steeper. Some examples are shown in Figure
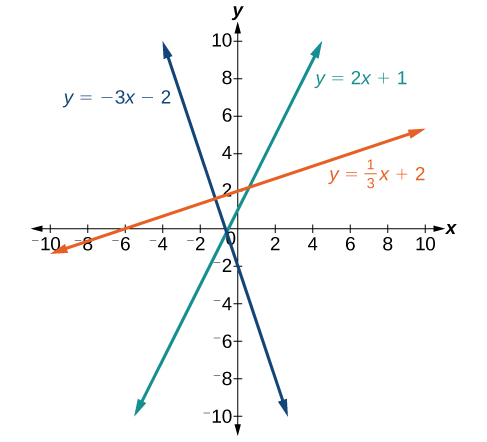
The slope of a line,
Find the slope of a line that passes through the points
Solution
We substitute the
The slope is
Analysis
It does not matter which point is called
Find the slope of the line that passes through the points
- Answer
-
Identify the slope and
Solution
As the line is in
Analysis
The
The Point-Slope Formula
Given the slope and one point on a line, we can find the equation of the line using the point-slope formula.
This is an important formula, as it will be used in other areas of college algebra and often in calculus to find the equation of a tangent line. We need only one point and the slope of the line to use the formula. After substituting the slope and the coordinates of one point into the formula, we simplify it and write it in slope-intercept form.
Given one point and the slope, the point-slope formula will lead to the equation of a line:
Write the equation of the line with slope
Solution
Using the point-slope formula, substitute
Analysis
Note that any point on the line can be used to find the equation. If done correctly, the same final equation will be obtained.
Given
- Answer
-
Find the equation of the line passing through the points
Solution
First, we calculate the slope using the slope formula and two points.
Next, we use the point-slope formula with the slope of
In slope-intercept form, the equation is written as
Analysis
To prove that either point can be used, let us use the second point
We see that the same line will be obtained using either point. This makes sense because we used both points to calculate the slope.
Standard Form of a Line
Another way that we can represent the equation of a line is in standard form. Standard form is given as
where
Find the equation of the line with
Solution
We begin using the point-slope formula.
From here, we multiply through by
This equation is now written in standard form.
Find the equation of the line in standard form with slope
- Answer
-
Vertical and Horizontal Lines
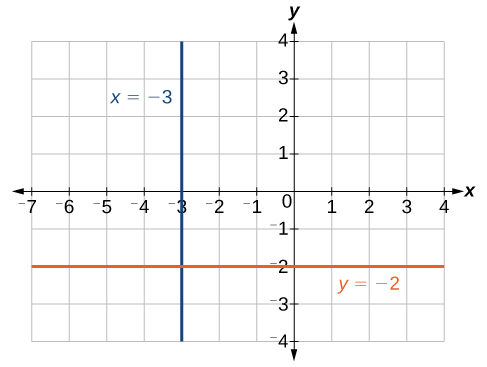
The equations of vertical and horizontal lines do not require any of the preceding formulas, although we can use the formulas to prove that the equations are correct. The equation of a vertical line is given as
where
Suppose that we want to find the equation of a line containing the following points:
Zero in the denominator means that the slope is undefined and, therefore, we cannot use the point-slope formula. However, we can plot the points. Notice that all of the
The equation of a horizontal line is given as
where
Suppose we want to find the equation of a line that contains the following set of points:
Use any point for
The graph is a horizontal line through
Find the equation of the line passing through the given points:
Solution
The
Find the equation of the line passing through
- Answer
-
Horizontal line:
Determining Whether Graphs of Lines are Parallel or Perpendicular
Parallel lines have the same slope and different y-intercepts. Lines that are parallel to each other will never intersect. For example, Figure
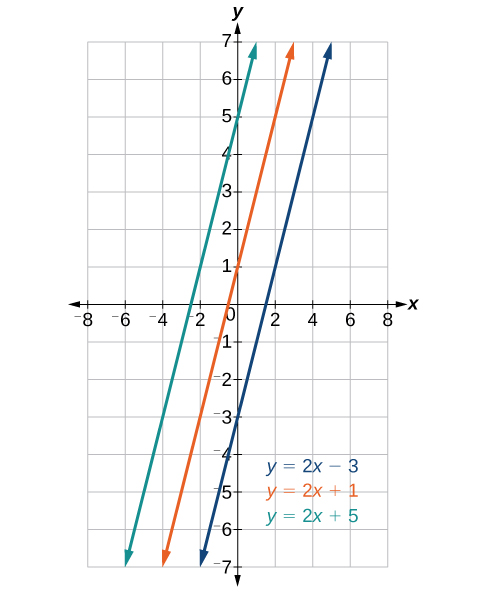
All of the lines shown in the graph are parallel because they have the same slope and different y-intercepts.
Lines that are perpendicular intersect to form a
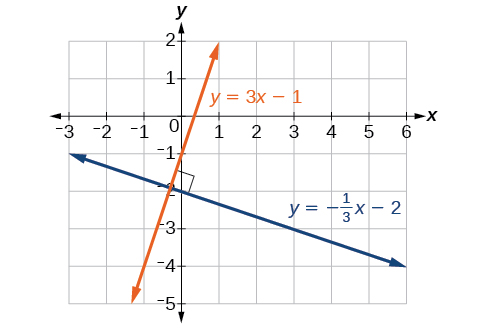
Graph the equations of the given lines, and state whether they are parallel, perpendicular, or neither:
Solution
The first thing we want to do is rewrite the equations so that both equations are in slope-intercept form.
First equation:
Second equation:
See the graph of both lines in Figure
From the graph, we can see that the lines appear perpendicular, but we must compare the slopes.
The slopes are negative reciprocals of each other, confirming that the lines are perpendicular.
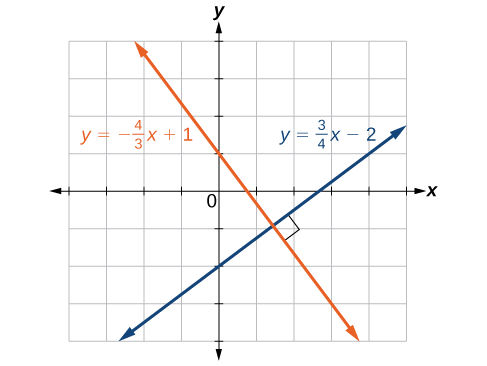
Graph the two lines and determine whether they are parallel, perpendicular, or neither:
- Answer
-
Parallel lines: equations are written in slope-intercept form.
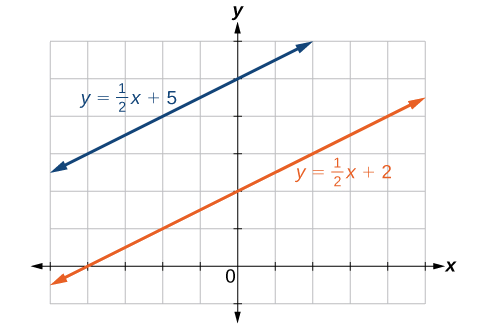
Figure
Writing the Equations of Lines Parallel or Perpendicular to a Given Line
As we have learned, determining whether two lines are parallel or perpendicular is a matter of finding the slopes. To write the equation of a line parallel or perpendicular to another line, we follow the same principles as we do for finding the equation of any line. After finding the slope, use the point-slope formula to write the equation of the new line.
- Find the slope of the given line. The easiest way to do this is to write the equation in slope-intercept form.
- Use the slope and the given point with the point-slope formula.
- Simplify the line to slope-intercept form and compare the equation to the given line.
Write the equation of line parallel to a
Solution
First, we will write the equation in slope-intercept form to find the slope.
The slope is
The equation of the line is
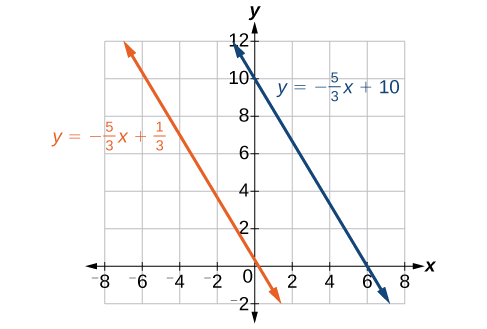
Find the equation of the line parallel to
- Answer
-
Find the equation of the line perpendicular to
Solution
The first step is to write the equation in slope-intercept form.
We see that the slope is
Access these online resources for additional instruction and practice with linear equations.
- Solving rational equations
- Equation of a line given two points
- Finding the equation of a line perpendicular to another line through a given point
- Finding the equation of a line parallel to another line through a given point
Key Concepts
- We can solve linear equations in one variable in the form
- A rational expression is a quotient of two polynomials. We use the LCD to clear the fractions from an equation. See Example and Example.
- All solutions to a rational equation should be verified within the original equation to avoid an undefined term, or zero in the denominator. See Example and Example.
- Given two points, we can find the slope of a line using the slope formula. See Example.
- We can identify the slope and
- We can find the equation of a line given the slope and a point. See Example.
- We can also find the equation of a line given two points. Find the slope and use the point-slope formula. See Example.
- The standard form of a line has no fractions. See Example.
- Horizontal lines have a slope of zero and are defined as
- Vertical lines have an undefined slope (zero in the denominator), and are defined as
- Parallel lines have the same slope and different
- Perpendicular lines have slopes that are negative reciprocals of each other unless one is horizontal and the other is vertical. See Example.
Contributors and Attributions
The OpenStax College name, OpenStax College logo, OpenStax College book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the creative commons license and may not be reproduced without the prior and express written consent of Rice University. For questions regarding this license, please contact partners@openstaxcollege.org. If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Models and Applications. OpenStax CNX. Apr 1, 2015 http://cnx.org/contents/c49b7453-abd...baac08df9ebc@4. If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/c49b7453-abd...baac08df9ebc@4." If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/c49b7453-abd...baac08df9ebc@4."


