3.1E: Functions and Function Notation (Exercises)

Last updated
Save as PDF

Page ID: 56069

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

For the following exercises, determine whether the relation is a function.

1. $\{(a, b),(c, d),(e, d)\}$
2. \{(5,2),(6,1),(6,2),(4,8)\}\)
3. $y^{2}+4=x,$ for $x$ the independent variable and $y$ the dependent variable
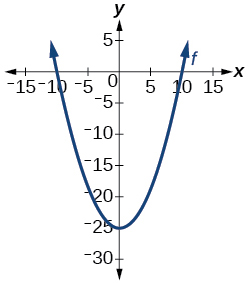
4. Is the graph in Figure 1 a function?

$Graph of a parabola.$

For the following exercises, evaluate the function at the indicated values:

\[\begin{array}{lllll} f(-3) ; & f(2) ; & f(-a) ; & -f(a) ; & f(a+h) .\end{array} \nonumber\]

5. $f(x)=-2 x^{2}+3 x$
6. $f(x)=2|3 x-1|$

For the following exercises, determine whether the functions are one-to-one.

7. $f(x)=-3 x+5$
8. $f(x)=\mid x-3$

For the following exercises, use the vertical line test to determine if the relation whose graph is provided is a function.

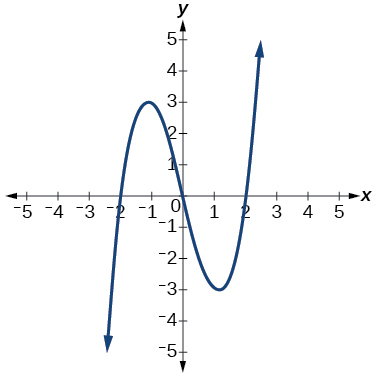
$Graph of a cubic function.$

10.

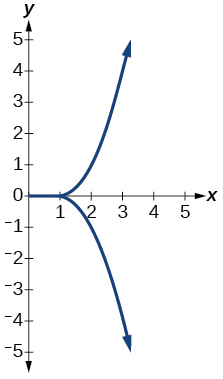
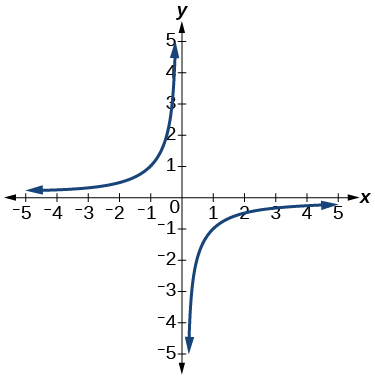
$Graph of a relation.$

11.

$Graph of a relation.$

For the following exercises, graph the functions.

12. $f(x)=\mid x+1$
13. $f(x)=x^{2}-2$

For the following exercises, use Figure 2 to approximate the values.

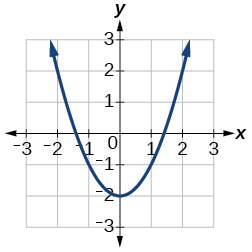
$Graph of a parabola.$

14. $f(2)$
15. $f(-2)$
16. If $f(x)=-2,$ then solve for $x$.
17. If $f(x)=1,$ then solve for $x$.

For the following exercises, use the function $h(t)=-16 t^{2}+80 t$ to find the values in simplest form.

18. $\frac{h(2)-h(1)}{2-1}$
19. $\frac{h(a)-h(1)}{a-1}$