9.5: Solving Trigonometric Equations

Learning Objectives

• Solve linear trigonometric equations in sine and cosine.
• Solve equations involving a single trigonometric function.
• Solve trigonometric equations using a calculator.
• Solve trigonometric equations that are quadratic in form.
• Solve trigonometric equations using fundamental identities.
• Solve trigonometric equations with multiple angles.
• Solve right triangle problems.

Thales of Miletus (circa 625–547 BC) is known as the founder of geometry. The legend is that he calculated the height of the Great Pyramid of Giza in Egypt using the theory of similar triangles, which he developed by measuring the shadow of his staff. Based on proportions, this theory has applications in a number of areas, including fractal geometry, engineering, and architecture. Often, the angle of elevation and the angle of depression are found using similar triangles.

Figure $\PageIndex{1}$: Egyptian pyramids standing near a modern city. (credit: Oisin Mulvihill)

In earlier sections of this chapter, we looked at trigonometric identities. Identities are true for all values in the domain of the variable. In this section, we begin our study of trigonometric equations to study real-world scenarios such as the finding the dimensions of the pyramids.

Solving Linear Trigonometric Equations in Sine and Cosine

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is $2\pi$. In other words, every $2\pi$ units, the y-values repeat. If we need to find all possible solutions, then we must add $2\pi k$,where $k$ is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is $2\pi$:

$$\sin \theta=\sin(\theta \pm 2k\pi)$$

There are similar rules for indicating all possible solutions for the other trigonometric functions. Solving trigonometric equations requires the same techniques as solving algebraic equations. We read the equation from left to right, horizontally, like a sentence. We look for known patterns, factor, find common denominators, and substitute certain expressions with a variable to make solving a more straightforward process. However, with trigonometric equations, we also have the advantage of using the identities we developed in the previous sections.

Example $\PageIndex{1A}$: Solving a Linear Trigonometric Equation Involving the Cosine Function

Find all possible exact solutions for the equation $\cos \theta=\dfrac{1}{2}$.

Solution

From the unit circle, we know that

$$\begin{align*} \cos \theta &=\dfrac{1}{2} \\[4pt] \theta &=\dfrac{\pi}{3},\space \dfrac{5\pi}{3} \end{align*}$$

These are the solutions in the interval $[ 0,2\pi ]$. All possible solutions are given by

$$\theta=\dfrac{\pi}{3} \pm 2k\pi \quad \text{and} \quad \theta=\dfrac{5\pi}{3} \pm 2k\pi \nonumber$$

where $k$ is an integer.

Example $\PageIndex{1B}$: Solving a Linear Equation Involving the Sine Function

Find all possible exact solutions for the equation $\sin t=\dfrac{1}{2}$.

Solution

Solving for all possible values of $t$ means that solutions include angles beyond the period of $2\pi$. From the section on Sum and Difference Identities, we can see that the solutions are $t=\dfrac{\pi}{6}$ and $t=\dfrac{5\pi}{6}$. But the problem is asking for all possible values that solve the equation. Therefore, the answer is

$$t=\dfrac{\pi}{6}\pm 2\pi k \quad \text{and} \quad t=\dfrac{5\pi}{6}\pm 2\pi k \nonumber$$

where $k$ is an integer.

Howto: Given a trigonometric equation, solve using algebra

1. Look for a pattern that suggests an algebraic property, such as the difference of squares or a factoring opportunity.
2. Substitute the trigonometric expression with a single variable, such as $x$ or $u$.
3. Solve the equation the same way an algebraic equation would be solved.
4. Substitute the trigonometric expression back in for the variable in the resulting expressions.
5. Solve for the angle.

Example $\PageIndex{2}$: Solve the Linear Trigonometric Equation

Solve the equation exactly: $2 \cos \theta−3=−5$, $0≤\theta<2\pi$.

Solution

Use algebraic techniques to solve the equation.

$$\begin{align*} 2 \cos \theta-3&= -5\\ 2 \cos \theta&= -2\\ \cos \theta&= -1\\ \theta&= \pi \end{align*}$$

Exercise $\PageIndex{2}$

Solve exactly the following linear equation on the interval $[0,2\pi)$: $2 \sin x+1=0$.

Answer

$x=\dfrac{7\pi}{6},\space \dfrac{11\pi}{6}$

Solving Equations Involving a Single Trigonometric Function

When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and the unit circle (see [link]). We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems involving the reciprocals of the primary trigonometric functions need to be viewed from an algebraic perspective. In other words, we will write the reciprocal function, and solve for the angles using the function. Also, an equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is $\pi$,not $2\pi$. Further, the domain of tangent is all real numbers with the exception of odd integer multiples of $\dfrac{\pi}{2}$,unless, of course, a problem places its own restrictions on the domain.

Solving a Problem Involving a Single Trigonometric Function

Solve the problem exactly: $2 {\sin}^2 \theta−1=0$, $0≤\theta<2\pi$.

Solution

As this problem is not easily factored, we will solve using the square root property. First, we use algebra to isolate $\sin \theta$. Then we will find the angles.

$$\begin{align*} 2 {\sin}^2 \theta-1&= 0\\ 2 {\sin}^2 \theta&= 1\\ {\sin}^2 \theta&= \dfrac{1}{2}\\ \sqrt{ {\sin}^2 \theta }&= \pm \sqrt{ \dfrac{1}{2} }\\ \sin \theta&= \pm \dfrac{1}{\sqrt{2}}\\ &= \pm \dfrac{\sqrt{2}}{2}\\ \theta&= \dfrac{\pi}{4}, \space \dfrac{3\pi}{4},\space \dfrac{5\pi}{4}, \space \dfrac{7\pi}{4} \end{align*}$$

Example $\PageIndex{3B}$: Solving a Trigonometric Equation Involving Cosecant

Solve the following equation exactly: $\csc \theta=−2$, $0≤\theta<4\pi$.

Solution

We want all values of $\theta$ for which $\csc \theta=−2$ over the interval $0≤\theta<4\pi$.

$$\begin{align*} \csc \theta&= -2\\ \dfrac{1}{\sin \theta}&= -2\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\space \dfrac{11\pi}{6},\space \dfrac{19\pi}{6}, \space \dfrac{23\pi}{6} \end{align*}$$

Analysis

As $\sin \theta=−\dfrac{1}{2}$, notice that all four solutions are in the third and fourth quadrants.

Example $\PageIndex{3C}$: Solving an Equation Involving Tangent

Solve the equation exactly: $\tan\left(\theta−\dfrac{\pi}{2}\right)=1$, $0≤\theta<2\pi$.

Solution

Recall that the tangent function has a period of $\pi$. On the interval $[ 0,\pi )$,and at the angle of $\dfrac{\pi}{4}$,the tangent has a value of $1$. However, the angle we want is $\left(\theta−\dfrac{\pi}{2}\right)$. Thus, if $\tan\left(\dfrac{\pi}{4}\right)=1$,then

$$\begin{align*} \theta-\dfrac{\pi}{2}&= \dfrac{\pi}{4}\\ \theta&= \dfrac{3\pi}{4} \pm k\pi \end{align*}$$

Over the interval $[ 0,2\pi )$,we have two solutions:

$\theta=\dfrac{3\pi}{4}$ and $\theta=\dfrac{3\pi}{4}+\pi=\dfrac{7\pi}{4}$

Exercise $\PageIndex{3}$

Find all solutions for $\tan x=\sqrt{3}$.

Answer

$\dfrac{\pi}{3}\pm \pi k$

Example $\PageIndex{4}$: Identify all Solutions to the Equation Involving Tangent

Identify all exact solutions to the equation $2(\tan x+3)=5+\tan x$, $0≤x<2\pi$.

Solution

We can solve this equation using only algebra. Isolate the expression $\tan x$ on the left side of the equals sign.

$$\begin{align*} 2(\tan x)+2(3)&= 5+\tan x\\ 2\tan x+6&= 5+\tan x\\ 2\tan x-\tan x&= 5-6\\ \tan x&= -1 \end{align*}$$

There are two angles on the unit circle that have a tangent value of $−1$: $\theta=\dfrac{3\pi}{4}$ and $\theta=\dfrac{7\pi}{4}$.

Solve Trigonometric Equations Using a Calculator

Not all functions can be solved exactly using only the unit circle. When we must solve an equation involving an angle other than one of the special angles, we will need to use a calculator. Make sure it is set to the proper mode, either degrees or radians, depending on the criteria of the given problem.

Example $\PageIndex{5A}$: Using a Calculator to Solve a Trigonometric Equation Involving Sine

Use a calculator to solve the equation $\sin \theta=0.8$,where $\theta$ is in radians.

Solution

Make sure mode is set to radians. To find $\theta$, use the inverse sine function. On most calculators, you will need to push the 2^ND button and then the SIN button to bring up the ${\sin}^{−1}$ function. What is shown on the screen is ${\sin}^{−1}$.The calculator is ready for the input within the parentheses. For this problem, we enter ${\sin}^{−1}(0.8)$, and press ENTER. Thus, to four decimals places,

${\sin}^{−1}(0.8)≈0.9273$

The solution is

$\theta≈0.9273\pm 2\pi k$

The angle measurement in degrees is

$$\begin{align*} \theta&\approx 53.1^{\circ}\\ \theta&\approx 180^{\circ}-53.1^{\circ}\\ &\approx 126.9^{\circ} \end{align*}$$

Analysis

Note that a calculator will only return an angle in quadrants I or IV for the sine function, since that is the range of the inverse sine. The other angle is obtained by using $\pi−\theta$.

Example $\PageIndex{5B}$: Using a Calculator to Solve a Trigonometric Equation Involving Secant

Use a calculator to solve the equation $\sec θ=−4,$ giving your answer in radians.

Solution

We can begin with some algebra.

$$\begin{align*} \sec \theta&= -4\\ \dfrac{1}{\cos \theta}&= -4\\ \cos \theta&= -\dfrac{1}{4} \end{align*}$$

Check that the MODE is in radians. Now use the inverse cosine function

$$\begin{align*}{\cos}^{-1}\left(-\dfrac{1}{4}\right)&\approx 1.8235\\ \theta&\approx 1.8235+2\pi k \end{align*}$$

Since $\dfrac{\pi}{2}≈1.57$ and $\pi≈3.14$,$1.8235$ is between these two numbers, thus $\theta≈1.8235$ is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the cosine function, since that is the range of the inverse cosine. See Figure $\PageIndex{2}$.

Figure $\PageIndex{2}$

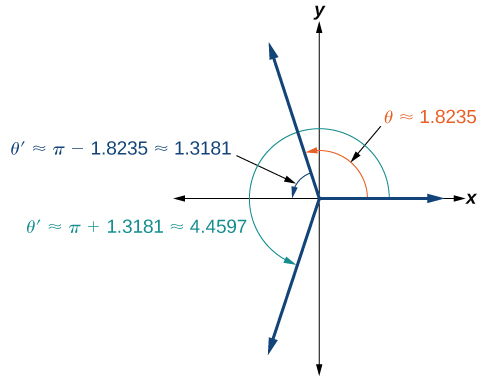
So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is $\theta '≈\pi−1.8235≈1.3181$. The other solution in quadrant III is $\theta '≈\pi+1.3181≈4.4597$.

The solutions are $\theta≈1.8235\pm 2\pi k$ and $\theta≈4.4597\pm 2\pi k$.

Exercise $\PageIndex{5}$

Solve $\cos \theta=−0.2$.

Answer

$\theta≈1.7722\pm 2\pi k$ and $\theta≈4.5110\pm 2\pi k$

Solving Trigonometric Equations in Quadratic Form

Solving a quadratic equation may be more complicated, but once again, we can use algebra as we would for any quadratic equation. Look at the pattern of the equation. Is there more than one trigonometric function in the equation, or is there only one? Which trigonometric function is squared? If there is only one function represented and one of the terms is squared, think about the standard form of a quadratic. Replace the trigonometric function with a variable such as $x$ or $u$. If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.

Example $\PageIndex{6A}$: Solving a Trigonometric Equation in Quadratic Form

Solve the equation exactly: ${\cos}^2 \theta+3 \cos \theta−1=0$, $0≤\theta<2\pi$.

Solution

We begin by using substitution and replacing $\cos \theta$ with $x$. It is not necessary to use substitution, but it may make the problem easier to solve visually. Let $\cos \theta=x$. We have

$x^2+3x−1=0$

The equation cannot be factored, so we will use the quadratic formula: $x=\dfrac{−b\pm \sqrt{b^2−4ac}}{2a}$.

$$\begin{align*} x&= \dfrac{ -3\pm \sqrt{ {(-3)}^2-4 (1) (-1) } }{2}\\ &= \dfrac{-3\pm \sqrt{13}}{2}\end{align*}$$

Replace $x$ with $\cos \theta$ and solve.

$$\begin{align*} \cos \theta&= \dfrac{-3\pm \sqrt{13}}{2}\\ \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \end{align*}$$

Note that only the + sign is used. This is because we get an error when we solve $\theta={\cos}^{−1}\left(\dfrac{−3−\sqrt{13}}{2}\right)$ on a calculator, since the domain of the inverse cosine function is $[ −1,1 ]$. However, there is a second solution:

$$\begin{align*} \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 1.26 \end{align*}$$

This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is

$$\begin{align*} \theta&= 2\pi-{\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 5.02 \end{align*}$$

Example $\PageIndex{6B}$: Solving a Trigonometric Equation in Quadratic Form by Factoring

Solve the equation exactly: $2 {\sin}^2 \theta−5 \sin \theta+3=0$, $0≤\theta≤2\pi$.

Solution

Using grouping, this quadratic can be factored. Either make the real substitution, $\sin \theta=u$,or imagine it, as we factor:

$$\begin{align*} 2 {\sin}^2 \theta-5 \sin \theta+3&= 0\\ (2 \sin \theta-3)(\sin \theta-1)&= 0 \qquad \text {Now set each factor equal to zero.}\\ 2 \sin \theta-3&= 0\\ 2 \sin \theta&= 3\\ \sin \theta&= \dfrac{3}{2}\\ \sin \theta-1&= 0\\ \sin \theta&= 1 \end{align*}$$

Next solve for $\theta$: $\sin \theta≠\dfrac{3}{2}$, as the range of the sine function is $[ −1,1 ]$. However, $\sin \theta=1$, giving the solution $\theta=\dfrac{\pi}{2}$.

Analysis

Make sure to check all solutions on the given domain as some factors have no solution.

Exercise $\PageIndex{6}$

Solve ${\sin}^2 \theta=2 \cos \theta+2$, $0≤\theta≤2\pi$. [Hint: Make a substitution to express the equation only in terms of cosine.]

Answer

$\cos \theta=−1$, $\theta=\pi$

Example $\PageIndex{7A}$: Solving a Trigonometric Equation Using Algebra

Solve exactly: $2 {\sin}^2 \theta+\sin \theta=0;\space 0≤\theta<2\pi$

Solution

This problem should appear familiar as it is similar to a quadratic. Let $\sin \theta=x$. The equation becomes $2x^2+x=0$. We begin by factoring:

$$\begin{align*} 2x^2+x&= 0\\ x(2x+1)&= 0\qquad \text {Set each factor equal to zero.}\\ x&= 0\\ 2x+1&= 0\\ x&= -\dfrac{1}{2} \end{align*}$$
Then, substitute back into the equation the original expression $\sin \theta$ for $x$. Thus,
$$\begin{align*} \sin \theta&= 0\\ \theta&= 0,\pi\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\dfrac{11\pi}{6} \end{align*}$$

The solutions within the domain $0≤\theta<2\pi$ are $\theta=0,\pi,\dfrac{7\pi}{6},\dfrac{11\pi}{6}$.

If we prefer not to substitute, we can solve the equation by following the same pattern of factoring and setting each factor equal to zero.

$$\begin{align*} {\sin}^2 \theta+\sin \theta&= 0\\ \sin \theta(2\sin \theta+1)&= 0\\ \sin \theta&= 0\\ \theta&= 0,\pi\\ 2 \sin \theta+1&= 0\\ 2\sin \theta&= -1\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\dfrac{11\pi}{6} \end{align*}$$

Analysis

We can see the solutions on the graph in Figure $\PageIndex{3}$. On the interval $0≤\theta<2\pi$,the graph crosses the $x$-axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.

Figure $\PageIndex{3}$

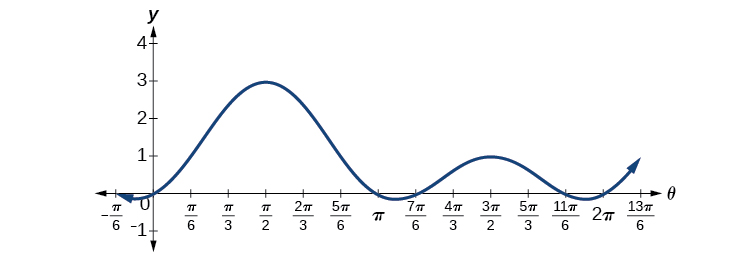
We can verify the solutions on the unit circle in via the result in the section on Sum and Difference Identities as well.

Example $\PageIndex{7B}$: Solving a Trigonometric Equation Quadratic in Form

Solve the equation quadratic in form exactly: $2 {\sin}^2 \theta−3 \sin \theta+1=0$, $0≤\theta<2\pi$.

Solution

We can factor using grouping. Solution values of $\theta$ can be found on the unit circle.

$$\begin{align*} (2 \sin \theta-1)(\sin \theta-1)&= 0\\ 2 \sin \theta-1&= 0\\ \sin \theta&= \dfrac{1}{2}\\ \theta&= \dfrac{\pi}{6}, \dfrac{5\pi}{6}\\ \sin \theta&= 1\\ \theta&= \dfrac{\pi}{2} \end{align*}$$

Exercise $\PageIndex{7}$

Solve the quadratic equation $2{\cos}^2 \theta+\cos \theta=0$.

Answer

$\dfrac{\pi}{2}, \space \dfrac{2\pi}{3}, \space \dfrac{4\pi}{3}, \space \dfrac{3\pi}{2}$

Solving Trigonometric Equations Using Fundamental Identities

While algebra can be used to solve a number of trigonometric equations, we can also use the fundamental identities because they make solving equations simpler. Remember that the techniques we use for solving are not the same as those for verifying identities. The basic rules of algebra apply here, as opposed to rewriting one side of the identity to match the other side. In the next example, we use two identities to simplify the equation.

Example $\PageIndex{8A}$: Use Identities to Solve an Equation

Use identities to solve exactly the trigonometric equation over the interval $0≤x<2\pi$.

$\cos x \cos(2x)+\sin x \sin(2x)=\dfrac{\sqrt{3}}{2}$

Solution

Notice that the left side of the equation is the difference formula for cosine.

$$\begin{align*} \cos x \cos(2x)+\sin x \sin(2x)&= \dfrac{\sqrt{3}}{2}\\ \cos(x-2x)&= \dfrac{\sqrt{3}}{2}\qquad \text{Difference formula for cosine}\\ \cos(-x)&= \dfrac{\sqrt{3}}{2}\qquad \text{Use the negative angle identity.}\\ \cos x&= \dfrac{\sqrt{3}}{2} \end{align*}$$

From the unit circle in the section on Sum and Difference Identities, we see that $\cos x=\dfrac{\sqrt{3}}{2}$ when $x=\dfrac{\pi}{6},\space \dfrac{11\pi}{6}$.

Example $\PageIndex{8B}$: Solving the Equation Using a Double-Angle Formula

Solve the equation exactly using a double-angle formula: $\cos(2\theta)=\cos \theta$.

Solution

We have three choices of expressions to substitute for the double-angle of cosine. As it is simpler to solve for one trigonometric function at a time, we will choose the double-angle identity involving only cosine:

$$\begin{align*} \cos(2\theta)&= \cos \theta\\ 2{\cos}^2 \theta-1&= \cos \theta\\ 2 {\cos}^2 \theta-\cos \theta-1&= 0\\ (2 \cos \theta+1)(\cos \theta-1)&= 0\\ 2 \cos \theta+1&= 0\\ \cos \theta&= -\dfrac{1}{2}\\ \cos \theta-1&= 0\\ \cos \theta&= 1 \end{align*}$$

So, if $\cos \theta=−\dfrac{1}{2}$,then $\theta=\dfrac{2\pi}{3}\pm 2\pi k$ and $\theta=\dfrac{4\pi}{3}\pm 2\pi k$; if $\cos \theta=1$,then $\theta=0\pm 2\pi k$.

Example $\PageIndex{8C}$: Solving an Equation Using an Identity

Solve the equation exactly using an identity: $3 \cos \theta+3=2 {\sin}^2 \theta$, $0≤\theta<2\pi$.

Solution

If we rewrite the right side, we can write the equation in terms of cosine:

$$\begin{align*} 3 \cos \theta+3&= 2 {\sin}^2 \theta\\ 3 \cos \theta+3&= 2(1-{\cos}^2 \theta)\\ 3 \cos \theta+3&= 2-2{\cos}^2 \theta\\ 2 {\cos}^2 \theta+3 \cos \theta+1&= 0\\ (2 \cos \theta+1)(\cos \theta+1)&= 0\\ 2 \cos \theta+1&= 0\\ \cos \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{2\pi}{3},\space \dfrac{4\pi}{3}\\ \cos \theta+1&= 0\\ \cos \theta&= -1\\ \theta&= \pi\\ \end{align*}$$

Our solutions are $\theta=\dfrac{2\pi}{3},\space \dfrac{4\pi}{3},\space \pi$.

Solving Trigonometric Equations with Multiple Angles

Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle, such as $\sin(2x)$ or $\cos(3x)$. When confronted with these equations, recall that $y=\sin(2x)$ is a horizontal compression by a factor of 2 of the function $y=\sin x$. On an interval of $2\pi$,we can graph two periods of $y=\sin(2x)$,as opposed to one cycle of $y=\sin x$. This compression of the graph leads us to believe there may be twice as many x-intercepts or solutions to $\sin(2x)=0$ compared to $\sin x=0$. This information will help us solve the equation.

Example $\PageIndex{9}$: Solving a Multiple Angle Trigonometric Equation

Solve exactly: $\cos(2x)=\dfrac{1}{2}$ on $[ 0,2\pi )$.

Solution

We can see that this equation is the standard equation with a multiple of an angle. If $\cos(\alpha)=\dfrac{1}{2}$,we know $\alpha$ is in quadrants I and IV. While $\theta={\cos}^{−1} \dfrac{1}{2}$ will only yield solutions in quadrants I and II, we recognize that the solutions to the equation $\cos \theta=\dfrac{1}{2}$ will be in quadrants I and IV.

Therefore, the possible angles are $\theta=\dfrac{\pi}{3}$ and $\theta=\dfrac{5\pi}{3}$. So, $2x=\dfrac{\pi}{3}$ or $2x=\dfrac{5\pi}{3}$, which means that $x=\dfrac{\pi}{6}$ or $x=\dfrac{5\pi}{6}$. Does this make sense? Yes, because $\cos\left(2\left(\dfrac{\pi}{6}\right)\right)=\cos\left(\dfrac{\pi}{3}\right)=\dfrac{1}{2}$.

Are there any other possible answers? Let us return to our first step.

In quadrant I, $2x=\dfrac{\pi}{3}$, so $x=\dfrac{\pi}{6}$ as noted. Let us revolve around the circle again:

$$\begin{align*} 2x&= \dfrac{\pi}{3}+2\pi\\ &= \dfrac{\pi}{3}+\dfrac{6\pi}{3}\\ &= \dfrac{7\pi}{3}\\ x&= \dfrac{7\pi}{6}\\ \text {One more rotation yields}\\ 2x&= \dfrac{\pi}{3}+4\pi\\ &= \dfrac{\pi}{3}+\dfrac{12\pi}{3}\\ &= \dfrac{13\pi}{3}\\ \end{align*}$$

$x=\dfrac{13\pi}{6}>2\pi$, so this value for $x$ is larger than $2\pi$, so it is not a solution on $[ 0,2\pi )$.

In quadrant IV, $2x=\dfrac{5\pi}{3}$, so $x=\dfrac{5\pi}{6}$ as noted. Let us revolve around the circle again:

$$\begin{align*} 2x&= \dfrac{5\pi}{3}+2\pi\\ &= \dfrac{5\pi}{3}+\dfrac{6\pi}{3}\\ &= \dfrac{11\pi}{3} \end{align*}$$

so $x=\dfrac{11\pi}{6}$.

One more rotation yields

$$\begin{align*} 2x&= \dfrac{5\pi}{3}+4\pi\\ &= \dfrac{5\pi}{3}+\dfrac{12\pi}{3}\\ &= \dfrac{17\pi}{3} \end{align*}$$

$x=\dfrac{17\pi}{6}>2\pi$,so this value for $x$ is larger than $2\pi$,so it is not a solution on $[ 0,2\pi )$.

Our solutions are $x=\dfrac{\pi}{6}, \space \dfrac{5\pi}{6}, \space \dfrac{7\pi}{6}$, and $\dfrac{11\pi}{6}$. Note that whenever we solve a problem in the form of $sin(nx)=c$, we must go around the unit circle $n$ times.

Solving Right Triangle Problems

We can now use all of the methods we have learned to solve problems that involve applying the properties of right triangles and the Pythagorean Theorem. We begin with the familiar Pythagorean Theorem,

$$a^2+b^2=c^2 \label{Pythagorean}$$

and model an equation to fit a situation.

Example $\PageIndex{10A}$: Using the Pythagorean Theorem to Model an Equation

One of the cables that anchors the center of the London Eye Ferris wheel to the ground must be replaced. The center of the Ferris wheel is $69.5$ meters above the ground, and the second anchor on the ground is $23$ meters from the base of the Ferris wheel. Approximately how long is the cable, and what is the angle of elevation (from ground up to the center of the Ferris wheel)? See Figure $\PageIndex{4}$.

Figure $\PageIndex{4}$

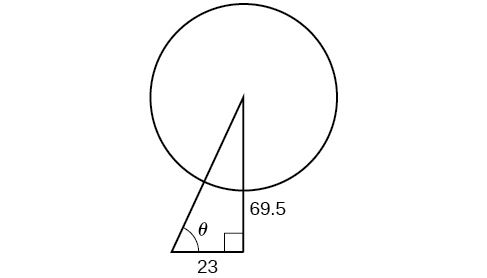
Solution

Use the Pythagorean Theorem (Equation $\ref{Pythagorean}$) and the properties of right triangles to model an equation that fits the problem. Using the information given, we can draw a right triangle. We can find the length of the cable with the Pythagorean Theorem.

$$\begin{align*} a^2+b^2&= c^2\\ {(23)}^2+{(69.5)}^2&\approx 5359\\ \sqrt{5359}&\approx 73.2\space m \end{align*}$$

The angle of elevation is $\theta$,formed by the second anchor on the ground and the cable reaching to the center of the wheel. We can use the tangent function to find its measure. Round to two decimal places.

$$\begin{align*} \tan \theta&= 69.523\\ {\tan}^{-1}(69.523)&\approx 1.2522\\ &\approx 71.69^{\circ} \end{align*}$$

The angle of elevation is approximately $71.7°$, and the length of the cable is $73.2$ meters.

Example $\PageIndex{10B}$: Using the Pythagorean Theorem to Model an Abstract Problem

OSHA safety regulations require that the base of a ladder be placed $1$ foot from the wall for every $4$ feet of ladder length. Find the angle that a ladder of any length forms with the ground and the height at which the ladder touches the wall.

Solution

For any length of ladder, the base needs to be a distance from the wall equal to one fourth of the ladder’s length. Equivalently, if the base of the ladder is “a” feet from the wall, the length of the ladder will be $4a$ feet. See Figure $\PageIndex{5}$.

Figure $\PageIndex{5}$

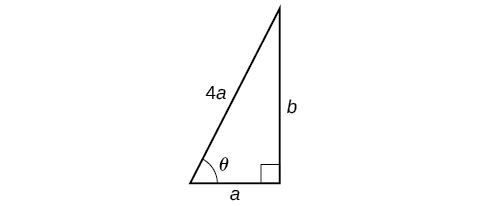
The side adjacent to $\theta$ is $a$ and the hypotenuse is $4a$. Thus,

$$\begin{align*} \cos \theta&= \dfrac{a}{4a}\\ &= \dfrac{1}{4}\\ {\cos}^{-1}\left (\dfrac{1}{4}\right )&\approx 75.5^{\circ} \end{align*}$$

The elevation of the ladder forms an angle of $75.5°$ with the ground. The height at which the ladder touches the wall can be found using the Pythagorean Theorem:

$$\begin{align*} a^2+b^2&= {(4a)}^2\\ b^2&= {(4a)}^2-a^2\\ b^2&= 16a^2-a^2\\ b^2&= 15a^2\\ b&= a\sqrt{15} \end{align*}$$

Thus, the ladder touches the wall at $a\sqrt{15}$ feet from the ground.

Media

Access these online resources for additional instruction and practice with solving trigonometric equations.

• Solving Trigonometric Equations I
• Solving Trigonometric Equations II
• Solving Trigonometric Equations III
• Solving Trigonometric Equations IV
• Solving Trigonometric Equations V
• Solving Trigonometric Equations VI

Key Concepts

• When solving linear trigonometric equations, we can use algebraic techniques just as we do solving algebraic equations. Look for patterns, like the difference of squares, quadratic form, or an expression that lends itself well to substitution. See Example $\PageIndex{1}$, Example $\PageIndex{2}$, and Example $\PageIndex{3}$.
• Equations involving a single trigonometric function can be solved or verified using the unit circle. See Example $\PageIndex{4}$, Example $\PageIndex{5}$, and Example $\PageIndex{6}$, and Example $\PageIndex{7}$.
• We can also solve trigonometric equations using a graphing calculator. See Example $\PageIndex{8}$ and Example $\PageIndex{9}$.
• Many equations appear quadratic in form. We can use substitution to make the equation appear simpler, and then use the same techniques we use solving an algebraic quadratic: factoring, the quadratic formula, etc. See Example $\PageIndex{10}$, Example $\PageIndex{11}$, Example $\PageIndex{12}$, and Example $\PageIndex{13}$.
• We can also use the identities to solve trigonometric equation. See Example $\PageIndex{14}$, Example $\PageIndex{15}$, and Example $\PageIndex{16}$.
• We can use substitution to solve a multiple-angle trigonometric equation, which is a compression of a standard trigonometric function. We will need to take the compression into account and verify that we have found all solutions on the given interval. See Example $\PageIndex{17}$.
• Real-world scenarios can be modeled and solved using the Pythagorean Theorem and trigonometric functions. See Example $\PageIndex{18}$.