1.2: Adding and Subtracting Integers
- Page ID
- 18327
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Add and subtract signed integers.
- Translate English sentences involving addition and subtraction into mathematical statements.
- Calculate the distance between two numbers on a number line.
Addition and Subtraction \((+, -)\)
Visualize adding \(3 + 2\) on the number line by moving from zero three units to the right then another two units to the right, as illustrated below:

The illustration shows that \(3 + 2 = 5\). Similarly, visualize adding two negative numbers \((−3) + (−2)\) by first moving from the origin three units to the left and then moving another two units to the left.

In this example, the illustration shows \((−3) + (−2) = −5\), which leads to the following two properties of real numbers.
\[\begin{align*} & \color{Cerulean}{positive\ number\;} \color{Black}{+\;} \color{Cerulean}{positive\ number\;} \color{Black}{=\;} \color{Cerulean}{positive\ number} \\ & \color{Cerulean}{negative\ number\;} \color{Black}{+\;} \color{Cerulean}{negative\ number\;} \color{Black}{=\;} \color{Cerulean}{negative\ number} \end{align*}\]
Next, we will explore addition of numbers with unlike signs. To add \(3 + (−7)\), first move from the origin three units to the right, then move seven units to the left as shown:

In this case, we can see that adding a negative number is equivalent to subtraction:
\(3+(-7)=3-7=-4\)
It is tempting to say that a positive number plus a negative number is negative, but that is not always true: \(7+(−3)=7−3=4\). The result of adding numbers with unlike signs may be positive or negative. The sign of the result is the same as the sign of the number with the greatest distance from the origin. For example, the following results depend on the sign of the number \(12\) because it is farther from zero than \(5\):
\[\begin{align*} &12+(-5)=7 \\ &-12+5=-7 \end{align*} \]
Example \(\PageIndex{1}\)
Simplify: \(14+(−25)\).
Solution
Here \(−25\) is the greater distance from the origin. Therefore, the result is negative.
\[\begin{align*} 14+(-25) &= 14-25 \\ &= -11 \end{align*}\]
Answer
\(-11\)
Properties of Addition
Given any real numbers \(a\), \(b\), and \(c\), we have the following properties of addition:
- Additive Identity Property: \[a+0=0+a=a\]
- Additive Inverse Property:\[a+(−a)=(−a)+a=0\]
- Associative Property:\[(a+b)+c=a+(b+c)\]
- Commutative Property:\[a+b=b+a\]
Below are some examples of these properties in action.
Example \(\PageIndex{2}\)
Simplify:
a. \(5+0\)
b. \(10+(−10)\)
Solution
a. Adding zero to any real number results in the same real number.
\[5+0=5 \nonumber\]
b. Adding opposites results in zero.
Answer
a. \(5\); b. \(0\)
Example \(\PageIndex{3}\)
Simplify:
a. \((3+7)+4\)
b. \(3+(7+4)\)
Solution
Parentheses group the operations that are to be performed first.
a. \[\begin{align*} (\color{Cerulean}{3+7} \color{Black}{)}+4 &= \color{Cerulean}{10}\ \color{Black}{+\ 4} \\ &= 14 \end{align*} \]
b. \[\begin{align*} 3+(\color{Cerulean}{7+4} \color{Black}{)} &= 3+ \color{Cerulean}{10} \\ &= 14 \end{align*} \]
These two examples both result in \(14\): changing the grouping of the numbers does not change the result.
\((\color{Cerulean}{3+7} \color{Black}{)} +4=3+(\color{Cerulean}{7+4} \color{Black}{)}=14\)
Answer
a. \(14\); b. \(14\)
At this point, we highlight the fact that addition is commutative: the order in which we add does not matter and yields the same result.
\[\begin{align*} 2+9 &= 9+2 \\ 11 &= 11 \end{align*} \]
On the other hand, subtraction is not commutative.
\[\begin{align*} 2-9 &\neq 9-2 \\ -7 &\neq 7 \end{align*} \]
We will use these properties, along with the double-negative property for real numbers, to perform more involved sequential operations. To simplify things, we will make it a general rule to first replace all sequential operations with either addition or subtraction and then perform each operation in order from left to right.
Example \(\PageIndex{4}\)
Simplify: \(4−(−10)+(−5)\).
Solution
Replace the sequential operations and then perform them from left to right.
\[\begin{align*} 4-(-10)+(-5) &= 4+10-5 && \color{Cerulean}{Replace\ -(-)\ with\ addition\ (+).} \\ & && \color{Cerulean}{Replace\ +(-)\ with\ addition\ (-).} \\ &= 14-5 \\ &=9 \end{align*} \]
Answer
\(9\)
Example \(\PageIndex{5}\)
Simplify: \(−3+(−8)−(−7)\).
Solution
\[\begin{align*} -3+(-8)-(-7) &= -3-8+7 && \color{Cerulean}{Replace\ +(-)\ with\ (-).} \\ & && \color{Cerulean}{Replace\ -(-)\ with\ (+).} \\ &= -11+7 \\ &=-4 \end{align*} \]
Answer
\(-4\)
Example \(\PageIndex{6}\)
Try this!
Simplify: \(12−(−9)+(−6)\).
Solution
(click to see video)
Often we find the need to translate English sentences involving addition and subtraction to mathematical statements. Listed below are some key words that translate to the given operation.
| Key Words | Operation |
| Sum, increased by, more than, plus, added to, total | \(+\) |
| Difference, decreased by, subtracted from, less, minus | \(-\) |
Example \(\PageIndex{7}\)
What is the difference of \(7\) and \(−3\)?
Solution
The key word “difference” implies that we should subtract the numbers.
\[\begin{align*} 7-(-3) &= 7+3 \\ &=10 \end{align*} \]
Answer
The difference of \(7\) and \(−3\) is \(10\).
Example \(\PageIndex{8}\)
What is the sum of the first five positive integers?
Solution
The initial key word to focus on is “sum”; this means that we will be adding the five numbers. The first five positive integers are \(\{1, 2, 3, 4, 5\}\). Recall that \(0\) is neither positive nor negative.
\(1+2+3+4+5=15\)
Answer
The sum of the first five positive integers is \(15\).
Example \(\PageIndex{9}\)
What is \(10\) subtracted from the sum of \(8\) and \(6\)?
Solution
We know that subtraction is not commutative; therefore, we must take care to subtract in the correct order. First, add \(8\) and \(6\) and then subtract \(10\) as follows:
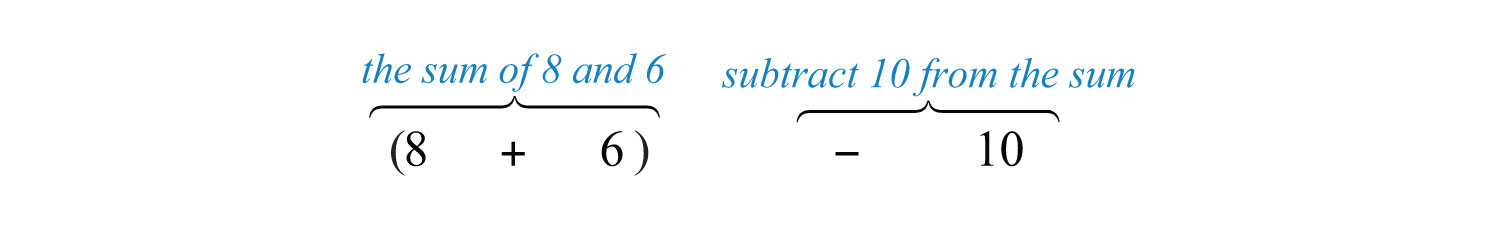
It is important to notice that the phrase “\(10\) subtracted from” does not translate to a mathematical statement in the order it appears. In other words, \(10−(8+6)\) would be an incorrect translation and leads to an incorrect answer. After translating the sentence, perform the operations.
\[\begin{align*} (8+6)-10 &= 14-10 \\ &= 4 \end{align*} \]
Answer
Ten subtracted from the sum of \(8\) and \(6\) is \(4\).
Distance on a Number Line
One application of the absolute value is to find the distance between any two points on a number line. For real numbers \(a\) and \(b\), the distance formula for a number line is given as,
\(d=|b-a|\)
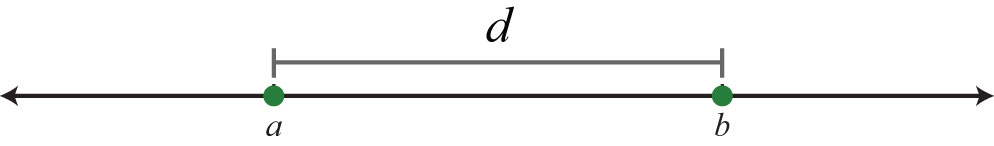
Example \(\PageIndex{10}\)
Determine the distance between \(2\) and \(7\) on a number line.
Solution
On the graph we see that the distance between the two given integers is \(5\) units.

Using the distance formula we obtain the same result.
\[\begin{align*} d &= |7-2| \\ &=|5| \\ &=5 \end{align*} \]
Answer
\(5\) units
Example \(\PageIndex{11}\)
Determine the distance between \(−4\) and \(7\) on a number line.
Solution
Use the distance formula for a number line \(d=|b−a|\), where \(a=−4\) and \(b=7\).
\[\begin{align*} d &= |7-(-4)| \\ &= |7+4| \\ &= |11| \\ &= 11 \end{align*} \]
Answer
\(11\) units
It turns out that it does not matter which points are used for \(a\) and\(b\); the absolute value always ensures a positive result.
| Using \(a = −4\) and \(b = 7\) | Using \(a = 7\) and \(b = −4\) |
| \(d=|7−(−4)|=|7+4|=|11|=11\) | \(d=|−4−7|=|−11|=11\) |
Exercise \(\PageIndex{1}\)
Determine the distance between \(−12\) and \(−9\) on the number line.
- Answer
-
3
Video Solution
(click to see video)
Key Takeaways
- A positive number added to a positive number is positive. A negative number added to a negative number is negative.
- The sign of a positive number added to a negative number is the same as the sign of the number with the greatest distance from the origin.
- Addition is commutative and subtraction is not.
- When simplifying, it is a best practice to first replace sequential operations and then work the operations of addition and subtraction from left to right.
- The distance between any two numbers on a number line is the absolute value of their difference. In other words, given any real numbers a and b, use the formula \(d=|b−a|\) to calculate the distance d between them.
Exercise \(\PageIndex{2}\)
Add and subtract.
- \(24+(−18)\)
- \(9+(−11)\)
- \(−31+5\)
- \(−12+15\)
- \(−30+(−8)\)
- \(−50+(−25)\)
- \(−7+(−7)\)
- \(−13−(−13)\)
- \(8−12+5\)
- \(−3−7+4\)
- \(−1−2−3−4\)
- \(6−(−5)+(−10)−14\)
- \(−5+(−3)−(−7)\)
- \(2−7+(−9)\)
- \(−30+20−8−(−18)\)
- \(10−(−12)+(−8)−20\)
- \(5−(−2)+(−6)\)
- \(−3+(−17)−(−13)\)
- \(−10+(−12)−(−20)\)
- \(−13+(−5)−(−25)\)
- \(20−(−4)−(−5)\)
- \(17+(−12)−(−2)\)
- Answer
-
1: 6
3: −26
5: −38
7: −14
9: 1
11: −10
13: −1
15: 0
17: 1
19: −2
21: 29
Exercise \(\PageIndex{3}\)
Translate each sentence to a mathematical statement and then simplify.
- Find the sum of \(3\), \(7\), and \(−8\).
- Find the sum of \(−12\), \(−5\), and \(7\).
- Determine the sum of the first ten positive integers.
- Determine the sum of the integers in the set \(\{−2, −1, 0, 1, 2\}\).
- Find the difference of \(10\) and \(6\).
- Find the difference of \(10\) and \(−6\).
- Find the difference of \(−16\) and \(−5\).
- Find the difference of \(−19\) and \(7\).
- Subtract \(12\) from \(10\).
- Subtract \(−10\) from \(−20\).
- Subtract \(5\) from \(−31\).
- Subtract \(−3\) from \(27\).
- Two less than \(8\).
- Five less than \(−10\).
- Subtract \(8\) from the sum of \(4\) and \(7\).
- Subtract \(-5\) from the sum of \(10\) and \(−3\).
- Subtract \(2\) from the difference of \(8\) and \(5\).
- Subtract \(6\) from the difference of \(−1\) and \(7\).
- Mandy made a \($200\) deposit into her checking account on Tuesday. She then wrote \(4\) checks for \($50.00\), \($125.00\), \($60.00\), and \($45.00\). How much more than her deposit did she spend?
- The quarterback ran the ball three times in last Sunday’s football game. He gained \(7\) yards on one run but lost \(3\) yards and \(8\) yards on the other two. What was his total yardage running for the game?
- The revenue for a local photographer for the month is \($1,200\). His costs include a studio rental of \($600\), props costing \($105\), materials fees of \($135\), and a make-up artist who charges \($120\). What is his total profit for the month?
- An airplane flying at \(30,000\) feet lost \(2,500\) feet in altitude and then rose \(1,200\) feet. What is the new altitude of the plane?
- The temperature was \(22°\) at \(6:00\) p.m. and dropped \(26°\) by midnight. What was the temperature at midnight?
- A nurse has \(30\) milliliters of saline solution but needs \(75\) milliliters of the solution. How much more does she need?
- The width of a rectangle is \(2\) inches less than its length. If the length measures \(16\) inches, determine the width.
- The base of a triangle is \(3\) feet shorter than its height. If the height measures \(5\) feet, find the length of the base.
- Answer
-
1: \(2\)
3: \(55\)
5: \(4\)
7: \(−11\)
9: \(−2\)
11: \(−36\)
13: \(6\)
15: \(3\)
17: \(1\)
19: \($80\)
21: \($240\)
23: \(−4°\)
25: \(14\) inches
Exercise \(\PageIndex{4}\)
Find the distance between the given numbers on a number line.
- \(−3\) and \(12\)
- \(8\) and \(−13\)
- \(−25\) and \(−10\)
- \(−100\) and \(−130\)
- \(−7\) and \(−20\)
- \(0\) and \(−33\)
- \(-10\) and \(10\)
- \(−36\) and \(36\)
- The coldest temperature on earth, \(−129°\)F, was recorded in 1983 at Vostok Station, Antarctica. The hottest temperature on earth, \(136°\)F, was recorded in 1922 at Al ’Aziziyah, Libya. Calculate earth’s temperature range.
- The daily high temperature was recorded as \(91°\)F and the low was recorded as \(63°\)F. What was the temperature range for the day?
- A student earned \(67\) points on his lowest test and \(87\) points on his best. Calculate his test score range.
- On a busy day, a certain website may have \(12,500\) hits. On a slow day, it may have as few as \(750\) hits. Calculate the range of the number of hits.
- Answer
-
1: \(15\) units
3: \(15\) units
5: \(13\) units
7: \(20\) units
9: \(265°\)F
11: \(20\) points
Exercise \(\PageIndex{5}\)
Discussion Board Topics
- Share an example of adding signed numbers in a real-world application.
- Demonstrate the associative property of addition with any three real numbers.
- Show that subtraction is not commutative


