2.6: Ratio and Proportion Applications
- Page ID
- 18338
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Understand the difference between a ratio and a proportion.
- Solve proportions using cross multiplication.
- Solve applications involving proportions, including similar triangles.
Definitions
A ratio is a relationship between two numbers or quantities usually expressed as a quotient. Ratios are typically expressed using the following notation:
\(\frac{a}{b}\qquad a\:to\:b\qquad a:b\)
All of the above are equivalent forms used to express a ratio. However, the most familiar way to express a ratio is in the form of a fraction. When writing ratios, it is important to pay attention to the units. If the units are the same, then the ratio can be written without them.
Example \(\PageIndex{1}\)
Express the ratio \(12\) feet to \(48\) feet in reduced form.
Solution:
\(\begin{aligned} 12\text{ feet to }48\text{ feet} &=\frac{12\text{ feet}}{48\text{ feet}} \\ &=\color{black}{\frac{12\color{Cerulean}{\div 12}}{48\color{Cerulean}{\div 12}}} &\color{Cerulean}{Reduce.} \\ &=\frac{1}{4} \end{aligned}\)
Answer:
\(1\) to \(4\)
If the units are different, then we must be sure to include them because the ratio represents a rate.
Example \(\PageIndex{2}\)
Express the ratio \(220\) miles to \(4\) hours in reduced form.
Solution:
\(\begin{aligned} 220\text{ miles to }4\text{ hours}&=\frac{220\text{ miles}}{4\text{ hours}} \\ &=\frac{55\text{miles}}{1\text{ hour}} \\ &=55\text{ miles\hour} \end{aligned}\)
Answer:
\(55\) miles to \(1\) hours (or \(55\) miles per hour)
Rates are useful when determining unit cost, or the price of each unit. We use the unit cost to compare values when the quantities are not the same. To determine the unit cost, divide the cost by the number of units.
Example \(\PageIndex{3}\)
A local supermarket offers a pack of \(12\) sodas for $\(3.48\) on sale, and the local discount warehouse offers the soda in a \(36\)-can case for $\(11.52\). Which is the better value?
Solution:
Divide the cost by the number of cans to obtain the unit price.
| Supermarket | Discount warehouse |
|---|---|
| $\(3.4812\) cans\(=\)$\(0.29\)/can | $\(11.5236\) cans\(=\)$\(0.32\)/can |
Answer:
The supermarket sale price of $\(3.48\) for a \(12\)-pack is a better value at $\(0.29\) per can.
A proportion is a statement of equality of two ratios.
\[\frac{a}{b}=\frac{c}{d}\]
This proportion is often read “\(a\) is to \(b\) as \(c\) is to \(d\).” Here is an example of a simple proportion,
\(\frac{1}{2}=\frac{2}{4}\)
If we clear the fractions by multiplying both sides of the proportion by the product of the denominators, \(8\), then we obtain the following true statement:
\(\begin{aligned}\color{Cerulean}{8\cdot}\color{black}{\frac{1}{2}}&=\color{Cerulean}{8\cdot}\color{black}{\frac{2}{4}} \\ 4\cdot 1&=2\cdot 2\\ 4&=4 \end{aligned}\)
Given any nonzero real numbers \(a, b, c,\) and \(d\) that satisfy a proportion, multiply both sides by the product of the denominators to obtain the following:
\(\begin{aligned} \frac{a}{b}&=\frac{c}{d} \\ \color{Cerulean}{bd}\color{black}{\cdot \frac{a}{b}}&=\color{Cerulean}{bd}\color{black}{\cdot \frac{c}{d}} \\ ad&=bc \end{aligned}\)
This shows that cross products are equal, and is commonly referred to as cross multiplication.
\[\text{If }\frac{a}{b}=\frac{c}{d}\text{ then }ad=bc\]
Solving Proportions
Cross multiply to solve proportions where terms are unknown.
Example \(\PageIndex{4}\)
Solve:
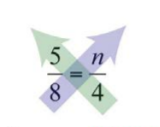
\(\frac{5}{8}=\frac{n}{4}\).
Solution:
Cross multiply and then solve for \(n\).
.png?revision=1)
Figure \(\PageIndex{1}\)
\(\begin{aligned} 5\cdot 4&=8\cdot n &\color{Cerulean}{Cross\:multiply.} \\ 20&=8n \\ \frac{20}{\color{Cerulean}{8}} &=\frac{8n}{\color{Cerulean}{8}} &\color{Cerulean}{Divide\:by\:8.} \\ \color{black}{\frac{20\color{Cerulean}{\div 4}}{8\color{Cerulean}{\div 4}}} &=n &\color{Cerulean}{Reduce.} \\ \frac{5}{2}&=n \end{aligned}\)
Answer:
\(n=\frac{5}{2}\)
Example \(\PageIndex{5}\)
Solve:
\(\frac{15}{x}=\frac{5}{6}\).
Solution:
Cross multiply then solve for \(x\).
\(\begin{aligned} \frac{15}{x}&=\frac{5}{6} \\ 15\cdot 6&=x\cdot 5 \\ 15\cdot 6&=5x \\ \frac{15\cdot 6}{\color{Cerulean}{5}}&=\frac{5x}{\color{Cerulean}{5}} \\ 3\cdot 6&=1x \\ 18&=x \end{aligned}\)
Answer:
\(x=18\)
Example \(\PageIndex{6}\)
Solve:
\(\frac{n+3}{5}=\frac{7}{2}\).
Solution:
When cross multiplying, be sure to group \(n+3\). Apply the distributive property in the next step.
\(\begin{aligned} \frac{n+3}{5}&=\frac{7}{2} &\color{Cerulean}{Cross\:multiply.} \\ (n+3)\cdot 2&=5\cdot 7 &\color{Cerulean}{Distribute.} \\ 2n+6&=35 &\color{Cerulean}{Solve.} \\ 2n+6\color{Cerulean}{-6}&=35\color{Cerulean}{-6} \\ 2n&=29 \\ \frac{2n}{\color{Cerulean}{2}}&=\frac{29}{\color{Cerulean}{2}} \\ n&=\frac{29}{2} \end{aligned}\)
Answer:
\(n=\frac{29}{2}\)
Exercise \(\PageIndex{1}\)
Solve:
\(\frac{5}{3}=\frac{3n−1}{2}\).
- Answer
-
\(n=\frac{13}{9}\)
Applications
When setting up proportions, consistency with the units of each ratio is critical. Units for the numerators should be the same and units for the denominators should also be the same.
Example \(\PageIndex{7}\)
It is claimed that \(2\) out of \(3\) dentists prefer a certain brand of toothpaste. If 600 dentists are surveyed, then how many will say they prefer that brand?
Solution:
First, identify the unknown and assign it a variable.
Let \(n\) represent the number of dentists surveyed who prefer the brand name.
Since you are looking for the number of dentists who prefer the brand name out of a total of \(600\) surveyed, construct the ratios with the number of dentists who prefer the brand in the numerator and the total number surveyed in the denominator.
\(\begin{aligned} \underline{2}=\underline{n} &\quad\color{Cerulean}{\leftarrow\:number\:of\:dentists\:who\:prefer\:the\:brand} \\ 3\:\:600&\quad\color{Cerulean}{\leftarrow\:total\:number\:of\:dentists\:surveyed} \end{aligned}\)
Cross multiply and solve for \(n\),
\(\begin{aligned} 2\cdot 600&=3\cdot n \\ \frac{2\cdot 600}{\color{Cerulean}{3}}&=\frac{3\cdot n}{\color{Cerulean}{3}} \\ 2\cdot 200&=1n \\ 400&=n \end{aligned}\)
Answer:
The claim suggests that \(400\) out of \(600\) dentists surveyed prefer the brand name.
Example \(\PageIndex{8}\)
In Tulare County, \(3\) out of every \(7\) voters said yes to Proposition 40. If \(42,000\) people voted, how many said no to Proposition 40?
Solution:
The problem gives the ratio of voters who said yes, but it asks for the number who said no.
Let \(n\) represent the number of voters who said no.
If \(3\) out of \(7\) said yes, then we can assume \(4\) out of \(7\) said no. Set up the ratios with the number of voters who said no in the numerator and the total number of voters in the denominator.
\(\begin{aligned} &\underline{4}=\:\:\:\:\underline{n}&\color{Cerulean}{\leftarrow\:voters\:who\:voted\:no} \\ &7\:\:\:\:\:\:42,000&\color{Cerulean}{\leftarrow\:total\:number\:of\:voters} \end{aligned}\)
Cross multiply and solve for \(n\).
\(\begin{aligned} 4\cdot 42,000&=7\cdot n \\ \frac{4\cdot 42,000}{\color{Cerulean}{7}}&=\frac{7\cdot n}{\color{Cerulean}{7}} \\ 24,000&=n \end{aligned}\)
Answer:
\(24,000\) voters out of \(42,000\) said no.
Example \(\PageIndex{9}\)
The sum of two integers in the ratio of \(4\) to \(5\) is \(27\). Find the integers.
Solution:
The sum of two integers is \(27\); use this relationship to avoid two variables.
Let \(n\) represent one of the integers.
Let \(27-n\) represent the other integer.
The integers are given to be in the ratio of \(4\) to \(5\). Set up the following proportion:
\(\begin{aligned} \frac{4}{5}&=\frac{n}{27-n} \\ 4\cdot (27-n)&=5\cdot n \\ 108-4n&=5n \\ 108-4n\color{Cerulean}{+4n} &=5n\color{Cerulean}{+4n} \\ 108&=9n \\ \frac{108}{\color{Cerulean}{9}}&=\frac{9n}{\color{Cerulean}{9}} \\ 12&=n \end{aligned}\)
Use \(27 − n\) to determine the other integer.
\(27-n=27-\color{OliveGreen}{12}\color{black}{=15}\)
Answer:
The integers are \(12\) and \(15\).
Exercise \(\PageIndex{2}\)
A recipe calls for \(5\) tablespoons of sugar for every \(8\) cups of flour. How many tablespoons of sugar are required for \(32\) cups of flour?
- Answer
-
\(20\) tablespoons of sugar
Similar Triangles
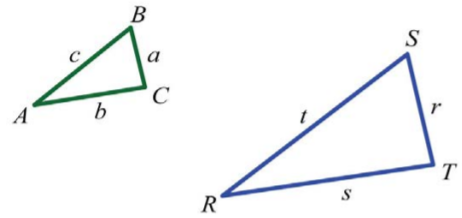
We will often encounter proportion problems in geometry and trigonometry. One application involves similar triangles, which have the same shape, but not necessarily the same size. The measures of the corresponding angles of similar triangles are equal, and the measures of the corresponding sides are proportional. Given similar triangles \(ABC\) and \(RST\),
.png?revision=1)
Figure \(\PageIndex{2}\)
We may write \(ABC ~ RST\) and conclude that all of the corresponding angles are equal. The notation indicates that angle \(A\) corresponds to angle \(R\) and that the measures of these angles are equal: \(A = R\).
.png?revision=1)
Figure \(\PageIndex{3}\)
In addition, the measures of other pairs of corresponding angles are equal: \(B = S\) and \(C = T\).
.png?revision=1)
Figure \(\PageIndex{4}\)
Use uppercase letters for angles and a lowercase letter to denote the side opposite of the given angle. Denote the proportionality of the sides as follows:
\(\frac{a}{r}=\frac{b}{s}=\frac{c}{t}\)
Example \(\PageIndex{10}\)
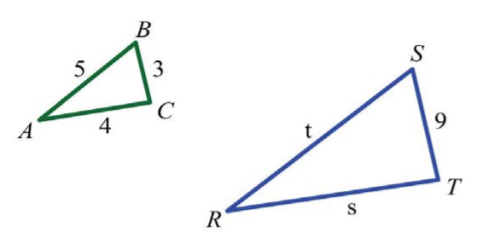
If triangle \(ABC\) is similar to \(RST\), where \(a=3, b=4, c=5,\) and \(r=9\), then find the remaining two sides.
Solution:
Draw a picture and identify the variables pictorially. Represent the remaining unknown sides by \(s\) and \(t\). Set up proportions and solve for the missing sides.
.png?revision=1)
Figure \(\PageIndex{5}\)
\(\begin{array}{c|c}{\underline{Find\:t}}&{\underline{Find\:s}}\\{\begin{aligned} \frac{5}{t}&=\frac{3}{9} \\ 5\cdot 9&=t\cdot 3 \\ \frac{5\cdot 9}{\color{Cerulean}{3}}&=\frac{t\cdot 3}{\color{Cerulean}{3}} \\ 5\cdot 3&=t \\ 15&=t \end{aligned}}&{\begin{aligned} \frac{4}{s}&=\frac{3}{9} \\ 4\cdot 9&=s\cdot 3 \\ \frac{4\cdot 9}{\color{Cerulean}{3}}&=\frac{s\cdot 3}{\color{Cerulean}{3}} \\ 4\cdot 3&=s \\ 12&=s \end{aligned}} \end{array}\)
Answer:
The two remaining sides measure \(12\) units and \(15\) units.
The reduced ratio of any two corresponding sides of similar triangles is called the scale factor. In the previous example, the ratio of the two given sides \(a\) and \(r\) is
\(\frac{3}{9}=\frac{1}{3}\)
Therefore, triangle \(ABC\) is similar to triangle \(RST\) with a scale factor of \(\frac{1}{3}\). This means that each leg of triangle \(ABC\) is \(\frac{1}{3}\) of the measure of the corresponding legs of triangle \(RST\). Also, another interesting fact is that the perimeters of similar triangles are in the same proportion as their sides and share the same scale factor.
Example \(\PageIndex{11}\)
If a triangle \(ABC\) has a perimeter of \(12\) units and is similar to \(RST\) with a scale factor of \(\frac{1}{3}\), then find the perimeter of triangle \(RST\).
Solution:
Let \(x\) represent the perimeter of triangle \(RST\).
Scale factor \(\frac{1}{3}\) implies that the perimeters are in proportion to this ratio. Set up a proportion as follows:
\(\begin{aligned} &\underline{1}=\underline{12} &\color{Cerulean}{\leftarrow\:perimeter\:of\:ABC} \\ &3\:\:\:\:\:\:x &\color{Cerulean}{\leftarrow\:perimeter\:of\:RST} \end{aligned}\)
Cross multiply and solve for \(x\).
\(\begin{aligned} 1\cdot x&=3\cdot 12 \\ x&=36 \end{aligned}\)
Answer:
The perimeter of triangle \(RST\) is \(36\) units.
Key Takeaways
- Solve proportions by multiplying both sides of the equation by the product of the denominators, or cross multiply.
- When setting up a proportion, it is important to ensure consistent units in the numerators and denominators.
- The corresponding angles of similar triangles are equal and their corresponding sides are proportional. The ratio of any two corresponding sides determines the scale factor, which can be used to solve many applications involving similar triangles.
Exercise \(\PageIndex{3}\) Ratios and Rates
Express each ratio in reduced form.
- \(100\) inches : \(250\) inches
- \(480\) pixels : \(320\) pixels
- \(96\) feet : \(72\) feet
- \(240\) miles \(4\) hours
- \(96\) feet \(3\) seconds
- \(6,000\) revolutions \(4\) minutes
- Google’s average 2008 stock price and earnings per share were $\(465.66\) and $\(14.89\), respectively. What was Google’s average price-to-earnings ratio in 2008? (Source: Wolfram Alpha)
- The F-22 Raptor has two engines that each produce \(35,000\) pounds of thrust. If the takeoff weight of this fighter jet is \(50,000\) pounds, calculate the plane’s thrust-to-weight ratio. (Source: USAF)
- A discount warehouse offers a box of \(55\) individual instant oatmeal servings for $\(11.10\). The supermarket offers smaller boxes of the same product containing \(12\) individual servings for $\(3.60\). Which store offers the better value?
- Joe and Mary wish to take a road trip together and need to decide whose car they will take. Joe calculated that his car is able to travel \(210\) miles on \(12\) gallons of gasoline. Mary calculates that her car travels \(300\) miles on \(19\) gallons. Which of their cars gets more miles to the gallon?
- Answer
-
1. \(2:5\)
3. \(4:3\)
5. \(32\) feet per second
7. \(31.27\)
9. The discount warehouse
Exercise \(\PageIndex{4}\) Solving Proportions
Solve.
- \(\frac{2}{3}=\frac{n}{150}\)
- \(\frac{7}{n}=\frac{2}{15}\)
- \(\frac{1}{3}=\frac{5}{n}\)
- \(\frac{1}{25}=\frac{6}{n}\)
- \(\frac{n}{8}=−\frac{3}{2}\)
- \(\frac{n}{3}=−\frac{5}{7}\)
- \(8=\frac{2n}{3}\)
- \(\frac{5}{n}=−30\)
- \(1=\frac{1}{n−1}\)
- \(−1=−\frac{1}{n+1}\)
- \(−\frac{40}{n}=−\frac{5}{3}\)
- \(\frac{2n+1}{3}=−\frac{3}{5}\)
- \(\frac{5}{3n+3}=\frac{2}{3}\)
- \(\frac{n+1}{2n−1}=\frac{1}{3}\)
- \(\frac{5n+7}{5}=\frac{n−1}{2}\)
- \(−\frac{2}{n+3}=\frac{n+7}{6}\)
- Find two numbers in the ratio of \(3\) to \(5\) whose sum is \(160\). (Hint: Use \(n\) and \(160 − n\) to represent the two numbers.)
- Find two numbers in the ratio of \(2\) to \(7\) whose sum is \(90\).
- Find two numbers in the ratio of \(−3\) to \(7\) whose sum is \(80\).
- Find two numbers in the ratio of \(−1\) to \(3\) whose sum is \(90\).
- A larger integer is \(5\) more than a smaller integer. If the two integers have a ratio of \(6\) to \(5\) find the integers.
- A larger integer is \(7\) less than twice a smaller integer. If the two integers have a ratio of \(2\) to \(3\) find the integers.
- Answer
-
1. \(n=100\)
3. \(n=15\)
5. \(n=−12\)
7. \(n=12\)
9. \(n=2\)
11. \(n=24\)
13. \(n=\frac{3}{2}\)
15. \(n=−\frac{19}{5}\)
17. \(60, 100\)
19. \(−60, 140\)
21. \(25, 30\)
Exercise \(\PageIndex{5}\) Solving Proportions
Given the following proportions, determine each ratio, \(x:y\).
- \(\frac{x}{3}=\frac{y}{4}\)
- \(\frac{x−2y}{3}=−\frac{3y}{5}\)
- \(\frac{2x+4y}{2x−4y}=\frac{3}{2}\)
- \(\frac{x+y}{x−y}=\frac{3}{5}\)
- Answer
-
1. \(\frac{3}{4}\)
3. \(10\)
Exercise \(\PageIndex{6}\) Applications
Set up a proportion and then solve.
- If \(4\) out of every \(5\) voters support the governor, then how many of the \(1,200\) people surveyed support the governor?
- If \(1\) out of every \(3\) voters surveyed said they voted yes on Proposition 23, then how many of the \(600\) people surveyed voted yes?
- Out of \(460\) students surveyed, the ratio to support the student union remodel project was \(3\) to \(5\). How many students were in favor of the remodel?
- An estimated \(5\) out of \(7\) students carry credit card debt. Estimate the number of students that carry credit card debt out of a total of \(14,000\) students.
- If the ratio of female to male students at the college is \(6\) to \(5\), then determine the number of male students out of \(11,000\) total students.
- In the year 2009 it was estimated that there would be \(838\) deaths in the United States for every \(100,000\) people. If the total US population was estimated to be \(307,212,123\) people, then how many deaths in the United States were expected in 2009? (Source: CIA World Factbook)
- In the year 2009 it was estimated that there would be \(1,382\) births in the United States for every \(100,000\) people. If the total US population was estimated to be \(307,212,123\) people, then how many births in the United States were expected in 2009? (Source: CIA World Factbook)
- If \(2\) out of every \(7\) voters approve of a sales tax increase then determine the number of voters out of the \(588\) surveyed who do not support the increase.
- A recipe calls for \(1\) cup of lemon juice to make \(4\) cups of lemonade. How much lemon juice is needed to make \(2\) gallons of lemonade?
- The classic “Shirley Temple” cocktail requires \(1\) part cherry syrup to \(4\) parts lemon-lime soda. How much cherry syrup is needed to mix the cocktail given a \(12\)-ounce can of lemon-lime soda?
- A printer prints \(30\) pages in \(1\) minute. How long will it take to print a \(720\)-page booklet?
- A typist can type \(75\) words per minute. How long will it take to type \(72\) pages if there are approximately \(300\) words per page?
- On a particular map, every \(\frac{1}{16}\) inch represents \(1\) mile. How many miles does \(3\frac{1}{2}\) inches represent?
- On a graph every \(1\) centimeter represents \(100\) feet. What measurement on the map represents one mile?
- A candy store offers mixed candy at $\(3.75\) for every half-pound. How much will \(2.6\) pounds of candy cost?
- Mixed nuts are priced at $\(6.45\) per pound. How many pounds of mixed nuts can be purchased with $\(20.00\)?
- Corn at the farmers market is bundled and priced at $\(1.33\) for \(6\) ears. How many ears can be purchased with $\(15.00\)?
- If \(4\) pizzas cost $\(21.00\), then how much will \(16\) pizzas cost?
- A sweetened breakfast cereal contains \(110\) calories in one \(\frac{3}{4}\)-cup serving. How many calories are in a \(1\frac{7}{8}\)-cup serving?
- Chicken-flavored rice contains \(300\) calories in each \(2.5\)-ounce serving. How many calories are in a \(4\)-ounce scoop of chicken-flavored rice?
- A \(200\)-pound man would weigh about \(33.2\) pounds on the moon. How much will a \(150\)-pound man weigh on the moon?
- A \(200\)-pound man would weigh about \(75.4\) pounds on Mars. How much will a \(150\)-pound man weigh on Mars?
- There is a \(1\) out of \(6\) chance of rolling a \(1\) on a six-sided die. How many times can we expect a \(1\) to come up in \(360\) rolls of the die?
- There is a \(1\) out of \(6\) chance of rolling a \(7\) with two six-sided dice. How many times can we expect a \(7\) to come up in \(300\) rolls?
- The ratio of peanuts to all nuts in a certain brand of packaged mixed nuts is \(3\) to \(5\). If the package contains \(475\) nuts, then how many peanuts can we expect?
- A mixed bag of marbles is packaged with a ratio of \(6\) orange marbles for every \(5\) red marbles. If the package contains \(216\) orange marbles, then how many red marbles can we expect?
- A graphic designer wishes to create a \(720\)-pixel-wide screen capture. If the width to height ratio is to be \(3:2\), then to how many pixels should he set the height?
- If a video monitor is produced in the width to height ratio of \(16:9\) and the width of the monitor is \(40\) inches, then what is the height?
- Answer
-
1. \(960\) people
3. \(276\) students
5. \(5,000\) male students
7. \(4,245,672\) births
9. \(8\) cups of lemon juice
11. \(24\) minutes
13. \(56\) miles
15. $\(19.50\)
17. \(66\) ears
19. \(275\) calories
21. \(24.9\) pounds
23. \(60\) times
25. \(285\) peanuts
27. \(480\) pixels
Exercise \(\PageIndex{7}\) Similar Triangles
If triangle \(ABC\) is similar to triangle \(RST\), find the remaining two sides given the information.
- \(a=6, b=8, c=10,\) and \(s=16\)
- \(b=36, c=48, r=20,\) and \(t=32\)
- \(b=2, c=4, r=6,\) and \(s=4\)
- \(b=3, c=2, r=10,\) and \(t=12\)
- \(a=40, c=50, s=3,\) and \(t=10\)
- \(c=2, r=7, s=9,\) and \(t=4\)
- At the same time of day, a tree casts a \(12\)-foot shadow while a \(6\)-foot man casts a \(3\)-foot shadow. Estimate the height of the tree.
- At the same time of day, a father and son, standing side by side, cast a \(4\)-foot and \(2\)-foot shadow, respectively. If the father is \(6\) feet tall, then how tall is his son?
- If the \(6-8-10\) right triangle \(ABC\) is similar to \(RST\) with a scale factor of \(\frac{2}{3}\), then find the perimeter of triangle \(RST\).
- If the \(3-4-5\) right triangle \(ABC\) is similar to \(RST\) with a scale factor of \(5\), then find the perimeter of triangle \(RST\).
- An equilateral triangle with sides measuring \(6\) units is similar to another with scale factor \(3:1\). Find the length of each side of the unknown triangle.
- The perimeter of an equilateral triangle \(ABC\) measures \(45\) units. If triangle \(ABC ~ RST\) and \(r=20\), then what is the scale factor?
- The perimeter of an isosceles triangle \(ABC\), where the two equal sides each measure twice that of the base, is \(60\) units. If the base of a similar triangle measures \(6\) units, then find its perimeter.
- The perimeter of an isosceles triangle ABC measures \(11\) units and its two equal sides measure \(4\) units. If triangle \(ABC\) is similar to triangle \(RST\) and triangle \(RST\) has a perimeter of \(22\) units, then find all the sides of triangle \(RST\).
- A \(6-8-10\) right triangle \(ABC\) is similar to a triangle \(RST\) with perimeter \(72\) units. Find the length of each leg of triangle \(RST\).
- The perimeter of triangle \(ABC\) is \(60\) units and \(b=20\) units. If \(ABC ~ RST\) and \(s=10\) units, then find the perimeter of triangle \(RST\).
- Answer
-
1. \(t = 20, r = 12\)
3. \(a = 3, t = 8\)
5. \(r = 8, b = 15\)
7. \(24\) feet
9. \(36\) units
11. \(2\) units
13. \(30\) units
15. \(r = 18\) units, \(s = 24\) units, \(t = 30\) units
Exercise \(\PageIndex{8}\) Discussion Board Topics
- What is the golden ratio and where does it appear?
- Research and discuss the properties of similar triangles.
- Discuss the mathematics of perspective.
- Research and discuss the various aspect ratios that are available in modern media devices.
- Answer
-
1. Answers may vary
3. Answers may vary


