1.1: Review of Real Numbers and Absolute Value
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Review the set of real numbers.
- Review the real number line and notation.
- Define the geometric and algebraic definition of absolute value.
Real Numbers
Algebra is often described as the generalization of arithmetic. The systematic use of variables1, letters used to represent numbers, allows us to communicate and solve a wide variety of real-world problems. For this reason, we begin by reviewing real numbers and their operations.
A set2 is a collection of objects, typically grouped within braces
The three periods (…) are called an ellipsis and indicate that the numbers continue without bound. A subset4, denoted
A set with no elements is called the empty set7 and has its own special notation:
Rational numbers8, denoted
The vertical line | inside the braces reads, “such that” and the symbol
The set of integers is a subset of the set of rational numbers,
Irrational numbers10 are defined as any numbers that cannot be written as a ratio of two integers. Nonterminating decimals that do not repeat are irrational. For example,
Finally, the set of real numbers11, denoted

The set of even integers12 is the set of all integers that are evenly divisible by
The set of odd integers13 is the set of all nonzero integers that are not evenly divisible by
A prime number14 is an integer greater than
Any integer greater than

Therefore, the prime factorization18 of
Example
Determine the prime factorization of
Solution
Begin by writing
Since the prime factorization is unique, it does not matter how we choose to initially factor the number; the end result will be the same.
Answer:
A fraction19 is a rational number written as a quotient, or ratio, of two integers a and b where

The integer above the fraction bar is called the numerator20 and the integer below is called the denominator21. Two equal ratios expressed using different numerators and denominators are called equivalent fractions22. For example,
Consider the following factorizations of
The numbers
Dividing
Finding equivalent fractions where the numerator and denominator are relatively prime26, or have no common factor other than
Common factors are listed in bold, and we see that the greatest common factor is
Example
Reduce to lowest terms:
Solution
A quick way to find the GCF of the numerator and denominator requires us to first write each as a product of primes. The GCF will be the product of all the common prime factors.
In this case, the product of the common prime factors is
We can convert the improper fraction
Answer:
Recall the relationship between multiplication and division:
.png?revision=1&size=bestfit&width=540&height=83)
In this case, the dividend29
This demonstrates that zero divided by any nonzero real number must be zero. Now consider a nonzero number divided by zero:
Zero times anything is zero and we conclude that there is no real number such that
We are left to consider the case where the dividend and divisor are both zero.
Here, any real number seems to work. For example,
In this course, we state that
The Number Line and Notation
A real number line34, or simply number line, allows us to visually display real numbers by associating them with unique points on a line. The real number associated with a point is called a coordinate35. A point on the real number line that is associated with a coordinate is called its graph36. To construct a number line, draw a horizontal line with arrows on both ends to indicate that it continues without bound. Next, choose any point to represent the number zero; this point is called the origin37.
Positive real numbers lie to the right of the origin and negative real numbers lie to the left. The number zero
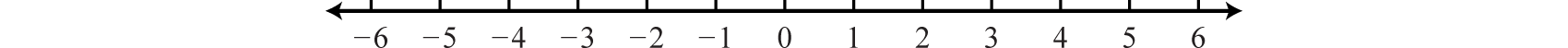
As illustrated below, the scale need not always be one unit. In the first number line, each tick mark represents two units. In the second, each tick mark represents
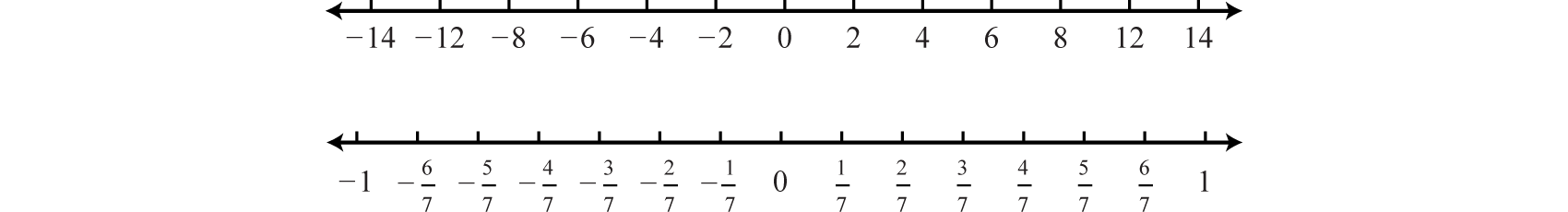
The graph of each real number is shown as a dot at the appropriate point on the number line. A partial graph of the set of integers

Example
Graph the following set of real numbers:
Solution
Graph the numbers on a number line with a scale where each tick mark represents
Answer:
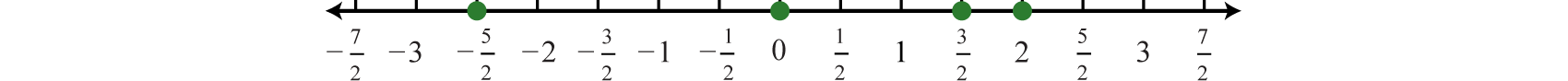
The opposite38 of any real number a is −a. Opposite real numbers are the same distance from the origin on a number line, but their graphs lie on opposite sides of the origin and the numbers have opposite signs.
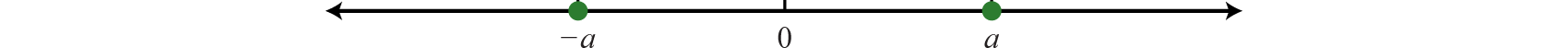
Given the integer

Therefore, we say that the opposite of
Example
Calculate:
Solution
Here we apply the double-negative within the innermost parentheses first.
Answer:
In general, an odd number of sequential negative signs results in a negative value and an even number of sequential negative signs results in a positive value.
When comparing real numbers on a number line, the larger number will always lie to the right of the smaller one. It is clear that
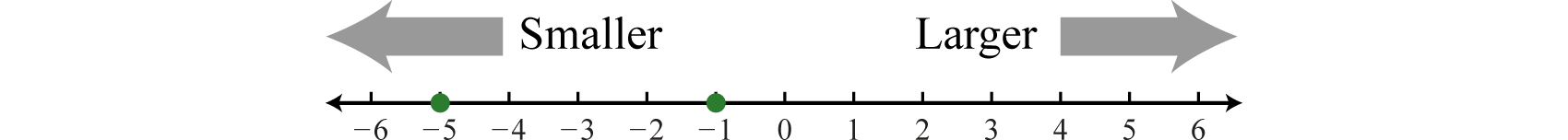
We use symbols to help us efficiently communicate relationships between numbers on the number line.
The relationship between the integers40 in the previous illustration can be expressed two ways as follows:
or
The symbols
In addition, the “or equal to” component of an inclusive inequality allows us to correctly write the following:
The logical use of the word “or” requires that only one of the conditions need be true: the “less than” or the “equal to.”
Example
Fill in the blank with
Solution
Use

Answer:
An algebraic inequality43, such as
To express the solution graphically, draw a number line and shade in all the values that are solutions to the inequality. This is called the graph of the solution set45. Interval and set notation follow:
"x is greater than or equal to

In this example, there is an inclusive inequality, which means that the lower-bound
"x is less than

Strict inequalities imply that solutions may get very close to the boundary point, in this case
Interval notation is textual and is determined after graphing the solution set on a number line. The numbers in interval notation should be written in the same order as they appear on the number line, with smaller numbers in the set appearing first. Set notation, sometimes called set-builder notation, allows us to describe the set using familiar mathematical notation. For example,
Here,
Example
Graph the solution set and give the interval and set notation equivalents:
Solution
Use an open dot at
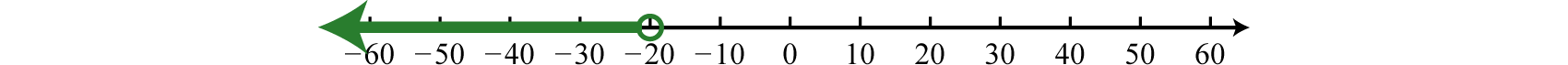
Answer:
Interval notation:
A compound inequality48 is actually two or more inequalities in one statement joined by the word “and” or by the word “or”. Compound inequalities with the logical “or” require that either condition must be satisfied. Therefore, the solution set of this type of compound inequality consists of all the elements of the solution sets of each inequality. When we join these individual solution sets it is called the union49, denoted
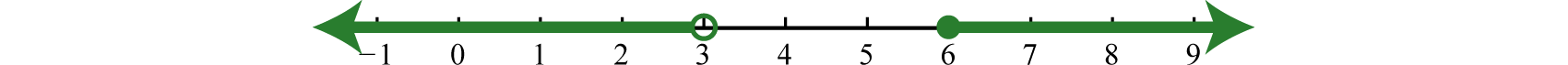
An inequality such as,
reads, “negative one is less than or equal to x and x is less than three.” This is actually a compound inequality because it can be decomposed as follows:
The logical “and” requires that both conditions must be true. Both inequalities will be satisfied by all the elements in the intersection50, denoted
Example
Graph and give the interval notation equivalent:
Solution
Determine the intersection, or overlap, of the two solution sets to
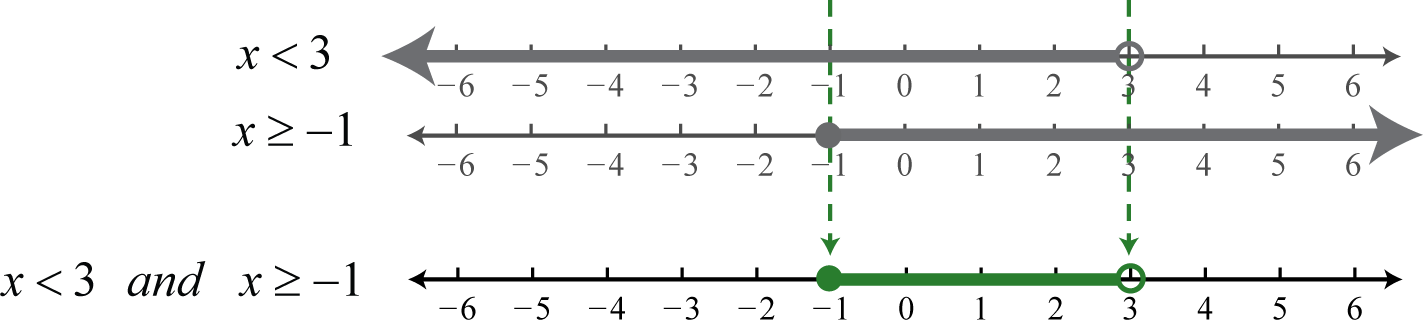
Here,
Answer:
Interval notation:
In this text, we will often point out the equivalent notation used to express mathematical quantities electronically using the standard symbols available on a keyboard.
Many calculators, computer algebra systems, and programming languages use the notation presented above, in quotes.
Absolute Value
The absolute value51 of a real number a, denoted
Both
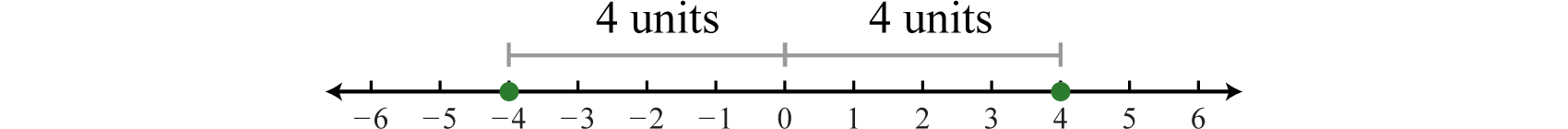
Also, it is worth noting that,
The algebraic definition of the absolute value of a real number a follows:
This is called a piecewise definition52. The result depends on the quantity a. If a is nonnegative, as indicated by the inequality
At this point, we can determine what real numbers have certain absolute values.
Example
Determine the values represented by \(x: | x |=6\).
Solution
Think of a real number whose distance to the origin is 6 units. There are two solutions: the distance to the right of the origin and the distance to the left of the origin, namely
Answer:
x=±6
Example
Determine the values represented by \(x: | x |=−6\).
Solution
Here we wish to find a value where the distance to the origin is negative. Since negative distance is not defined, this equation has no solution. Use the empty set
Answer:
The absolute value can be expressed textually using the notation abs(a). We often encounter negative absolute values, such as
Try not to confuse this with the double negative property, which states that
Example
Simplify:
Solution
First, find the absolute value of
Answer:
Key Takeaways
- Algebra is often described as the generalization of arithmetic. The systematic use of variables, used to represent real numbers, allows us to communicate and solve a wide variety of real-world problems. Therefore, it is important to review the subsets of real numbers and their properties.
- The number line allows us to visually display real numbers by associating them with unique points on a line.
- Special notation is used to communicate equality and order relationships between numbers on a number line.
- The absolute value of a real number is defined geometrically as the distance between zero and the graph of that number on a number line. Alternatively, the absolute value of a real number is defined algebraically in a piecewise manner. If a real number a is nonnegative, then the absolute value will be that number a. If a is negative, then the absolute value will be the opposite of that number, −a.
Exercise
Use set notation to list the described elements.
- Every other positive odd number up to
- Every other positive even number up to
- The even prime numbers.
- Rational numbers that are also irrational.
- The set of negative integers.
- The set of negative even integers.
- Three consecutive odd integers starting with
- Three consecutive even integers starting with
- Answer
-
1.
3.
5.
7.
Exercise
Determine the prime factorization of the given composite number.
- Answer
-
1.
3.
5.
Exercise
Reduce to lowest terms.
- Answer
-
1.
3.
5.
7.
9.
Exercise
Graph the following sets of numbers.
- Answer
-

Figure 
Figure 
Figure
Exercise
Simplify.
- Answer
-
1.
3.
5.
Exercise
Fill in the blank with
- Answer
-
1.
3.
5.
7.
Exercise
True or False.
- Any integer is a rational number.
- The constant
- Answer
-
1. True
3. False
5. True
Exercise
Graph the solution set and give the interval notation equivalent.
- Answer
-
1.
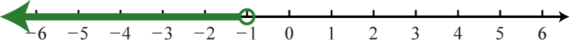
Figure 3.

Figure 5.

Figure 7.

Figure 9.

Figure 11.

Figure 13.
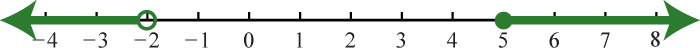
Figure 15.

Figure
Exercise
Write an equivalent inequality.
- All real numbers less than
- All real numbers greater than or equal to
- All real numbers less than
- All real numbers less than zero and greater than
- All real numbers less than or equal to
- All real numbers between
- Answer
-
1.
3.
5.
Exercise
Determine the inequality given the answers expressed in interval notation.
- Answer
-
1.
3.
5.
7.
9.
11.
Exercise
Simplify.
- Answer
-
1.
3.
5.
7.
9.
11.
Exercise
Determine the values represented by a.
- Answer
-
1.
3.
5.
Exercise
- Research and discuss the origins and evolution of algebra.
- Research and discuss reasons why algebra is a required subject today.
- Solution sets to inequalities can be expressed using a graph, interval notation, or set notation. Discuss the merits and drawbacks of each method. Which do you prefer?
- Research and discuss the Fundamental Theorem of Algebra. Illustrate its idea with an example and share your results.
- Answer
-
1. Answer may vary
3. Answer may vary
Footnotes
1Letters used to represent numbers.
2Any collection of objects.
3An object within a set.
4A set consisting of elements that belong to a given set.
5The set of counting numbers:
6The set of natural numbers combined with zero:
7A subset with no elements, denoted
8Numbers of the form
9Notation used to describe a set using mathematical symbols.
10Numbers that cannot be written as a ratio of two integers.
11The set of all rational and irrational numbers.
12Integers that are divisible by
13Nonzero integers that are not divisible by
14Integer greater than
15Integers greater than
16Any combination of factors, multiplied together, resulting in the product.
17Any of the numbers that form a product.
18The unique factorization of a natural number written as a product of primes.
19A rational number written as a quotient of two integers:
20The number above the fraction bar.
21The number below the fraction bar. \
22Two equal fractions expressed using different numerators and denominators.
23A factor that is shared by more than one real number.
24The process of dividing out common factors in the numerator and the denominator.
25The process of finding equivalent fractions by dividing the numerator and the denominator by common factors.
26Numbers that have no common factor other than
27Finding equivalent fractions where the numerator and the denominator share no common integer factor other than
28The largest shared factor of any number of integers.
29A number to be divided by another number.
30The number that is divided into the dividend.
31The result of division.
32A quotient such as
33A quotient such as
34A line that allows us to visually represent real numbers by associating them with points on the line.
35The real number associated with a point on a number line.
36A point on the number line associated with a coordinate.
37The point on the number line that represents zero.
38Real numbers whose graphs are on opposite sides of the origin with the same distance to the origin.
39The opposite of a negative number is positive:
40The set of positive and negative whole numbers combined with zero:
41Express ordering relationships using the symbol
42Use the symbol
43Algebraic expressions related with the symbols
44Values that can be used in place of the variable to satisfy the given condition.
45Solutions to an algebraic expression expressed on a number line.
46The symbol
47The symbol
48Two or more inequalities in one statement joined by the word “and” or by the word “or.”
49The set formed by joining the individual solution sets indicated by the logical use of the word “or” and denoted with the symbol
50The set formed by the shared values of the individual solution sets that is indicated by the logical use of the word “and,” denoted with the symbol
51The absolute value of a number represents the distance from the graph of the number to zero on a number line.
52A definition that changes depending on the value of the variable.


