2.1: Real Numbers, Linear Inequalities, and Interval Notation

Last updated
Save as PDF

Page ID: 87888

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Real Numbers

Algebra is often described as the generalization of arithmetic. The systematic use of variables, letters used to represent numbers, allows us to communicate and solve a wide variety of real-world problems. For this reason, we begin by reviewing real numbers and their operations.

A set is a collection of objects, typically grouped within braces, $\{ \}$, where each object is called an element. When studying mathematics, we focus on special sets of numbers.

\[ \begin{align*} \mathbb { N } &= \underbrace{\{ 1,2,3,4,5 , \dots \}}_{\color{Cerulean}{Natural\: Numbers}} \\[4pt] W &= \underbrace{ \{ 0 , 1,2,3,4,5 , \dots \}}_{\color{Cerulean}{Whole\: Numbers}} \\[4pt] \mathbb{Z} &= \underbrace{ \{\dots ,-3,-2,-1,0,1,2,3,\dots\}}_{\color{Cerulean}{Integers}} \end{align*}\]

The three periods (…) are called an ellipsis and indicate that the numbers continue without bound. A subset, denoted $\subseteq$, is a set consisting of elements that belong to a given set. Notice that the sets of natural and whole numbers are both subsets of the set of integers and we can write:

$\mathbb { N } \subseteq \mathbb{Z}$ and $W \subseteq \mathbb{Z}$

A set with no elements is called the empty set and has its own special notation:

$\{\:\:\:\}=\varnothing\: \color{Cerulean}{Empty\: Set}$

Rational numbers, denoted $\mathbb{Q}$, are defined as any number of the form $\frac { a } { b }$ where a and b are integers and b is nonzero. We can describe this set using set notation:

$\mathbb { Q } = \left\{ \frac { a } { b } | a , b \in \mathbb { Z } , b \neq 0 \right\} \color{Cerulean}{Rational\: Numbers}$

The vertical line | inside the braces reads, “such that” and the symbol $\in$ indicates set membership and reads, “is an element of.” The notation above in its entirety reads, “the set of all numbers $\frac{a}{b}$ such that a and b are elements of the set of integers and b is not equal to zero.” Decimals that terminate or repeat are rational. For example,

$0.05=\frac{5}{100}$ and $0.\overline{6}=0.6666…=\frac{2}{3} $

The set of integers is a subset of the set of rational numbers, $\mathbb{Z}\subseteq\mathbb{Q}$, because every integer can be expressed as a ratio of the integer and 1. In other words, any integer can be written over 1 and can be considered a rational number. For example,

$7=\frac{7}{1}$

Irrational numbers are defined as any numbers that cannot be written as a ratio of two integers. Non-terminating decimals that do not repeat are irrational. For example,

$π=3.14159…$ and $\sqrt{2}=1.41421…$

Finally, the set of real numbers, denoted $\mathbb{R}$, is defined as the set of all rational numbers combined with the set of all irrational numbers. Therefore, all the numbers defined so far are subsets of the set of real numbers. In summary,

Image of set and subsets of real numbers — Figure $\PageIndex{1}$: Real Numbers

The set of even integers is the set of all integers that are evenly divisible by $2$. We can obtain the set of even integers by multiplying each integer by $2$.

$\{\dots, −6,−4,−2, 0, 2, 4, 6,\dots\} \color{Cerulean}{Even\: Integers}$

The set of odd integers is the set of all nonzero integers that are not evenly divisible by $2$.

$\{\dots,−5,−3,−1, 1, 3, 5,\dots\} \color{Cerulean}{Odd\: Integers}$

A prime number is an integer greater than $1$ that is divisible only by $1$ and itself. The smallest prime number is $2$ and the rest are necessarily odd.

$\{2, 3, 5, 7, 11, 13, 17, 19, 23,\dots\} \color{Cerulean}{Prime\: Numbers}$

Any integer greater than $1$ that is not prime is called a composite number and can be uniquely written as a product of primes. When a composite number, such as $42$, is written as a product, $42=2⋅21$, we say that $2⋅21$ is a factorization of $42$ and that $2$ and $21$ are factors. Note that factors divide the number evenly. We can continue to write composite factors as products until only a product of primes remains.

Image of prime factorization of 42 — Figure $\PageIndex{2}$: Prime Factorization of the number $42$

Therefore, the prime factorization of $42$ is $2⋅3⋅7$.

Example $\PageIndex{1}$

Determine the prime factorization of $210$.

Solution

Begin by writing $210$ as a product with $10$ as a factor. Then continue factoring until only a product of primes remains.

$210=10⋅21$

$=2⋅5⋅3⋅7$

$=2⋅3⋅5⋅7$

Since the prime factorization is unique, it does not matter how we choose to initially factor the number; the end result will be the same.

Answer: $2⋅3⋅5⋅7$

The Number Line and Notation

A real number line, or simply number line, allows us to visually display real numbers and solution sets to inequalities.

Positive real numbers lie to the right of the origin and negative real numbers lie to the left. The number zero $0$ is neither positive nor negative. Typically, each tick mark represents one unit.

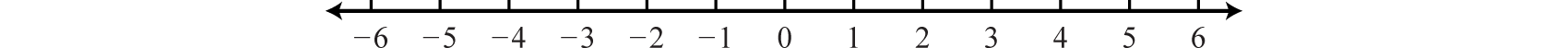
Image of real number line — Figure $\PageIndex{3}$

As illustrated below, the scale need not always be one unit. In the first number line, each tick mark represents two units. In the second, each tick mark represents $\dfrac{1}{7}$:

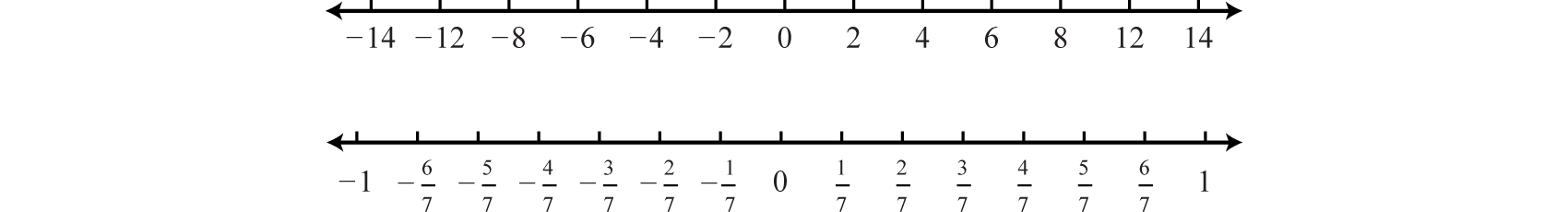
Images of real number lines with different units — Figure $\PageIndex{4}$

Graph Inequalities on the Number Line

What number would make the inequality $x>3$ true? Are you thinking, "$x$ could be four"? That’s correct, but $x$ could be 6, too, or 37, or even 3.001. Any number greater than three is a solution to the inequality $x>3$. We show all the solutions to the inequality $x>3$ on the number line by shading in all the numbers to the right of three, to show that all numbers greater than three are solutions. Because the number three itself is not a solution, we put an open parenthesis at three.

We can represent inequalities using interval notation or set notation. In this text, we will use interval notation. There is no upper end to the solution to this inequality. In interval notation, we express $x>3$ as $(3,\infty)$. The symbol $\infty$ is read as “infinity.” It is not an actual number.

Before we begin, let us review the conventions of interval notation:

The smallest term from the interval is written first.
The largest term in the interval is written second, following a comma.
Parentheses, $($ or $)$, are used to signify that an endpoint is not included, called exclusive.
Brackets, $[$ or $]$, are used to indicate that an endpoint is included, called inclusive.

Some use parentheses and brackets when graphing solution sets on a number line. Others use open circles to denote when an endpoint is not included and a closed circle when an endpoint is included.

See Figure $\PageIndex{5}$ for a summary of interval notation.

Table showing inequalities, their description, and associated interval notation and graphs. — Figure $\PageIndex{5}$: Summary of interval notation.

Example $\PageIndex{2}$

Graph each inequality on the number line and write in interval notation.

$x\geq −3$
$x\leq −\frac{3}{5}$

Solution

	$ x \geq -3 $
Shade to the right of $−3$, and put a bracket at $−3$.	$Example2.1.jpg$
Write in interval notation.	$ [-3, \infty) $

	$ x \leq -\dfrac{3}{5} $
Shade to the left of $−\frac{3}{5}$, and put a bracket at $−\frac{3}{5}$.	$Example2.2.jpg$
Write in interval notation.	$ \bigg( -\infty, \dfrac{3}{5}\bigg] $

You Try $\PageIndex{1}$

Graph each inequality on the number line and write in interval notation:

$x\leq −4$
$0.5 \leq x$
$−\frac{2}{3} > x$

Answer

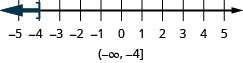
$The graph of the inequality x is less than or equal to negative 4 is indicated on a number line with a right bracket at negative 4 and shading to the left. The solution in interval notation is the interval from negative infinity to negative 4 enclosed within an left parenthesis and right bracket.$

$The graph of the inequality x is greater than or equal to 0.5 is indicated on a number line with a left bracket at 0.5 and shading to the right. The solution in interval notation is the interval from 0.5 to infinity enclosed within a left bracket and right parenthesis.$

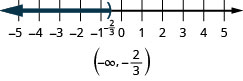
$The graph of the inequality x is less than negative two-thirds is indicated on a number line with a right parenthesis at negative two-thirds and shading to the left. The solution in interval notation is the interval from negative infinity to negative two-thirds enclosed within parentheses.$

What numbers are greater than two but less than five? Are you thinking say, $2.5,\space 3,\space 3\frac{2}{3},\space 4,\space 4,\space 99$? We can represent all the numbers between two and five with the inequality $2<x<5$. We can show $2<x<5$ on the number line by shading all the numbers between two and five. Again, we use the parentheses to show the numbers two and five are not included. See Figure $\PageIndex{6}$.

The graph of the inequality 2 is less than x which is less than 5 shows open circles a 2 and 5 and shading in between. — Figure $\PageIndex{6}$

You Try $\PageIndex{2}$

Graph each inequality on the number line and write in interval notation:

$−2<x<1$
$−5\leq x<−4$
$1\leq x\leq 4.25$

Answer

Interval notation: $(-2,1)$

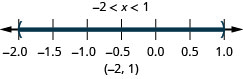
$Negative 2 is less x which is less than 1. There are open circles at negative 2 and 1 and shading between negative 2 and 1 on the number line. Put parentheses at negative 2 and 1. Write in interval notation.$

Interval notation: $[-5,4)$

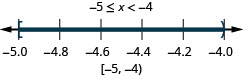
$Negative 5 is less than or equal to x which is less than negative 4. There is a closed circle at negative 6 and an open circle at negative 4 and shading between negative 5 and negative 4 on the number line. Put a bracket at negative 5 and a parenthesis at negative 4. Write in interval notation.$

Interval notation: $[1,4.25]$

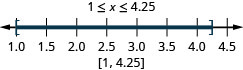
$1 is less than or equal to x which is less than 4.25. There is closed circle at 1 and a closed circle at 4.25 and shading between 1 and 4.25 on the number line. Put brackets at 1 and 4.25. Write in interval notation.$

Linear Inequalities

A linear inequality is a mathematical statement that relates a linear expression as either less than or greater than another. The following are some examples of linear inequalities, all of which are solved in this section:

Table $\PageIndex{1}$
$5 x + 7 < 22$	$- 2 ( x + 8 ) + 6 \geq 20$	$- 2 ( 4 x - 5 ) < 9 - 2 ( x - 2 )$

A solution to a linear inequality is any real number that will produce a true statement when substituted in for the variable. We graph the solution set on a number line and/or express the solution using interval notation. In the case that there is no solution to the inequality we indicate the solution using the empty set, $\{\:\:\:\} \text{ or }\varnothing\: $.

Example $\PageIndex{3}$

Are $x=−4$ and $x=6$ solutions to $5x+7<22$?

Solution

Substitute the values in for $x$, simplify, and check to see if we obtain a true statement.

Table $\PageIndex{2}$
Check $x=−4$	Check $x=6$
$\begin{array} { r } { 5 ( \color{Cerulean}{- 4}\color{Black}{ )} + 7 < 22 } \\ { - 20 + 7 < 22 } \\ { - 13 < 22 } \:\:\color{Cerulean}{✓} \end{array}$	$\begin{array} { c } { 5 ( \color{Cerulean}{6} \color{Black}{)} + 7 < 22 } \\ { 30 + 7 < 22 } \\ { 37 < 22 } \:\:\color{red}{✗} \end{array}$

Answer:

$x=−4$ is a solution and $x=6$ is not

To solve a linear inequality, one must isolate the variable on one side of the inequality symbol. If we add or subtract on both sides of an inequality, we will have an equivalent inequality.

Adding or Subtracting the Same Quantity from Both Sides of an Inequality

Let $a$ and $b$ be real numbers with \[a < b \nonumber \]
If $c$ is any real number, then \[a + c<b+ c \nonumber \]and\[a−c<b−c \nonumber \]That is, adding or subtracting the same amount from both sides of an inequality produces an equivalent inequality (does not change the solution).

There is more than one way to denote the solution to an inequality on a number line, as seen in the next example.

Example $\PageIndex{4}$

Solve for $x: \quad x-2 ≤ 7$. Sketch the solution on the real line, then use interval notation to describe your solution.

Solution

To “undo” subtracting $2$, we add $2$ to both sides of the inequality.

\[\begin{aligned} x-2 &\leq 7 & & \color {Red} \text { Original inequality. } \\ x-2+2 &\leq 7+2 & & \color {Red} \text { Add } 2 \text { to both sides. } \\ x &\leq 9 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

To shade the real numbers less than or equal to $9$, we shade the number $9$ and all real numbers to the left of $9$.

$Image of number line including 9 with arrow shading to the left$

Using interval notation, the solution is $(-\infty, 9]$.

When drawing the endpoints for a solution on a number line, one may use brackets or filled in circles which indicate that the number is a solution. A parenthesis or open circle indicates that the number is not a solution.

You Try $\PageIndex{3}$

Use interval notation to describe the solution of: $x−7 < −8$.

Answer: $(-\infty,-1)$

If we multiply or divide both sides of an inequality by a positive number, we have an equivalent inequality.

Multiplying or Dividing by a Positive Number on Both Sides of an Inequality

Let $a$ and $b$ be real numbers with $a<b$. If $c$ is a real positive number, then \[a c<b c \nonumber \]and\[\dfrac{a}{c}<\dfrac{b}{c} \nonumber \]

Example $\PageIndex{5}$

Solve for $x : \quad 3 x \leq-9$ Sketch the solution on the real line and state the solution in interval notation.

Solution

To “undo” multiplying by $3$, divide both sides of the inequality by $3$. Because we are dividing both sides by a positive number, we do not reverse the inequality sign.

\[\begin{aligned} 3x & \leq -9 & & \color {Red} \text { Original inequality. } \\ \dfrac{3x}{3} & \leq \dfrac{-9}{3} & & \color {Red} \text { Divide both sides by } 3. \\ x & \leq -3 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Shade the real numbers less than or equal to $-3$.

$Image of number line including -3 with arrow shading to the left$

The solution in interval notaiton is $(-\infty,-3]$.

You Try $\PageIndex{4}$

Use interval notation to describe the solution of: \[2 x>-8 \nonumber \]

Answer: $(-4, \infty)$

When you multiply both sides of an inequality by a negative number, you must reverse the inequality sign to keep the statement true.

Multiplying or Dividing by a Negative Number

Let $a$ and $b$ be real numbers with $a<b$. If $c$ is a real negative number, then \[a c>b c \nonumber \] and \[\dfrac{a}{c}>\dfrac{b}{c} \nonumber \]That is, when multiplying or dividing both sides of an inequality by a negative number, you must reverse the inequality sign.

Example $\PageIndex{6}$

Solve for $x: \quad −2x<4$. Sketch the solution on the real line, then use interval notation to describe your solution.

Solution

To “undo” multiplying by $−2$, divide both sides by $−2$. Because we are dividing both sides by a negative number, we reverse the inequality sign.

\[\begin{aligned} -2 x&< 4 & & \color {Red} \text { Original inequality. } \\ \dfrac{-2x}{-2}&> \dfrac{4}{-2} & & \color {Red} \text { Divide both sides by }-2 \\ x&> -2 & & \color {Red} \text { Reverse the inequality sign. } \\ x&> -2 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Shade the real numbers greater than $−2$.

$Image of number line excluding -2 with arrow shading to the right$

Using interval notation, the solution is $(-2, \infty)$.

You Try $\PageIndex{5}$

Use interval notation to describe the solution of: \[−3x≥− 6 \nonumber \]

Answer: $(-\infty, 2]$

Sometimes you need to perform a sequence of steps to arrive at the solution.

Example $\PageIndex{7}$

Solve for $x: \quad 2 x +5> −7$. Sketch the solution on the real line, then use interval notation to describe your solution.

Solution

To “undo” adding $5$, subtract $5$ from both sides of the inequality.

\[\begin{aligned} 2x+5&> -7 & & \color {Red} \text { Original inequality. } \\ 2x+5-5&> -7-5 & & \color {Red} \text { Subtract } 5 \text { from both sides. } \\ 2x&> -12 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

To “undo” multiplying by $2$, divide both sides by $2$. Because we are dividing both sides by a positive number, we do not reverse the inequality sign.

\[\begin{aligned} \dfrac{2x}{2}& >\dfrac{-12}{2} & & \color {Red} \text { Divide both sides by } 2 \\ x&> -6 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Shade the real numbers greater than $−6$.

$Image of number line excluding -6 with arrow shading to the right$

Using interval notation, the solution is $(-6, \infty)$.

You Try $\PageIndex{6}$

Use interval notation to describe the solution of: \[3x-2 ≤4 \nonumber \]

Answer: $(-\infty, 2]$

Example $\PageIndex{8}$

Solve for $x: \quad 3 −5x ≤ 2x + 17$. Sketch the solution on the real line, then use interval notation to describe your solution.

Solution

We need to isolate terms containing $x$ on one side of the inequality. Start by subtracting $2x$ from both sides of the inequality.

\[\begin{aligned} 3-5x &\leq 2x+17 & & \color {Red} \text { Original inequality. } \\ 3-5x-2x &\leq 2x+17-2x & & \color {Red} \text { Subtract } 2x \text { from both sides. } \\ 3-7x &\leq 17 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

We continue to isolate terms containing $x$ on one side of the inequality. Subtract $3$ from both sides.

\[\begin{aligned} 3-7x-3 &\leq 17-3 & & \color {Red} \text { Subtract } 3 \text { from both sides. } \\ -7x &\leq 14 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

To “undo” multiplying by $−7$, divide both sides by $−7$. Because we are dividing both sides by a negative number, we reverse the inequality sign.

\[\begin{aligned} \dfrac{-7x}{-7} &\geq \dfrac{14}{-7} & & \color {Red} \text { Divide both sides by }-7 \\ x &\geq-2 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

$Image of number line including -2 with arrow shading to the right$

Using interval notation, the solution is $[-2, \infty)$.

You Try $\PageIndex{7}$

Use interval notation to describe the solution of: \[4-x>2x +1 \nonumber \]

Answer: $(-\infty, 1)$

	\( x \geq -3 \)
Shade to the right of \(−3\), and put a bracket at \(−3\).	$Example2.1.jpg$
Write in interval notation.	\( [-3, \infty) \)

	\( x \leq -\dfrac{3}{5} \)
Shade to the left of \(−\frac{3}{5}\), and put a bracket at \(−\frac{3}{5}\).	$Example2.2.jpg$
Write in interval notation.	\( \bigg( -\infty, \dfrac{3}{5}\bigg] \)

Search

Text Color

Text Size

Margin Size

Font Type

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

You Try \(\PageIndex{1}\)

You Try \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

Adding or Subtracting the Same Quantity from Both Sides of an Inequality

Example \(\PageIndex{4}\)

You Try \(\PageIndex{3}\)

Multiplying or Dividing by a Positive Number on Both Sides of an Inequality

Example \(\PageIndex{5}\)

You Try \(\PageIndex{4}\)

Multiplying or Dividing by a Negative Number

Example \(\PageIndex{6}\)

You Try \(\PageIndex{5}\)

Example \(\PageIndex{7}\)

You Try \(\PageIndex{6}\)

Example \(\PageIndex{8}\)

You Try \(\PageIndex{7}\)