2.E: Graphing Functions and Inequalities (Exercises)
- Page ID
- 6390
Exercise \(\PageIndex{1}\)
Determine the domain and range and state whether the function is a relation or not.
1. \(\{ ( - 4 , - 1 ) , ( - 5,3 ) , ( 10,3 ) , ( 11,2 ) , ( 15,1 ) \}\)
2. \(\{ ( - 3,0 ) , ( - 2,1 ) , ( 1,3 ) , ( 2,7 ) , ( 2,5 ) \}\)
3.
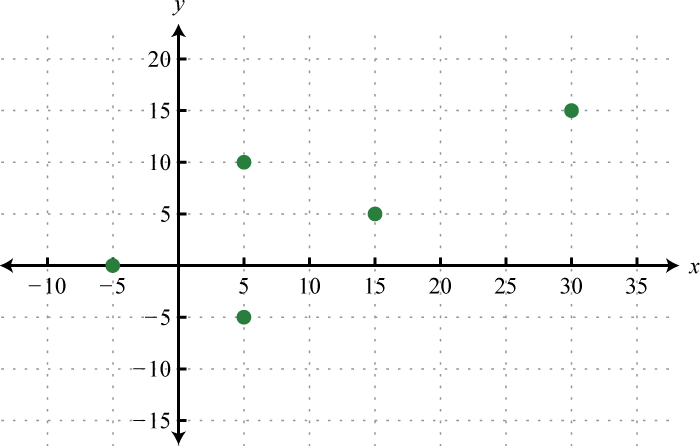
4.

5.
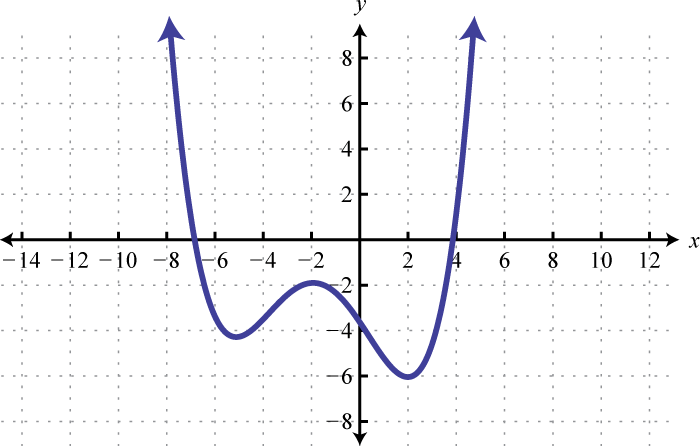
6.
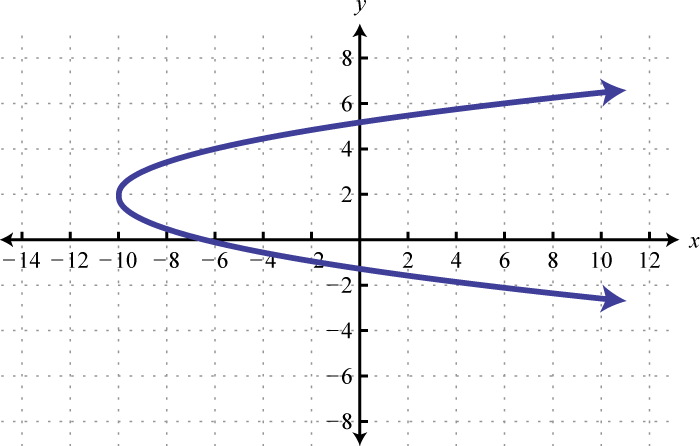
7.
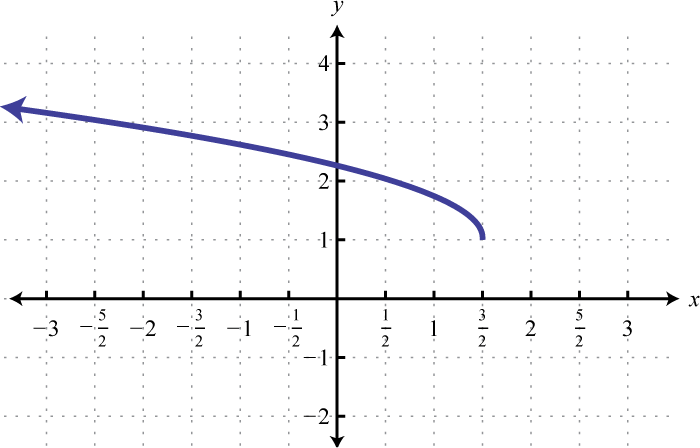
8.
- Answer
-
1. Domain: \(\{ - 5 , - 4,10,11,15 \}\); range: \(\{ - 1,1,2,3 \}\); function: yes
3. Domain: \(\{ - 5,5,15,30 \}\); range: \(\{ - 5,0,5,10,15 \}\); function: no
5. Domain: \(( - \infty , \infty )\); range: \([ - 6 , \infty )\); function: yes
7. Domain: \(\left( - \infty , \frac { 3 } { 2 } \right]\); range: \([ 1 , \infty )\); function yes
Exercise \(\PageIndex{2}\)
Evaluate.
- \(h (x) = 1 2 x − 3; h (−8), h (3),\) and \(h (4a + 1)\)
- \(p (x) = 4 − x ; p (−10), p (0),\) and \(p (5a − 1)\)
- \(f (x) = 2x^{2} − x + 3\); find \(f (−5), f (0)\), and \(f (x + h)\)
- \(g (x) = x^{2} − 9\); find \(f (−3), f (2)\), and \(f (x + h)\)
- \(g (x) = \sqrt{2x − 1}\); find \(g (5), g (1), g (13)\)
- \(h ( x ) = \sqrt [ 3 ] { x + 6 }\); find \(h (−7), h (−6)\), and \(h (21)\)
- \(f (x) = 8x + 3\); find \(x\) where \(f (x) = 10\).
- \(g (x) = 5 − 3x\); find \(x\) where \(g (x) = −4\).
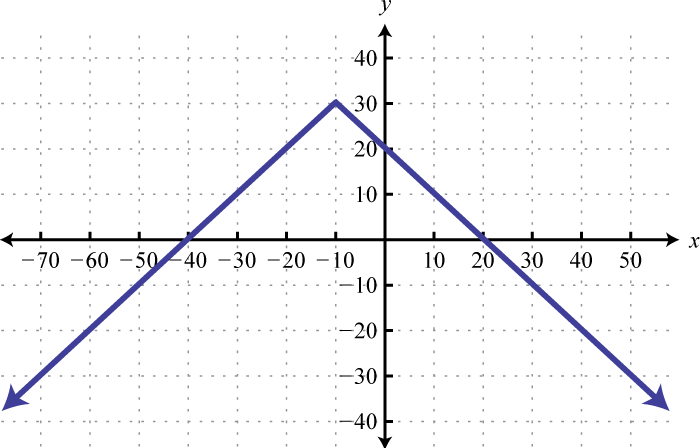
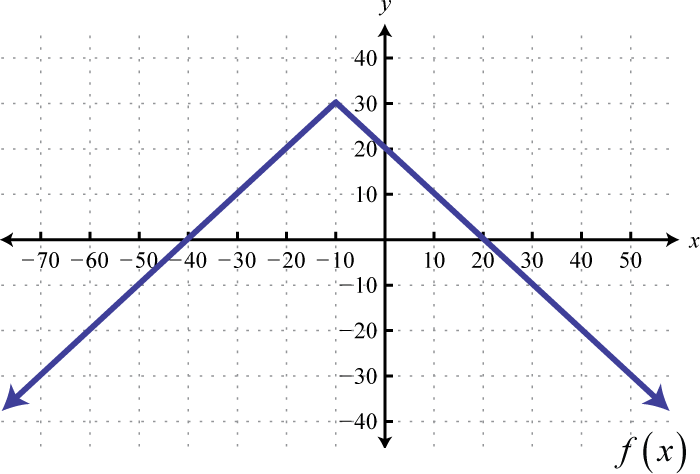
- Given the graph of \(f (x)\) below, find \(f (−60) , f (0)\), and \(f (20)\).
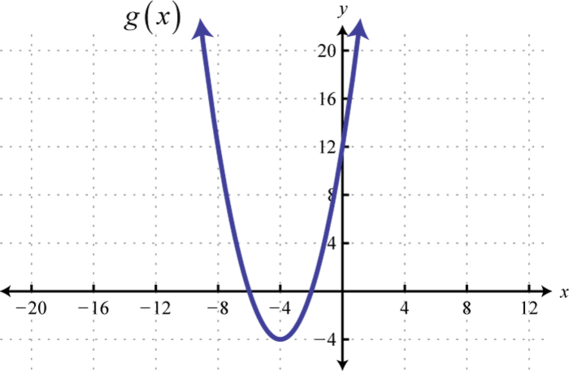
10. . Given the graph of \(g (x)\) below, find \(x\) where \(g (x) = −4\) and \(g (x) = 12\).
- Answer
-
1. \(h (−8) = −7, h (3) = −\frac{3}{2}\), and \(h (4a + 1) = 2a −\frac{5}{2}\)
3. \(f (−5) = 58, f (0) = 3\), and \(f (x + h) = 2x^{2} + 4xh + 2h^{2} − x − h + 3\)
5. \(g (5) = 3, g (1) = 1, g (13) = 5\)
7. \(f \left( \frac { 7 } { 8 } \right) = 10\)
9. \(f ( - 60 ) = - 20 , f ( 0 ) = 20 , f ( 20 ) = 0\)
Exercise \(\PageIndex{3}\)
Graph and label the intercepts.
- \(4x − 8y = 12\)
- \(9x + 4y = 6\)
- \(\frac{3}{8} x + \frac{1}{2} y = \frac{5}{4}\)
- \(\frac{3}{4} x − \frac{1}{2} y = −1\)
- Answer
-
1.
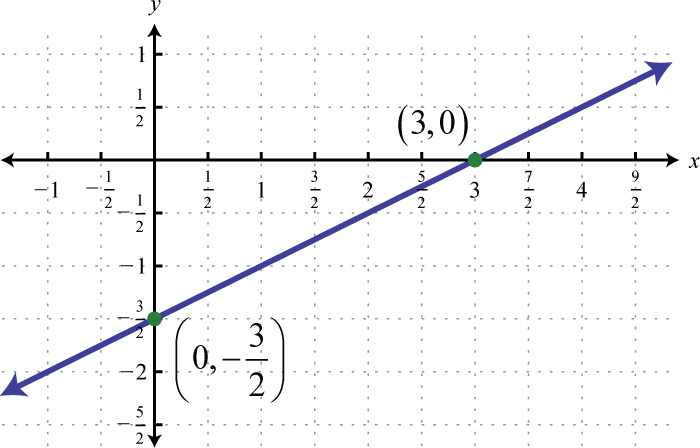
Figure 2.E.9 3.
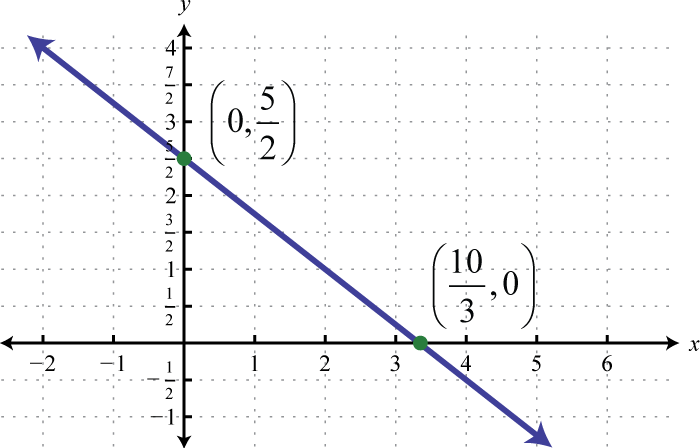
Figure 2.E.10
Exercise \(\PageIndex{4}\)
Graph the linear function and label the \(x\)-intercept.
- \(g ( x ) = \frac { 5 } { 8 } x + 10\)
- \(g ( x ) = - \frac { 1 } { 5 } x - 3\)
- \(f ( x ) = - 4 x + \frac { 1 } { 2 }\)
- \(f ( x ) = 3 x - 5\)
- \(h ( x ) = - \frac { 2 } { 3 } x\)
- \(h ( x ) = - 6\)
- Answer
-
1.
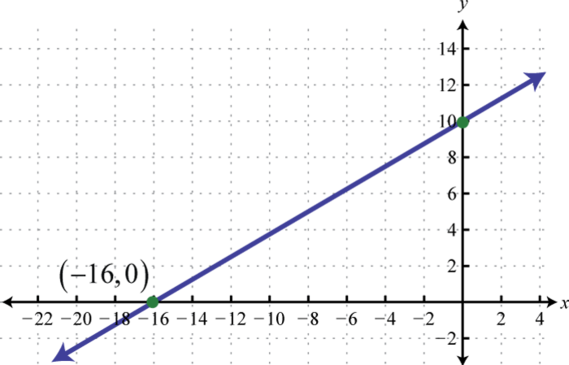
Figure 2.E.11 3.
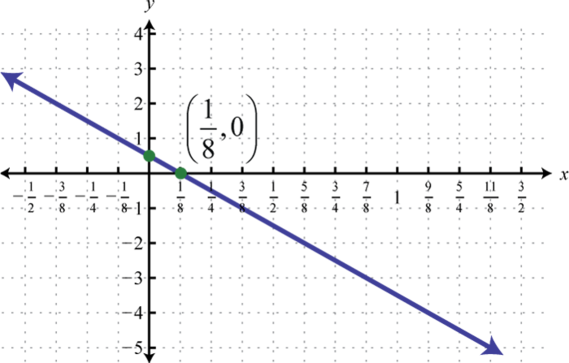
Figure 2.E.12 5.
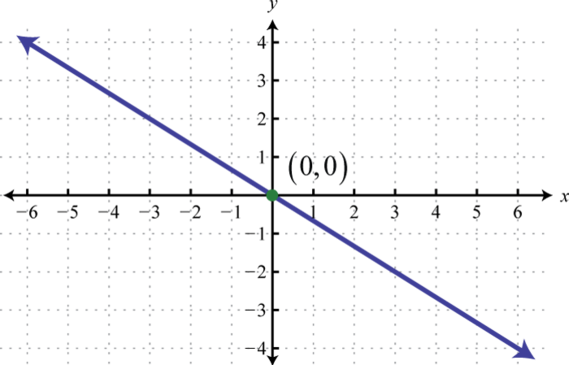
Figure 2.E.13
Exercise \(\PageIndex{5}\)
Find the slope of the line passing through the given points.
- \((−5, 3)\) and \((−4, 1)\)
- \((7, −8)\) and \((−9, −2)\)
- \((−\frac{4}{5}, \frac{1}{3})\) and \((−\frac{1}{10}, −\frac{3}{5})\)
- \((\frac{3}{8}, −1)\) and \((−\frac{3}{4}, −\frac{1}{16})\)
- \((−14, 7)\) and \((−10, 7)\)
- \((6, −5)\) and \((6, −2)\)
- Answer
-
1. \(m=-2\)
3. \(m=-\frac{4}{3}\)
5. \(m=0\)
Exercise \(\PageIndex{6}\)
Graph \(f\) and \(g\) on the same rectangular coordinate plane. Use the graph to find all values of \(x\) for which the given relation is true. Verify your answer algebraically.
- \(f ( x ) = \frac { 1 } { 2 } x - 2 , g ( x ) = - \frac { 5 } { 2 } x + 4 ; f ( x ) = g ( x )\)
- \(f ( x ) = 5 x - 2 , g ( x ) = 3 ; f ( x ) \geq g ( x )\)
- \(f ( x ) = - 4 x + 3 , g ( x ) = - x + 6 ; f ( x ) < g ( x )\)
- \(f ( x ) = \frac { 3 } { 5 } x - 1 , g ( x ) = - \frac { 3 } { 5 } x + 5 ; f ( x ) \leq g ( x )\)
- Answer
-
1. \(x=2\)
3. \(( - 1 , \infty )\)
Exercise \(\PageIndex{7}\)
Find the linear function passing through the given points.
- \((1, −5)\) and \((\frac{1}{2}, −4)\)
- \((\frac{5}{3}, −3)\) and \((−2, 8)\)
- \((7, −6)\) and \((5, −7)\)
- \((−5, −6)\) and \((−3, −9)\)
- Find the equation of the given linear function:
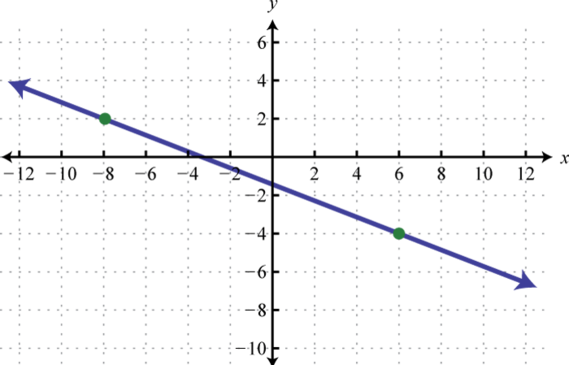
6. Find the equation of the given linear function:
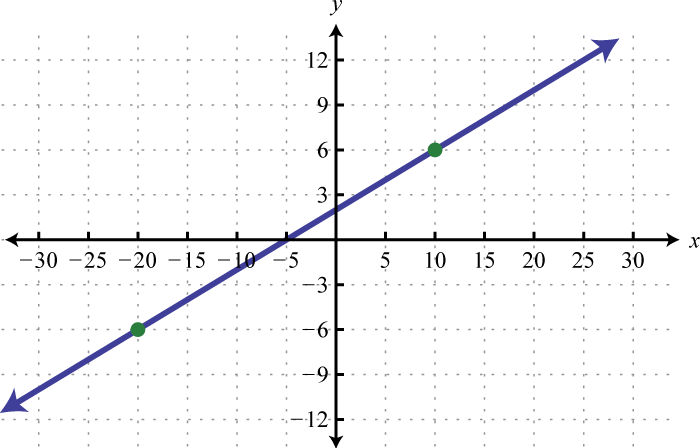
- Answer
-
1. \(f ( x ) = - 2 x - 3\)
3. \(f ( x ) = \frac { 1 } { 2 } x - \frac { 19 } { 2 }\)
5. \(f ( x ) = - \frac { 3 } { 7 } x - \frac { 10 } { 7 }\)
Exercise \(\PageIndex{8}\)
Find the equation of the line:
- Parallel to \(8x − 3y = 24\) and passing through \((−9, 4)\).
- Parallel to \(6x + 2y = 24\) and passing through \((\frac{1}{2}, −2)\).
- Parallel to \(\frac{1}{4} x −\frac{2}{3} y = 1\) and passing through \((−4, −1)\).
- Perpendicular to \(14x + 7y = 10\) and passing through \((8, −3)\).
- Perpendicular to \(15x − 3y = 6\) and passing through \((−3, 1)\).
- Perpendicular to \(\frac { 2 } { 9 } x + \frac { 4 } { 3 } y = \frac { 1 } { 2 }\) and passing through \((2, −7)\).
- Answer
-
1. \(y = \frac{8}{3} x + 28\)
3. \(y = \frac{3}{8} x − \frac{5}{2}\)
5. \(y = −\frac{1}{5} x + \frac{2}{5}\)
Exercise \(\PageIndex{9}\)
Use algebra to solve the following.
- A taxi fare in a certain city includes an initial charge of \($2.50\) plus \($2.00\) per mile driven. Write a function that gives the cost of a taxi ride in terms of the number of miles driven. Use the function to determine the number of miles driven if the total fare is \($9.70\).
- A salesperson earns a base salary of \($1,800\) per month and \(4.2\)% commission on her total sales for that month. Write a function that gives her monthly salary based on her total sales. Use the function to determine the amount of sales for a month in which her salary was \($4,824\).
- A certain automobile sold for \($1,200\) in \(1980\), after which it began to be considered a collector’s item. In \(1994\), the same automobile sold at auction for \($5,750\). Write a linear function that models the value of the automobile in terms of the number of years since \(1980\). Use it to estimate the value of the automobile in the year \(2000\).
- A specialized industrial robot was purchased new for \($62,400\). It has a lifespan of \(12\) years, after which it will be considered worthless. Write a linear function that models the value of the robot. Use the function to determine its value after \(8\) years of operation.
- In \(1950\), the U.S. Census Bureau estimated the population of Detroit, MI to be \(1.8\) million people. In \(1990\), the population was estimated to have decreased to \(1\) million. Write a linear function that gives the population of Detroit in millions of people, in terms of years since \(1950\). Use the function to estimate the year in which the population decreased to \(700,000\) people.
- Online sales of a particular product are related to the number of clicks on its advertisement. It was found that \(100\) clicks in a week result in \($112\) of online sales, and that \(500\) clicks result in \($160\) of online sales. Write a linear function that models the online sales of the product based on the number of clicks on its advertisement. How many clicks are needed to result in \($250\) of weekly online sales from this product?
- The cost in dollars of producing n bicycles is given by the formula \(C (n) = 80n + 3,380\). If each bicycle can be sold for \($132\), write a function that gives the profit generated by producing and selling \(n\) bicycles. Use the formula to determine the number of bicycles that must be produced and sold to profit at least \($10,000\).
- Determine the breakeven point from the previous exercise.
- Answer
-
1. \(C (x) = 2x + 2.5 ; 3.6\) miles
3. \(V (t) = 325t + 1, 200 ; $7,700\)
5. \(p (x) = −0.02x + 1.8 ; 2005\)
7. \(P (n) = 52n − 3, 380 ; 258\) bicycles
Exercise \(\PageIndex{10}\)
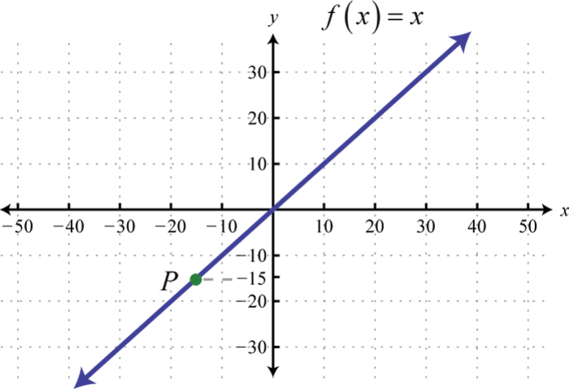
Find the ordered pair that specifies the point \(P\).
1.
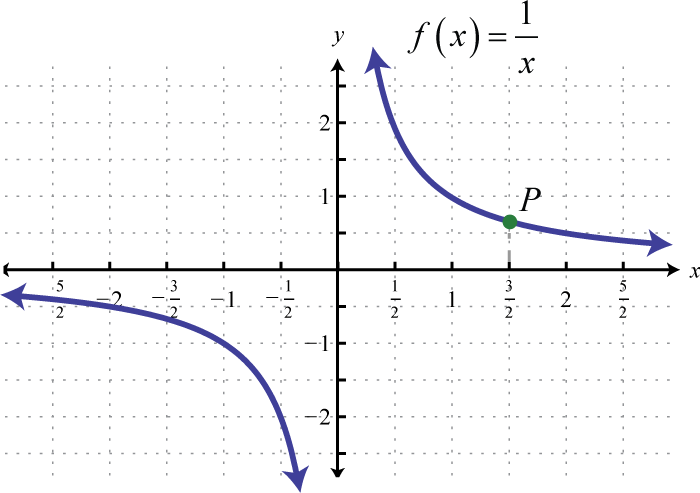
2.
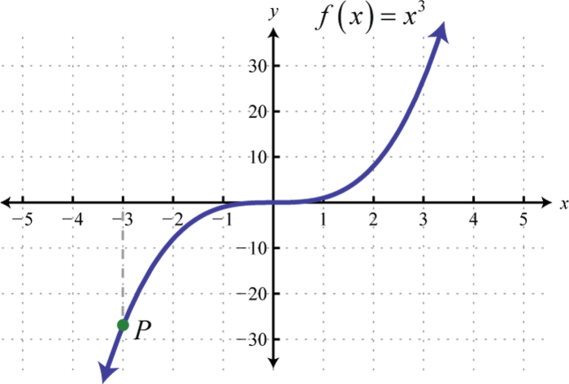
3.
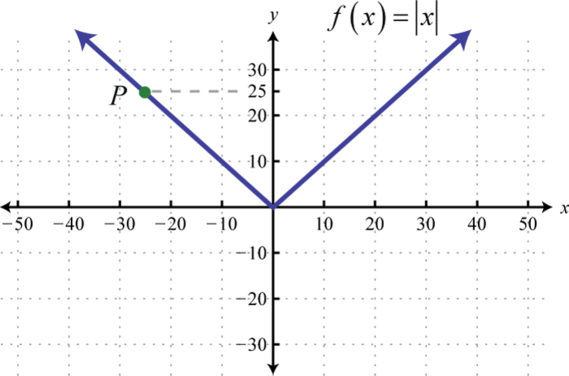
4.
- Answer
-
1. \(\left( \frac { 3 } { 2 } , \frac { 2 } { 3 } \right)\)
3. \(( - 25,25 )\)
Exercise \(\PageIndex{11}\)
Graph the piecewise defined functions.
- \(g ( x ) = \left\{ \begin{array} { l l } { x ^ { 2 } } & { \text { if } x < 5 } \\ { 10 } & { \text { if } x \geq 5 } \end{array} \right.\)
- \(g ( x ) = \left\{ \begin{array} { l l } { - 5 } & { \text { if } x < - 5 } \\ { | x | } & { \text { if } x \geq - 5 } \end{array} \right.\)
- \(f ( x ) = \left\{ \begin{array} { l l } { x } & { \text { if } x \leq - 1 } \\ { x ^ { 3 } } & { \text { if } x > - 1 } \end{array} \right.\)
- \(f ( x ) = \left\{ \begin{array} { l l } { x } & { \text { if } x \leq 4 } \\ { \sqrt { x } } & { \text { if } x > 4 } \end{array} \right.\)
- \(h ( x ) = \left\{ \begin{array} { l l } { x } & { \text { if } x < - 3 } \\ { x ^ { 2 } } & { \text { if } - 3 \leq x < 3 } \\ { - 6 } & { \text { if } x \geq 3 } \end{array} \right.\)
- \(f ( x ) = \left\{ \begin{array} { l l } { 1 } & { \text { if } \quad x < - 1 } \\ { x ^ { 2 } } & { \text { if } } { - 1 \leq x \leq 0 } \\ { \frac { 1 } { x } } & { \text { if } } { x > 0 } \end{array} \right.\)
- \(g ( x ) = \left\{ \begin{array} { c c c } { 1 } & { \text { if } } & { x \leq - 1 } \\ { 0 } & { \text { if } } & { - 1 < x \leq 1 } \\ { - 1 } & { \text { if } } & { x > 1 } \end{array} \right.\)
- \(g ( x ) = \left[\!\![x]\!\!\right] + 2\)
- Answer
-
1.
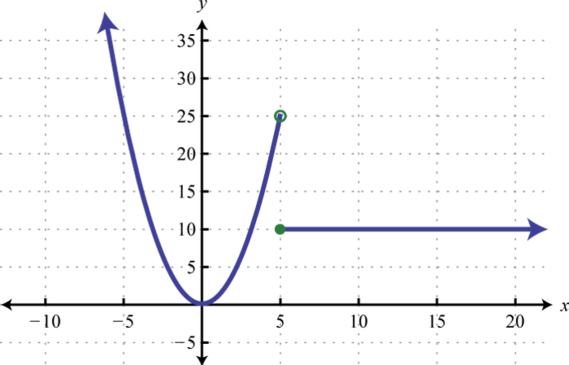
Figure 2.E.20 3.
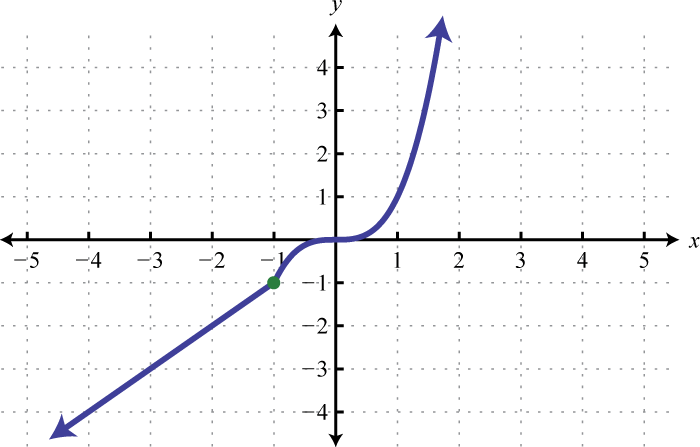
Figure 2.E.21 5.
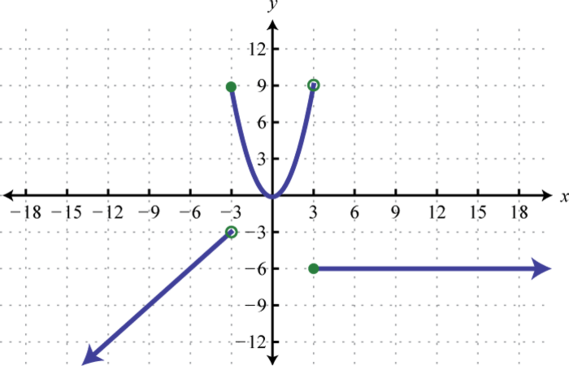
Figure 2.E.22 7.
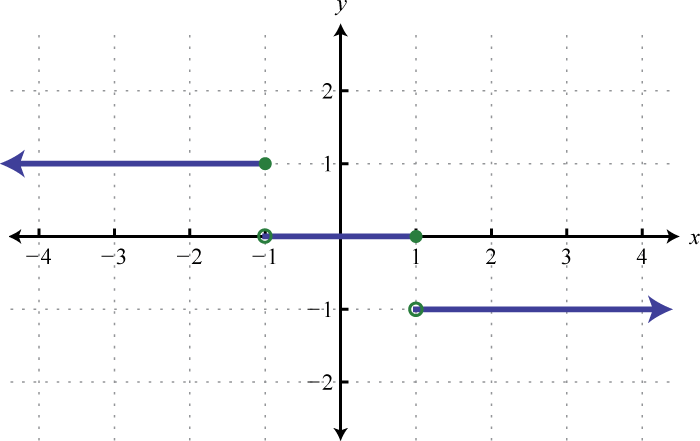
Figure 2.E.23
Exercise \(\PageIndex{12}\)
Evaluate.
1. \(f ( x ) = \left\{ \begin{array} { c l } { 5 x - 2 } & { \text { if } x < - 6 } \\ { x ^ { 2 } } & { \text { if } x \geq - 6 } \end{array} \right.\)
Find \(f (−10), f (−6)\), and \(f (0)\).
2. \(h ( x ) = \left\{ \begin{array} { c l } { 2 - 5 x } & { \text { if } x \leq 0 } \\ { x ^ { 3 } } & { \text { if } x > 0 } \end{array} \right.\)
Find \(h (−1), h (0)\), and \(h (\frac{1}{2})\).
3. \(g ( x ) = \left\{ \begin{array} { c l } { - 5 } & { \text { if } x < - 4 } \\ { x - 9 } & { \text { if } - 4 \leq x < 0 } \\ { \sqrt { x } } & { \text { if } \quad x \geq 0 } \end{array} \right.\)
Find \(g (−10), g (0)\) and \(g (8)\).
4. \(q ( x ) = \left\{ \begin{array} { c c c } { \frac { 1 } { x } } & { \text { if } } & { x < - 1 } \\ { 0 } & { \text { if } } & { - 1 \leq x \leq 1 } \\ { x } & { \text { if } } & { x > 1 } \end{array} \right.\)
Find \(q (− 5 3 ), q (1)\) and \(q (16)\).
- Answer
-
1. \(f ( - 10 ) = - 52 , f ( - 6 ) = 36 , f ( 0 ) = 0\)
3. \(g ( - 10 ) = - 5 , g ( - 4 ) = - 13 , g ( 8 ) = 2 \sqrt { 2 }\)
Exercise \(\PageIndex{13}\)
Sketch the graph of the given function.
- \(f ( x ) = ( x + 5 ) ^ { 2 } - 10\)
- \(g ( x ) = \sqrt { x - 6 } + 9\)
- \(p ( x ) = x - 9\)
- \(h ( x ) = x ^ { 3 } + 5\)
- \(f ( x ) = | x - 20 | - 40\)
- \(f ( x ) = \frac { 1 } { x - 3 }\)
- \(h ( x ) = \frac { 1 } { x + 3 } - 6\)
- \(g ( x ) = \sqrt [ 3 ] { x - 4 } + 2\)
- \(f ( x ) = \left\{ \begin{array} { l l } { ( x + 4 ) ^ { 2 } } & { \text { if } x < - 2 } \\ { x + 2 } & { \text { if } x \geq - 2 } \end{array} \right.\)
- \(g ( x ) = \left\{ \begin{array} { l l } { - 2 } & { \text { if } x < 6 } \\ { | x - 8 | - 4 } & { \text { if } x \geq 6 } \end{array} \right.\)
- \(g ( x ) = - | x + 4 | - 8\)
- \(h ( x ) = - x ^ { 2 } + 16\)
- \(f ( x ) = \sqrt { - x } - 2\)
- \(r ( x ) = - \frac { 1 } { x } + 2\)
- \(g ( x ) = - 2 | x + 10 | + 8\)
- \(f ( x ) = - 5 \sqrt { x + 1 }\)
- \(f ( x ) = - \frac { 1 } { 4 } x ^ { 2 } + 1\)
- \(h ( x ) = \frac { 1 } { 3 } ( x - 1 ) ^ { 3 } + 2\)
- Answer
-
1.
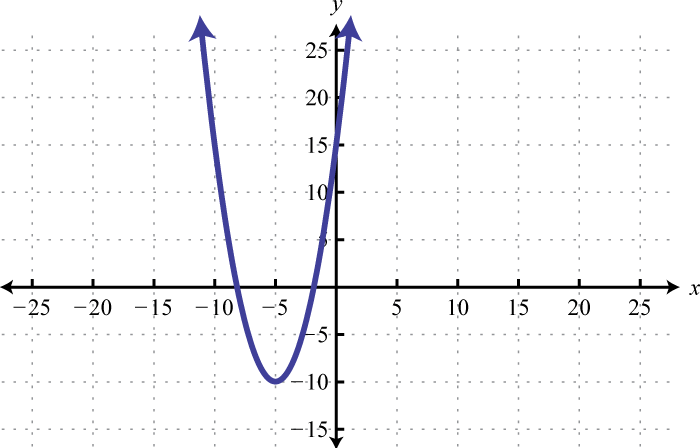
Figure 2.E.24 3.
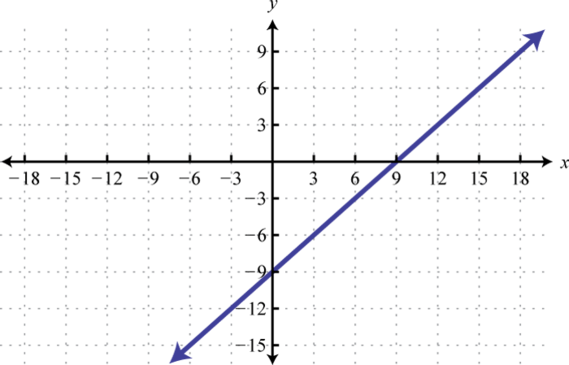
Figure 2.E.25 5.
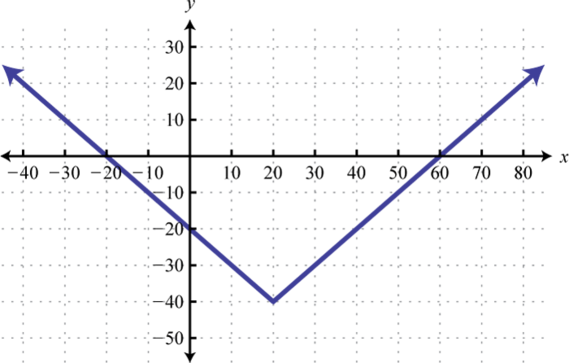
Figure 2.E.26 7.
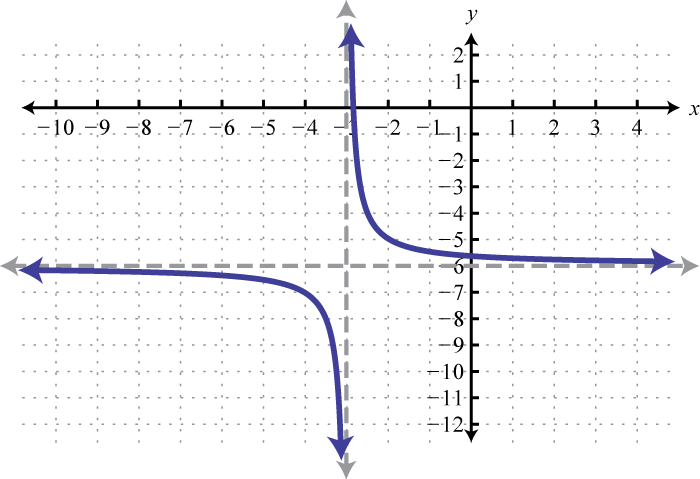
Figure 2.E.27 9.
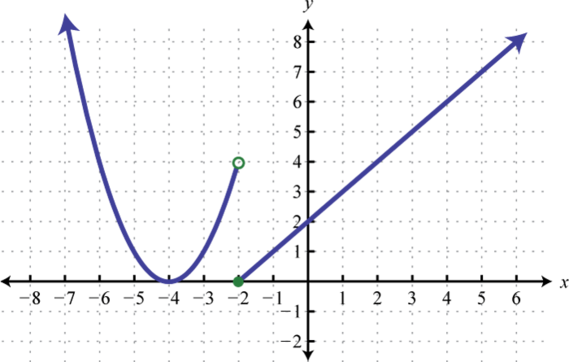
Figure 2.E.28 11.

Figure 2.E.29 13.
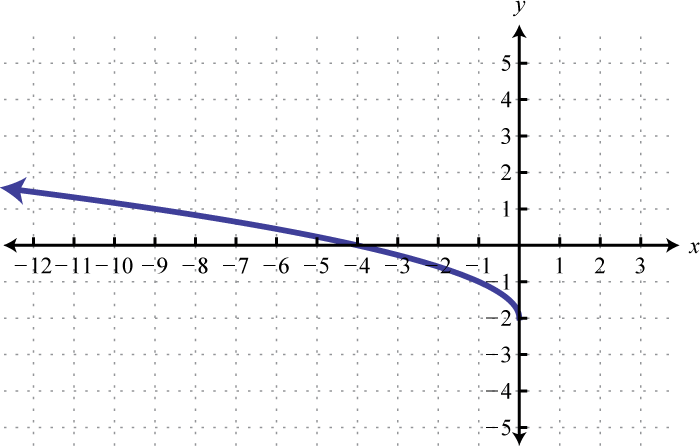
Figure 2.E.30 15.
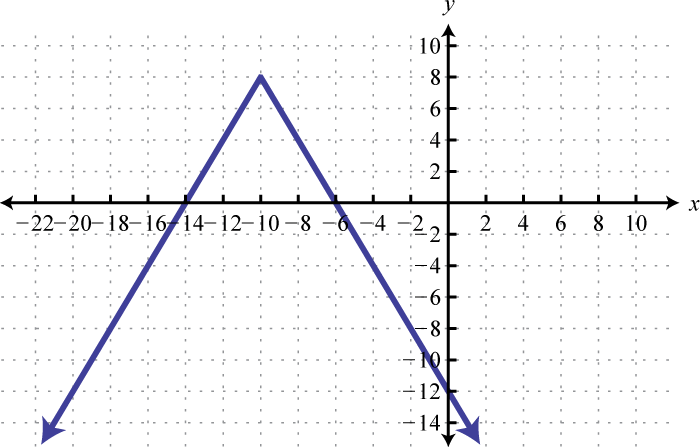
Figure 2.E.31 17.
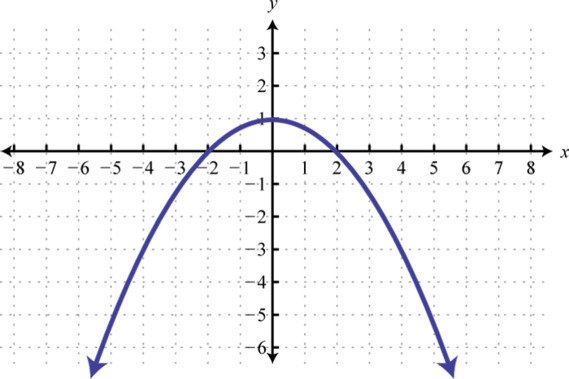
Figure 2.E.32
Exercise \(\PageIndex{14}\)
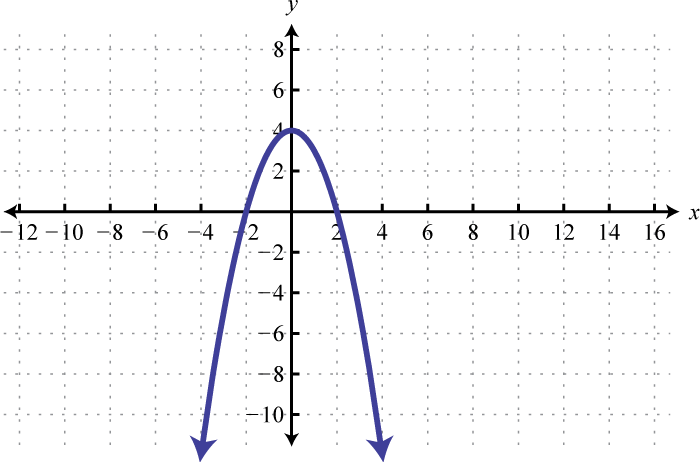
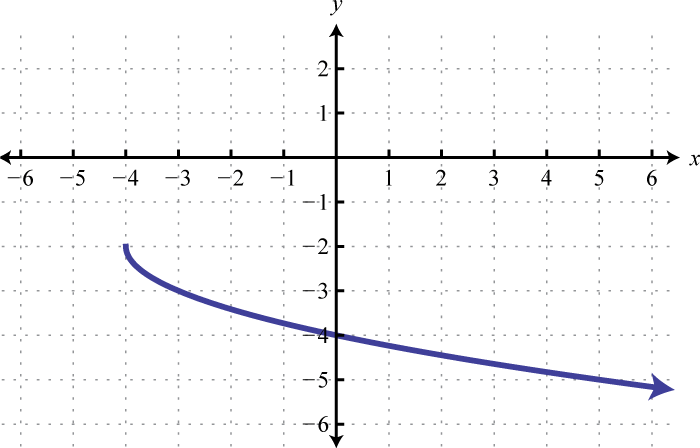
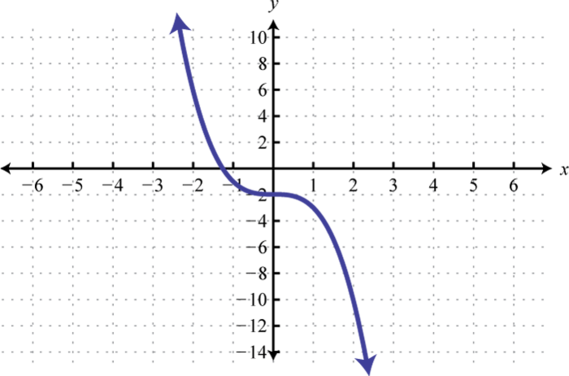
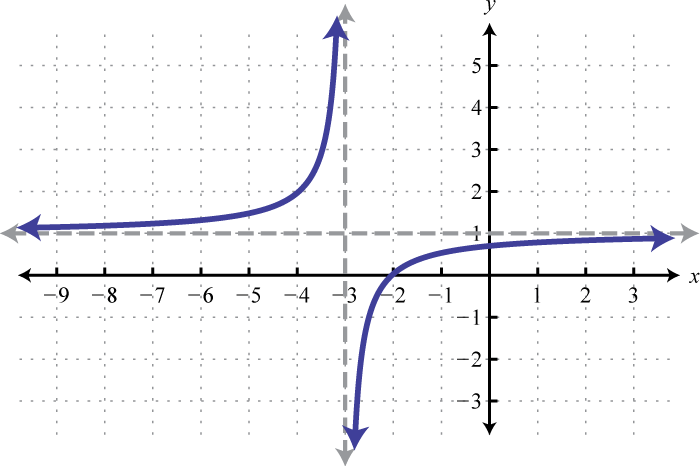
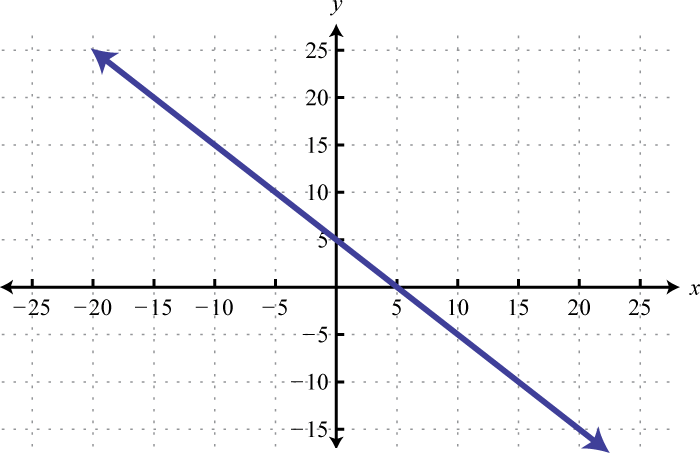
Write an equation that represents the function whose graph is given.
1.
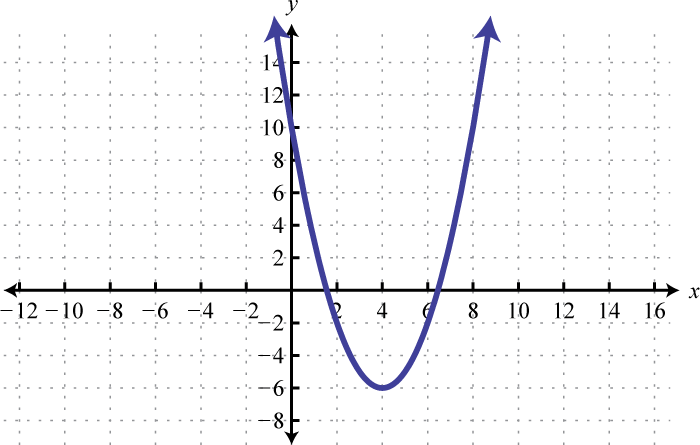
2.
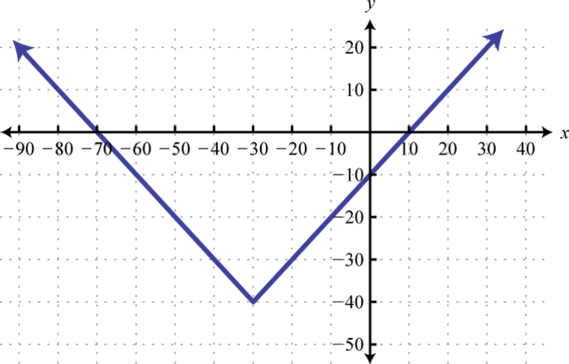
3.
4.
5.
6.
7.

8.
- Answer
-
1. \(f ( x ) = ( x - 4 ) ^ { 2 } - 6\)
3. \(f ( x ) = - x ^ { 2 } + 4\)
5. \(f ( x ) = - x ^ { 3 } - 2\)
7. \(f ( x ) = - 10\)
Exercise \(\PageIndex{15}\)
Solve.
- \(|5x − 4| = 14\)
- \(|4 − 3x| = 4\)
- \(9 − 5 |x − 4| = 4\)
- \(6 + 2 |x + 10| = 12\)
- \(|3x − 6| + 5 = 5\)
- \(0.2 |x − 1.8| = 4.6\)
- \(\frac { 2 } { 3 } \left| 2 x - \frac { 1 } { 2 } \right| + \frac { 1 } { 3 } = 2\)
- \(\frac { 1 } { 4 } \left| x + \frac { 5 } { 2 } \right| - 2 = \frac { 1 } { 8 }\)
- \(| 3 x - 9 | = | 4 x + 3 |\)
- \(| 9 x - 7 | = | 3 + 8 x |\)
- Answer
-
1. \(- 2 , \frac { 18 } { 5 }\)
3. \(3,5\)
5. \(2\)
7. \(- 1 , \frac { 3 } { 2 }\)
9. \(- 12 , \frac { 6 } { 7 }\)
Exercise \(\PageIndex{16}\)
Solve. Graph the solutions on a number line and give the corresponding interval notation.
- \(| 2 x + 3 | < 1\)
- \(| 10 x - 15 | \leq 25\)
- \(| 6 x - 1 | \leq 11\)
- \(| x - 12 | > 7\)
- \(6 - 4 \left| x - \frac { 1 } { 2 } \right| \leq 2\)
- \(5 - | x + 6 | \geq 4\)
- \(| 3 x + 1 | + 7 \leq 4\)
- \(2 | x - 3 | + 6 > 4\)
- \(5 \left| \frac { 1 } { 3 } x - \frac { 1 } { 2 } \right| > \frac { 5 } { 6 }\)
- \(6.4 - 3.2 | x + 1.6 | > 0\)
- Answer
-
1. \(( - 2 , - 1 )\);
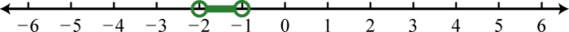
Figure 2.E.41 3. \(\left[ - \frac { 5 } { 3 } , 2 \right]\);

Figure 2.E.42 5. \(\left( - \infty , - \frac { 1 } { 2 } \right] \cup \left[ \frac { 3 } { 2 } , \infty \right)\);

Figure 2.E.43 7. \(\emptyset\);
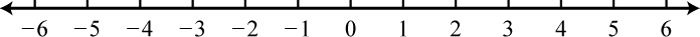
Figure 2.E.44 9. \(( - \infty , 1 ) \cup ( 2 , \infty )\);

Figure 2.E.45
Exercise \(\PageIndex{17}\)
Is the ordered pair a solution to the given inequality?
- \(9 x - 2 y < - 1 ; ( - 1 , - 3 )\);
- \(4 x + \frac { 1 } { 3 } y > 0 ; ( 1 , - 12 )\);
- \(\frac { 3 } { 4 } x - y \geq \frac { 1 } { 2 } ; \left( \frac { 1 } { 2 } , - \frac { 1 } { 4 } \right)\)
- \(x - y \leq - 6 ; ( - 1,7 )\)
- \(y \leq x ^ { 2 } - 3 ; ( - 3,5 )\)
- \(y > | x - 6 | + 10 ; ( - 4,12 )\)
- \(y < ( x - 1 ) ^ { 3 } + 7 ; ( - 1,0 )\)
- \(y \geq \sqrt { x + 4 } ; ( - 3,4 )\)
- Answer
-
1. Yes
3. Yes
5. Yes
7. No
Exercise \(\PageIndex{18}\)
Graph the solution set.
- \(x + y < 6\)
- \(2x − 3y ≥ 9\)
- \(3x − y ≤ 6\)
- \(y + 4 > 0\)
- \(x − 6 ≥ 0\)
- \(−\frac{1}{3} x +\frac{1}{6} y >\frac{1}{2}\)
- \(y > (x − 2)^{2} − 3\)
- \(y ≤ (x + 6)^{2} + 3\)
- \(y < − |x| + 9\)
- \(y > |x − 12| + 3\)
- \(y ≥ x^{3} + 8\)
- \(y > −(x − 2)^{3}\)
- Answer
-
1.
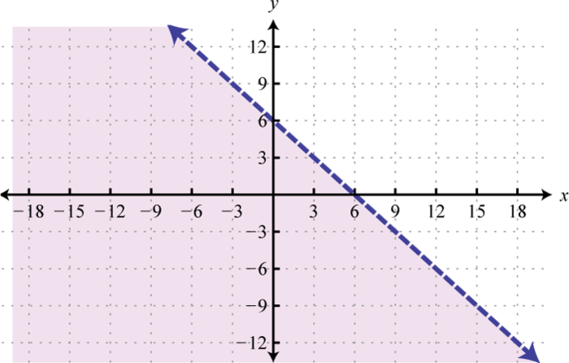
Figure 2.E.46 3.
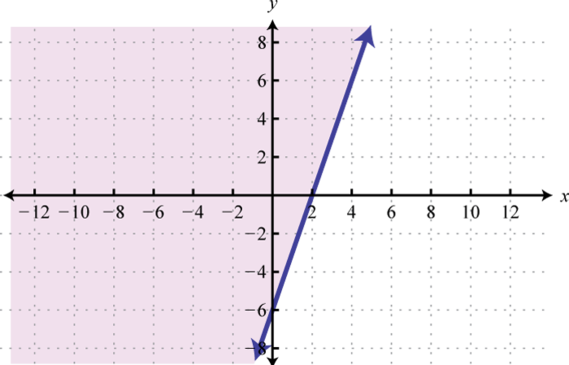
Figure 2.E.47 5.
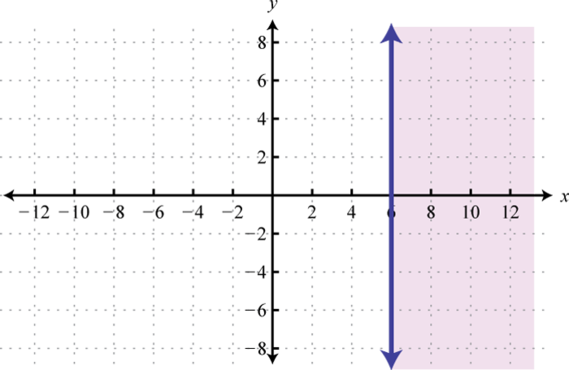
Figure 2.E.48 7.
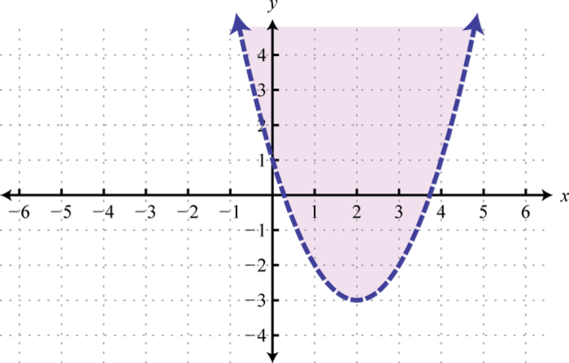
Figure 2.E.49 9.
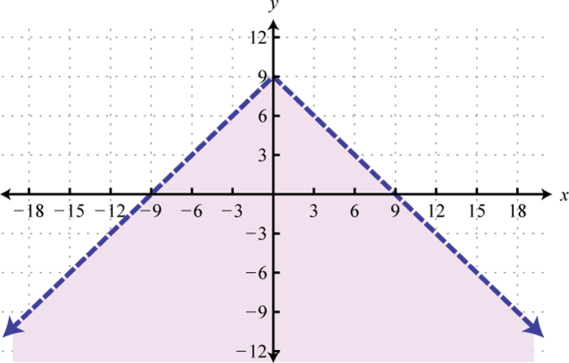
Figure 2.E.50 11.
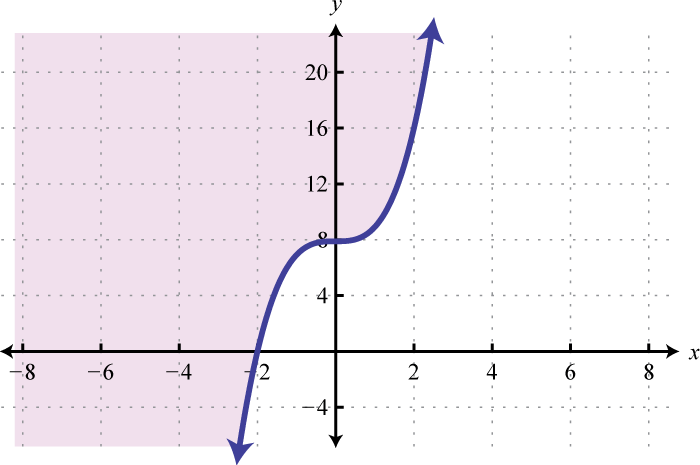
Figure 2.E.51
Sample Exam
Exercise \(\PageIndex{19}\)
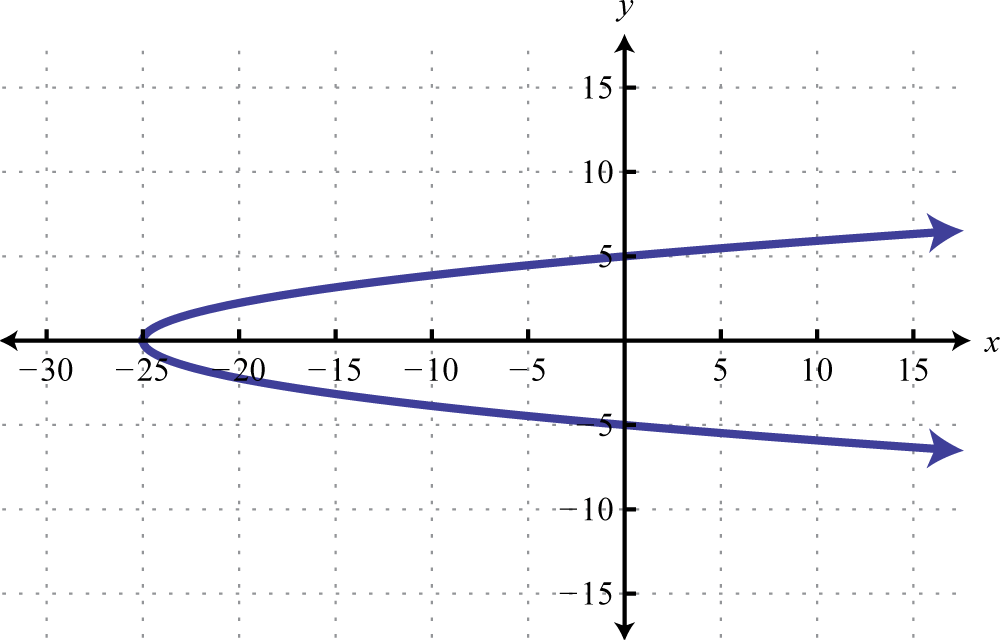
1. Determine whether or not the following graph represents a function or not. Explain.
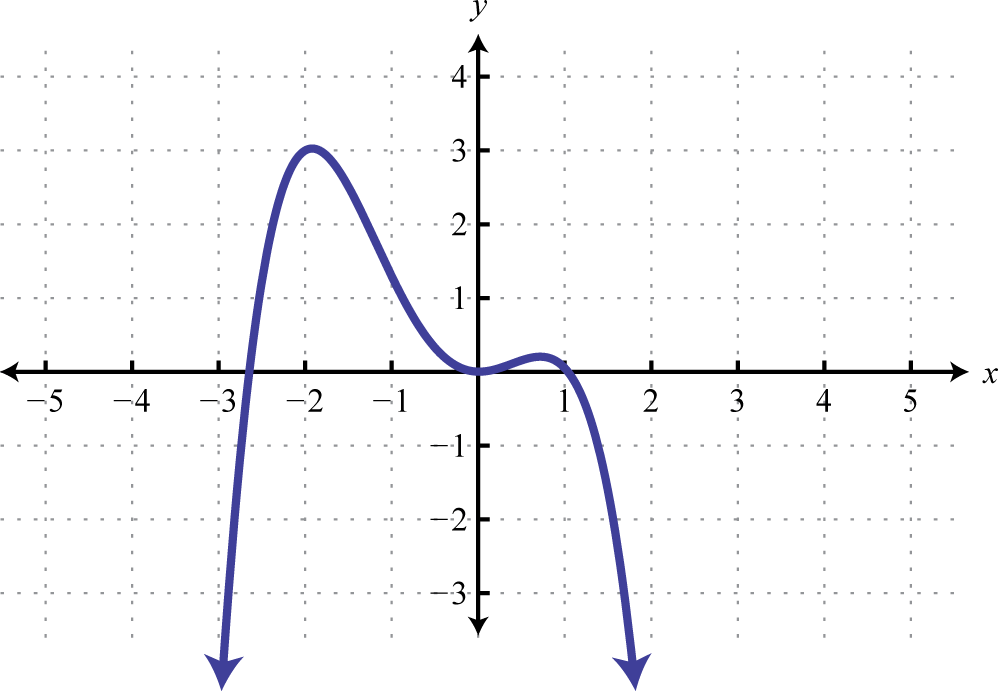
2. Determine the domain and range of the following function.
3. Given \(g (x) = x^{2} − 5x + 1\), find \(g (−1), g (0)\), and \(g (x + h)\).
4. Given the graph of a function \(f\):
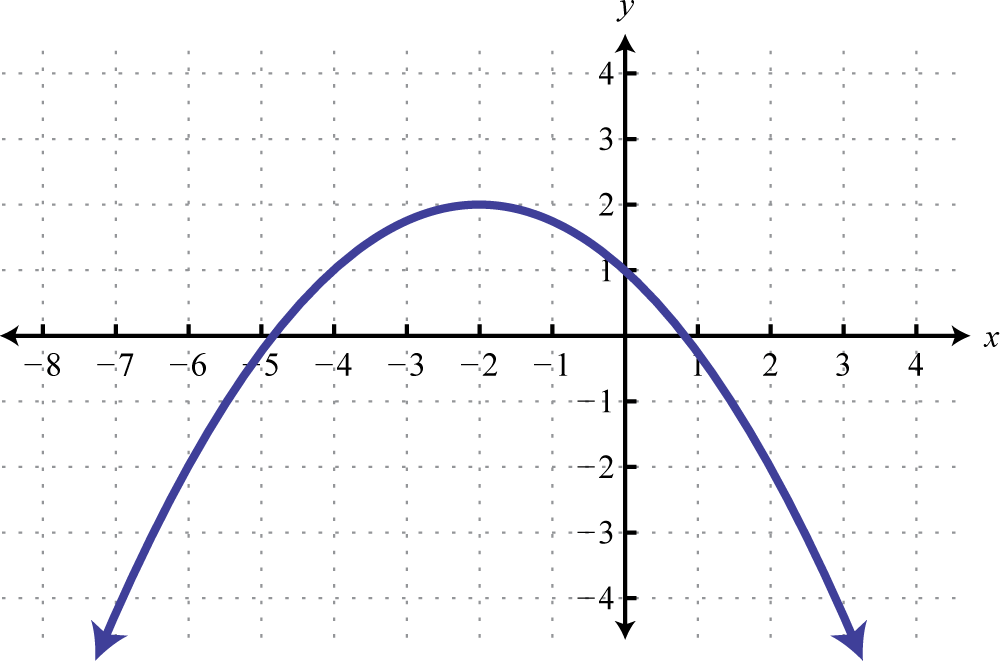
(a) Find \(f(-6), f(0),\) and \(f(2)\)
(b) Find \(x\) where \(f(x)=2\)
5. Graph \(f ( x ) = - \frac { 5 } { 2 } x + 7\) and label the \(x\)-intercept.
6. Find a linear function passing through \((−\frac{1}{2}, −1)\) and \((2, −2)\).
7. Find the equation of the line parallel to \(2x − 6y = 3\) and passing through \((−1, −2)\).
8. Find the equation of the line perpendicular to \(3x − 4y = 12\) and passing through \((6, 1)\).
9. The annual revenue of a new web-services company in dollars is given by \(R (n) = 125n\), where \(n\) represents the number of users the company has registered. The annual maintenance cost of the company’s registered user base in dollars is given by the formula \(C (n) = 85n + 22, 480\) where \(n\) represents the users.
(a) Write a function that models the annual profit based on the number of registered users.
(b) Determine the number of registered users needed to break even.
10. A particular search engine assigns a ranking to a webpage based on the number of links that direct users to the webpage. If no links are found, the webpage is assigned a ranking of \(1\). If \(40\) links are found directing users to the webpage, the search engine assigns a page ranking of \(5\).
(a) Find a linear function that gives the webpage ranking based on the number of links that direct users to it.
(b) How many links will be needed to obtain a page ranking of \(7\)?
- Answer
-
1. The graph is not a function; it fails the vertical line test.
3. \(g (−1) = 7, g (0) = 1\), and \(g (x + h) = x^{2} + 2xh + h^{2} − 5x − 5h + 1\)
5.
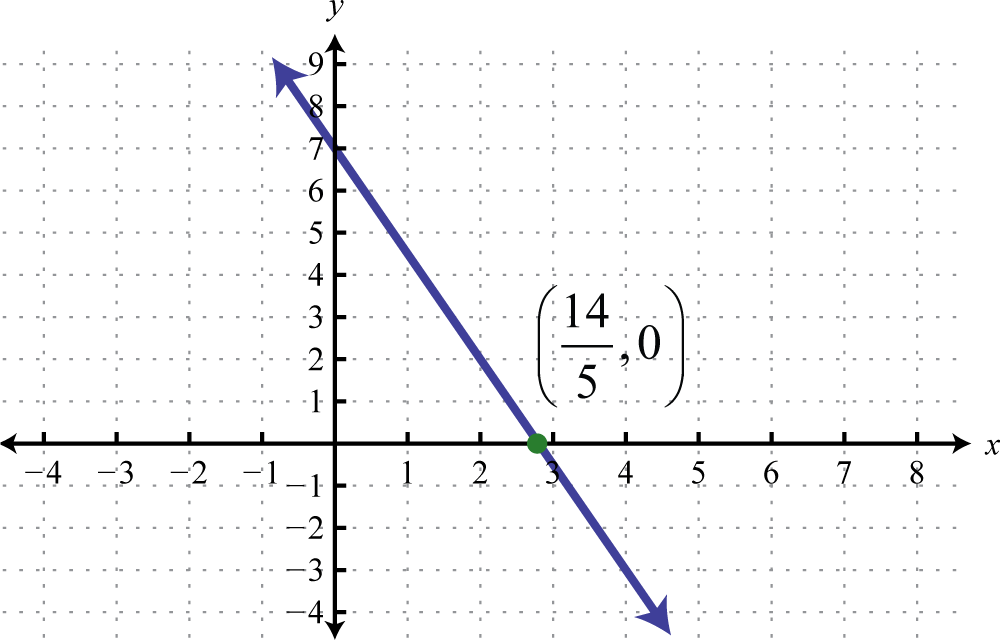
Figure 2.E.55 7. \(y = \frac { 1 } { 3 } x - \frac { 5 } { 3 }\)
9. (a) \(P ( n ) = 40 n - 22,480\) (b) \(562\) users
Exercise \(\PageIndex{20}\)
Use the transformations to sketch the graph of the following functions and state the domain and range.
- \(g ( x ) = | x + 4 | - 5\)
- \(h ( x ) = \sqrt { x - 4 } + 1\)
- \(r ( x ) = - ( x + 3 ) ^ { 3 }\)
- Given the graph, determine the function definition and its domain and range:
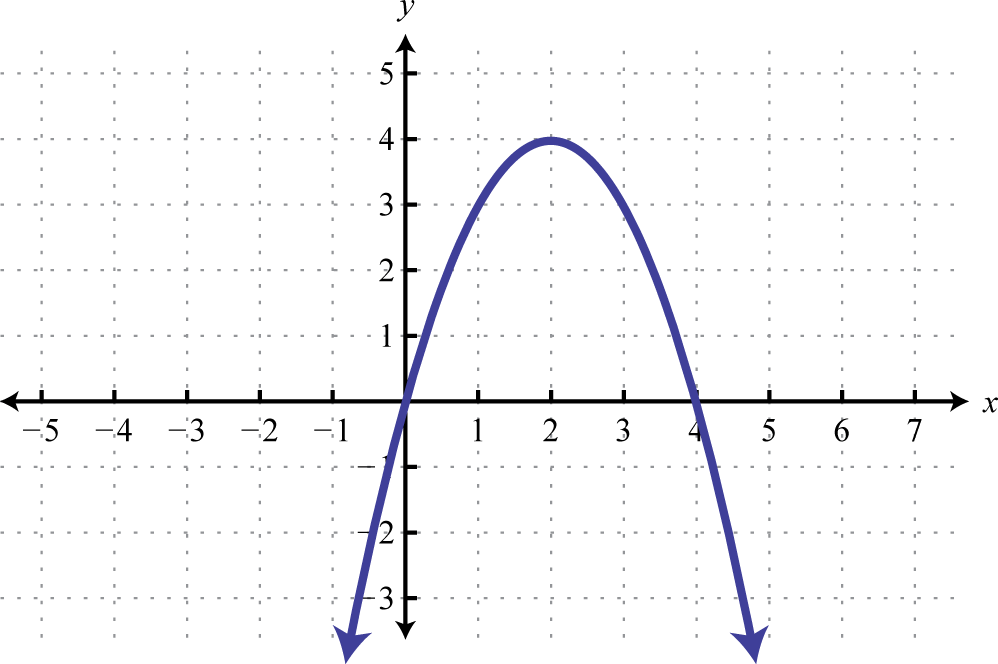
5. Sketch the graph: \(h ( x ) = \left\{ \begin{aligned} - x & \text { if } x < 1 \\ \frac { 1 } { x } & \text { if } x \geq 1 \end{aligned} \right.\)
6. Sketch the graph: \(g ( x ) = - \frac { 1 } { 3 } x ^ { 2 } + 9\)
- Answer
-
1. Domain: \((−∞, ∞)\); range: \([−5, ∞)\)
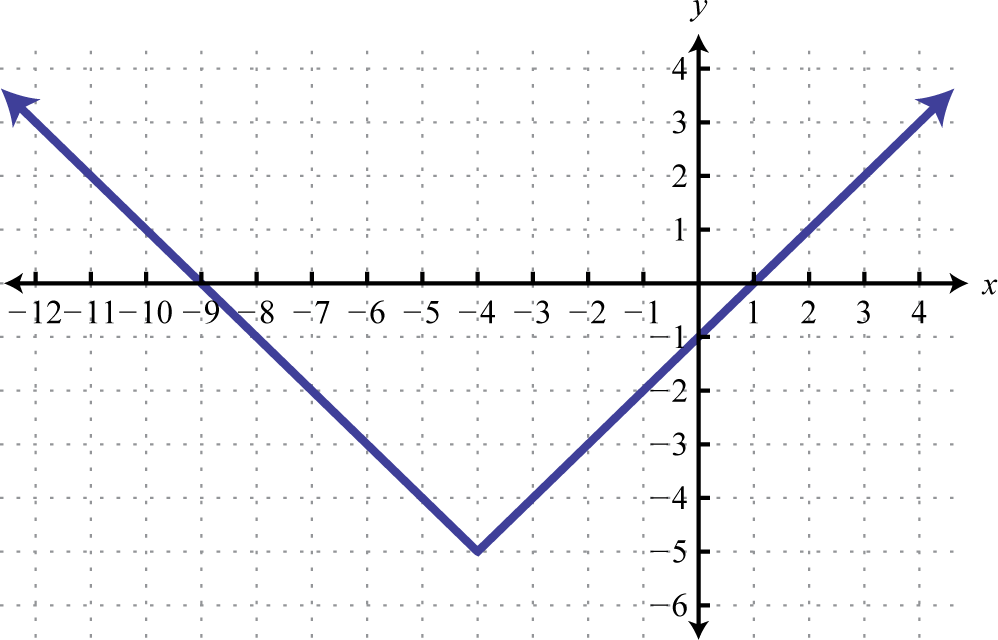
Figure 2.E.57 3. Domain: \((−∞, ∞)\); range: \((−∞, ∞)\)
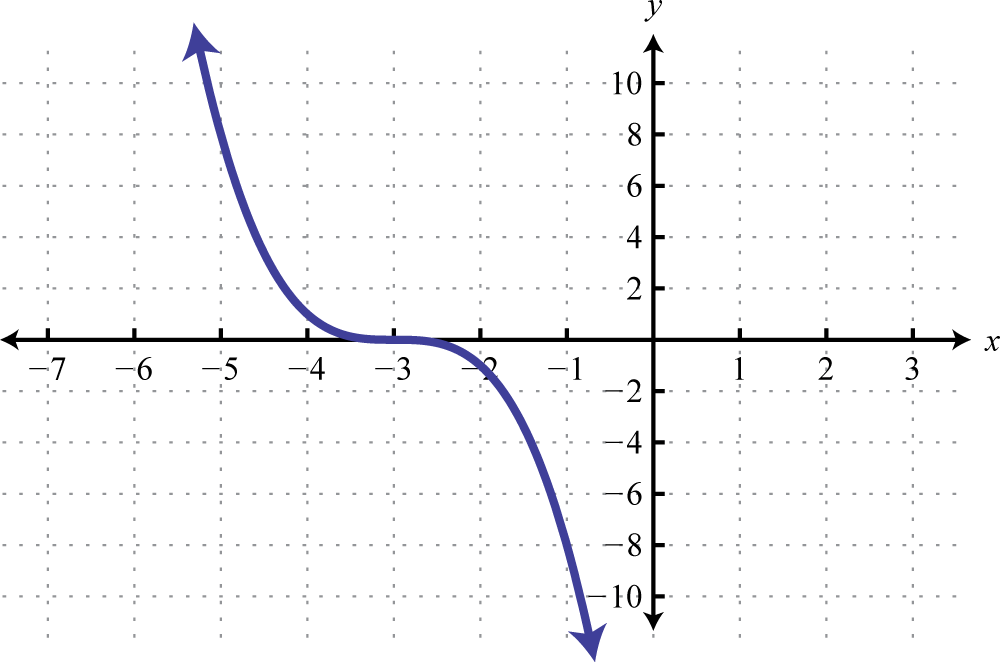
Figure 2.E.58 5.
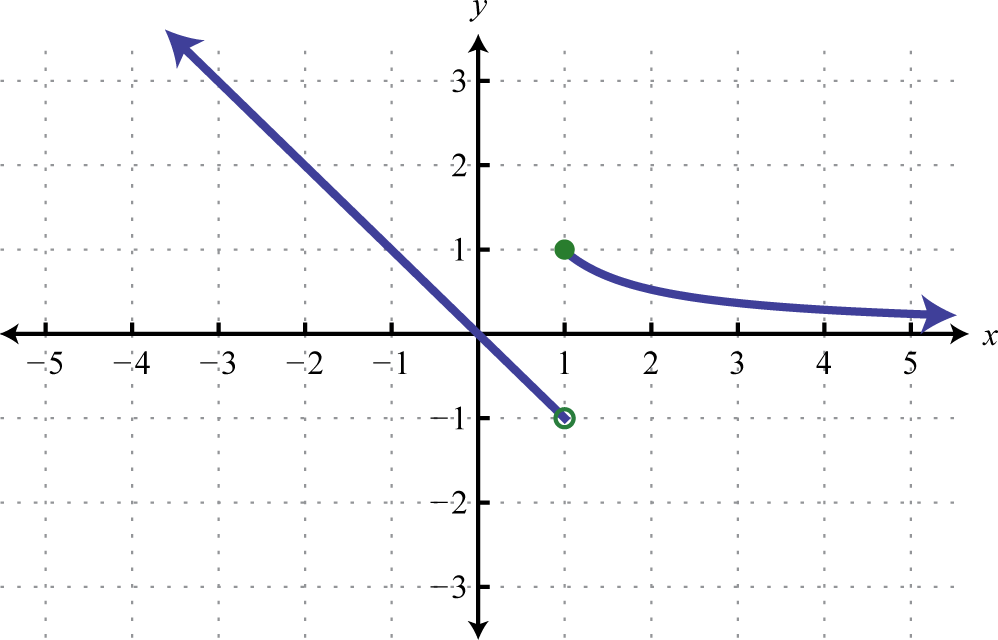
Figure 2.E.59
Exercise \(\PageIndex{21}\)
Solve.
- \(|2 x - 1| + 2 = 7\)
- \(10 - 5 | 2 x - 3 | = 0\)
- \(| 7 x + 4 | = | 9 x - 1 |\)
- Answer
-
1. \(- 2,3\)
3. \(- \frac { 3 } { 16 } , \frac { 5 } { 2 }\)
Exercise \(\PageIndex{22}\)
Solve and graph the solution set.
- \(| 2 x - 4 | - 5 < 7\)
- \(6 + | 3 x - 5 | \geq 13\)
- \(5 - 3 | x - 4 | \geq - 10\)
- \(3 | 7 x - 1 | + 5 \leq 2\)
- Answer
-
1. \(\left( - \infty , - \frac { 2 } { 3 } \right] \cup [ 4 , \infty )\);

Figure 2.E.60 3. \(\emptyset\)
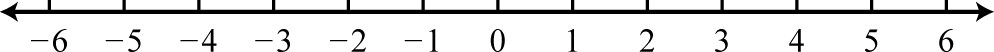
Figure 2.E.61
Exercise \(\PageIndex{23}\)
Graph the solution set.
- \(\frac { 1 } { 2 } x - \frac { 2 } { 3 } y \geq 4\)
- \(y > - ( x - 2 ) ^ { 2 } + 4\)
- Answer
-
1.
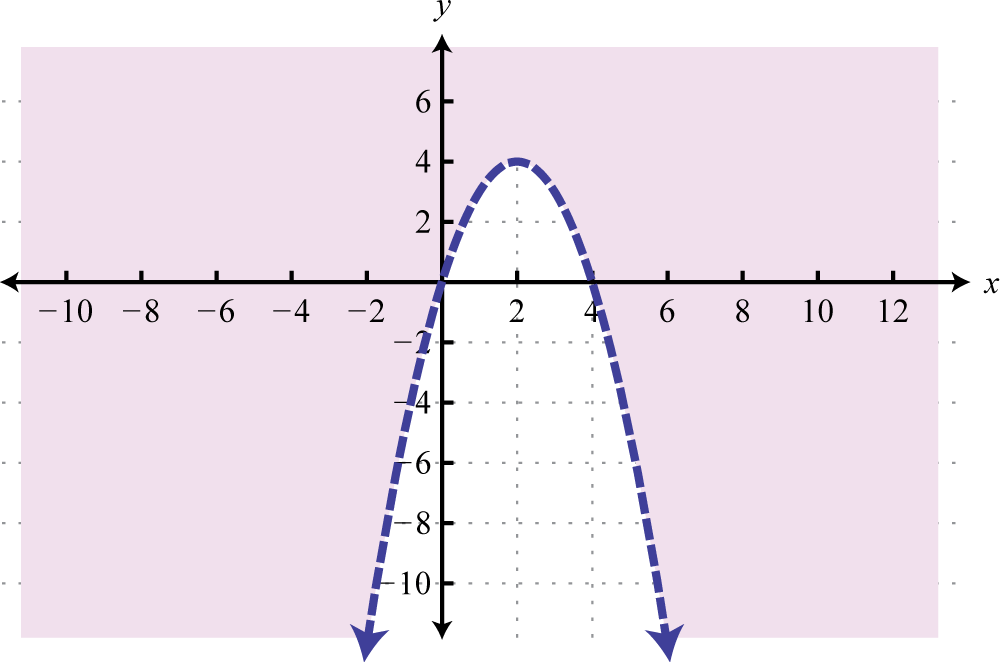
Figure 2.E.62


