1.11: Multiplying Polynomial Expressions

In this chapter, we multiply polynomials. For the multiplication of a monomial by a polynomial, we need to distribute the monomial to multiply each term of the polynomial.

Theorem: Distributive Law

\[a( b + c ) = ab + ac\]

By distributing factors, we can multiply a monomial by a polynomial

Example \(\PageIndex{1}\)

Multiply the terms and simplify.

a) \(3\left(4 x^{2}+5 x\right)=12 x^{2}+15 x\)

b) \(2 p(4 p-7 q)=8 p^{2}-14 p q\)

c) \(-3 a\left(a^{2}-4 a+5\right)=-3 a^{3}+12 a^{2}-15 a\)

d) \(\begin{align*}
6 x+7 y+4(3 x+2 y) &=6 x+7 y+12 x+8 y \\
&=18 x+15 y
\end{align*}\)

e) \(\begin{align*}
2\left(3 x^{2}+5\right)+3 x(4 x-2) &=6 x^{2}+10+12 x^{2}-6 x \\
&=18 x^{2}-6 x+10
\end{align*}\)

f) \(\begin{align*}
y^{2}(y+3)-2 y(-y+5)-4\left(2 y^{2}+12 y+1\right) &=y^{3}+3 y^{2}+2 y^{2}-10 y-8 y^{2}-48 y-4 \\
&=y^{3}-3 y^{2}-58 y-4
\end{align*}\)

g) \(\begin{align*}
-4 a b(-a-3 b)+2 a\left(8 b^{2}-7 a b\right) &=4 a^{2} b+12 a b^{2}+16 a b^{2}-14 a^{2} b \\
&=-10 a^{2} b+28 a b^{2}
\end{align*}\)

When multiplying general polynomials, we need to have a more general distributive law. We show how this is done for the product of two binomials.

Rule \(\PageIndex{2}\): FOIL

To multiply binomials, we need to multiply each term of the first polynomial with each term of the second polynomial. This procedure is known under the name FOIL, which stands for First, Outer, Inner, Last.

For example, when multiplying \((x+3)\) with \((x+5),\) we multiply the terms

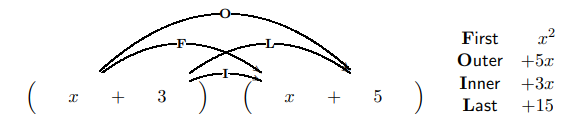
The products of the first terms \(\left(x \cdot x=x^{2}\right),\) the outer terms \((x \cdot 5=5 x),\) the inner terms \((3 \cdot x=3 x),\) and the last terms \((3 \cdot 5=15)\) are added to give the result. Therefore, applying FOIL and combining like terms, we obtain:

\[(x+3)(x+5)=x^{2}+5 x+3 x+15=x^{2}+8 x+15\nonumber\]

Example 9.3

Multiply and simplify.

a) \(\begin{align*}
(x+2)(x-7) &=x^{2}-7 x+2 x-14 \\
&=x^{2}-5 x-14
\end{align*}\)

b) \(\begin{align*}
(2 a+3 b)(4 a+5 b) &=8 a^{2}+10 a b+12 a b+15 b^{2} \\
&=8 a^{2}+22 a b+15 b^{2}
\end{align*}\)

c) \(\begin{align*}
(m-4 n)^{2} &=(m-4 n)(m-4 n) \\
&=m^{2}-4 m n-4 m n+16 n^{2} \\
&=m^{2}-8 m n+16 n^{2}
\end{align*}\)

d) \(\begin{align*}
-5 p(3 p+2 q)^{2} &=-5 p(3 p+2 q)(3 p+2 q) \\
&=-5 p\left(9 p^{2}+6 p q+6 p q+4 q^{2}\right) \\
&=-5 p\left(9 p^{2}+12 p q+4 q^{2}\right) \\
&=-45 p^{3}-60 p^{2} q-20 p q^{2}
\end{align*}\)

Above we have chosen to first evaluate the square \((3 p+2 q)(3 p+2 q) .\) Alternatively, we could also have first multiplied \(-5 p(3 p+2 q),\) which also gives the correct result:

\(\begin{align*}\begin{aligned}
-5 p(3 p+2 q)^{2} &=-5 p(3 p+2 q)(3 p+2 q) \\
&=\left(-15 p^{2}-10 p q\right)(3 p+2 q) \\
&=-45 p^{3}-30 p^{2} q-30 p^{2} q-20 p q^{2} \\
&=-45 p^{3}-60 p^{2} q-20 p q^{2}
\end{aligned}\end{align*}\)

e) \(\begin{align*}
(r+s)^{2}-(r+s)(r-s) &=(r+s)(r+s)-(r+s)(r-s) \\
&=\left(r^{2}+r s+r s+s^{2}\right)-\left(r^{2}-r s+r s-s^{2}\right) \\
&=\left(r^{2}+2 r s+s^{2}\right)-\left(r^{2}-s^{2}\right) \\
&=r^{2}+2 r s+s^{2}-r^{2}+s^{2} \\
&=2 r s+2 s^{2}
\end{align*}\)

f) \(\begin{align*}
2 x y-3(5 x+y)(5 x-y)+4 y(3 x+2 y) &=2 x y-3\left(25 x^{2}-5 x y+5 x y-y^{2}\right)+12 x y+8 y^{2} \\
&=2 x y-3\left(25 x^{2}-y^{2}\right)+12 x y+8 y^{2} \\
&=2 x y-75 x^{2}+3 y^{2}+12 x y+8 y^{2} \\
&=-75 x^{2}+14 x y+11 y^{2}
\end{align*}\)

g) \(\begin{align*}
(2 x-1)\left(x^{2}-4 x+6\right) &=(2 x+(-1))\left(x^{2}-4 x+6\right) \\
&=2 x\left(x^{2}-4 x+6\right)+(-1)\left(x^{2}-4 x+6\right) \\
&=2 x \cdot x^{2}+2 x \cdot(-4 x)+2 x \cdot 6+(-1) \cdot x^{2}+(-1) \cdot(-4 x)+(-1) \cdot 6 \\
&=2 x^{3}-8 x^{2}+12 x-x^{2}+4 x-6 \\
&=2 x^{3}-9 x^{2}+16 x-6
\end{align*}\)

Exit Problem

Multiply: \((5 x-2)\left(x^{2}-3 x-7\right)\)

Simplify: \(-3 a^{3} b^{2}+4 a^{2}\left(a+2 a b^{2}\right)-7 a^{3}\)