2.4: The Pythagorean Theorem

Last updated
Save as PDF

Page ID: 41236

Samar ElHitti, Marianna Bonanome, Holly Carley, Thomas Tradler, & Lin Zhou
CUNY New York City College of Technology & NYC College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The Pythagorean Theorem relates the lengths of the legs of a right triangle and the hypotenuse.

Theorem $\PageIndex{1}$: The Pythagorean Theorem

If $a$ and $b$ are the lengths of the legs of the right triangle and $c$ is the length of the hypotenuse (the side opposite the right angle) as seen in this figure.

$imageedit_2_6209339471.png$

then

\[a^{2}+b^{2}=c^{2}\nonumber\]

Proof

You can verify the truth of the Pythagorean Theorem by measuring various triangles and checking to see that they satisfy $a^{2}+b^{2}=c^{2}$ where $c$ is the length of the hypotenuse and $a$ and $b$ are the lengths of the legs. However, you would have to measure every such triangle to know its absolute truth which, of course, is impossible. We therefore would like to find a way to see it is true for all right triangles. The Pythagorean Theorem can be seen to be true by considering the following construction. Start with the triangle (any right triangle can be oriented this way)

$imageedit_4_7476164357.png$

then construct three other triangles which are the same size and shape as the first (i.e., congruent to the first):

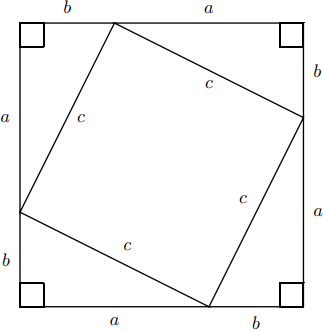
$imageedit_15_3881606840.png$

Now, compute the area of the large square in two ways:

1. Using the area of a square formula:

\[\begin{align*} \text {Area} &=(a+b)^{2} \\[4pt] &=a^{2}+2 a b+b^{2} \end{align*}\]

2. Adding up the sum of the four triangles plus the little square inside:

\[\begin{align*} \text {Area} &=4 \cdot\left(\frac{1}{2} a b\right)+c^{2} \\[4pt] &=2 a b+c^{2} \end{align*}\]

Since both are equal to the area of the square, we must have

\[ a^{2}+2 a b+b^{2}=2 a b+c^{2} \nonumber \]

Subtracting $2 a b$ from both sides gives

\[a^{2}+b^{2}=c^{2}\nonumber\]

$\square$