1.7: Add and Subtract Fractions
- Page ID
- 15122
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Add or subtract fractions with a common denominator
- Add or subtract fractions with different denominators
- Use the order of operations to simplify complex fractions
- Evaluate variable expressions with fractions
A more thorough introduction to the topics covered in this section can be found in the Prealgebrachapter, Fractions.
Add or Subtract Fractions with a Common Denominator
When we multiplied fractions, we just multiplied the numerators and multiplied the denominators right straight across. To add or subtract fractions, they must have a common denominator.
If \(a,b\), and \(c\) are numbers where \(c\neq 0\), then
\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c} \quad \text{and} \quad \dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a - b}{c}\]
To add or subtract fractions, add or subtract the numerators and place the result over the common denominator.
Doing the Manipulative Mathematics activities “Model Fraction Addition” and “Model Fraction Subtraction” will help you develop a better understanding of adding and subtracting fractions.
Find the sum: \(\dfrac{x}{3} + \dfrac{2}{3}\).
Solution
\[\begin{array} {ll} {} &{\dfrac{x}{3} + \dfrac{2}{3}} \\ {\text{Add the numerators and place the sum over the common denominator}} &{\dfrac{x + 2}{3}} \end{array}\]
Find the sum: \(\dfrac{x}{4} + \dfrac{3}{4}\).
- Answer
-
\(\dfrac{x + 3}{4}\)
Find the sum: \(\dfrac{y}{8} + \dfrac{5}{8}\).
- Answer
-
\(\dfrac{y + 5}{8}\)
Find the difference: \(-\dfrac{23}{24} - \dfrac{13}{24}\)
Solution
\[\begin{array} {ll} {} &{-\dfrac{23}{24} - \dfrac{13}{24}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-23 - 13}{24}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Simplify.}} &{\dfrac{-36}{24}} \\ {\text{Simplify. Remember, }-\dfrac{a}{b} = \dfrac{-a}{b}} &{-\dfrac{3}{2}} \end{array}\]
Find the difference: \(-\dfrac{19}{28} - \dfrac{7}{28}\)
- Answer
-
\(-\dfrac{26}{28}\)
Find the difference: \(-\dfrac{27}{32} - \dfrac{1}{32}\)
- Answer
-
\(-\dfrac{7}{8}\)
Find the difference: \(-\dfrac{10}{x} - \dfrac{4}{x}\)
Solution
\[\begin{array} {ll} {} &{-\dfrac{10}{x} - \dfrac{4}{x}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-14}{x}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Rewrite with the sign in front of the fraction.}} &{-\dfrac{14}{x}} \end{array}\]
Find the difference: \(-\dfrac{9}{x} - \dfrac{7}{x}\)
- Answer
-
\(-\dfrac{16}{x}\)
Find the difference: \(-\dfrac{17}{a} - \dfrac{5}{a}\)
- Answer
-
\(-\dfrac{22}{a}\)
Now we will do an example that has both addition and subtraction.
Simplify: \(\dfrac{3}{8} + (-\dfrac{5}{8}) - \dfrac{1}{8}\)
Solution
\[\begin{array} {ll} {\text{Add and Subtract fractions — do they have a }} &{\frac{3}{8} + (-\frac{5}{8}) - \frac{1}{8}} \\ {\text{common denominator? Yes.}} &{} \\ {\text{Add and subtract the numerators and place }} &{\frac{3 + (-5) - 1}{8}} \\ {\text{the result over the common denominator.}} &{} \\ {\text{Simplify left to right.}} &{\frac{-2 - 1}{8}} \\ {\text{Simplify.}} &{-\frac{3}{8}} \end{array}\]
Simplify: \(\dfrac{2}{9} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- Answer
-
\(-1\)
Simplify: \(\dfrac{2}{5} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- Answer
-
\(-\dfrac{2}{3}\)
Add or Subtract Fractions with Different Denominators
As we have seen, to add or subtract fractions, their denominators must be the same. The least common denominator (LCD) of two fractions is the smallest number that can be used as a common denominator of the fractions. The LCD of the two fractions is the least common multiple (LCM) of their denominators.
The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.
Doing the Manipulative Mathematics activity “Finding the Least Common Denominator” will help you develop a better understanding of the LCD.
After we find the least common denominator of two fractions, we convert the fractions to equivalent fractions with the LCD. Putting these steps together allows us to add and subtract fractions because their denominators will be the same!
Add: \(\dfrac{7}{12} + \dfrac{5}{18}\)
Solution



Add: \(\dfrac{7}{12} + \dfrac{11}{15}\)
- Answer
-
\(\dfrac{79}{60}\)
Add: \(\dfrac{13}{15} + \dfrac{17}{20}\)
- Answer
-
\(\dfrac{103}{60}\)
- Do they have a common denominator?
- Yes—go to step 2.
- No—rewrite each fraction with the LCD (least common denominator). Find the LCD. Change each fraction into an equivalent fraction with the LCD as its denominator.
- Add or subtract the fractions.
- Simplify, if possible.
When finding the equivalent fractions needed to create the common denominators, there is a quick way to find the number we need to multiply both the numerator and denominator. This method works if we found the LCD by factoring into primes.
Look at the factors of the LCD and then at each column above those factors. The “missing” factors of each denominator are the numbers we need.

In Exercise \(\PageIndex{13}\), the LCD, 36, has two factors of 2 and two factors of 3.
The numerator 12 has two factors of 2 but only one of 3—so it is “missing” one 3—we multiply the numerator and denominator by 3.
The numerator 18 is missing one factor of 2—so we multiply the numerator and denominator by 2.
We will apply this method as we subtract the fractions in Exercise \(\PageIndex{16}\).
Subtract: \(\dfrac{7}{15} - \dfrac{19}{24}\)
Solution
Do the fractions have a common denominator? No, so we need to find the LCD.
Find the LCD. 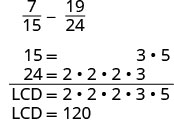 |
|
| Notice, 15 is “missing” three factors of 2 and 24 is “missing” the 5 from the factors of the LCD. So we multiply 8 in the first fraction and 5 in the second fraction to get the LCD. | |
| Rewrite as equivalent fractions with the LCD. |  |
| Simplify. | 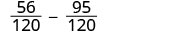 |
| Subtract. | \(-\dfrac{39}{120}\) |
| Check to see if the answer can be simplified. | \(-\dfrac{13\cdot3}{40\cdot3}\) |
| Both 39 and 120 have a factor of 3. | |
| Simplify. | \(-\dfrac{13}{40}\) |
Do not simplify the equivalent fractions! If you do, you’ll get back to the original fractions and lose the common denominator!
Subtract: \(\dfrac{13}{24} - \dfrac{17}{32}\)
- Answer
-
\(\dfrac{1}{96}\)
Subtract: \(\dfrac{7}{15} - \dfrac{19}{24}\)
- Answer
-
\(\dfrac{75}{224}\)
In the next example, one of the fractions has a variable in its numerator. Notice that we do the same steps as when both numerators are numbers.
Add: \(\dfrac{3}{5} + \dfrac{x}{8}\)
Solution
The fractions have different denominators.
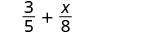 |
|
Find the LCD. 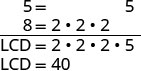 |
|
| Rewrite as equivalent fractions with the LCD. | 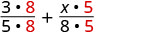 |
| Simplify. | 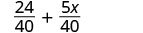 |
| Add. | 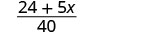 |
Remember, we can only add like terms: \(24\) and \(5x\) are not like terms.
Add: \(\dfrac{y}{6} + \dfrac{7}{9}\)
- Answer
-
\(\dfrac{3y + 14}{18}\)
Add: \(\dfrac{x}{6} + \dfrac{7}{15}\)
- Answer
-
\(\dfrac{15x + 42}{153}\)
We now have all four operations for fractions. Table \(\PageIndex{1}\) summarizes fraction operations.
| Fraction Multiplication | Fraction Division |
| \(\dfrac{a}{b}\cdot \dfrac{c}{d} = \dfrac{ac}{bd}\) Multiply the numerators and multiply the denominators |
\(\dfrac{a}{b}\div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\) Multiply the first fraction by the reciprocal of the second. |
| Fraction Addition | Fraction Subtraction |
| \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\) Add the numerators and place the sum over the common denominator. |
\(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a - b}{c}\) Subtract the numerators and place the difference over the common denominator. |
| To multiply or divide fractions, and LCD is NOT needed. To add or subtract fractions, an LCD is needed. | |
Simplify:
- \(\dfrac{5x}{6} - \dfrac{3}{10}\)
- \(\dfrac{5x}{6}\cdot \dfrac{3}{10}\).
Solution
First ask, “What is the operation?” Once we identify the operation that will determine whether we need a common denominator. Remember, we need a common denominator to add or subtract, but not to multiply or divide.
1. What is the operation? The operation is subtraction.
\[\begin{array} {ll} {\text{Do the fractions have a common denominator? No.}} &{\frac{5x}{6} - \frac{3}{10}} \\ {\text{Rewrite each fractions as an equivalent fraction with the LCD.}} &{\frac{5x\cdot 5}{6\cdot 5} - \frac{3\cdot3}{10\cdot3}} \\ {} &{\frac{25x}{30} - \frac{9}{30}} \\{\text{Subtract the numerators and place the difference over the}} &{\frac{25x - 9}{30}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify, if possible. There are no common factors.}} &{} \\ {\text{The fraction is simplified.}} &{} \end{array}\]
2. What is the operation? Multiplication.
\[\begin{array} {ll} {} &{\frac{5x}{6}\cdot \frac{3}{10}} \\ {\text{To multiply fractions, multiply the numerators and multiply}} &{\frac{5x\cdot 3}{6\cdot 10}} \\ {\text{the denominators}} &{} \\{\text{Rewrite, showing common factors.}} &{\frac{\not 5 x\cdot\not3}{2\cdot\not3\cdot2\cdot\not5}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify.}} &{\frac{x}{4}} \end{array}\]
Simplify:
- \(\dfrac{3a}{4} - \dfrac{8}{9}\)
- \(\dfrac{3a}{4}\cdot\dfrac{8}{9}\)
- Answer
-
- \(\dfrac{27a - 32}{36}\)
- \(\dfrac{2a}{3}\)
Simplify:
- \(\dfrac{4k}{5} - \dfrac{1}{6}\)
- \(\dfrac{4k}{5}\cdot\dfrac{1}{6}\)
- Answer
-
- \(\dfrac{24k - 5}{30}\)
- \(\dfrac{2k}{15}\)
Use the Order of Operations to Simplify Complex Fractions
We have seen that a complex fraction is a fraction in which the numerat or or denominator contains a fraction. The fraction bar indicates division. We simplified the complex fraction \(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) by dividing \(\dfrac{3}{4}\) by \(\dfrac{5}{8}\).
Now we’ll look at complex fractions where the numerator or denominator contains an expression that can be simplified. So we first must completely simplify the numerator and denominator separately using the order of operations. Then we divide the numerator by the denominator.
Simplify: \(\dfrac{(\frac{1}{2})^{2}}{4 + 3^{2}}\)
Solution



Simplify: \(\dfrac{(\frac{1}{3})^{2}}{2^{3} + 2}\)
- Answer
-
\(\dfrac{1}{90}\)
Simplify: \(\dfrac{1 + 4^{2}}{(\frac{1}{4})^{2}}\)
- Answer
-
\(272\)
- Simplify the numerator.
- Simplify the denominator.
- Divide the numerator by the denominator. Simplify if possible.
Simplify: \(\dfrac{\frac{1}{2} + \frac{2}{3}}{\frac{3}{4} - \frac{1}{6}}\)
Solution
\[\begin{array} {ll} {} &{\frac{(\frac{1}{2} + \frac{2}{3})}{(\frac{3}{4} - \frac{1}{6})}} \\ {\text{Simplify the numerator (LCD = 6) and simplify the denominator (LCD = 12).}} &{\frac{(\frac{3}{6} + \frac{4}{6})}{(\frac{9}{12} - \frac{2}{12})}} \\ {\text{Simplify.}} &{\frac{(\frac{7}{6})}{(\frac{7}{12})}} \\{\text{Divide the numerator by the denominator.}} &{\frac{7}{6}\div\frac{7}{12}} \\ {\text{Simplify.}} &{\frac{7}{6}\cdot\frac{12}{7}} \\ {\text{Divide out common factors.}} &{\frac{7\cdot6\cdot2}{6\cdot7}} \\ {\text{Simplify.}} &{2} \end{array}\]
Simplify: \(\dfrac{\frac{1}{3} + \frac{1}{2}}{\frac{3}{4} - \frac{1}{3}}\)
- Answer
-
\(2\)
Simplify: \(\dfrac{\frac{2}{3} - \frac{1}{2}}{\frac{1}{4} + \frac{1}{3}}\)
- Answer
-
\(\dfrac{2}{7}\)
Evaluate Variable Expressions with Fractions
We have evaluated expressions before, but now we can evaluate expressions with fractions. Remember, to evaluate an expression, we substitute the value of the variable into the expression and then simplify.
Evaluate \(x + \dfrac{1}{3}\) when
- \(x = -\dfrac{1}{3}\)
- \(x = -\dfrac{3}{4}\)
Solution
1. To evaluate \(x + \dfrac{1}{3}\) when \(x = -\dfrac{1}{3}\), substitute \(-\dfrac{1}{3}\) for \(x\) in the expression.
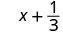 |
|
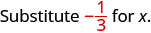 |
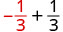 |
| Simplify. | \(0\) |
2. To evaluate \(x + \dfrac{1}{3}\) when \(x = -\dfrac{3}{4}\), substitute \(-\dfrac{3}{4}\) for \(x\) in the expression.
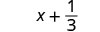 |
|
 |
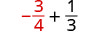 |
| Rewrite as equivalent fractions with the LCD, 12. | 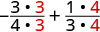 |
| Simplify. | 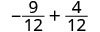 |
| Add. | \(-\dfrac{5}{12}\) |
Evaluate \(x + \dfrac{3}{4}\) when
- \(x = -\dfrac{7}{4}\)
- \(x = -\dfrac{5}{4}\)
- Answer
-
- \(-1\)
- \(-\dfrac{1}{2}\)
Evaluate \(y + \dfrac{1}{2}\) when
- \(y = \dfrac{2}{3}\)
- \(y = -\dfrac{3}{4}\)
- Answer
-
- \(\dfrac{7}{6}\)
- \(-\dfrac{1}{12}\)
Evaluate \(-\dfrac{5}{6} - y\) when \(y = -\dfrac{2}{3}\)
Solution
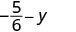 |
|
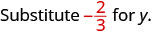 |
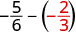 |
| Rewrite as equivalent fractions with the LCD, \(6\). | 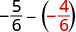 |
| Subtract. | 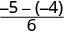 |
| Simplify. | \(-\dfrac{1}{6}\) |
Evaluate \(y + \dfrac{1}{2}\) when \(y = \dfrac{2}{3}\)
- Answer
-
\(-\dfrac{1}{4}\)
Evaluate \(y + \dfrac{1}{2}\) when \(y = \dfrac{2}{3}\)
- Answer
-
\(-\dfrac{17}{8}\)
Evaluate \(2x^{2}y\) when \(x = \dfrac{1}{4}\) and \(y = -\dfrac{2}{3}\).
Solution
Substitute the values into the expression.
| \(2x^{2}y\) | |
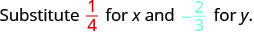 |
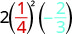 |
| Simplify exponents first. | \(2(\frac{1}{16})(-\frac{2}{3})\) |
| Multiply. Divide out the common factors. Notice we write \(16\) as \(2\cdot2\cdot4\) to make it easy to remove | \(-\frac{\not2\cdot1\cdot\not2}{\not2\cdot\not2\cdot4\cdot3}\) |
| Simplify. | \(-\frac{1}{12}\) |
Evaluate \(3ab^{2}\) when \(a = -\dfrac{2}{3}\) and \(b = -\dfrac{1}{2}\).
- Answer
-
\(-\dfrac{1}{2}\)
Evaluate \(4c^{3}d\) when \(c = -\dfrac{1}{2}\) and \(d = -\dfrac{4}{3}\).
- Answer
-
\(\dfrac{2}{3}\)
The next example will have only variables, no constants.
Evaluate \(\dfrac{p + q}{r}\) when \(p = -4, q = -2\), and \(r = 8\).
Solution
To evaluate \(\dfrac{p + q}{r}\) when \(p = -4, q = -2\), and \(r = 8\), we substitute the values into the expression.
| \(\dfrac{p + q}{r}\) | |
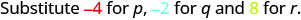 |
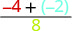 |
| Add in the numerator first. | \(\dfrac{-6}{8}\) |
| Simplify. | \(-\dfrac{3}{4}\) |
Evaluate \(\dfrac{a+b}{c}\) when \(a = -8, b = -7\), and \(c = 6\).
- Answer
-
\(-\dfrac{5}{2}\)
Evaluate \(\dfrac{x+y}{z}\) when \(x = 9, y = -18\), and \(z = -6\).
- Answer
-
\(\dfrac{3}{2}\)
Key Concepts
- Fraction Addition and Subtraction: If \(a, b\), and \(c\) are numbers where \(c\neq 0\), then
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\) and \(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\)
To add or subtract fractions, add or subtract the numerators and place the result over the common denominator. - Strategy for Adding or Subtracting Fractions
- Do they have a common denominator?
Yes—go to step 2.
No—Rewrite each fraction with the LCD (Least Common Denominator). Find the LCD. Change each fraction into an equivalent fraction with the LCD as its denominator. - Add or subtract the fractions.
- Simplify, if possible. To multiply or divide fractions, an LCD IS NOT needed. To add or subtract fractions, an LCD IS needed.
- Do they have a common denominator?
- Simplify Complex Fractions
- Simplify the numerator.
- Simplify the denominator.
- Divide the numerator by the denominator. Simplify if possible.


