1.6E: Exercises
- Page ID
- 30096
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Practice Makes Perfect
Find Equivalent Fractions
In the following exercises, find three fractions equivalent to the given fraction. Show your work, using figures or algebra.
\(\dfrac{3}{8}\)
- Answer
-
\(\dfrac{6}{16}\), \(\dfrac{9}{24}\), \(\dfrac{12}{32}\), answers may vary
\(\dfrac{5}{8}\)
\(\dfrac{5}{9}\)
- Answer
-
\(\dfrac{10}{18}\), \(\dfrac{15}{27}\), \(\dfrac{20}{36}\), answers may vary
\(\dfrac{1}{8}\)
Simplify Fractions
In the following exercises, simplify.
\(-\dfrac{40}{88}\)
- Answer
-
\(-\dfrac{5}{11}\)
\(-\dfrac{63}{99}\)
\(-\dfrac{108}{63}\)
- Answer
-
\(-\dfrac{12}{7}\)
\(-\dfrac{104}{48}\)
\(\dfrac{120}{252}\)
- Answer
-
\(\dfrac{10}{21}\)
\(\dfrac{182}{294}\)
\(-\dfrac{3x}{12y}\)
- Answer
-
\(-\dfrac{x}{4y}\)
\(-\dfrac{4x}{32y}\)
\(\dfrac{14x^{2}}{21y}\)
- Answer
-
\(\dfrac{2x^{2}}{3y}\)
\(\dfrac{24a}{32b^{2}}\)
Multiply Fractions
In the following exercises, multiply.
\(\dfrac{3}{4}\cdot \dfrac{9}{10}\)
- Answer
-
\(\dfrac{27}{40}\)
\(\dfrac{4}{5}\cdot \dfrac{2}{7}\)
\(-\dfrac{2}{3}\cdot -\dfrac{3}{8}\)
- Answer
-
\(\dfrac{1}{4}\)
\(-\dfrac{3}{4}\left(-\dfrac{4}{9}\right)\)
\(-\dfrac{5}{9}\cdot \dfrac{3}{10}\)
- Answer
-
\(-\dfrac{1}{6}\)
\(-\dfrac{3}{8}\cdot \dfrac{4}{15}\)
\(\left(-\dfrac{14}{15}\right)\left(\dfrac{9}{20}\right)\)
- Answer
-
\(-\dfrac{21}{50}\)
\(\left(-\dfrac{9}{10}\right)\left(\dfrac{25}{33}\right)\)
\(\left(-\dfrac{63}{84}\right)\left(-\dfrac{44}{90}\right)\)
- Answer
-
\(\dfrac{11}{30}\)
\(\left(-\dfrac{63}{60}\right)\left(-\dfrac{40}{88}\right)\)
\(4\cdot \dfrac{5}{11}\)
- Answer
-
\(\dfrac{20}{11}\)
\(5\cdot \dfrac{8}{3}\)
\(\dfrac{3}{7}\cdot 21n\)
- Answer
-
9n
\(\dfrac{5}{6}\cdot 30m\)
\(-8\cdot\dfrac{17}{4}\)
- Answer
-
−34
\((-1)\left(-\dfrac{6}{7}\right)\)
Divide Fractions
In the following exercises, divide.
\(\dfrac{3}{4}\div \dfrac{2}{3}\)
- Answer
-
\(\dfrac{9}{8}\)
\(\dfrac{4}{5}\div \dfrac{3}{4}\)
\(-\dfrac{7}{9}\div \left(-\dfrac{7}{4}\right)\)
- Answer
-
\(\dfrac{4}{9}\)
\(-\dfrac{5}{6}\div \left(-\dfrac{5}{6}\right)\)
\(\dfrac{3}{4}\div \dfrac{x}{11}\)
- Answer
-
\(\dfrac{33}{4x}\)
\(\dfrac{2}{5}\div \dfrac{y}{9}\)
\(\dfrac{5}{18}\div -\dfrac{15}{24}\)
- Answer
-
\(-\dfrac{4}{9}\)
\(\dfrac{7}{18}\div \left(-\dfrac{14}{27}\right)\)
\(\dfrac{8u}{15} \div \dfrac{12v}{25}\)
- Answer
-
\(\dfrac{10u}{9v}\)
\(\dfrac{12r}{25}\div \dfrac{18s}{35}\)
\(-5\div \dfrac{1}{2}\)
- Answer
-
-10
\(-3\div \dfrac{1}{4}\)
\(\dfrac{3}{4}\div (-12)\)
- Answer
-
\(\dfrac{1}{16}\)
\(-15\div -\dfrac{5}{3}\)
In the following exercises, simplify.
\(\dfrac{-\dfrac{8}{21}}{\dfrac{12}{35}}\)
- Answer
-
\(-\dfrac{10}{9}\)
\(\dfrac{-\dfrac{9}{16}}{\dfrac{33}{40}}\)
\(\dfrac{-\dfrac{4}{5}}{2}\)
- Answer
-
\(-\dfrac{2}{5}\)
\(\dfrac{5}{\dfrac{3}{10}}\)
\(\dfrac{\dfrac{m}{3}}{\dfrac{n}{2}}\)
- Answer
-
\(\dfrac{2m}{3n}\)
\(\dfrac{-\dfrac{3}{8}}{-\dfrac{y}{12}}\)
Simplify Expressions Written with a Fraction Bar
In the following exercises, simplify.
\(\dfrac{22 + 3}{10}\)
- Answer
-
\(\dfrac{5}{2}\)
\(\dfrac{19 - 4}{6}\)
\(\dfrac{48}{24 - 15}\)
- Answer
-
\(\dfrac{16}{3}\)
\(\dfrac{46}{4 + 4}\)
\(\dfrac{-6 + 6}{8 + 4}\)
- Answer
-
0
\(\dfrac{-6 + 3}{17 - 8}\)
\(\dfrac{4\cdot 3}{6\cdot 6}\)
- Answer
-
\(\dfrac{1}{3}\)
\(\dfrac{6\cdot 6}{9\cdot 2}\)
\(\dfrac{4^{2} - 1}{25}\)
- Answer
-
\(\dfrac{3}{5}\)
\(\dfrac{7^{2} + 1}{60}\)
\(\dfrac{8\cdot 3 + 2\cdot 9}{14 + 3}\)
- Answer
-
\(\dfrac{42}{17}\)
\(\dfrac{9\cdot 6 - 4\cdot 7}{22 + 3}\)
\(\dfrac{5\cdot 6 - 3\cdot 4}{4\cdot 5 -2\cdot 3}\)
- Answer
-
\(\dfrac{9}{7}\)
\(\dfrac{8\cdot 9 - 7\cdot 6}{5\cdot 6 - 9\cdot 2}\)
\(\dfrac{5^{2} - 3^{2}}{3 - 5}\)
- Answer
-
\(-8\)
\(\dfrac{6^{2} - 4^{2}}{4 - 6}\)
\(\dfrac{7\cdot 4 - 2(8 - 5)}{9\cdot 3 - 3\cdot 5}\)
- Answer
-
\(\dfrac{11}{6}\)
\(\dfrac{9\cdot 7 - 3(12- 8)}{8\cdot 7- 6\cdot 6}\)
\(\dfrac{9(8-2)-3(15-7)}{6(7-1) - 3(17-9)}\)
- Answer
-
\(\dfrac{5}{2}\)
\(\dfrac{8(9-2) - 4(14 - 9)}{7(8-3)-3(16 -9)}\)
Translate Phrases to Expressions with Fractions
In the following exercises, translate each English phrase into an algebraic expression.
the quotient of \(r\) and the sum of \(s\) and \(10\)
- Answer
-
\(\dfrac{r}{s + 10}\)
the quotient of \(A\) and the difference of \(3\) and \(B\)
the quotient of the difference of \(x\) and \(y\), and \(−3\)
- Answer
-
\(\dfrac{x - y}{-3}\)
the quotient of the sum of \(m\) and \(n\), and \(4q\)
Everyday Math
Baking. A recipe for chocolate chip cookies calls for \(\frac{3}{4}\) cup brown sugar. Imelda wants to double the recipe.
- How much brown sugar will Imelda need? Show your calculation.
- Measuring cups usually come in sets of \(\frac{1}{4}\), \(\frac{1}{3}\), \(\frac{1}{2}\), and \(1\) cup. Draw a diagram to show two different ways that Imelda could measure the brown sugar needed to double the cookie recipe.
- Answer
-
- \(1\frac{1}{2}\) cups
- answers will vary
Baking. Nina is making 4 pans of fudge to serve after a music recital. For each pan, she needs \(\frac{2}{3}\) cup of condensed milk.
- How much condensed milk will Nina need? Show your calculation.
- Measuring cups usually come in sets of \(\frac{1}{4}\), \(\frac{1}{3}\), \(\frac{1}{2}\), and \(1\) cup. Draw a diagram to show two different ways that Nina could measure the condensed milk needed for \(4\) pans of fudge.
Portions Don purchased a bulk package of candy that weighs \(5\) pounds. He wants to sell the candy in little bags that hold \(\frac{1}{4}\) pound. How many little bags of candy can he fill from the bulk package?
- Answer
-
\(20\) bags
Portions Kristen has \(\frac{3}{4}\) yards of ribbon that she wants to cut into \(6\) equal parts to make hair ribbons for her daughter’s \(6\) dolls. How long will each doll’s hair ribbon be?
Writing Exercises
Rafael wanted to order half a medium pizza at a restaurant. The waiter told him that a medium pizza could be cut into \(6\) or \(8\) slices. Would he prefer \(3\) out of \(6\) slices or \(4\) out of \(8\) slices? Rafael replied that since he wasn’t very hungry, he would prefer \(3\) out of \(6\) slices. Explain what is wrong with Rafael’s reasoning.
- Answer
-
Answers may vary
Give an example from everyday life that demonstrates how \(\dfrac{1}{2}\cdot \dfrac{2}{3}\) is \(\dfrac{1}{3}\).
Explain how you find the reciprocal of a fraction.
- Answer
-
Answers may vary
Explain how you find the reciprocal of a negative number.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
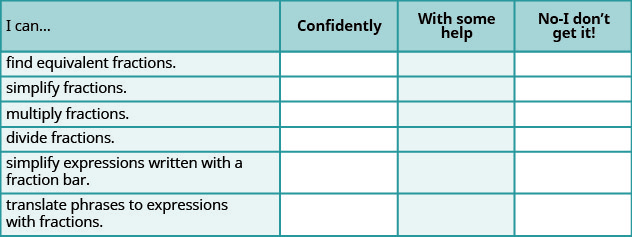
ⓑ After looking at the checklist, do you think you are well prepared for the next section? Why or why not?


