1.3: Use the Language of Algebra
- Page ID
- 15118
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Use variables and algebraic symbols
- Simplify expressions using the order of operations
- Evaluate an expression
- Identify and combine like terms
- Translate an English phrase to an algebraic expression
Use Variables and Algebraic Symbols
Suppose this year Greg is \(20\) years old and Alex is \(23\). You know that Alex is \(3\) years older than Greg. When Greg was \(12\), Alex was \(15\). When Greg is \(35\), Alex will be \(38\). No matter what Greg’s age is, Alex’s age will always be 3 years more, right? In the language of algebra, we say that Greg’s age and Alex’s age are variables and the \(3\) is a constant. The ages change (“vary”) but the \(3\) years between them always stays the same (“constant”). Since Greg’s age and Alex’s age will always differ by \(3\) years, \(3\) is the constant. In algebra, we use letters of the alphabet to represent variables. So if we call Greg’s age \(g\), then we could use \(g + 3g + 3\) to represent Alex’s age. See Table \(\PageIndex{1}\).
| Greg's age | Alex's age |
|---|---|
| \(12\) | \(15\) |
| \(20\) | \(23\) |
| \(35\) | \(38\) |
| \(g\) | \(g+3\) |
The letters used to represent these changing ages are called variables. The letters most commonly used for variables are \(x, y, a, b,\) and \(c\).
A variable is a letter that represents a number whose value may change.
A constant is a number whose value always stays the same.
To write algebraically, we need some operation symbols as well as numbers and variables. There are several types of symbols we will be using.
There are four basic arithmetic operations: addition, subtraction, multiplication, and division. We’ll list the symbols used to indicate these operations below (Table \(\PageIndex{2}\)). You’ll probably recognize some of them. \(\require{enclose}\)
| Operation | Notation | Say: | The result is... |
|---|---|---|---|
| Addition | \(a+b\) | \(a\) plus \(b\) | the sum of \(a\) and \(b\) |
| Subtraction | \(a−b\) | \(a\) minus \(b\) | the difference of \(a\) and \(b\) |
| Multiplication | \(a·b,ab,(a)(b),(a)b,a(b)\) | \(a\) times \(b\) | the product of \(a\) and \(b\) |
| Division | \(a\div{b}, a/b,\dfrac{a}{b}, b \enclose{longdiv}{a}\) | \(a\) divided by \(b\) | the quotient of \(a\) and \(b\), \(a\) is called the dividend, and \(b\) is called the divisor |
We perform these operations on two numbers. When translating from symbolic form to English, or from English to symbolic form, pay attention to the words “of” and “and.”
- The difference of \(9\) and \(2\) means subtract \(9\) and \(2\), in other words, \(9\) minus \(2\), which we write symbolically as \(9−2\).
- The product of \(4\) and \(8\) means multiply \(4\) and \(8\), in other words \(4\) times \(8\), which we write symbolically as \(4\cdot 8\).
In algebra, the cross symbol, \(\times\), is not used to show multiplication because that symbol may cause confusion. Does \(3xy\) mean \(3\times y\) (‘three times \(y\)’) or \(3\cdot x \cdot y\) (three times \(x\) times \(y\))? To make it clear, use \(\cdot\) or parentheses for multiplication.
When two quantities have the same value, we say they are equal and connect them with an equal sign.
\(a = b\) is read “\(a\) is equal to \(b\)”
The symbol \(“=”\) is called the equal sign.
On the number line, the numbers get larger as they go from left to right. The number line can be used to explain the symbols \(“<”\) and \(“>"\).
\(a<b\) is read “\(a\) is less than \(b\)”
\(a\) is to the left of \(b\) on the number line
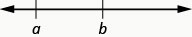
\(a>b\) is read "\(a\) is greater than \(b\)”
\(a\) is to the right of \(b\) on the number line
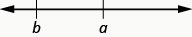
The expressions \(a < b\) or \(a > b\) can be read from left to right or right to left, though in English we usually read from left to right Table \(\PageIndex{3}\). In general, \(a < b\) is equivalent to \(b > a\). For example \(7 < 11\) is equivalent to \(11 > 7\). And \(a > b\) is equivalent to \(b < a\). For example \(17 > 4\) is equivalent to \(4 < 17\).
| Inequality Symbols | Words |
|---|---|
| \(a \neq b\) | \(a\) is not equal to \(b\) |
| \(a < b\) | \(a\) is less than \(b\) |
| \(a \leq b\) | \(a\) is less than or equal to \(b\) |
| \(a > b\) | \(a\) is greater than \(b\) |
| \(a \geq b\) | \(a\) is greater than or not equal to \(b\) |
Translate from algebra into English:
- \(17 \leq 26\)
- \(8 \neq 17 - 3\)
- \(12 > 27 \div 3\)
- \(y + 7 < 19\)
Solution
- \(17 \leq 26\), \(17\) is less than or equal to \(26\)
- \(8 \neq 17 - 3\), \(8\) is not equal to \(17\) minus \(3\)
- \(12 > 27 \div 3\), \(12\) is greater than \(27\) divided by \(3\)
- \(y + 7 < 19\), \(y\) plus \(7\) is less than \(19\)
Translate from algebra into English:
- \(14 \leq 27\)
- \(19 - 2 \neq 8\)
- \(12 > 4 \div 2\)
- \(x - 7 < 1\)
- Answer
-
- \(14\) is less than or equal to \(27\)
- \(19\) minus \(2\) is not equal to \(8\)
- \(12\) is greater than \(4\) divided by \(2\)
- \(x\) minus \(7\) is less than \(1\)
Translate from algebra into English:
- \(19 \leq 15\)
- \(7 = 12 - 5\)
- \(15 \div 3 < 8\)
- \(y + 3 < 6\)
- Answer
-
- \(19\) is greater then or equal to \(15\)
- \(7\) is equal to \(12\) minus \(5\)
- \(15\) divided by \(3\) is less than \(8\)
- \(y\) plus \(3\) is greater than \(6\)
Grouping symbols in algebra are much like the commas, colons, and other punctuation marks in English. They help to make clear which expressions are to be kept together and separate from other expressions. We will introduce three types now.
\[\begin{align*} & \text{Parentheses} & & ( ) \\ & \text{Brackets} & & [ ] \\ & \text{Braces} & & \{ \} \end{align*}\]
Here are some examples of expressions that include grouping symbols. We will simplify expressions like these later in this section.
\[8(14−8) \qquad 21−3[2 + 4(9−8)] \qquad 24\div \{ 13−2[1(6−5)+4] \nonumber\}\]
What is the difference in English between a phrase and a sentence? A phrase expresses a single thought that is incomplete by itself, but a sentence makes a complete statement. “Running very fast” is a phrase, but “The football player was running very fast” is a sentence. A sentence has a subject and a verb. In algebra, we have expressions and equations.
An expression is a number, a variable, or a combination of numbers and variables using operation symbols.
An expression is like an English phrase. Here are some examples of expressions:
| Expression | Words | English Phrase |
|---|---|---|
| \(3 + 5\) | \(3\) plus \(5\) | the sum of three and five |
| \(n − 1\) | \(n\) minus one | the difference of \(n\) and one |
| \(6\cdot 7\) | \(6\) times \(7\) | the product of six and seven |
| \(\dfrac{x}{y}\) | \(x\) divided by \(y\) | the quotient of \(x\) and \(y\) |
Notice that the English phrases do not form a complete sentence because the phrase does not have a verb. An equation is two expressions linked with an equal sign. When you read the words the symbols represent in an equation, you have a complete sentence in English. The equal sign gives the verb.
An equation is two expressions connected by an equal sign.
Here are some examples of equations.
| Equation | English Sentence |
|---|---|
| \(3+5=8\) | the sum of three and five is equal to eight |
| \(n−1=14\) | \(n\) minus one equals fourteen |
| \(6 \cdot 7=42\) | The product of six ans seven is equal to forty-two |
| \(x=53\) | \(x\) is equal to fifty-three |
| \(y+9=2y−3\) | \(y\) plus nine is equal to two \(y\) minus three |
Determine if each is an expression or an equation:
- \(2(x + 3) = 10\)
- \(4(y - 1) + 1\)
- \(x \div 25\)
- \(y + 8 = 40\)
Solution
- \(2(x + 3) = 10\). This is an equation — two expressions are connected with an equal sign.
- \(4(y - 1) + 1\). This is an expression — no equal sign.
- \(x \div 25\). This is an expression — no equal sign.
- \(y + 8 = 40\). This is an equation — two expressions are connected with an equal sign.
Determine if each is an expression or an equation:
- \(3(x - 7) = 27\)
- \(5(4y - 2) - 7\)
- Answer
-
- equation
- expression
Determine if each is an expression or an equation:
- \(y^{3} \div 14\)
- \(4x - 6 = 22\)
- Answer
-
- expression
- equation
Suppose we need to multiply nine factors of \(2\). We could write this as \(2\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\). This is tedious and it can be hard to keep track of all those 2s, so we use exponents. We write \(2\cdot 2 \cdot 2\) as \(2^{3}\) and \(2\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\) as \(2^{9}\). In expressions such as \(2^{3}\), the \(2\) is called the base and the \(3\) is called the exponent. The exponent tells us how many times we need to multiply the base.

We read \(2^{3}\) as “two to the third power” or “two cubed.”
We say \(2^{3}\) is in exponential notation and \(2\cdot 2 \cdot 2\) is in expanded notation.
\(a^{n}\) means the product of \(n\) factors of \(a\).
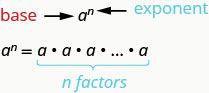
The expression \(a^{n}\) is read \(a\) to the \(n^{th}\) power.
While we read \(a^{n}\) as “\(a\) to the \(n^{th}\) power,” we usually read:
- \(a^{2}\) “a squared”
- \(a^{3}\) “a cubed”
We’ll see later why \(a^{2}\) and \(a^{3}\) have special names.
Table \(\PageIndex{6}\) shows how we read some expressions with exponents.
| Expression | In Words |
|---|---|
| \(7^{2}\) | \(7\) to the second power or \(7\) squared |
| \(5^{3}\) | \(5\) to the third power or \(5\) cubed |
| \(9^{4}\) | \(9\) to the fourth power |
| \(12^{5}\) | \(12\) to the fifth power |
Simplify: \(3^{4}\)
Solution
\[\quad 3^{4}\nonumber\]
\[\begin{align*} & \text{Expand the expression } & & 3 \cdot 3 \cdot 3 \cdot 3 \\[5pt]
& \text{Multiply left to right} & & 9 \cdot 3 \cdot 3 \\[5pt]
& \text{Multiply} & & 27 \cdot 3 \\[5pt]
& \text{Multiply} & & 81 \end{align*}\]
Simplify:
- \(5^{3}\)
- \(1^{7}\)
- Answer
-
- \(125\)
- \(1\)
- \(7^{2}\)
- \(0^{5}\)
- Answer
-
- \(49\)
- \(0\)
Simplify Expressions Using the Order of Operations
To simplify an expression means to do all the math possible. For example, to simplify \(4\cdot 2 + 1\) we’d first multiply \(4\cdot 2\) to get \(8\) and then add the \(1\) to get \(9\). A good habit to develop is to work down the page, writing each step of the process below the previous step. The example just described would look like this:
\[4\cdot 2 + 1\nonumber\]
\[8 + 1\nonumber\]
\[9\nonumber\]
By not using an equal sign when you simplify an expression, you may avoid confusing expressions with equations.
To simplify an expression, do all operations in the expression.
We’ve introduced most of the symbols and notation used in algebra, but now we need to clarify the order of operations. Otherwise, expressions may have different meanings, and they may result in different values. For example, consider the expression:
\[4 + 3\cdot 7\nonumber\]
If you simplify this expression, what do you get?
Some students say \(49\),
\[4 + 3\cdot 7\nonumber\]
Since \(4+3\) gives \(7\).
\[7 \cdot 7\nonumber\]
And \(7\cdot 7\) is \(49\) \[49\nonumber\]
Others say \(25\),
\[4 + 3\cdot 7\nonumber\]
Since \(3\cdot 7\) is \(21\).
\[4 + 21\nonumber\]
And \(21 + 4\) makes \(25\).
\[25\nonumber\]
Imagine the confusion in our banking system if every problem had several different correct answers!
The same expression should give the same result. So mathematicians early on established some guidelines that are called the Order of Operations.
- Parentheses and Other Grouping Symbols
- Simplify all expressions inside the parentheses or other grouping symbols, working on the innermost parentheses first.
- Exponents
- Simplify all expressions with exponents.
- Multiplication and Division
- Perform all multiplication and division in order from left to right. These operations have equal priority.
- Addition and Subtraction
- Perform all addition and subtraction in order from left to right. These operations have equal priority.
Doing the Manipulative Mathematics activity “Game of 24” will give you practice using the order of operations.
Students often ask, “How will I remember the order?” Here is a way to help you remember: Take the first letter of each key word and substitute the silly phrase: “Please Excuse My Dear Aunt Sally.”
\[\begin{align*} &\textbf{P}\text{arentheses} & & \textbf{P}\text{lease} \\[5pt]
&\textbf{E}\text{xponents} & & \textbf{E}\text{xcuse} \\[5pt]
&\textbf{M}\text{ultiplication}\space\textbf{D}\text{ivision} & & \textbf{M}\text{y}\space\textbf{D}\text{ear} \\[5pt]
&\textbf{A}\text{ddition}\space\textbf{S}\text{ubtraction} & & \textbf{A}\text{unt}\space\textbf{S}\text{ally} \end{align*}\]
It’s good that “\(\textbf{M}\text{y}\space\textbf{D}\text{ear}\)” goes together, as this reminds us that multiplication and division have equal priority. We do not always do multiplication before division or always do division before multiplication. We do them in order from left to right.
Similarly, “\(\textbf{A}\text{unt}\space\textbf{S}\text{ally}\)” goes together and so reminds us that addition and subtraction also have equal priority and we do them in order from left to right.
Let’s try an example.
Simplify:
- \(4 + 3\cdot 7\)
- \((4 + 3)\cdot 7\)
Solution
1.| \(4 + 3 \cdot 7\) | |
| Are there any parentheses? No. | |
| Are there any exponents? No. | |
| Is there any multiplication or division? Yes. | |
| Multiply first. | \(4 + {\color{red}{3 \cdot 7}}\) |
| Add. | \(4+21\) |
| \(25\) |
2.
| \((4 + 3)\cdot 7\) | |
| Are there any parentheses? Yes. | \({\color{red}{(4 + 3)}}\cdot 7\) |
| Simplify inside the parentheses. | \(({\color{red}{7}})7\) |
| Are there any exponents? No. | |
| Is there any multiplication or division? Yes. | |
| Multiply. | \(49\) |
Simplify:
- \(12 - 5\cdot 2\)
- \((12 - 5)\cdot 2\)
- Answer
-
- \(2\)
- \(14\)
Simplify:
- \(8 + 3\cdot 9\)
- \((8 + 3)\cdot 9\)
- Answer
-
- \(35\)
- \(99\)
Simplify: \(18\div 6 + 4(5 - 2)\)
Solution
| Parentheses? Yes, subtract first. |
\(18\div 6 + 4(5 - 2)\) |
| Exponents? No. | |
| Multiplication or division? Yes. | \({\color{red}{18\div 6}} + {\color{red}{4(3)}}\) |
| Divide first because we multiply and divide left to right. | \(3+{\color{red}{4(3)}}\) |
| Any other multiplication or division? Yes. | |
| Multiply. | \(3 + 12\) |
| Any other multiplication or division? No. | |
| Any addition or subtraction? Yes. | \(15\) |
Simplify: \(30\div 5 + 10(3 - 2)\)
- Answer
-
\(16\)
Simplify: \(70\div 10 + 4(6 - 2)\)
- Answer
-
\(23\)
When there are multiple grouping symbols, we simplify the innermost parentheses first and work outward.
Simplify: \(5 + 2^{3} + 3[6 - 3(4 - 2)]\).
Solution
| \(5 + 2^{3} + 3[6 - 3(4 - 2)]\) | |
| Are there any parentheses (or other grouping symbol)? Yes. | |
| Focus on the parentheses that are inside the brackets. | \(5 + 2^{3} + 3[6 - 3{\color{red}{(4 - 2)}}]\) |
| Subtract. | \(5 + 2^{3} + 3[6 - {\color{red}{3(2)}}]\) |
| Continue inside the brackets and multiply. | \(5 + 2^{3} + 3[{\color{red}{6 - 6}}]\) |
| Continue inside the brackets and subtract. | \(5 + 2^{3} + 3[{\color{red}{0}}]\) |
| The expression inside the brackets requires no further simplification. | |
| Are there any exponents? Yes. | \(5 + {\color{red}{2^{3}}}+ 3[0]\) |
| Simplify exponents. | \(5 + 8 + {\color{red}{3[0]}}\) |
| Is there any multiplication or division? Yes. | |
| Multiply. | \({\color{red}{5 + 8}}+0\) |
| Is there any addition or subtraction? Yes. | |
| Add. | \({\color{red}{13 + 0}}\) |
| Add. | \(13\) |
Simplify: \(9 + 5^{3} - [4(9 + 3)]\).
- Answer
-
\(86\)
Simplify: \(7^{2} - 2[4(5 + 1)]\).
- Answer
-
\(1\)
Evaluate an Expression
In the last few examples, we simplified expressions using the order of operations. Now we’ll evaluate some expressions—again following the order of operations. To evaluate an expression means to find the value of the expression when the variable is replaced by a given number.
To evaluate an expression means to find the value of the expression when the variable is replaced by a given number.
To evaluate an expression, substitute that number for the variable in the expression and then simplify the expression.
Evaluate \(7x - 4\), when
- \(x = 5\)
- \(x = 1\)
Solution
1.
| when \(x = {\color{red}{5}}\) | \(7x - 4\) |
| \(7({\color{red}{5}}) - 4\) | |
| Multiply. | \(35 - 4\) |
| Subtract. | \(31\) |
2.
| when \(x = {\color{red}{1}}\) | \(7x - 4\) |
| \(7({\color{red}{1}}) - 4\) | |
| Multiply. | \(7 - 4\) |
| Subtract. | \(3\) |
Evaluate \(8x - 3\), when
- \(x = 2\)
- \(x = 1\)
- Answer
-
- \(13\)
- \(5\)
Evaluate \(4y - 4\), when
- \(y = 3\)
- \(y = 5\)
- Answer
-
- \(8\)
- \(16\)
Evaluate \(x = 4\), when
- \(x^{2}\)
- \(3^{x}\)
Solution
1.
| \(x^{2}\) | |
| Replace \(x\) with \({\color{red}{4}}\). | \(({\color{red}{4}})^{2}\) |
| Use definition of exponent. | \(4\cdot 4\) |
| Simplify. | \(16\) |
2.
| \(3^{x}\) | |
| Replace \(x\) with \({\color{red}{4}}\). | \(3^{\color{red}{4}}\) |
| Use definition of exponent. | \(3\cdot3\cdot3\cdot3\) |
| Simplify. | \(81\) |
Evaluate \(x = 3\), when
- \(x^{2}\)
- \(4^{x}\)
- Answer
-
- \(9\)
- \(64\)
Evaluate \(x = 6\), when
- \(x^{3}\)
- \(2^{x}\)
- Answer
-
- \(216\)
- \(64\)
Evaluate \(2x^{2} + 3x + 8\) when \(x = 4\).
Solution
| \(2x^{2} + 3x + 8\) | |
| Substitute \(x = {\color{red}{4}}\). | \(\small{2x^{2} + 3x + 8}\) \(2({\color{red}{4}})^{2} + 3({\color{red}{4}}) + 8\) |
| Follow the order of operations. | \(2(16)+3(4)+8\) |
| \(32+12+8\) | |
| \(52\) |
Evaluate \(3x^{2} + 4x + 1\) when \(x = 3\).
- Answer
-
\(40\)
Evaluate \(6x^{2} - 4x - 7\) when \(x = 2\).
- Answer
-
\(9\)
Identify and Combine Like Terms
Algebraic expressions are made up of terms. A term is a constant, or the product of a constant and one or more variables.
A term is a constant, or the product of a constant and one or more variables.
Examples of terms are \(7, y, 5x^{2}, 9a\), and \(b^{5}\).
The constant that multiplies the variable is called the coefficient.
The coefficient of a term is the constant that multiplies the variable in a term.
Think of the coefficient as the number in front of the variable. The coefficient of the term \(3x\) is \(3\). When we write \(x\), the coefficient is \(1\), since \(x=1\cdot x\).
Identify the coefficient of each term:
- \(14y\)
- \(15x^{2}\)
- \(a\)
Solution
- The coefficient of \(14y\) is \(14\)
- The coefficient of \(15x^{2}\) is \(15\)
- The coefficient of \(a\) is \(1\) since \(a=1a\).
Identify the coefficient of each term:
- \(17x\)
- \(41b^{2}\)
- \(z\)
- Answer
-
- \(14\)
- \(41\)
- \(1\)
Identify the coefficient of each term:
- \(9p\)
- \(13a^{2}\)
- \(y^{3}\)
- Answer
-
- \(9\)
- \(13\)
- \(1\)
Some terms share common traits. Look at the following 6 terms. Which ones seem to have traits in common?
\[5x \qquad 7 \qquad n^{2} \qquad 4 \qquad 3x \qquad 9n^{2}\nonumber\]
The \(7\) and the \(4\) are both constant terms.
The \(5x\) and the \(3x\) are both terms with \(x\).
The \(n^{2}\) and the \(9n^{2}\) are both terms with \(n^{2}\).
When two terms are constants or have the same variable and exponent, we say they are like terms.
- \(7\) and \(4\) are like terms.
- \(5x\) and \(3x\) are like terms.
- \(x^{2}\) and \(9x^{2}\) are like terms.
Terms that are either constants or have the same variables raised to the same powers are called like terms.
Identify the like terms: \(y^{3},7x^{2}, 14, 23, 4y^{3}, 9x, 5x^{2}\).
Solution
\(y^{3}\) and \(4y^{3}\) are like terms because both have \(y^{3}\); the variable and the exponent match.
\(7x^{2}\) and \(5x^{2}\) are like terms because both have \(x^{2}\); the variable and the exponent match.
\(14\) and \(23\) are like terms because both are constants.
There is no other term like \(9x\).
Identify the like terms: \(9, 2x^{3},y^{2}, 8x^{3}, 15, 9y, 11y^{2}\).
- Answer
-
\(9\) and \(15\), \(y^{2}\) and \(11y^{2}\), \(2x^{3}\) and \(8x^{3}\)
Identify the like terms: \(4x^{3},8x^{2}, 19, 3x^{3}, 24, 6x^{3}\).
- Answer
-
\(19\) and \(24\), \(8x^{2}\) and \(3x^{2}\), \(4x^{3}\) and \(6x^{3}\)
Adding or subtracting terms forms an expression. In the expression \(2x^{2} + 3x + 8\), from Example, the three terms are \(2x^{2}\), \(3x\), and \(8\).
Identify the terms in each expression.
- \(9x^{2}+7x+12\)
- \(8x+3y\)
Solution
- The terms of \(9x^{2}+7x+12\) are \(9x^{2}, 7x\), and \(12\).
- The terms of \(8x+3y\) are \(8x\) and \(3y\).
Identify the terms in the expression \(4x^{2}+5x+17\).
- Answer
-
\(4x^{2}, 5x, 17\)
Identify the terms in the expression \(5x+2y\).
- Answer
-
\(5x, 2y\)
If there are like terms in an expression, you can simplify the expression by combining the like terms. What do you think \(4x+7x+x\) would simplify to? If you thought \(12x\), you would be right!
\[\begin{array} { c } { 4 x + 7 x + x } \\ { x + x + x + x \quad + x + x + x + x + x + x + x \quad+ x } \\ { 12 x } \end{array}\]
Add the coefficients and keep the same variable. It doesn’t matter what x is—if you have 4 of something and add 7 more of the same thing and then add 1 more, the result is 12 of them. For example, 4 oranges plus 7 oranges plus 1 orange is 12 oranges. We will discuss the mathematical properties behind this later.
Simplify: \(4x+7x+x\)
Add the coefficients. \(12x\)
Simplify: \(2x^{2} + 3x + 7 + x^{2} + 4x + 5\)
Solution


Simplify: \(3x^{2} + 7x + 9 + 7x^{2} + 9x + 8\).
- Answer
-
\(10x^{2}+16x+17\)
Simplify: \(4y^{2} + 5y + 2 + 8y^{2} + 4y + 5\).
- Answer
-
\(12y^{2}+9y+7\)
- Identify like terms.
- Rearrange the expression so like terms are together.
- Add or subtract the coefficients and keep the same variable for each group of like terms.
Translate an English Phrase to an Algebraic Expression
In the last section, we listed many operation symbols that are used in algebra, then we translated expressions and equations into English phrases and sentences. Now we’ll reverse the process. We’ll translate English phrases into algebraic expressions. The symbols and variables we’ve talked about will help us do that. Table \(\PageIndex{7}\) summarizes them.
| Operation | Phrase | Expression |
|---|---|---|
| Addition | \(a\) plus \(b\) the sum of \(a\) and \(b\) \(a\) increased by \(b\) \(b\) more than \(a\) the total of \(a\) and \(b\) \(b\) added to \(a\) |
\[a+b\] |
| Subtraction | \(a\) minus \(b\) the difference of \(a\) and \(b\) \(a\) decreased by \(b\) \(b\) less than \(a\) \(b\) subtracted from \(a\) |
\[a−b\] |
| Multiplication | \(a\) times \(b\) the product of \(a\) and \(b\) twice \(a\) |
\[a\cdot b, ab, a(b), (a)(b)\] \[2a\] |
| Division | \(a\) divided by \(b\) the quotient of \(a\) and \(b\) the ratio of \(a\) and \(b\) \(b\) divided into \(a\) |
\[a\div b, a/b, \frac{a}{b}, b \enclose{longdiv}{a}\] |
Look closely at these phrases using the four operations:

Each phrase tells us to operate on two numbers. Look for the words of and and to find the numbers.
Translate each English phrase into an algebraic expression:
- the difference of \(17x\) and \(5\)
- the quotient of \(10x^{2}\) and \(7\).
Solution
- The key word is difference, which tells us the operation is subtraction. Look for the words of and and to find the numbers to subtract.
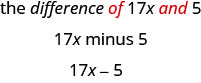
- The key word is “quotient,” which tells us the operation is division.
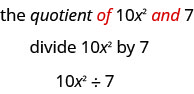
This can also be written \(10x^{2}/7\) or \(\dfrac{10x^{2}}{7}\).
Translate each English phrase into an algebraic expression:
- the difference of \(14x^{2}\) and \(13\)
- the quotient of \(12x\) and \(2\).
- Answer
-
- \(14x^{2} - 13\)
- \(12x \div 2\)
Translate each English phrase into an algebraic expression:
- the sum of \(17y^{2}\) and \(19\)
- the product of \(7\) and \(y\).
- Answer
-
- \(17y^{2} + 19\)
- \(7y\)
How old will you be in eight years? What age is eight more years than your age now? Did you add 8 to your present age? Eight “more than” means 8 added to your present age. How old were you seven years ago? This is 7 years less than your age now. You subtract 7 from your present age. Seven “less than” means 7 subtracted from your present age.
Translate the English phrase into an algebraic expression:
- Seventeen more than \(y\)
- Nine less than \(9x^{2}\).
Solution
- The key words are more than. They tell us the operation is addition. More than means “added to.”
\(\begin{array} { c } { \text { Seventeen more than } y } \\ { \text { Seventeen added to } y } \\ { y + 17 } \end{array}\)
- The key words are less than. They tell us to subtract. Less than means “subtracted from.”
\(\begin{array} { c } { \text { Nine less than } 9 x ^ { 2 } } \\ { \text { Nine subtracted from } 9 x ^ { 2 } } \\ { 9 x ^ { 2 } - 9 } \end{array}\)
Translate the English phrase into an algebraic expression:
- Eleven more than x
- Fourteen less than \(11a\).
- Answer
-
- \(x+11\)
- \(11a−14\)
Translate the English phrase into an algebraic expression:
- \(13\) more than \(z\)
- \(18\) less than \(8x\).
- Answer
-
1. \(z+13\)
2. \(8x−18\)
Translate the English phrase into an algebraic expression:
- five times the sum of \(m\) and \(n\)
- the sum of five times \(m\) and \(n\).
Solution
There are two operation words—times tells us to multiply and sum tells us to add.
1. Because we are multiplying \(5\) times the sum we need parentheses around the sum of \(m\) and \(n\), \((m+n)\). This forces us to determine the sum first. (Remember the order of operations.)
\[\begin{array} { c } { \text { five times the sum of } m \text { and } n } \\ { 5 ( m + n ) } \end{array}\]
2. To take a sum, we look for the words “of” and “and” to see what is being added. Here we are taking the sum of five times \(m\) and \(n\.)\[\begin{array} { c } { \text { the sum of five times } m \text { and } n } \\ { 5 m + n } \end{array}\]
Translate the English phrase into an algebraic expression:
- four times the sum of \(p\) and \(q\)
- the sum of four times \(p\) and \(q\).
- Answer
-
- \(4(p+q)\)
- \(4p+q\)
Translate the English phrase into an algebraic expression:
- the difference of two times x and \(8\),
- two times the difference of x and \(8\).
- Answer
-
- \(2x−8\)
- \(2(x−8)\)
Later in this course, we’ll apply our skills in algebra to solving applications. The first step will be to translate an English phrase to an algebraic expression. We’ll see how to do this in the next two examples.
The length of a rectangle is \(6\) less than the width. Let \(w\) represent the width of the rectangle. Write an expression for the length of the rectangle.
Solution
\[\begin{array} { l l } { \text { Write a phrase about the length of the rectangle. } } &{ 6 \text { less than the width } } \\ { \text { Substitute } w \text { for "the width." } } &{\text{6 less then w}} \\ { \text { Rewrite "less than" as "subtracted from." } } &{\text{6 subtracted from w}} \\ { \text { Translate the phrase into algebra. } } &{w - 6} \end{array}\]
The length of a rectangle is \(7\) less than the width. Let \(w\) represent the width of the rectangle. Write an expression for the length of the rectangle.
- Answer
-
\(w - 7\)
The width of a rectangle is \(6\) less than the length. Let \(l\) represent the length of the rectangle. Write an expression for the width of the rectangle.
- Answer
-
\(l - 6\)
June has dimes and quarters in her purse. The number of dimes is three less than four times the number of quarters. Let \(q\) represent the number of quarters. Write an expression for the number of dimes.
Solution
\[\begin{array} { ll } { \text { Write the phrase about the number of dimes. } } &{\text{three less than four times the number of quarters}} \\ { \text { Substitute } q \text { for the number of quarters. } } &{\text{3 less than 4 times q}} \\ { \text { Translate "4 times } q \text { ." } } &{\text{3 less than 4q}} \\ { \text { Translate the phrase into algebra. } } &{\text{4q - 3}} \end{array}\]
Geoffrey has dimes and quarters in his pocket. The number of dimes is eight less than four times the number of quarters. Let \(q\) represent the number of quarters. Write an expression for the number of dimes.
- Answer
-
\(4q - 8\)
Lauren has dimes and nickels in her purse. The number of dimes is three more than seven times the number of nickels. Let \(n\) represent the number of nickels. Write an expression for the number of dimes.
- Answer
-
\(7n + 3\)
Key Concepts
- Notation The result is…
\(\begin{array} { l l } {\bullet \space a + b } &{ \text { the sum of } a \text { and } b } \\ { \bullet \space a - b } &{ \text { the difference of } a \text { and } b } \\ {\bullet\space a \cdot b , a b , ( a ) ( b ) ( a ) b , a ( b ) } &{ \text { the product of } a \text { and } b } \\ {\bullet\space a \div b , a / b , \frac { a } { b } , b ) \overline{a} } &{ \text { the quotient of } a \text { and } b } \end{array}\) - Inequality
\(\begin{array} { l l } { \bullet \space a < b \text { is read "a is less than } b ^ { \prime \prime } } &{a \text { is to the left of } b \text { on the number line } } \\ { \bullet \space a > b \text { is read "a is greater than } b ^ { \prime \prime } } & { a \text { is to the right of } b \text { on the number line } } \end{array}\) - Inequality Symbols Words
\(\begin{array} {ll} { \bullet a \neq b } &{ a \text { is not equal to } b } \\ { \bullet a < b } &{ a \text { is less than } b } \\ { \bullet a \leq b } &{ a \text { is less than or equal to } b } \\ { \bullet a > b } & { a \text { is greater than } b } \\ { \bullet a \geq b } & { a \text { is greater than or equal to } b } \end{array}\) - Grouping Symbols
- Parentheses ()
- Brackets []
- Braces {}
- Exponential Notation
- \(a^{n}\) means the product of \(n\) factors of \(a\). The expression \(a^{n}\) is read \(a\) to the \(n^{th}\) power.
- Order of Operations: When simplifying mathematical expressions perform the operations in the following order:
- Parentheses and other Grouping Symbols: Simplify all expressions inside the parentheses or other grouping symbols, working on the innermost parentheses first.
- Exponents: Simplify all expressions with exponents.
- Multiplication and Division: Perform all multiplication and division in order from left to right. These operations have equal priority.
- Addition and Subtraction: Perform all addition and subtraction in order from left to right. These operations have equal priority.
- Combine Like Terms
- Identify like terms.
- Rearrange the expression so like terms are together.
- Add or subtract the coefficients and keep the same variable for each group of like terms.
Glossary
- coefficient
- The coefficient of a term is the constant that multiplies the variable in a term.
- constant
- A constant is a number whose value always stays the same.
- equality symbol
- The symbol “\(=\)” is called the equal sign. We read \(a=b\) as “\(a\) is equal to \(b\).”
- equation
- An equation is two expressions connected by an equal sign.
- evaluate an expression
- To evaluate an expression means to find the value of the expression when the variable is replaced by a given number.
- expression
- An expression is a number, a variable, or a combination of numbers and variables using operation symbols.
- like terms
- Terms that are either constants or have the same variables raised to the same powers are called like terms.
- simplify an expression
- To simplify an expression, do all operations in the expression.
- term
- A term is a constant or the product of a constant and one or more variables.
- variable
- A variable is a letter that represents a number whose value may change.


