1.4: Add and Subtract Integers
- Page ID
- 15119
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use negatives and opposites
- Simplify: expressions with absolute value
- Add integers
- Subtract integers
A more thorough introduction to the topics covered in this section can be found in the Prealgebra chapter, Integers.
Use Negatives and Opposites
Our work so far has only included the counting numbers and the whole numbers. But if you have ever experienced a temperature below zero or accidentally overdrawn your checking account, you are already familiar with negative numbers. Negative numbers are numbers less than \(0\). The negative numbers are to the left of zero on the number line. See Figure \(\PageIndex{1}\).
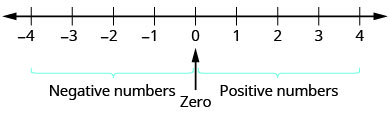
The arrows on the ends of the number line indicate that the numbers keep going forever. There is no biggest positive number, and there is no smallest negative number.
Is zero a positive or a negative number? Numbers larger than zero are positive, and numbers smaller than zero are negative. Zero is neither positive nor negative.
Consider how numbers are ordered on the number line. Going from left to right, the numbers increase in value. Going from right to left, the numbers decrease in value. See Figure \(\PageIndex{2}\).
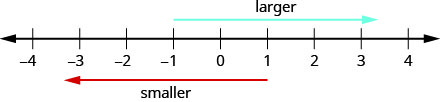
Doing the Manipulative Mathematics activity “Number Line-part 2” will help you develop a better understanding of integers.
Remember that we use the notation:
\(a \lt b\) (read “\(a\) is less than \(b\)”) when \(a\) is to the left of \(b\) on the number line.
\(a \gt b\) (read “\(a\) is greater than \(b\)”) when \(a\) is to the right of \(b\) on the number line.
Now we need to extend the number line which showed the whole numbers to include negative numbers, too. The numbers marked by points in Figure \(\PageIndex{3}\). are called the integers. The integers are the numbers \(...−3, −2, −1, 0, 1, 2, 3…\)

Order each of the following pairs of numbers, using \(<\) or \(>\):
- \(14 \; \_\_\_\; 6\)
- \(-1\; \_\_\_ \;9\)
- \(-1\; \_\_\_ -4\)
- \(\;\; 2 \;\_\_\_ -20\)
Solution:
It may be helpful to refer to the number line shown.

Figure \(\PageIndex{4}\)
\( \begin{align*}1. \quad & 14\;\_\_\_\;6 \\[4pt]
& 14 > 6 && \text{\(14\) is to the right of \(6\) on the number line.} \\[8pt]
2. \quad & -1\;\_\_\_\;9 \\[4pt]
& -1 < 9 && \text{\(-1\) is to the left of \(9\) on the number line.}\\[8pt]
3. \quad & -1\;\_\_\_-4 \\[4pt]
& -1 > -4 && \text{\(-1\) is to the right of \(-4\) on the number line.}\\[8pt]
4. \quad & 2\;\_\_\_-20 \\[4pt]
& 2 > -20 && \text{\(2\) is to the right of \(-20\) on the number line.}\
\end{align*} \)
Order each of the following pairs of numbers, using \(<\) or \(>\):
- \(15 \; \_\_\_\; 7\)
- \(-2 \; \_\_\_\; 5\)
- \(-3 \; \_\_\_\; -7\)
- \(5 \; \_\_\_\; -17\)
- Answer
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
Order each of the following pairs of numbers, using \(<\) or \(>\):
- \(8 \; \_\_\_\; 13\)
- \(3 \; \_\_\_\; -4\)
- \(-5 \; \_\_\_\; -2\)
- \(9 \; \_\_\_\; -21\)
- Answer
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
You may have noticed that, on the number line, the negative numbers are a mirror image of the positive numbers, with zero in the middle. Because the numbers \(2\) and \(−2\) are the same distance from zero, they are called opposites. The opposite of \(2\) is \(−2\), and the opposite of \(−2\) is \(2\).
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.
Figure \(\PageIndex{5}\) illustrates the definition.

Sometimes in algebra the same symbol has different meanings. Just like some words in English, the specific meaning becomes clear by looking at how it is used. You have seen the symbol “\(−\)” used in three different ways.
\[\begin{align*} &10 − 4 \quad \text{Between two numbers, it indicates the operation of }\textit{subtraction}.\\ & \qquad \qquad \text{We read } 10 - 4 \, \text{as “}10 \, \text{minus} \, 4.\text{”}\\[5pt]
&-8 \quad \text{In front of a number, it indicates a }\textit{negative}\text{ number.}\\ & \qquad \qquad \text{We read} -8 \text{ as “negative eight.”}\\[5pt]
&-x \quad \text{In front of a variable, it indicates the }\textit{opposite.} \\ & \qquad \qquad \text{We read } -x \text{ as “the opposite of } x\text{”}\\[5pt]
&-(-2) \quad \text{Here there are two “−” signs.}\\
& \qquad \qquad \text{The one in the parentheses tells us the number is negative }2. \\
& \qquad \qquad \text{ The one outside the parentheses tells us to take the }\textit{opposite}\text{ of }−2. \\
& \qquad \qquad \text{ We read }−(−2) \text{ as “the opposite of negative two.”} \end{align*}\]
\(−a\) means the opposite of the number \(a\).
The notation \(−a\) is read as “the opposite of \(a\).”
Find:
- the opposite of \(7\)
- the opposite of \(−10\)
- the opposite of \(−(−6)\)
Solution:
1.\( \quad −7\) is the same distance from \(0\) as \(7\), but on the opposite side of \(0\). The opposite of \(7\) is \(-7\).

2.\( \quad 10\) is the same distance from \(0\) as \(−10\), but on the opposite side of \(0\). The opposite of \(-10\) is \(10\).

3. \(\quad\)The opposite of \(-(-6)\) is \(-6\).

Find:
- the opposite of \(4\)
- the opposite of \(−3\)
- \(−(−1)\)
- Answer
-
- \(-4\)
- \(3\)
- \(1\)
Find:
- the opposite of \(8\)
- the opposite of \(−5\)
- \(−(−5)\)
- Answer
-
- \(-8\)
- \(5\)
- \(5\)
Our work with opposites gives us a way to define the integers. The whole numbers and their opposites are called the integers. The integers are the numbers \(…−3,−2,−1,0,1,2,3…\)
The whole numbers and their opposites are called the integers.
The integers are the numbers
\[…−3,−2,−1,0,1,2,3… \nonumber \]
When evaluating the opposite of a variable, we must be very careful. Without knowing whether the variable represents a positive or negative number, we don’t know whether −x−x is positive or negative. We can see this in Example \(\PageIndex{1}\).
Evaluate
- \(-x\), when \(x = 8\)
- \(-x\), when \(x = -8\)
Solution:
-

-x 
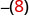
Write the opposite of 8. -8 -

-x 
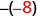
Write the opposite of -8. 8
Evaluate \(-n\), when
- \(n = 4\)
- \(n = -4\)
- Answer
-
- \(-4\)
- \(4\)
Evaluate \(-m\), when
- \(m = 11\)
- \(m = -11\)
- Answer
-
- \(-11\)
- \(11\)
Simplify: Expressions with Absolute Value
We saw that numbers such as \(2\) and \(−2\) are opposites because they are the same distance from \(0\) on the number line. They are both two units from \(0\). The distance between \(0\) and any number on the number line is called the absolute value of that number.
The absolute value of a number is its distance from \(0\) on the number line.
The absolute value of a number \(n\) is written as \(|n|\).
For example,
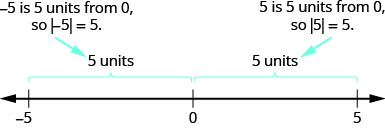
- \(−5\) is \(5\) units away from \(0\), so \(|−5|=5\).
- \(5\) is \(5\) units away from \(0\), so \(|5|=5\).
Figure \(\PageIndex{6}\) illustrates this idea.
The absolute value of a number is never negative (because distance cannot be negative). The only number with absolute value equal to zero is the number zero itself, because the distance from \(0\) to \(0\) on the number line is zero units.
\(|n| \geq 0\) for all numbers
Absolute values are always greater than or equal to zero!
Mathematicians say it more precisely, “absolute values are always non-negative.” Non-negative means greater than or equal to zero.
Simplify:
- \(|3|\)
- \(|-44|\)
- \(|0|\)
Solution:
The absolute value of a number is the distance between the number and zero. Distance is never negative, so the absolute value is never negative.
- \( |3| = 3\)
- \(|-44| = 44\)
- \( |0| = 0\)
Simplify:
- \(|4|\)
- \(|-28|\)
- \(|0|\)
- Answer
-
- \(4\)
- \(28\)
- \(0\)
Simplify:
- \(|-13|\)
- \(|47|\)
- Answer
-
- \(13\)
- \(47\)
In the next example, we’ll order expressions with absolute values. Remember, positive numbers are always greater than negative numbers!
Fill in \(<, >, \text{or} =\) for each of the following pairs of numbers:
- \(|−5| \; {\underline{\hspace {2 em}}} \;−|−5|\)
- \(8 \;{\underline{\hspace {2 em}}} \;−|−8|\)
- \(-9 \;{\underline{\hspace {2 em}}} \;−|−9|\)
- \(-(-16) \;{\underline{\hspace {2 em}}}\; −|−16|\)
Solution:
\(\begin{array} {llll} {\text{Simplification}} &{|-5|} & {\underline{\hspace {2 em}}} &{-|-5|} \\ {\text{Order.}} &{5} &{\underline{\hspace {2 em}}} &{-5} \\ {} &{5} &{>} &{-5} \\ {} &{|-5|} &{>} &{-|-5|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{8} & {\underline{\hspace {2 em}}} &{-|-8|} \\ {\text{Order.}} &{8} &{\underline{\hspace {2 em}}} &{-8} \\ {} &{8} &{>} &{-8} \\ \text{so }\\ {} & {|8|} &{>} &{-|-8|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-9} & {\underline{\hspace {2 em}}} &{-|-9|} \\ {\text{Order.}} &{-9} &{\underline{\hspace {2 em}}} &{-9} \\ {} &{-9} &{=} &{-9} \\ \text{so } \\ {} & {-9} &{=} &{-|-9|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-(-16)} & {\underline{\hspace {2 em}}} &{-|16|} \\ {\text{Order.}} &{16} &{\underline{\hspace {2 em}}} &{-16} \\ {} &{16} &{>} &{-16} \\ \text{so } \\ {} & {-(-16)} &{>} &{-|-16|} \\ \end{array}\)
Fill in \(<, >, \text{or} =\) for each of the following pairs of numbers:
- \(|−9| \;{\underline{\hspace {2 em}}} \; −|−9|\)
- \(2 \;{\underline{\hspace {2 em}}} \; −|−2|\)
- \(-8 \;{\underline{\hspace {2 em}}} \; −|−8|\)
- \(-(-9) \;{\underline{\hspace {2 em}}} \; −|−9|\)
- Answer
-
- \(>\)
- \(>\)
- \(<\)
- \(>\)
Fill in \(<, >, \text{or} =\) for each of the following pairs of numbers:
- \(7 \;{\underline{\hspace {2 em}}} \; −|−7|\)
- \(-(-10) \;{\underline{\hspace {2 em}}} \; −|−10|\)
- \(|-4| \;{\underline{\hspace {2 em}}} \; −|−4|\)
- \(-1 \;{\underline{\hspace {2 em}}} \; |−1|\)
- Answer
-
- \(>\)
- \(>\)
- \(>\)
- \(<\)
We now add absolute value bars to our list of grouping symbols. When we use the order of operations, first we simplify inside the absolute value bars as much as possible, then we take the absolute value of the resulting number.
\[\begin{array} {llll} {\text{Parentheses}} &{()} & {\text{Braces}} & {\{\}} \\ {\text{Brackets}} &{[\space]} &{\text{Absolute}} &{|\space|} \\ \end{array} \nonumber\]
In the next example, we simplify the expressions inside absolute value bars first, just like we do with parentheses.
Simplify: \(24 - |19 - 3(6 - 2)|\)
Solution:
\[\begin{array} {ll} {} &{24 - |19 - 3(6 - 2)|} \\ {\text{Work inside parentheses first: subtract } 2\space \text{from } 6} &{24 - |19 - 3(4)|} \\ {\text{Multiply }3(4)} &{24 - |19 - 12|} \\ {\text{Subtract inside the absolute value bars. }} &{24 - |7|} \\ {\text{Take the absolute value.}} &{24 - 7} \\ {\text{Subtract.}} &{17} \end{array}\nonumber\]
Simplify: \(19 - |11 - 4(3 - 1)|\)
- Answer
-
\(16\)
Simplify: \(9 - |8 - 4(7 - 5)|\)
- Answer
-
\(9\)
Evaluate:
- \(|x|\) when \(x = -35\)
- \(|y|\) when \(y = -20\)
- \(-|u|\) when \(u = 12\)
- \(-|p|\) when \(p = -14\)
Solution:
1. \(|x|\) when \(x = -35\)
\(\begin{array} {ll} {} &{|x|} \\ {\text{Substitute } -35 \space \text{for }x} &{|-35|} \\ {\text{Take the absolute value.}} &{35} \end{array}\)
2. \(|y|\) when \(y = -20\)
\(\begin{array} {ll} {} &{|-y|} \\ {\text{Substitute } -20 \space \text{for }y} &{|-(-20)|} \\ {\text{Simplify}} &{|20|} \\ {\text{Take the absolute value.}} &{20} \end{array}\)
3. \(-|u|\) when \(u = 12\)
\(\begin{array} {ll} {} &{-|u|} \\ {\text{Substitute } 12 \space \text{for }u} &{|-12|} \\ {\text{Take the absolute value.}} &{-12} \end{array}\)
4. \(-|p|\) when \(p = -14\)
\(\begin{array} {ll} {} &{-|p|} \\ {\text{Substitute } -14 \space \text{for }p} &{-|-14|} \\ {\text{Take the absolute value.}} &{-14} \end{array}\)
Evaluate:
- \(|x|\) when \(x = -17\)
- \(|y|\) when \(y = -39\)
- \(-|m|\) when \(m = 22\)
- \(-|p|\) when \(p = -11\)
- Answer
-
- \(17\)
- \(39\)
- \(-22\)
- \(-11\)
Evaluate:
- \(|y|\) when \(y = -23\)
- \(|-y|\) when \(y = -21\)
- \(-|n|\) when \(n = 37\)
- \(-|q|\) when \(q = -49\)
- Answer
-
- \(23\)
- \(21\)
- \(-37\)
- \(-49\)
Add Integers
Most students are comfortable with the addition and subtraction facts for positive numbers. But doing addition or subtraction with both positive and negative numbers may be more challenging.
Doing the Manipulative Mathematics activity “Addition of Signed Numbers” will help you develop a better understanding of adding integers.”
We will use two color counters to model addition and subtraction of negatives so that you can visualize the procedures instead of memorizing the rules.
We let one color (blue) represent positive. The other color (red) will represent the negatives. If we have one positive counter and one negative counter, the value of the pair is zero. They form a neutral pair. The value of this neutral pair is zero.
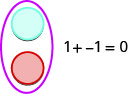
We will use the counters to show how to add the four addition facts using the numbers \(5, −5\) and \(3,−3\).
\[\begin{array} {llll} {5 + 3} &{-5 + (-3)} &{-5 + 3} &{5 + (-3)} \end{array} \nonumber \]
To add \(5+3\), we realize that \(5+3\) means the sum of \(5\) and \(3\).
| We start with \(5\) positives. |  |
| And then we add \(3\) positives. |  |
| We now have \(8\) positives. The sum of \(5\) and \(3\) is \(8\). |  |
Now we will add \(−5 + (−3)\). Watch for similarities to the last example \(5 + 3 = 8\).
To add \(−5 + (−3)\), we realize this means the sum of \(−5\) and \(−3\).
| We start with \(5\) negatives. |  |
| And then we add \(3\) negatives. |  |
| We now have \(8\) negative. The sum of \(-5\) and \(-3\) is \(-8\). |  |
In what ways were these first two examples similar?
- The first example adds \(5\) positives and \(3\) positives—both positives.
- The second example adds \(5\) negatives and \(3\) negatives—both negatives.
In each case we got \(8\) — either \(8\) positives or \(8\) negatives.
When the signs were the same, the counters were all the same color, and so we added them.

Add:
- \(1 + 4\)
- \(-1 + (-4)\)
Solution:
1. 
\(1\) positive plus \(4\) positives is \(5\) positives.
2. 
\(1\) negative plus \(4\) negatives is \(5\) negatives.
Add:
- \(2 + 4\)
- \(-2 + (-4)\)
- Answer
-
- \(6\)
- \(-6\)
Add:
- \(2 + 5\)
- \(-2 + (-5)\)
- Answer
-
- \(7\)
- \(-7\)
So what happens when the signs are different? Let’s add \(−5+3\). We realize this means the sum of \(−5\) and \(3\). When the counters were the same color, we put them in a row. When the counters are a different color, we line them up under each other.
| \(-5 + 3\) means the sum of \(-5\) and \(3\). | |
| We start with \(5\) negatives. |  |
| And then we add \(3\) positives. |  |
| We remove any neutral pairs. |  |
| We have \(2\) negatives left. |  |
| The sum of \(-5\) and \(3\) is \(-2\). | \(-5 + 3 = 2\) |
Notice that there were more negatives than positives, so the result was negative.
Let’s now add the last combination, \(5+(−3)\).
| \(5 + (-3)\) means the sum of \(-5\) and \(-3\). | |
| We start with \(5\) positives. |  |
| And then we add \(3\) negatives. | 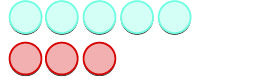 |
| We remove any neutral pairs. | 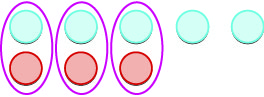 |
| We have \(2\) positives left. |  |
| The sum of \(5\) and \(-3\) is \(2\). | \(5 + (-3) = 2\) |
When we use counters to model addition of positive and negative integers, it is easy to see whether there are more positive or more negative counters. So we know whether the sum will be positive or negative.
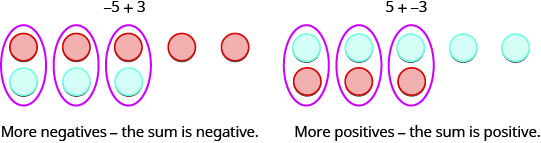
Add:
- \(-1 + 5\)
- \(1 + (-5)\)
Solution:
1. \(-1 + 5\)

There are more positives, so the sum is positive.
So, \(-1 + 5 = 4\).
2. \(1 + (-5)\)

There are more negatives, so the sum is negative.
So, \(1 + (-5) = -4\)
Add:
- \(-2 + 4\)
- \(2 + (-4)\)
- Answer
-
- \(2\)
- \(-2\)
Add:
- \(-2 + 5\)
- \(2 + (-5)\)
- Answer
-
- \(3\)
- \(-3\)
Now that we have added small positive and negative integers with a model, we can visualize the model in our minds to simplify problems with any numbers.
When you need to add numbers such as \(37+(−53)\), you really don’t want to have to count out \(37\) blue counters and \(53\) red counters. With the model in your mind, can you visualize what you would do to solve the problem?
Picture \(37\) blue counters with \(53\) red counters lined up underneath. Since there would be more red (negative) counters than blue (positive) counters, the sum would be negative. How many more red counters would there be? Because \(53−37=16\), there are \(16\) more red counters.
Therefore, the sum of \(37+(−53)\) is \(−16\).
\[37+(−53)=−16\nonumber\]
Let’s try another one. We’ll add \(−74+(−27)\). Again, imagine \(74\) red counters and \(27\) more red counters, so we’d have \(101\) red counters. This means the sum is \(−101\).
\[−74+(−27)=−101\nonumber\]
Let’s look again at the results of adding the different combinations of \(5,−5\) and \(3, -3\).
\[\begin{array} {ll} {5 + 3=8} &{-5 + (-3)=-8} \\{\text{both positive, sum positive}} &{\text{both negative, sum negative}} \end{array}\nonumber\]
When the signs are the same, the counters would be all the same color, so add them.
\[\begin{array} {ll} {-5 + 3=-2} &{5 + (-3)=2} \\{\text{different signs, more negatives, sum negative}} &{\text{different signs, more positives, sum positive}} \end{array}\nonumber\]
When the signs are different, some of the counters would make neutral pairs, so subtract to see how many are left.
Visualize the model as you simplify the expressions in the following examples.
Simplify:
- \(19 + (-47)\)
- \(-14 + (-36)\)
Solution:
1. Since the signs are different, we subtract \(19\) from \(47\). The answer will be negative because there are more negatives than positives.
\(\text{Add.} \qquad 19 + (-47) = -28\)
2. Since the signs are same, we add. The answer will be negative because there are more negatives than positives.
\(\text{Add.} \qquad-14 + (-36) = -50\)
Simplify:
- \(-31 + (-19)\)
- \(15 + (-32)\)
- Answer
-
- \(-50\)
- \(-17\)
Simplify:
- \(-42 + (-28)\)
- \(25 + (-61)\)
- Answer
-
- \(-70\)
- \(-36\)
The techniques used up to now extend to more complicated problems, like the ones we’ve seen before. Remember to follow the order of operations!
Simplify:
\(-5 + 3(-2 + 7)\)
Solution:
\[\begin{array} {ll} {} &{-5 + 3(-2 + 7)} \\ {\text{Simplify inside the parenthesis}} &{-5 + 3(5)} \\{\text{Multiply}} &{-5 + 15} \\{\text{add left to right}} &{10} \end{array}\nonumber\]
Simplify:
\(-2 + 5(-4 + 7)\)
- Answer
-
\(13\)
Simplify:
\(-4 + 2(-3 + 5)\)
- Answer
-
\(0\)
Subtract Integers
Doing the Manipulative Mathematics activity “Subtraction of Signed Numbers” will help you develop a better understanding of subtracting integers.
We will continue to use counters to model the subtraction. Remember, the blue counters represent positive numbers and the red counters represent negative numbers.
Perhaps when you were younger, you read “\(5−3\)” as “\(5\) take away \(3\).” When you use counters, you can think of subtraction the same way!
We will model the four subtraction facts using the numbers \(5\) and \(3\).
\[\begin{array} {llll} {5 - 3} &{-5 - (-3))} &{-5 -3} &{5 - (-3)} \end{array}\nonumber\]
To subtract \(5−3\), we restate the problem as “\(5\) take away \(3\).”
| We start with \(5\) positives. |  |
| We 'take away' \(3\) positives. |  |
| We have \(2\) positives left. | |
| The difference of \(5\) and \(3\) is \(2\). | \(2\) |
Now we will subtract \(−5−(−3)\). Watch for similarities to the last example \(5−3=2\).
To subtract \(−5−(−3)\), we restate this as “\(–5\) take away \(–3\)”
| We start with \(5\) negatives. |  |
|
We 'take away' \(3\) negatives. |
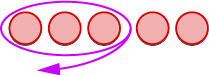 |
| We have \(2\) negatives left. | |
| The difference of \(-5\) and \(-3\) is \(-2\). |
\(-2\) |
Notice that these two examples are much alike: The first example, we subtract 3 positives from 5 positives and end up with 2 positives.
In the second example, we subtract 3 negatives from 5 negatives and end up with 2 negatives.
Each example used counters of only one color, and the “take away” model of subtraction was easy to apply.
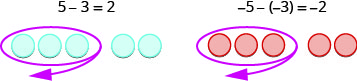
Subtract:
- \(7 - 5\)
- \(-7 - (-5)\)
Solution:
- \[\begin{array} {ll} {7 - 5} \\ {2}&{\text{Take }5\space \text{positives from }7 \space \text{positives and get }2\space \text{positives}} & \end{array}\nonumber\]
- \[\begin{array} {ll} {-7 - (-5)} \\ {-2} &{\text{Take }5\space \text{negatives from }7 \space \text{negatives and get }2\space \text{negatives}} \end{array}\nonumber\]
Subtract:
- \(6 - 4\)
- \(-6 - (-4)\)
- Answer
-
- \(2\)
- \(-2\)
Subtract:
- \(7 - 4\)
- \(-7 - (-4)\)
- Answer
-
- \(3\)
- \(-3\)
What happens when we have to subtract one positive and one negative number? We’ll need to use both white and red counters as well as some neutral pairs. Adding a neutral pair does not change the value. It is like changing quarters to nickels—the value is the same, but it looks different.
- To subtract \(−5−3\), we restate it as \(−5\) take away \(3\).
We start with \(5\) negatives. We need to take away \(3\) positives, but we do not have any positives to take away.
Remember, a neutral pair has value zero. If we add \(0\) to \(5\) its value is still \(5\). We add neutral pairs to the \(5\) negatives until we get \(3\) positives to take away.
| \(-5 -3\) means \(-5\) take away \(3\) | |
| We start with \(5\) negatives. |  |
| We now add the neutrals needed to get \(3\) positives. |  |
| We remove the \(3\) positives. | 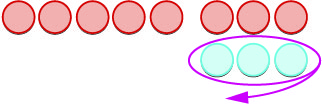 |
| We are left with \(8\) negatives. |  |
| The difference of \(-5\) and \(3\) is \(-8\). | \(-5 - 3 = -8\) |
And now, the fourth case, \(5−(−3)\). We start with \(5\) positives. We need to take away \(3\) negatives, but there are no negatives to take away. So we add neutral pairs until we have \(3\) negatives to take away.
| \(5 -(-3)\) means \(5\) take away \(-3\) | |
| We start with \(5\) positives. |  |
| We now add the needed neutrals pairs. |  |
| We remove the \(3\) negatives. | 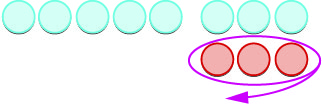 |
| We are left with \(8\) positives. |  |
| The difference of \(5\) and \(-3\) is \(8\). | \(5 - (-3) = 8\) |
Subtract:
- \(-3 -1\)
- \(3 - (-1)\)
Solution:
1.
|
Take 1 positive from the one added neutral pair. |
  |
\(\begin{array} {l} {-3 -1} \\ {-4} \end{array}\) |
|
Take 1 negative from the one added neutral pair. |
  |
\(\begin{array} {l} {3 - (-1)} \\ {4} \end{array}\) |
Subtract:
- \(-6 -4\)
- \(6 - (-4)\)
- Answer
-
- \(-10\)
- \(10\)
Subtract:
- \(-7-4\)
- \(7 - (-4)\)
- Answer
-
- \(-11\)
- \(11\)
Have you noticed that subtraction of signed numbers can be done by adding the opposite? In Exercise \(\PageIndex{33}\), \(−3−1\) is the same as \(−3+(−1)\) and \(3−(−1)\) is the same as \(3+1\). You will often see this idea, the subtraction property, written as follows:
\[a−b=a+(−b) \nonumber\]
Subtracting a number is the same as adding its opposite.
Look at these two examples.
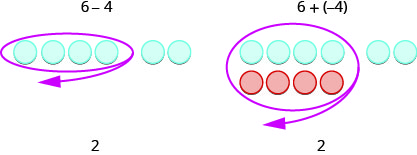
Of course, when you have a subtraction problem that has only positive numbers, like \(6−4\), you just do the subtraction. You already knew how to subtract \(6−4\) long ago. But knowing that \(6−4\) gives the same answer as \(6+(−4)\) helps when you are subtracting negative numbers. Make sure that you understand how \(6−4\) and \(6+(−4)\) give the same results!
Simplify:
- \(13 - 8 \space \text{and } 13 + (-8)\)
- \(-17 - 9 \space \text{and } -17 + (-9)\)
Solution:
- \(\begin{array} {llll} {\text{Subtract.}} &{13 - 8} &{\text{and}} &{13 + (-8)} \\ {} &{5} &{} &{5} \end{array}\)
- \(\begin{array} {llll} {\text{Subtract.}} &{-17 - 9} &{\text{and}} &{-17 + (-9)} \\ {} &{-26} &{} &{-26} \end{array}\)
Simplify:
- \(21 - 13 \space \text{and } 21 + (-13)\)
- \(-11 - 7 \space \text{and } -11 + (-7)\)
- Answer
-
- \(8\)
- \(-18\)
Simplify:
- \(15 - 7 \space \text{and } 15 + (-7)\)
- \(-14 - 8 \space \text{and } -14 + (-8)\)
- Answer
-
- \(8\)
- \(-22\)
Look at what happens when we subtract a negative.

Subtracting a negative number is like adding a positive!
You will often see this written as \(a−(−b)=a+b\).
Does that work for other numbers, too? Let’s do the following example and see.
Simplify:
- \(9 - (-15) \space \text{and } 9 + 15\)
- \(-7 - (-4) \space \text{and } -7 + 4\)
Solution:
- \(\begin{array} {lll} {} &{9 - (-15)} &{9 + 15} \\ {\text{Subtract}} &{24} &{24} \end{array}\)
- \(\begin{array} {lll} {} &{-7 - (-4)} &{-7 + 4} \\ {\text{Subtract}} &{-3} &{-3} \end{array}\)
Simplify:
- \(6 - (-13) \space \text{and } 6 + 13\)
- \(-5 - (-1) \space \text{and } -5 + 1\)
- Answer
-
- \(19\)
- \(-4\)
Simplify:
- \(4 - (-19) \space \text{and } 4 + 19\)
- \(-4 - (-7) \space \text{and } -4 + 7\)
- Answer
-
- \(23\)
- \(3\)
Let’s look again at the results of subtracting the different combinations of \(5,−5\) and \(3,−3\).
\[\begin{array} {l} {5 - 3} &{-5 - (-3)} \\ {2} &{-2} \\ {5\space\text{positives take away }3\space\text{positives}} &{5\space\text{negatives take away }3\space\text{negatives}} \\ {2\space\text{positives}} &{2\space\text{negatives}} \end{array}\nonumber\]
When there would be enough counters of the color to take away, subtract.
\[\begin{array} {l} {-5 - 3} &{5 - (-3)} \\ {-8} &{8} \\ {5\space\text{negatives, want to take away }3\space\text{positives}} &{5\space\text{positives, want to take away }3\space\text{negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}} \end{array}\nonumber\]
When there would be not enough counters of the color to take away, add.
What happens when there are more than three integers? We just use the order of operations as usual.
Simplify:
\(7 - (-4 -3) - 9\)
Solution:
\[ \begin{array} {ll} {} &{7 - (-4 - 3) - 9} \\ {\text{Simplify inside the parenthesis first.}} &{7 - (-7) - 9} \\ {\text{Subtract left to right.}} &{14 - 9} \\ {\text{Subtract}} &{5} \end{array}\nonumber\]
Simplify:
\(8−(−3−1)−9\)
- Answer
-
\(3\)
Simplify:
\(12−(−9−6)−14\)
- Answer
-
\(12\)
Access these online resources for additional instruction and practice with adding and subtracting integers. You will need to enable Java in your web browser to use the applications.
Key Concepts
- Addition of Positive and Negative Integers
\[\begin{array} {ll} {5 + 3} &{-5+(-3)} \\ {8} &{-8} \\ {\text{both positive,}} &{\text{both negative,}} \\ {\text{sum positive}} &{\text{sum negative}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 + 3} &{5+(-3)} \\ {-2} &{2} \\ {\text{different signs,}} &{\text{different signs,}} \\ {\text{more negatives}} &{\text{more positives}} \\ {\text{sum negative}} &{\text{sum positive}} \end{array}\nonumber\]
- Property of Absolute Value:
\(|n| \geq 0\) for all numbers. Absolute values are always greater than or equal to zero!
- Subtraction of Integers
\[\begin{array} {ll} {5 - 3} &{-5-(-3)} \\ {2} &{-2} \\ {5\space\text{positives}} &{5\space\text{negatives}} \\ {\text{take away 3 positives}} &{\text{take away 3 negatives}} \\ {\text{2 positives}} &{\text{2 negatives}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 - 3} &{5-(-3)} \\ {-8} &{8} \\ {\text{5 negatives, want to}} &{\text{5 positives, want to}} \\ {\text{subtract 3 positives}} &{\text{subtract 3 negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}}\end{array}\nonumber\]
- Subtraction Property: Subtracting a number is the same as adding its opposite.
Glossary
- absolute value
- The absolute value of a number is its distance from 0 on the number line. The absolute value of a number nn is written as |n|.
- integers
- The whole numbers and their opposites are called the integers: \(...−3, −2, −1, 0, 1, 2, 3...\)
- opposite
- The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero: −\(a\) means the opposite of the number. The notation −\(a\) is read “the opposite of \(a\).”


