2.7: Solve Compound Inequalities
- Page ID
- 17390
By the end of this section, you will be able to:
- Solve compound inequalities with “and”
- Solve compound inequalities with “or”
- Solve applications with compound inequalities
Before you get started, take this readiness quiz.
Solve Compound Inequalities with “and”
Now that we know how to solve linear inequalities, the next step is to look at compound inequalities. A compound inequality is made up of two inequalities connected by the word “and” or the word “or.” For example, the following are compound inequalities.
\[\begin{array} {lll} {x+3>−4} &{\text{and}} &{4x−5\leq 3} \\ {2(y+1)<0} &{\text{or}} &{y−5\geq −2} \\ \end{array} \nonumber\]
A compound inequality is made up of two inequalities connected by the word “and” or the word “or.”
To solve a compound inequality means to find all values of the variable that make the compound inequality a true statement. We solve compound inequalities using the same techniques we used to solve linear inequalities. We solve each inequality separately and then consider the two solutions.
To solve a compound inequality with the word “and,” we look for all numbers that make both inequalities true. To solve a compound inequality with the word “or,” we look for all numbers that make either inequality true.
Let’s start with the compound inequalities with “and.” Our solution will be the numbers that are solutions to both inequalities known as the intersection of the two inequalities. Consider the intersection of two streets—the part where the streets overlap—belongs to both streets.
To find the solution of an "and" compound inequality, we look at the graphs of each inequality and then find the numbers that belong to both graphs—where the graphs overlap.
For the compound inequality \(x>−3\) and \(x\leq 2\), we graph each inequality. We then look for where the graphs “overlap”. The numbers that are shaded on both graphs, will be shaded on the graph of the solution of the compound inequality. See Figure \(\PageIndex{1}\).
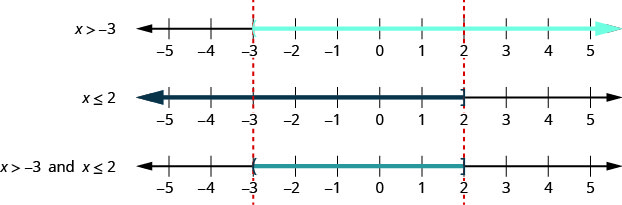
We can see that the numbers between \(−3\) and \(2\) are shaded on both of the first two graphs. They will then be shaded on the solution graph.
The number \(−3\) is not shaded on the first graph and so since it is not shaded on both graphs, it is not included on the solution graph.
The number two is shaded on both the first and second graphs. Therefore, it is be shaded on the solution graph.
This is how we will show our solution in the next examples.
Solve \(6x−3<9\) and \(2x+7\geq 3\). Graph the solution and write the solution in interval notation.
Solution
| \(6x−3<9\) | and | \(2x+9\geq 3\) | |
| Step 1. Solve each inequality. |
\(6x−3<9\) | \(2x+9\geq 3\) | |
| \(6x<12\) | \(2x\geq −6\) | ||
| \(x<2\) | and | \(x\geq −3\) | |
| Step 2. Graph each solution. Then graph the numbers that make both inequalities true. The final graph will show all the numbers that make both inequalities true—the numbers shaded on both of the first two graphs. | 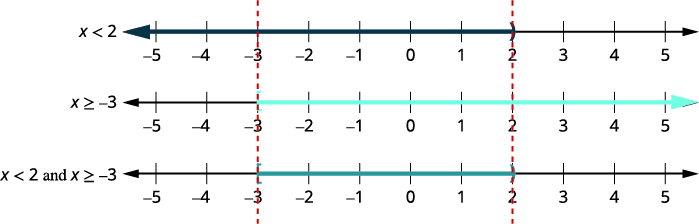 |
||
| Step 3. Write the solution in interval notation. | \([−3,2)\) | ||
| All the numbers that make both inequalities true are the solution to the compound inequality. | |||
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(4x−7<9\) and \(5x+8\geq 3\).
- Answer
-
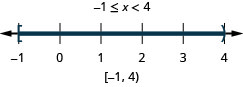
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(3x−4<5\) and \(4x+9\geq 1\).
- Answer
-
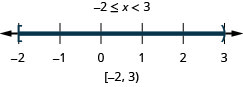
- Solve each inequality.
- Graph each solution. Then graph the numbers that make both inequalities true.
This graph shows the solution to the compound inequality. - Write the solution in interval notation.
Solve \(3(2x+5)\leq 18\) and \(2(x−7)<−6\). Graph the solution and write the solution in interval notation.
Solution
| \(3(2x+5)\leq 18\) | and | \(2(x−7)<−6\) | |
| Solve each inequality. |
\(6x+15\leq 18\) | \(2x−14<−6\) | |
| \(6x\leq 3\) | \(2x<8\) | ||
| \(x\leq \frac{1}{2}\) | and | \(x<4\) | |
| Graph each solution. |
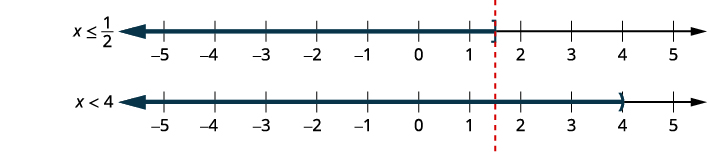 |
||
| Graph the numbers that make both inequalities true. |
 |
||
| Write the solution in interval notation. |
\((−\infty, \frac{1}{2}]\) | ||
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(2(3x+1)\leq 20\) and \(4(x−1)<2\).
- Answer
-
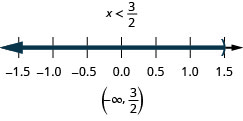
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(5(3x−1)\leq 10\) and \(4(x+3)<8\).
- Answer
-
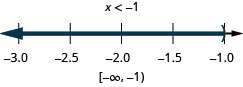
Solve \(\frac{1}{3}x−4\geq −2\) and \(−2(x−3)\geq 4\). Graph the solution and write the solution in interval notation.
Solution
| \(\frac{1}{3}x−4\geq −2\) | and | \(−2(x−3)\geq 4\) | |
| Solve each inequality. | \(\frac{1}{3}x−4\geq −2\) | \(−2x+6\geq 4\) | |
| \(\frac{1}{3}x\geq 2\) | \(−2x\geq −2\) | ||
| \(x\geq 6\) | and | \(x\leq 1\) | |
| Graph each solution. |  |
||
| Graph the numbers that make both inequalities true. |
 |
||
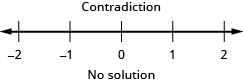
| This is a contradiction. There are no numbers that make both inequalities true, so there is no solution. | |||
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(\frac{1}{4}x−3\geq −1\) and \(−3(x−2)\geq 2\).
- Answer
-
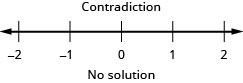
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(\frac{1}{5}x−5\geq −3\) and \(−4(x−1)\geq −2\).
- Answer
-
Sometimes we have a compound inequality that can be written more concisely. For example, \(a<x\) and \(x<b\) can be written simply as \(a<x<b\) and then we call it a double inequality. The two forms are equivalent.
A double inequality is a compound inequality such as \(a<x<b\). It is equivalent to \(a<x\) and \(x<b\).
\[\text{Other forms:} \quad \begin{array} {lllll} {a<x<b} &{\text{is equivalent to }} &{a<x} &{\text{and}} &{x<b} \\ {a\leq x\leq b} &{\text{is equivalent to }} &{a\leq x} &{\text{and}} &{x\leq b} \\ {a>x>b} &{\text{is equivalent to }} &{a>x} &{\text{and}} &{x>b} \\ {a\geq x\geq b} &{\text{is equivalent to }} &{a\geq x} &{\text{and}} &{x\geq b} \\ \end{array} \nonumber\]
To solve a double inequality we perform the same operation on all three “parts” of the double inequality with the goal of isolating the variable in the center.
Solve \(−4\leq 3x−7<8\). Graph the solution and write the solution in interval notation.
Solution
| \(-4 \leq 3x - 7 < 8\) | |
| Add 7 to all three parts. | \( -4 \,{\color{red}{+\, 7}} \leq 3x - 7 \,{\color{red}{+ \,7}} < 8 \,{\color{red}{+ \,7}}\) |
| Simplify. | \( 3 \le 3x < 15 \) |
| Divide each part by three. | \( \dfrac{3}{\color{red}{3}} \leq \dfrac{3x}{\color{red}{3}} < \dfrac{15}{\color{red}{3}} \) |
| Simplify. | \( 1 \leq x < 5 \) |
| Graph the solution. |  |
| Write the solution in interval notation. | \( [1, 5) \) |
When written as a double inequality, \(1\leq x<5\), it is easy to see that the solutions are the numbers caught between one and five, including one, but not five. We can then graph the solution immediately as we did above.
Another way to graph the solution of \(1\leq x<5\) is to graph both the solution of \(x\geq 1\) and the solution of \(x<5\). We would then find the numbers that make both inequalities true as we did in previous examples.
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(−5\leq 4x−1<7\).
- Answer
-
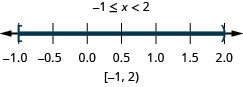
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(−3<2x−5\leq 1\).
- Answer
-
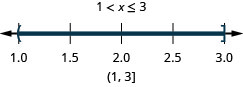
Solve Compound Inequalities with “or”
To solve a compound inequality with “or”, we start out just as we did with the compound inequalities with “and”—we solve the two inequalities. Then we find all the numbers that make either inequality true.
Just as the United States is the union of all of the 50 states, the solution will be the union of all the numbers that make either inequality true. To find the solution of the compound inequality, we look at the graphs of each inequality, find the numbers that belong to either graph and put all those numbers together.
To write the solution in interval notation, we will often use the union symbol, \(\cup\), to show the union of the solutions shown in the graphs.
- Solve each inequality.
- Graph each solution. Then graph the numbers that make either inequality true.
- Write the solution in interval notation.
Solve \(5−3x\leq −1\) or \(8+2x\leq 5\). Graph the solution and write the solution in interval notation.
Solution
| \(5−3x\leq −1\) | or | \(8+2x\leq 5\) | |
| Solve each inequality. | \(5−3x\leq −1\) | \(8+2x\leq 5\) | |
| \(−3x\leq −6\) | \(2x\leq −3\) | ||
| \(x\geq 2\) | or | \(x\leq −\frac{3}{2}\) | |
| Graph each solution. | 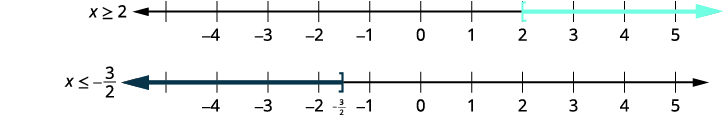 |
||
| Graph numbers that make either inequality true. |
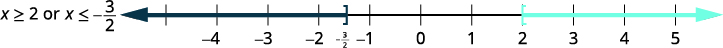 |
||
| \((−\infty,−\frac{3}{2}]\cup[2,\infty)\) | |||
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(1−2x\leq −3\) or \(7+3x\leq 4\).
- Answer
-
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(2−5x\leq −3\) or \(5+2x\leq 3\).
- Answer
-
Solve \(\frac{2}{3}x−4\leq 3\) or \(\frac{1}{4}(x+8)\geq −1\). Graph the solution and write the solution in interval notation.
Solution
| \(\frac{2}{3}x−4\leq 3\) | or | \(\frac{1}{4}(x+8)\geq −1\) | |
| Solve each inequality. |
\(3(\frac{2}{3}x−4)\leq 3(3)\) | \(4⋅\frac{1}{4}(x+8)\geq 4⋅(−1)\) | |
| \(2x−12\leq 9\) | \(x+8\geq −4\) | ||
| \(2x\leq 21\) | \(x\geq −12\) | ||
| \(x\leq \frac{21}{2}\) | |||
| \(x\leq \frac{21}{2}\) | or | \(x\geq −12\) | |
| Graph each solution. |
 |
||
| Graph numbers that make either inequality true. |
 |
||
| The solution covers all real numbers. | |||
| \((−\infty ,\infty )\) | |||
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(\frac{3}{5}x−7\leq −1\) or \(\frac{1}{3}(x+6)\geq −2\).
- Answer
-
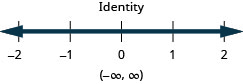
Solve the compound inequality. Graph the solution and write the solution in interval notation: \(\frac{3}{4}x−3\leq 3\) or \(\frac{2}{5}(x+10)\geq 0\).
- Answer
-
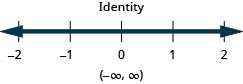
Solve Applications with Compound Inequalities
Situations in the real world also involve compound inequalities. We will use the same problem solving strategy that we used to solve linear equation and inequality applications.
Recall the problem solving strategies are to first read the problem and make sure all the words are understood. Then, identify what we are looking for and assign a variable to represent it. Next, restate the problem in one sentence to make it easy to translate into a compound inequality. Last, we will solve the compound inequality.
Due to the drought in California, many communities have tiered water rates. There are different rates for Conservation Usage, Normal Usage and Excessive Usage. The usage is measured in the number of hundred cubic feet (hcf) the property owner uses.
During the summer, a property owner will pay $24.72 plus $1.54 per hcf for Normal Usage. The bill for Normal Usage would be between or equal to $57.06 and $171.02. How many hcf can the owner use if he wants his usage to stay in the normal range?
Solution
| Identify what we are looking for. | The number of hcf he can use and stay in the “normal usage” billing range. |
| Name what we are looking for. | Let x= the number of hcf he can use. |
| Translate to an inequality. | Bill is $24.72 plus $1.54 times the number of hcf he uses or \(24.72+1.54x\). |
|
\(\color{Cerulean}{\underbrace{\color{black}{\text{His bill will be between or equal to }$57.06\text{ and }$171.02.}}}\) \(57.06 \leq 24.72 + 1.54x \leq 171.02 \) |
|
| Solve the inequality. |
\(57.06 \leq 24.72 + 1.54x \leq 171.02\) \(57.06 \,{\color{red}{- \,24.72}}\leq 24.72 \,{\color{red}{- \,24.72}} + 1.54x \leq 171.02 \,{\color{red}{- \,24.72}}\) \( 32.34 \leq 1.54x \leq 146.3\) \( \dfrac{32.34}{\color{red}{1.54}} \leq \dfrac{1.54x}{\color{red}{1.54}} \leq \dfrac{146.3}{\color{red}{1.54}}\) \( 21 \leq x \leq 95 \) |
| Answer the question. | The property owner can use \(21–95\) hcf and still fall within the “normal usage” billing range. |
Due to the drought in California, many communities now have tiered water rates. There are different rates for Conservation Usage, Normal Usage and Excessive Usage. The usage is measured in the number of hundred cubic feet (hcf) the property owner uses.
During the summer, a property owner will pay $24.72 plus $1.32 per hcf for Conservation Usage. The bill for Conservation Usage would be between or equal to $31.32 and $51.12. How many hcf can the owner use if she wants her usage to stay in the conservation range?
- Answer
-
The homeowner can use \(5–20\) hcf and still fall within the “conservation usage” billing range.
Due to the drought in California, many communities have tiered water rates. There are different rates for Conservation Usage, Normal Usage and Excessive Usage. The usage is measured in the number of hundred cubic feet (hcf) the property owner uses.
During the winter, a property owner will pay $24.72 plus $1.54 per hcf for Normal Usage. The bill for Normal Usage would be between or equal to $49.36 and $86.32. How many hcf will he be allowed to use if he wants his usage to stay in the normal range?
- Answer
-
The homeowner can use \(16–40\) hcf and still fall within the “normal usage” billing range.
Access this online resource for additional instruction and practice with solving compound inequalities.
- Compound inequalities
Key Concepts
- How to solve a compound inequality with “and”
- Solve each inequality.
- Graph each solution. Then graph the numbers that make both inequalities true. This graph shows the solution to the compound inequality.
- Write the solution in interval notation.
- Double Inequality
- A double inequality is a compound inequality such as \(a<x<b\). It is equivalent to \(a<x\) and \(x<b.\)
Other forms: \[\begin{align*} a<x<b & & \text{is equivalent to} & & a<x\;\text{and}\;x<b \\
a≤x≤b & & \text{is equivalent to} & & a≤x\;\text{and}\;x≤b \\
a>x>b & & \text{is equivalent to} & & a>x\;\text{and}\;x>b \\
a≥x≥b & & \text{is equivalent to} & & a≥x\;\text{and}\;x≥b \end{align*}\]
- A double inequality is a compound inequality such as \(a<x<b\). It is equivalent to \(a<x\) and \(x<b.\)
- How to solve a compound inequality with “or”
- Solve each inequality.
- Graph each solution. Then graph the numbers that make either inequality true.
- Write the solution in interval notation.
Glossary
- compound inequality
- A compound inequality is made up of two inequalities connected by the word “and” or the word “or.”


