6.1: The Greatest Common Factor

Last updated
Save as PDF

Page ID: 19884

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

We begin this section with deﬁnitions of factors and divisors. Because $24 = 2\cdot 12$, both $2$ and $12$ are factors of $24$. However, note that $2$ is also a divisor of $24$, because when you divide $24$ by $2$ you get $12$, with a remainder of zero. Similarly, $12$ is also a divisor of $24$, because when you divide $24$ by $12$ you get $2$, with a remainder of zero.

Definitions: Factors and Divisors

Suppose $m$ and $n$ are integers. Then $m$ is a divisor (factor) of $n$ if and only if there exists another integer $k$ so that $n=m \cdot k$.

The words divisor and factor are equivalent. They have the same meaning.

Example $\PageIndex{1}$

List the positive divisors (factors) of $24$.

Solution

First, list all possible ways that we can express $24$ as a product of two positive integers:

\[24=1 \cdot 24 \quad \text { or } \quad 24=2 \cdot 12 \quad \text { or } \quad 24=3 \cdot 8 \quad \text { or } \quad 24=4 \cdot 6 \nonumber \]

Therefore, the positive divisors (factors) of $24$ are $1,2,3,4,6,8,$ and $24$.

Exercise $\PageIndex{1}$

List the positive divisors of $18$.

Answer: $1,2,3,6,9,$ and $18$

Example $\PageIndex{2}$

List the positive divisors (factors) that $36$ and $48$ have in common.

Solution

First, list all positive divisors (factors) of $36$ and $48$ separately, then box the divisors that are in common.

Divisors of $36$ are: $[1],[2],[3],[4],[6], 9, [12], 18, 36$

Divisors of $48$ are: $[1],[2],[3],[4],[6], 8, [12], 16, 24, 48$

Therefore, the common positive divisors (factors) of $36$ and $48$ are $1, 2, 3, 4, 6,$ and $12$.

Exercise $\PageIndex{2}$

List the positive divisors that $40$ and $60$ have in common.

Answer: $1,2,4,5,10,$ and $20$

Definition: Greatest Common Divisor

The greatest common divisor (factor) of $a$ and $b$ is the largest positive number that divides evenly (no remainder) both $a$ and $b$. The greatest common divisor of $a$ and $b$ is denoted by the symbolism $\operatorname{GCD}(a, b)$. We will also use the abbreviation $\operatorname{GCF}(a, b)$ to represents the greatest common factor of $a$ and $b$.

Remember, greatest common divisor and greatest common factor have the same meaning. In Example $\PageIndex{2}$, we listed the common positive divisors of $36$ and $48$. The largest of these common divisors was $12$. Hence, the greatest common divisor (factor) of $36$ and $48$ is $12$, written $\operatorname{GCD}(36, 48)=12$.

With smaller numbers, it is usually easy to identify the greatest common divisor (factor).

Example $\PageIndex{3}$

State the greatest common divisor (factor) of each of the following pairs of numbers:

$18$ and $24$
$30$ and $40$
$16$ and $24$

Solution

In each case, we must ﬁnd the largest possible positive integer that divides evenly into both the given numbers.

The largest positive integer that divides evenly into both $18$ and $24$ is $6$. Thus, $\operatorname{GCD}(18, 24)=6$.
The largest positive integer that divides evenly into both $30$ and $40$ is $10$. Thus, $\operatorname{GCD}(30, 40)=10$.
The largest positive integer that divides evenly into both $16$ and $24$ is $8$. Thus, $\operatorname{GCD}(16, 24)=8$.

Exercise $\PageIndex{3}$

State the greatest common divisor of $36$ and $60$.

Answer: $12$

With larger numbers, it is harder to identify the greatest common divisor (factor). However, prime factorization will save the day!

Example $\PageIndex{4}$

Find the greatest common divisor (factor) of $360$ and $756$.

Solution

Prime factor $360$ and $756$, writing your answer in exponential form.

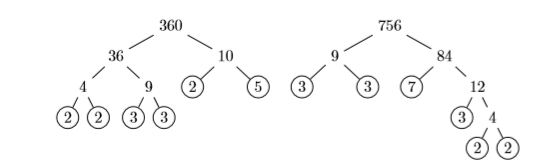
Thus:

\[\begin{array}{l}{360=2^{3} \cdot 3^{2} \cdot 5} \\ {756=2^{2} \cdot 3^{3} \cdot 7}\end{array} \nonumber \]

Note

To ﬁnd the greatest common divisor (factor), list each factor that appears in common to the highest power that appears in common.

In this case, the factors $2$ and $3$ appear in common, with $22$ being the highest power of $2$ and $32$ being the highest power of $3$ that appear in common. Therefore, the greatest common divisor of $360$ and $756$ is:

\[\begin{aligned} \mathrm{GCD}(360,756) &=2^{2} \cdot 3^{2} \\ &=4 \cdot 9 \\ &=36 \end{aligned} \nonumber \]

Therefore, the greatest common divisor (factor) is $\mathrm{GCD}(360,756)=36$. Note what happens when we write each of the given numbers as a product of the greatest common factor and a second factor:

\[\begin{array}{l}{360={\color {Red} 36} \cdot 10} \\ {756={\color {Red} 36} \cdot 21}\end{array} \nonumber \]

In each case, note how the second second factors ($10$ and $21$) contain no additional common factors.

Exercise $\PageIndex{4}$

Find the greatest common divisor of $120$ and $450$.

Answer: $30$

Finding the Greatest Common Factor of Monomials

Example $\PageIndex{4}$ reveals the technique used to ﬁnd the greatest common factor of two or more monomials.

Finding the GCF of two or more monomials

To ﬁnd the greatest common factor of two or more monomials, proceed as follows:

Find the greatest common factor (divisor) of the coeﬃcients of the given monomials. Use prime factorization if necessary.
List each variable that appears in common in the given monomials.
Raise each variable that appears in common to the highest power that appears in common among the given monomials.

Example $\PageIndex{5}$

Find the greatest common factor of $6 x^{3} y^{3}$ and $9 x^{2} y^{5}$.

Solution

To ﬁnd the $\mathrm{GCF}$ of $6 x^{3} y^{3}$ and $9 x^{2} y^{5}$, we note that:

The greatest common factor (divisor) of $6$ and $9$ is $3$.
The monomials $6x^3y^3$ and $9x^2y^5$ have the variables $x$ and $y$ in common.
The highest power of $x$ in common is $x^2$. The highest power of $y$ in common is $y^3$.

Thus, the greatest common factor is $\mathrm{GCF}\left(6 x^{3} y^{3}, 9 x^{2} y^{5}\right)=3 x^{2} y^{3}$. Note what happens when we write each of the given monomials as a product of the greatest common factor and a second monomial:

\[\begin{array}{l}{6 x^{3} y^{3}={\color {Red} 3 x^{2} y^{3}} \cdot 2 x} \\ {9 x^{2} y^{5}={\color {Red} 3 x^{2} y^{3}} \cdot 3 y}\end{array} \nonumber \]

Observe that the set of second monomial factors ($2x$ and $3y$) contain no additional common factors.

Exercise $\PageIndex{5}$

Find the greatest common factor of $16xy^3$ and $12x^4y^2$.

Answer: $4 x y^{2}$

Example $\PageIndex{6}$

Find the greatest common factor of $12x^4$, $18 x^3$, and $30 x^2$.

Solution

To ﬁnd the $\mathrm{GCF}$ of $12x^4$, $18 x^3$, and $30 x^2$, we note that:

The greatest common factor (divisor) of $12$, $18$, and $30$ is $6$.
The monomials $12x^4$, $18 x^3$, and $30 x^2$ have the variable $x$ in common.
The highest power of $x$ in common is $x^2$.

Thus, the greatest common factor is $\mathrm{GCF}\left(12 x^{4}, 18 x^{3}, 30 x^{2}\right)=6 x^{2}$. Note what happens when we write each of the given monomials as a product of the greatest common factor and a second monomial:

\[\begin{array}{l}{12 x^{4}={\color {Red}6 x^{2}} \cdot 2 x^{2}} \\ {18 x^{3}={\color {Red}6 x^{2}} \cdot 3 x} \\ {30 x^{2}={\color {Red}6 x^{2}} \cdot 5}\end{array} \nonumber \]

Observe that the set of second monomial factors ($2x^2$, $3 x$, and $5$) contain no additional common factors.

Exercise $\PageIndex{6}$

Find the greatest common factor of $6y^3$, $15 y^2$, and $9 y^5$.

Answer: $3 y^{2}$

Factor Out the GCF

In Chapter 5, we multiplied a monomial and polynomial by distributing the monomial times each term in the polynomial.

\[\begin{aligned} {\color {Red}2 x(}3 x^{2}+4 x-7{\color {Red})} &={\color {Red}2 x} \cdot 3 x^{2}+{\color {Red}2 x} \cdot 4 x-{\color {Red}2 x} \cdot 7 \\ &=6 x^{3}+8 x^{2}-14 x \end{aligned} \nonumber \]

In this section we reverse that multiplication process. We present you with the ﬁnal product and ask you to bring back the original multiplication problem. In the case $6 x^{3}+8 x^{2}-14 x$, the greatest common factor of $6x^3$, $8x^2$, and $14x$ is $2x$. We then use the distributive property to factor out $2x$ from each term of the polynomial.

\[\begin{aligned} 6 x^{3}+8 x^{2}-14 x &={\color {Red}2 x} \cdot 3 x^{2}+{\color {Red}2 x} \cdot 4 x-{\color {Red}2 x} \cdot 7 \\ &={\color {Red}2 x(}3 x^{2}+4 x-7{\color {Red})} \end{aligned} \nonumber \]

Factoring

Factoring is “unmultiplying.” You are given the product, then asked to ﬁnd the original multiplication problem.

First rule of factoring

If the terms of the given polynomial have a greatest common factor ($\mathrm{GCF}$), then factor out the $\mathrm{GCF}$.

Let’s look at a few examples that factor out the $\mathrm{GCF}$.

Example $\PageIndex{7}$

Factor: $6 x^{2}+10 x+14$

Solution

The greatest common factor ($\mathrm{GCF}$) of $6x^2$, $10 x$ and $14$ is $2$. Factor out the $\mathrm{GCF}$.

\[\begin{aligned} 6 x^{2}+10x+14 x &={\color {Red}2 } \cdot 3 x^{2}+{\color {Red}2 } \cdot 5 x+{\color {Red}2 } \cdot 7 \\ &={\color {Red}2 (}3 x^{2}+5 x+7{\color {Red})} \end{aligned} \nonumber \]

Checking your work

Every time you factor a polynomial, remultiply to check your work.

Check: Multiply. Distribute the $2$.

\[\begin{aligned} {\color {Red}2 (}3 x^{2}+5 x+7{\color {Red})} &={\color {Red}2 } \cdot 3 x^{2}+{\color {Red}2 } \cdot 5 x+{\color {Red}2 } \cdot 7 \\ &=6 x^{2}+10 x+14 \end{aligned} \nonumber \]

That’s the original polynomial, so we factored correctly.

Exercise $\PageIndex{7}$

Factor: $9 y^{2}-15 y+12$

Answer: $3\left(3 y^{2}-5 y+4\right)$

Example $\PageIndex{8}$

Factor: $12 y^{5}-32 y^{4}+8 y^{2}$

Solution

The greatest common factor ($\mathrm{GCF}$) of $12y^5$, $32y^4$ and $8y^2$ is $4y^2$. Factor out the $\mathrm{GCF}$.

\[\begin{aligned} 12 y^{5}-32 y^{4}+8 y^{2} &={\color {Red}4 y^{2}} \cdot 3 y^{3}-{\color {Red}4 y^{2}} \cdot 8 y^{2}+{\color {Red}4 y^{2}} \cdot 2 \\ &={\color {Red}4 y^{2} (}3 y^{3}-8 y^{2}+2{\color {Red})} \end{aligned} \nonumber \]

Check: Multiply. Distribute the monomial $4y^2$.

\[\begin{aligned} {\color {Red}4 y^{2} (}3 y^{3}-8 y^{2}+2{\color {Red})} &={\color {Red}4 y^{2}} \cdot 3 y^{3}-{\color {Red}4 y^{2}} \cdot 8 y^{2}+{\color {Red}4 y^{2}} \cdot 2 \\ &=12 y^{5}-32 y^{4}+8 y^{2} \end{aligned} \nonumber \]

That’s the original polynomial. We have factored correctly.

Exercise $\PageIndex{8}$

Factor: $8 x^{6}+20 x^{4}-24 x^{3}$

Answer: $4 x^{3}\left(2 x^{3}+5 x-6\right)$

Example $\PageIndex{9}$

Factor: $12 a^{3} b+24 a^{2} b^{2}+12 a b^{3}$

Solution

The greatest common factor ($\mathrm{GCF}$) of $12a^3b$, $24 a^2b^2$ and $12ab^3$ is $12ab$. Factor out the $\mathrm{GCF}$.

\[\begin{aligned} 12 a^{3} b+24 a^{2} b^{2}+12 a b^{3} &={\color {Red}12ab} \cdot a^{2}-{\color {Red}12ab} \cdot 2 a b+{\color {Red}12ab} \cdot b^{2} \\ &= {\color {Red}12ab (}a^{2}+2ab+b^{2}{\color {Red})} \end{aligned} \nonumber \]

Check: Multiply. Distribute the monomial $12ab$.

\[\begin{aligned} {\color {Red}12ab (}a^{2}+2ab+b^{2}{\color {Red})} &={\color {Red}12ab} \cdot a^{2}-{\color {Red}12ab} \cdot 2 a b+{\color {Red}12ab} \cdot b^{2} \\ &=12 a^{3} b+24 a^{2} b^{2}+12 a b^{3} \end{aligned} \nonumber \]

That’s the original polynomial. We have factored correctly.

Exercise $\PageIndex{9}$

Factor: $15 s^{2} t^{4}+6 s^{3} t^{2}+9 s^{2} t^{2}$

Answer: $3 s^{2} t^{2}\left(5 t^{2}+2 s+3\right)$

Speeding Things Up a Bit

Eventually, after showing your work on a number of examples such as those in Examples $\PageIndex{7}$, $\PageIndex{8}$, and $\PageIndex{9}$, you’ll need to learn how to perform the process mentally.

Example $\PageIndex{10}$

Factor each of the following polynomials:

$24 x+32$
$5 x^{3}-10 x^{2}-10 x$
$2 x^{4} y+2 x^{3} y^{2}-6 x^{2} y^{3}$

Solution

In each case, factor out the greatest common factor ($\mathrm{GCF}$):

The $\mathrm{GCF}$ of $24x$ and $32$ is $8$. Thus,\[24x + 32 = 8(3x + 4) \nonumber \]
The $\mathrm{GCF}$ of $5x^3$, $10 x^2$, and $10 x$ is $5x$. Thus: \[5 x^{3}-10 x^{2}-10 x=5 x\left(x^{2}-2 x-2\right) \nonumber \]
The $\mathrm{GCF}$ of $2x^4y$, $2x^3y^2$, and $6x^2y^3$ is $2x^2y$. Thus:\[2 x^{4} y+2 x^{3} y^{2}-6 x^{2} y^{3}=2 x^{2} y\left(x^{2}+x y-3 y^{2}\right) \nonumber \]

As you speed things up by mentally factoring out the $\mathrm{GCF}$, it is even more important that you check your results. The check can also be done mentally. For example, in checking the third result, mentally distribute $2x^2y$ times each term of $x^2 +xy−3y^2$. Multiplying $2x^2y$ times the ﬁrst term $x^2$ produces $2x^4y$, the ﬁrst term in the original polynomial.

$fig 6.1.a.png$

Continue in this manner, mentally checking the product of $2x^2y$ with each term of $x^2 + xy −3y^2$, making sure that each result agrees with the corresponding term of the original polynomial.

Exercise $\PageIndex{10}$

Factor: $18 p^{5} q^{4}-30 p^{4} q^{5}+42 p^{3} q^{6}$

Answer: $6 p^{3} q^{4}\left(3 p^{2}-5 p q+7 q^{2}\right)$

Remember that the distributive property allows us to pull the $\mathrm{GCF}$ out in front of the expression or to pull it out in back. In symbols:

${\color {Red}a}b+{\color {Red}a}c={\color {Red}a}(b+c) \quad$ or $\quad b{\color {Red}a}+c{\color {Red}a}=(b+c){\color {Red}a}$

Example $\PageIndex{11}$

Factor: $2 x(3 x+2)+5(3 x+2)$

Solution

In this case, the greatest common factor ($\mathrm{GCF}$) is $3x + 2$.

\[\begin{aligned} 2x(3 x+2)+5(3 x+2) &=2x \cdot {\color {Red}(3 x+2)}+5 \cdot{\color {Red}(3 x+2)} \\ &=(2 x+5){\color {Red}(3 x+2)} \end{aligned} \nonumber \]

Because of the commutative property of multiplication, it is equally valid to pull the $\mathrm{GCF}$ out in front.

\[\begin{aligned} 2x(3 x+2)+5(3 x+2) &=2x \cdot {\color {Red}(3 x+2)}+5 \cdot{\color {Red}(3 x+2)} \\ &={\color {Red}(3 x+2)} (2 x+5)\end{aligned}\]

Note that the order of factors diﬀers from the ﬁrst solution, but because of the commutative property of multiplication, the order does not matter. The answers are the same.

Exercise $\PageIndex{11}$

Factor: $3 x^{2}(4 x-7)+8(4 x-7)$

Answer: $\left(3 x^{2}+8\right)(4 x-7)$

Example $\PageIndex{12}$

Factor: $15 a(a+b)-12(a+b)$

Solution

In this case, the greatest common factor ($\mathrm{GCF}$) is $3(a + b)$.

\[\begin{aligned} 15 a(a+b)-12(a+b) &={\color {Red}3(a+b)} \cdot 5 a-{\color {Red}3(a+b)} \cdot 4 \\ &={\color {Red}3(a+b)}(5 a-4) \end{aligned} \nonumber \]

Alternate solution:

It is possible that you might fail to notice that $15$ and $12$ are divisible by $3$, factoring out only the common factor $a + b$.

\[\begin{aligned} 15 a(a+b)-12(a+b) &=15a\cdot {\color {Red}(a+b)} - 12\cdot {\color {Red}(a+b)} \\ &=(15a-12) {\color {Red}(a+b)}\end{aligned} \nonumber \]

However, you now need to notice that you can continue, factoring out $3$ from both $15a$ and $12$.

$=3(5 a-4)(a+b)$

Note that the order of factors diﬀers from the ﬁrst solution, but because of the commutative property of multiplication, the order does not matter. The answers are the same.

Exercise $\PageIndex{12}$

Factor: $24 m(m-2 n)+20(m-2 n)$

Answer: $4(6 m+5)(m-2 n)$

Factoring by Grouping

The ﬁnal factoring skill in this section involves four-term expressions. The technique for factoring a four-term expression is called factoring by grouping.

Example $\PageIndex{13}$

Factor by grouping: $x^{2}+8 x+3 x+24$

Solution

We “group” the ﬁrst and second terms, noting that we can factor an $x$ out of both of these terms. Then we “group” the third and fourth terms, noting that we can factor $3$ out of both of these terms.

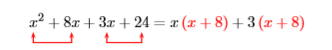
$fig 6.1.b.png$

Now we can factor $x + 8$ out of both of these terms.

$(x+3){\color {Red}(x+8)}$

Exercise $\PageIndex{13}$

Factor by grouping: $x^{2}-6 x+2 x-12$

Answer: $(x+2)(x-6)$

Let’s try a grouping that contains some negative signs.

Example $\PageIndex{14}$

Factor by grouping: $x^{2}+4 x-7 x-28$

Solution

We “group” the ﬁrst and second terms, noting that we can factor $x$ out of both of these terms. Then we “group” the third and fourth terms, then try to factor a $7$ out of both these terms.

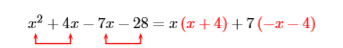
$fig 6.1.c.png$

This does not lead to a common factor. Let’s try again, this time factoring a $−7$ out of the third and fourth terms.

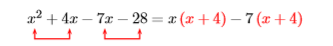
$fig 6.1.d.png$

That worked! We now factor out a common factor $x + 4$.

$(x-7){\color {Red}(x+4)}$

Exercise $\PageIndex{14}$

Factor by grouping: $x^{2}-5 x-4 x+20$

Answer: $(x-4)(x-5)$

Let’s increase the size of the numbers a bit.

Example $\PageIndex{15}$

Factor by grouping: $6 x^{2}-8 x+9 x-12$

Solution

Note that we can factor $2x$ out of the ﬁrst two terms and $3$ out of the second two terms.

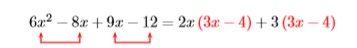
$fig 6.1.e.png$

Now we have a common factor $3x−4$ which we can factor out.

$(2x+3){\color {Red}(3x-4)}$

Exercise $\PageIndex{15}$

Factor by grouping: $15 x^{2}+9 x+10 x+6$

Answer: $(3 x+2)(5 x+3)$

As the numbers get larger and larger, you need to factor out the ($\mathrm{GCF}$) from each grouping. If not, you won’t get a common factor to ﬁnish the factoring.

Example $\PageIndex{16}$

Factor by grouping: $24 x^{2}-32 x-45 x+60$

Solution

Suppose that we factor $8x$ out of the ﬁrst two terms and $−5$ out of the second two terms.

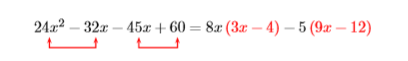
$fig 6.1.f.png$

That did not work, as we don’t have a common factor to complete the factoring process. However, note that we can still factor out a $3$ from $9x−12$. As we’ve already factored out a $5$, and now we see can factor out an additional $3$, this means that we should have factored out $3$ times $5$, or $15$, to begin with. Let’s start again, only this time we’ll factor $15$ out of the second two terms.

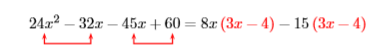
$fig 6.1.g.png$

Beautiful! We can now factor out $3x−4$.

$(8x-15){\color {Red}(3x-4)}$

Exercise $\PageIndex{16}$

Factor by grouping: $36 x^{2}-84 x+15 x-35$

Answer: $(12 x+5)(3 x-7)$