1.2: Factoring
- Page ID
- 40890
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This section will review three of the most common types of factoring - factoring out a Greatest Common Factor, Trinomial Factoring and factoring a Difference of Squares.
Greatest Common Factor
Factoring out a greatest common factor essentially undoes the distributive multiplication that often occurs in mathematical expressions. This factor may be monomial or polynomial, but in these examples, we will explore monomial common factors.
In multiplying \(3 x y^{2}(5 x-2 y)=15 x^{2} y^{2}-6 x y^{3}\) the monomial term \(3 x y^{2}\) is multiplied or distributed to both terms inside the parentheses. The process of factorization undoes this multiplication.
Example \(\PageIndex{1}\)
Factor
\[7 x^{2}+14 x \nonumber\]
Solution
This expression has two terms. The coefficients share a common factor of 7 and the only variable involved in this expression is \(x\). The highest power of the variable that is shared by both terms is \(x^{1},\) so this is the power of \(x\) that can be factored out of both terms. The greatest common factor is \(7 x\)
\[7 x^{2}+14 x=7 x(x+2) \nonumber\]
It isn't necessary to find the greatest common factor right away. In more complicated problems, the factoring can be accomplished in pieces, similar in fashion to reducing fractions.
Example \(\PageIndex{2}\)
Factor
\[42 x^{2} y^{6}+98 x y^{3}-210 x^{3} y^{2} \nonumber\]
Solution
This expression has three terms. It's not immediately clear what the greatest common factor of the coefficients is, but they're all even numbers, so we could at least divide them all by \(2 .\) The \(98 x y^{3}\) term has an \(x^{1},\) which means that this is the hightest power of \(x\) that we could factor out of all the terms. The \(210 x^{3} y^{2}\) has a \(y^{2},\) which is the highest power of \(y\) that can be factored out of all the terms. So we can at least proceed with these factors:
\[\begin{aligned}
42 x^{2} y^{6}+98 x y^{3}-210 x^{3} y^{2} &=2 x y^{2} * 21 x y^{4}+2 x y^{2} * 49 y-2 x y^{2} * 105 x^{2} \\
&=2 x y^{2}\left(21 x y^{4}+49 y-105 x^{2}\right)
\end{aligned}\]
Now, we didn't try very hard to find the greatest common factor in the beginning of this problem, so it's important that we continue to question whether or not there are any remaining common factors. The 21 and 49 clearly share a common factor of \(7,\) so it would make sense to see if \(105\) is divisible by \(7\) as well. If we divide \(105\) by \(7,\) we see that \(105=7^{*} 15 .\) So, we can also factor out a common factor of \(7\) from the remaining terms in the parentheses.
\[\begin{aligned}
2 x y^{2}\left(21 x y^{4}+49 y-105 x^{2}\right) &=2 x y^{2}\left(7 * 3 x y^{4}+7 * 7 y-7 * 15 x^{2}\right) \\
&=7 * 2 x y^{2}\left(3 x y^{4}+7 y-15 x^{2}\right) \\
&=14 x y^{2}\left(3 x y^{4}+7 y-15 x^{2}\right)
\end{aligned}\]
Trinomial Factoring \((a=1)\)
Trinomial factoring undoes the multiplication of two binomials, and it comes in two flavors - simple and complex. The simplest form of trinomial factoring involves a trinomial expression in the form \(a x^{2}+b x+c\) in which the value of \(a\) is 1 This makes the task of factorization simpler than if the value of \(a\) is not 1.
Example \(\PageIndex{3}\)
Factor \(x^{2}+7 x+10\)
Solution
In this example, the value of \(a\) is \(1,\) which makes this type of trinomial factoring a little less difficult that it would otherwise be. Whether or not the value of \(a\) is 1 the fundamental issue that governs this type of factoring is the \(+\) or \(-\) sign of the constant term. In this problem, the constant term is positive. That means that we need to find factors of 10 that add up to \(7 .\) This is relatively straightforward:
\[ x^{2}+7 x+10=(x+2)(x+5) \nonumber \]
A companion problem to this one is \(x^{2}-7 x+10\). Notice that, in this case, the sign of the constant term is still positive, which means that we still need factors of 10 that add up to \(7 .\) This means we still need to use 2 and \(5 .\) However, in this case, instead of the +10 being produced from a multiplication of (+2)(+5) it is the result of multiplying \((-2)(-5) .\) This is what makes the 7 in the second example negative:
\[x^{2}-7 x+10=(x-2)(x-5) \nonumber\]
Example \(\PageIndex{4}\)
Factor \(x^{2}+3 x-10\)
Solution
In this case, the sign of the constant term is negative. That means that we need to find factors of 10 that have a difference of \(3 .\) This is still 5 and 2.
\[x^{2}+3 x-10=(x-2)(x+5) \nonumber\]
The multiplication of the (-2) and the (+5) produce the (-10) and the fact that the 2 and 5 have opposite signs creates the difference that gives us \((+3) .\) A companion problem to this one is \(x^{2}-3 x-10\). In this case, the sign of the constant term is still negative, which means that we still need factors of 10 that have a difference of \(3 .\) This means we still need to use 2 and \(5 .\) However in this case, instead of the (+3) as the coefficient of the middle term, we'll need a (-3) . To do this we simply reverse the signs of the 2 and 5 from the previous problem:
\[x^{2}-3 x-10=(x+2)(x-5) \nonumber\]
Now the (+2)(-5) gives us \((-10),\) but the \(+2 x-5 x\) gives us \((-3 x)\) instead of \((+3 x)\).
Example \(\PageIndex{5}\)
Factor \(x^{2}+11 x-42\)
Solution
In this problem, the sign of the constant term is negative. That means that we need factors of 42 that have a difference of \(11 .\) A systematic exploration of all the factor pairs of 42 can help us to find the correct pair:
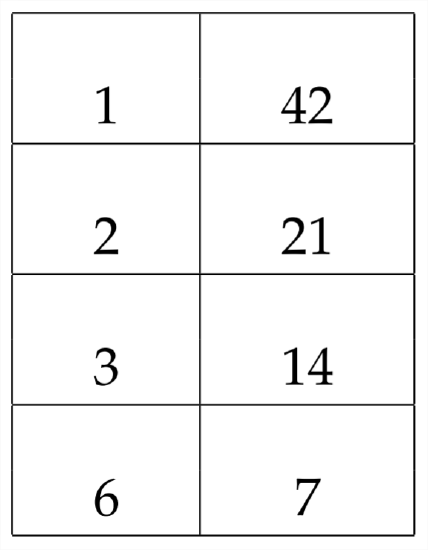
Here, we can see that the factors 3 and 14 have a difference of \(11 .\) This means that we will use these factors in our answer: \((x \quad 3)(x\)
14). In determining how to place the \(+\) and \(-\) signs in the parentheses, we can refer back to the original problem: \(x^{2}+11 x-42 .\) If we want a difference of \((+11 x),\) then we'll need to have \(a(+14)\) and \(a(-3)\)
\[x^{2}+11 x-42=(x-3)(x+14) \nonumber\]
Example \(\PageIndex{6}\)
Factor \(x^{2}+28 x+96\)
Solution
In this problem, the sign of the constant term is positive. That means that we need factors of 96 that add up to \(28 .\) A systematic exploration of all the factor pairs of 96 can help us to find the correct pair:
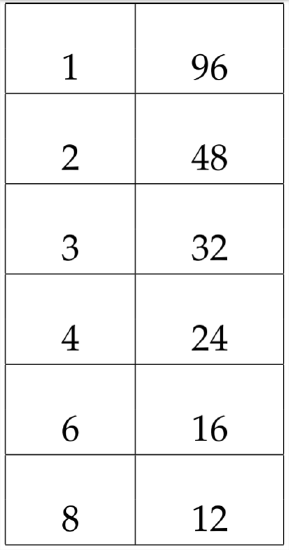
Here, we can see that the factors 4 and 24 add up to \(28 .\) This means that we will use these factors in our answer: \((x \quad 4)(x \quad 24) .\) In determining how to place the \(+\) and \(-\) signs in the parentheses, we can refer back to the original problem:
\(x^{2}+28 x+96 .\) If we want 4 and 24 to add up to \((+28),\) then they should both be positive:
\[x^{2}+28 x+96=(x+4)(x+24) \nonumber\]
In building the charts of factor pairs in the previous two problems, nothing more difficult than dividing the constant term by the numbers \(1,2,3,4,5,6, \dots\) and so on can help you to find the full list of factor pairs. If you don't get a whole number when dividing - for instance \(96 \div 5=19.2,\) then this number is not included in the list of factor pairs.
Trinomial Factoring \((a \neq 1)\)
If the value of \(a\) is not \(1,\) this means that, if the trinomial is factorable, at least one of its binomial factors also has a coefficient other than \(1 .\) For instance:
\[(2 x+7)(x-3)=2 x^{2}+1 x-21 \nonumber\]
If we were to try undo this multiplication through the process of trinomial factoring, we should look to the sign of the constant term. In this example, the sign is negative. This still means that we will need to find factor pairs that produce a difference of \((+1 x)\) as the middle term. However, in this scenario, it is not just the factors of 21 that are involved in producing the \((+1 x),\) but the combination of the factors of 21 and the factors of the leading coefficient \(2 .\) The middle term \((+1 x)\) comes from the multiplication of the \((2 x)(-3)\) and the multiplication of (+7)\((+1 x)\)
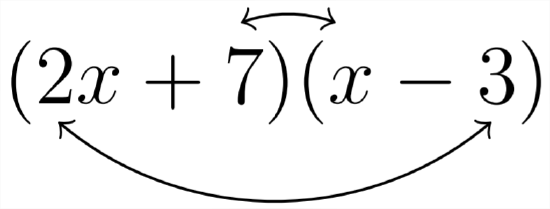
\[
\begin{aligned}
(2 x+7)(x-3) &=2 x^{2}-6 x+7 x-21 \\
&=2 x^{2}+x-21
\end{aligned}
\]
In trying to factor a trinomial like \(2 x^{2}+x-21\), we need to take this into consideration. For example, if we were to factor \(3 x^{2}-10 x+8\), we should first still look to the sign of the constant term, which, in this case, is positive. That means we want factor pairs that will add up to \(10 .\) But we have to take into consideration the interaction of the factors of the 3 with the factors of the \(8 .\) The 3 is a prime number, which means that we don't have a choice - it can only be split up into \(3 * 1,\) so we can start:
\[\text { Factor } 3 x^{2}+10 x+8\]
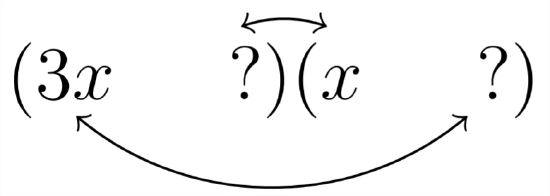
Our options for filling in the question marks will come from the factors of 8 , either \(8 * 1\) or \(4 * 2 .\) The process is by trial and error:

We can see that the choice above:
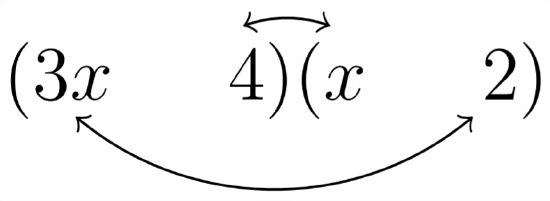
gives us the required \(10 x\) as the middle term. since the original problem was \(3 x^{2}+10 x+8\) we'll want to fill in the signs as both positive:
\[3 x^{2}+10 x+8=(3 x+4)(x+2)\]
A second method for handling this type of factoring depends on how the factors of the leading coefficient and constant term interact with each other to produce the middle term. In this process, given the problem \(3 x^{2}+10+8\), we can multiply the first and last coefficient and then look at the factor pairs of the product:
\[3 * 8=24\]
| 1 | 24 |
| 2 | 12 |
| 3 | 8 |
| 4 | 6 |
We can see that the factor pair of 24 that adds up to 10 is \(6 * 4 .\) We proceed by splitting the \(10 x\) into \(6 x+4 x\) and then factor by grouping. If you are uncomfortable with factoring by grouping, then this is probably not a good method to try. However, if you are comfortable with factoring by grouping, the rest of the process is relatively straightforward:
\[3 x^{2}+10 x+8=3 x^{2}+6 x+4 x+8\]
We then factor a common factor from the first two terms and the last two terms separately, and then factor out the common binomial factor of \((x+2)\)
\[\begin{aligned}
3 x^{2}+10 x+8 &=3 x^{2}+6 x+4 x+8 \\
&=3 x(x+2)+4(x+2) \\
&=(x+2)(3 x+4)
\end{aligned}\]
Example \(\PageIndex{7}\)
Factor \(7 x^{2}-5 x-18\)
Solution
In this example, the sign of the constant term is negative, which means that we'll need factor pairs that produce a difference of \(5 .\) The leading coefficient is \(7,\) which is prime, so, again, the only way to split up the 7 is \(7 * 1\)
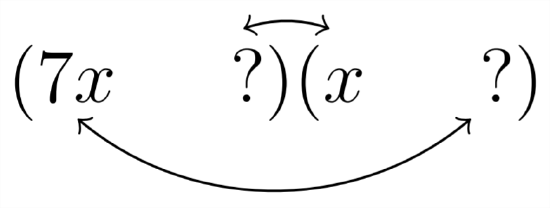
The options for filling in the question marks come from the factors of \(18,\) for which there are three possibilities: \(18 * 1,9 * 2,\) or \(6 * 3 .\) We'll try each of these factor pairs in place of the question marks:
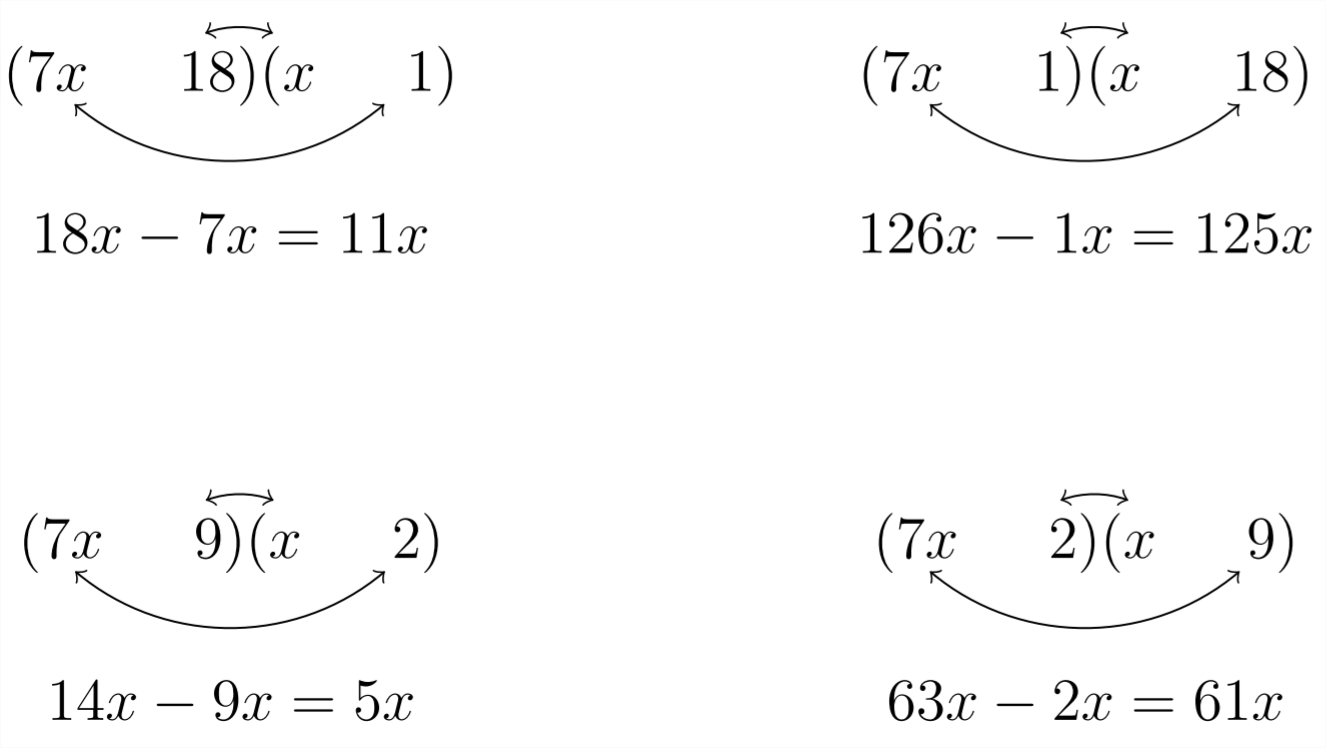

The choice above:
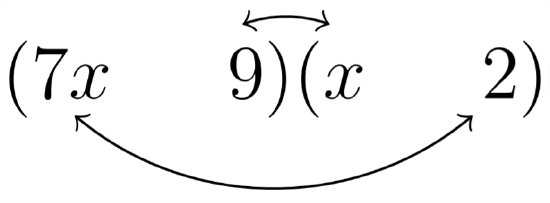
gives us the required \(5 x\) as the middle term. since we're looking for a \((-5 x),\) we'll make the 14 negative and the 9 positive: \(-14 x+9 x=-5 x\)
\[7 x^{2}-5 x-18=(7 x+9)(x-2) \nonumber\]
If we want to try the other method for factoring \(7 x^{2}-5 x-18\), we would multiply \(7 * 18=126,\) and then work to find factor pairs of 126 that have a difference of 5
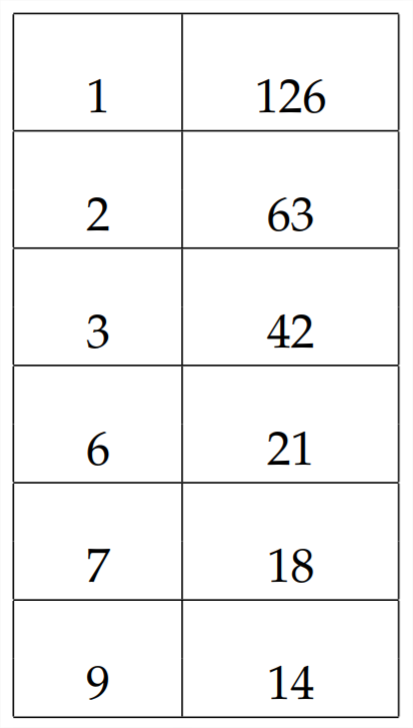
Here, the last factor pair, \(9 * 14\), has a difference of \(5 .\) So then we proceed to factor by grouping:
\[
\begin{aligned}
7 x^{2}-5 x-18 &=7 x^{2}+9 x-14 x-18 \\
&=x(7 x+9)-2(7 x+9) \\
&=(7 x+9)(x-2)
\end{aligned}
\]
Notice that when the -2 was factored out from the last two terms \(-14 x-18\), we ended up with \(-2(7 x+9)\), because \((-2) *(+9)=-18 .\) This is also important because in order to factor out the common binomial factor of \((7 x+9),\) this binomial must be exactly the same in both terms.
Difference of Squares
Factoring a difference of squares is actually a special form of trinomial factoring. If we consider a trinomial of the form \(a x^{2}+b x+c,\) where \(c\) is a perfect square and negative, we will find something interesting about the possible values of \(b\) that make the trinomial factorable.
Example
\[
\text { Consider } x^{2}+b x-36
\]
For this expression to be factorable, the middle coefficient \(b\) would need to be equal to the difference of any of the factor pairs of \(36 .\) If we look at the possible factor pairs, we see the following:
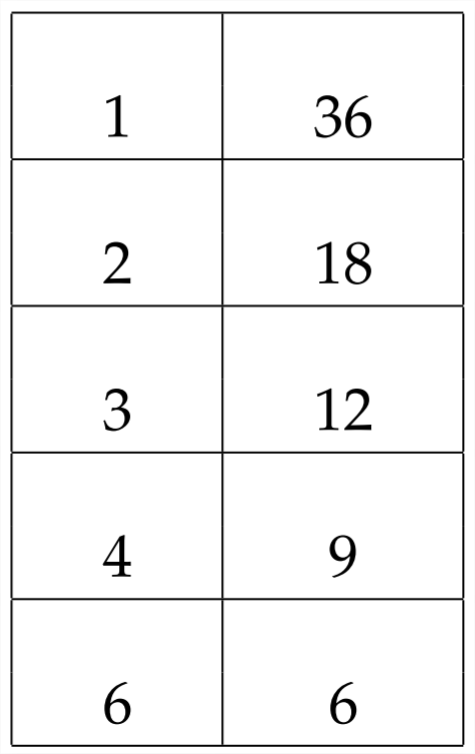
This means that the possible values for \(b\) that would make this expression factorable are:
\[
\begin{array}{c}
36-1=35 \rightarrow x^{2}+35 x-36=(x+36)(x-1) \\
18-2=16 \rightarrow x^{2}+16 x-36=(x+18)(x-2) \\
12-3=9 \rightarrow x^{2}+9 x-36=(x+12)(x-3) \\
9-4=5 \rightarrow x^{2}+5 x-36=(x+9)(x-4) \\
6-6=0 \rightarrow x^{2}+0 x-36=x^{2}-36=(x+6)(x-6)
\end{array}
\]
As we see, factoring \(x^{2}-36\) means that the factors of the perfect square \(36=6 * 6\) will cancel each other out leaving \(0 x\) in the middle. If there is a perfect square as the leading coefficient, then this number should be square rooted as well:
\[
16 x^{2}-25=(4 x+5)(4 x-5)
\]
In the example above, the \(+20 x\) and \(-20 x\) as the middle terms cancel each other out leaving just \(16 x^{2}-25\)
These three types of factoring can also be combined with each other as we see in the following examples.
Example \(\PageIndex{6}\)
Factor \(2 x^{2}-50\)
Solution
This is not a trinomial because it doesn't have three terms. It is also not a difference of squares because 2 and 50 are not perfect squares. However, there is a common factor of 2 which we can factor out:
\[
2 x^{2}-50=2\left(x^{2}-25\right)
\]
The expression inside the parentheses is a difference of squares and should be factored:
\[
2 x^{2}-50=2\left(x^{2}-25\right)=2(x+5)(x-5)
\]
Example \(\PageIndex{7}\)
Factor \(24-2 x-x^{2}\)
Solution
Here the sign of the \(x^{2}\) term is negative. For this problem we can factor out \(a-1\) and proceed as we did with the previous problems in which the leading coefficient was positive or we can factor it as it is:
\[
24-2 x-x^{2}=-\left(x^{2}+2 x-24\right)=-(x+6)(x-4)
\]
If we want to factor it as it is, we should be aware that the constant term is positive and the quadratic term is negative, which means that we will want the factors of 24 to have a difference of 2
\[
24-2 x-x^{2}=(6+x)(4-x)
\]
Example \(\PageIndex{8}\)
Factor \(6 x^{2}+12 x+6\)
Solution
First, we notice that this expression has a common factor of \(6 .\) If we factor out the
\(6,\) then we should be left with an easier problem:
\[
6 x^{2}+12 x+6=6\left(x^{2}+2 x+1\right)=6(x+1)(x+1)=6(x+1)^{2}
\]
Exercises \(\PageIndex{1}\)
Factor each expression completely.
1) \(\quad 8 a^{2} b^{3}+24 a^{2} b^{2}\)
2) \(\quad 19 x^{2} y-38 x^{2} y^{3}\)
3) \(\quad 13 t^{8}+26 t^{4}-39 t^{2}\)
4) \(\quad 5 y^{5}+25 y^{4}-20 y^{3}\)
5) \(\quad 45 m^{4} n^{5}+36 m n^{6}+81 m^{2} n^{3}\)
6) \(\quad125 x^{3} y^{5}+60 x^{4} y^{4}-85 x^{5} y^{2}\)
Factor each trinomial into the product of two binomials.
7) \(\quad a^{2}+3 a+2\)
8) \(\quad y^{2}-8 y-48\)
9) \(\quad x^{2}-6 x-27\)
10) \(\quad t^{2}-13 t+42\)
11) \(\quad m^{2}+3 m-54\)
12) \(\quad x^{2}+11 x+24\)
Factor completely. Remember to look first for a common factor. If the polynomial is prime, state this.
13) \(\quad a^{2}-9\)
14) \(\quad y^{2}-121\)
15) \(\quad -49+k^{2}\)
16) \(\quad -64+t^{2}\)
17) \(\quad 6 x^{2}-54\)
18) \(\quad 25 y^{2}-4\)
19) \(\quad 200-2 a^{2}\)
20) \(\quad 3 m^{2}-12\)
21) \(\quad 98-8 k^{2}\)
22) \(\quad -80 w^{2}+45\)
23) \(\quad 5 y^{2}-80\)
24) \(\quad -4 a^{2}+64\)
25) \(\quad 8 y^{2}-98\)
26) \(\quad 24 a^{2}-54\)
27) \(\quad 36 k-49 k^{3}\)
28) \(\quad 16 y-81 y^{3}\)
Factor each trinomial completely. Remember to look first for a common factor. If the polynomial is prime, state this.
29) \(\quad 3 y^{2}-15 y+16\)
30) \(\quad 8 a^{2}-14 a+3\)
31) \(\quad 9 x^{2}-18 x+8\)
32) \(\quad 6 a^{2}-17 a+12\)
33) \(\quad 2 x^{2}+7 x+6\)
34) \(\quad 2 m^{2}+13 m-18\)
35) \(\quad 20 y^{2}+22 y+6\)
36) \(\quad 36 x^{2}+81 x+45\)
37) \(\quad 24 a^{2}-42 a+9\)
38) \(\quad 48 x^{2}-74 x-10\)
Factor each expression completely.
39) \(\quad 30+7 y-y^{2}\)
40)\(\quad 45+4 a-a^{2}\)
41) \(\quad 24-10 x-x^{2}\)
42) \(\quad 36-9 x-x^{2}\)
43) \(\quad 84-8 x-x^{2}\)
44)\(\quad 72-6 a-a^{2}\)
45) \(\quad 6 y^{2}+24 y+15\)
46) \(\quad 10 y^{2}-75 y+35\)
47) \(\quad 20 a x^{2}-36 a x-8 a\)
- Answer
-
1) \(\quad 8 a^{2} b^{2}(b+3)\)
3) \(\quad 13 t^{2}\left(t^{6}+2 t^{2}-3\right)\)
5) \(\quad 9 m n^{3}\left(5 m^{3} n^{2}+4 n^{3}+9 m\right)\)
7) \(\quad (a+2)(a+1)\)
9) \(\quad (x-9)(x+3)\)
11) \(\quad (m+9)(m-6)\)
13) \(\quad (a+3)(a-3)\)
15) \(\quad (k+7)(k-7)\)
17) \(\quad 6(x+3)(x-3)\)
19) \(\quad 2(10+a)(10-a)\)
21) \(\quad 2(7+2 k)(7-2 k)\)
23) \(\quad 5(y+4)(y-4)\)
25) \(\quad 2(2 y+7)(2 y-7)\)
27) \(\quad k(6+7 k)(6-7 k)\)
29) \(\quad\) PRIME
31) \(\quad(3 x-4)(3 x-2)\)
33) \(\quad(2 x+3)(x+2)\)
35) \(\quad 2(5 y+3)(2 y+1)\)
37) \(\quad 3(2 a-3)(4 a-1)\)
39) \(\quad(10-y)(3+y)\)
41) \(\quad(12+x)(2-x)\)
43) \(\quad(14+x)(6-x)\)
45) \(\quad 3\left(2 y^{2}+8 y+5\right)\)
47) \(\quad 4 a(5 x+1)(x-2)\)


