5.3: Applications of the Parabola

Last updated
Save as PDF

Page ID: 40926

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A parabola that is rotated around its axis of symmetry to create a three dimensional object is called a paraboloid. One of the special properties of a parabola is that any light (or other electromagnetic wave) striking the interior of the parabola is reflected to the focus. The proof of this is somewhat complex, but this property makes the paraboloid a very useful shape in application.

The paraboloid is used to make satellite dishes so that the signal from the satellite is reflected to the center of the dish. This strengthens the signal. Parabolic microphones are often used at sporting events so that noises on the field can be heard more clearly on the sidelines. Flashlights and headlights also use this property in reverse. With the light at the focus of the paraboloid, all the light is reflected straight ahead, thus concentrating the beam of light.

One last application which has become used more frequently over the last five or ten years is the use of the paraboloid in solar power. One use of these properties sets up a tower at the focus of the paraboloid with mirrors banked around the tower in the paraboloid shape. This focuses all of the sun's power on the tower in the center. Often, salt is used in the tower since it has very high melting point. The salt is melted by the reflected sunlight and flows into a steam turbine. This has been found to be more efficient than just using standard solar panels.

Example
If a satellite dish is 8 feet across and $3 \mathrm{ft}$. deep, how far from the bottom of the dish should the receiver be placed so that it is at the focus of the paraboloid?
First let's consider what this looks like in two dimensions. Because we are setting up the graph of this parabola, we can choose to place the vertex at the origin. This makes things a little easier.
since the dish was a total of 8 feet across, we split this between the two sides of the graph, creating the points (4,3) and $(-4,3) .$ since the vertex for this parabola is at the origin, the standard equation is somewhat simplified.

Here's what this cross-section looks like:
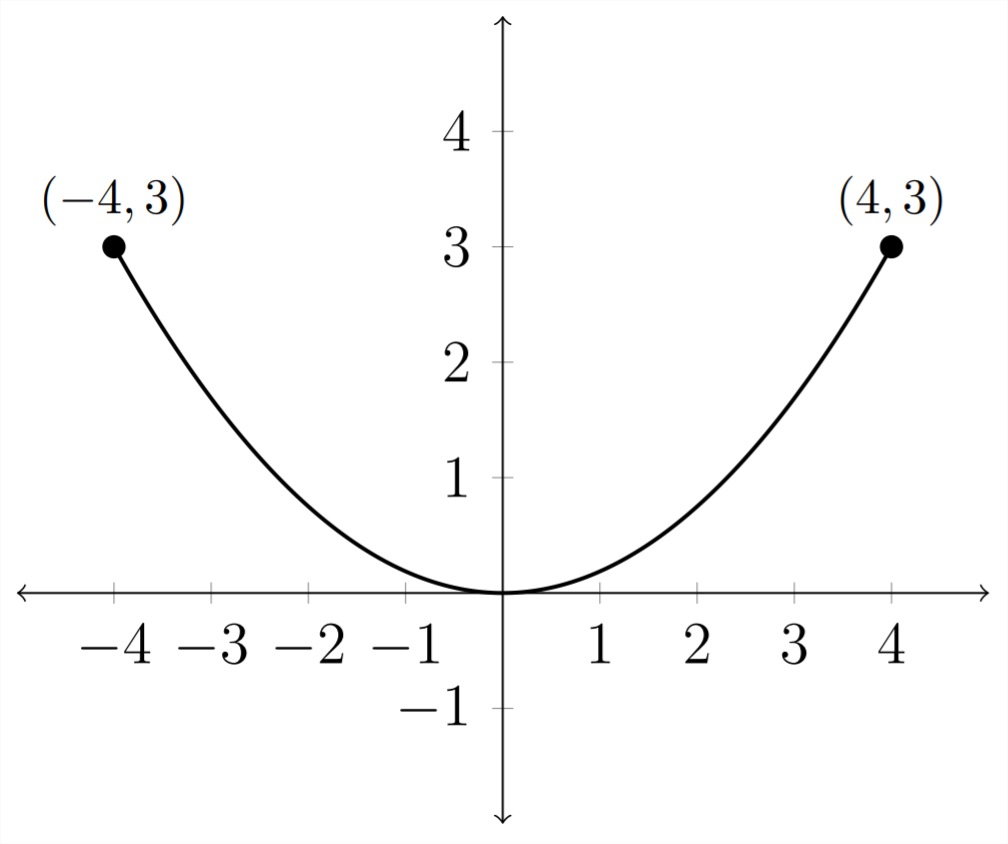
$clipboard_e45a8be0aba094446aefba1b4408d528b.png$
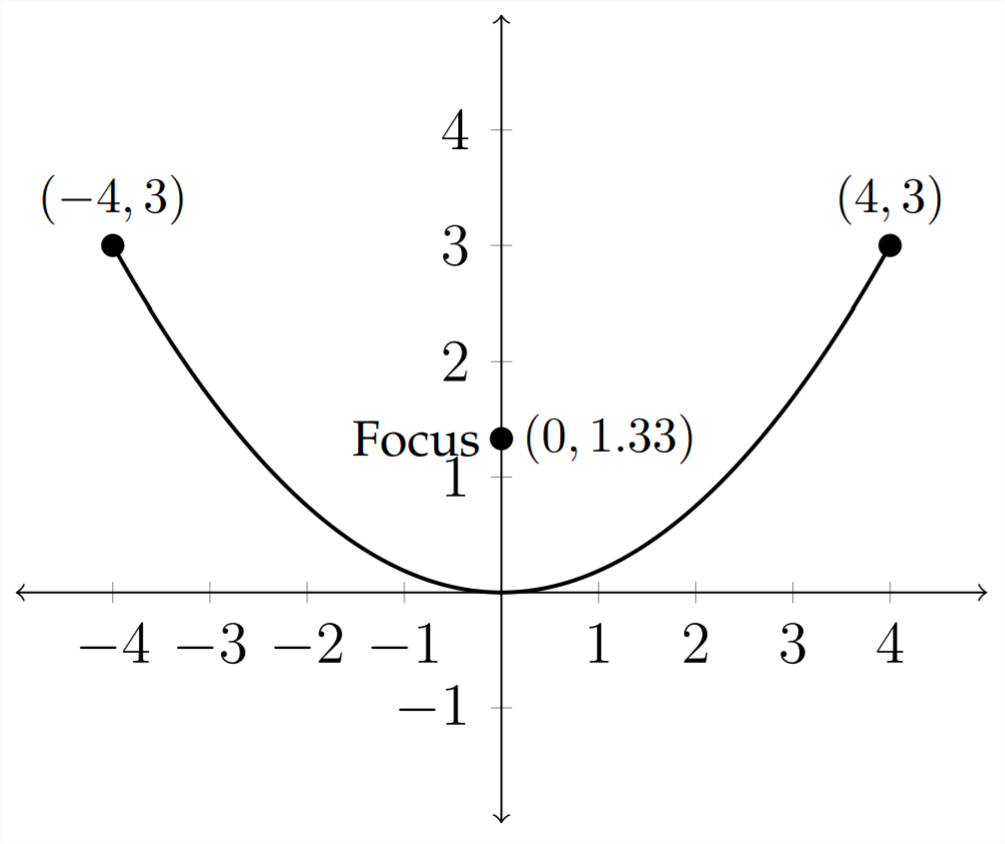
Taking the standard equation for an upward facing parabola: $4 p(y-k)=(x-h)^{2}$ and using the point (0,0) for the vertex leaves us with $4 p(y-0)=(x-0)^{2}$ or $4 p y=x^{2}$
The main thing we need to do is find the value of $p$ for this situation. This will tell us where the receiver should be on the satellite dish. Plugging in the points on the graph that we know will allow us to solve for $p$
\[
\begin{aligned}
4 p y &=x^{2} \\
4 p(3) &=(4)^{2} \\
12 p &=16 \\
p &=\frac{4}{3}
\end{aligned}
\]
Thus the receiver should be $\frac{4}{3}$ feet or 1 foot 4 inches from the bottom of the dish.
$clipboard_ec0bf6d45c49ea73873d51a832e2521f3.png$

Exercises 5.3
1) A satellite dish in the shape of a paraboloid is $10 \mathrm{ft}$. across and 3 ft. deep. How far from the vertex at the bottom of the dish should the receiver be placed?
2) A satellite dish in the shape of a paraboloid is 6 ft. across and 2 ft. deep. How far from the vertex at the bottom of the dish should the receiver be placed?
3) The reflector in a flashlight in the shape of a paraboloid is 2 inches across and 1 inch deep. How far from the vertex at the bottom of the reflector should the light source be placed so that the light is reflected straight ahead?
4) The reflector in a flashlight in the shape of a paraboloid is 5 inches across and 3 inches deep. How far from the vertex at the bottom of the reflector should the light source be placed so that the light is reflected straight ahead?
5) A car headlight in the shape of a paraboloid has a bulb that is placed 1.25 inches from the vertex at the bottom of the headlight. If the headlight is 6 inches in diameter, how deep should the headlight be for the bulb to be at the focus of the paraboloid?
6) A spotlight in the shape of a paraboloid has a bulb that is placed 3 inches from the vertex at the bottom of the light housing. If the spotlight is 18 inches in diameter, how deep should the light be for the bulb to be at the focus of the paraboloid?
When a cable, chain or string hangs between two ends, it makes the shape of a catenary, which is generally described by an equation of the form:
\[
f(x)=\frac{e^{x}+e^{-x}}{2}
\]
However, when the cables of a suspension bridge support the weight of the roadbed on the bridge, the cables are pulled into the shape of a parabola.
7) The cables of a suspension bridge are in the shape of a parabola. The towers of the bridge that support the cable are $400 \mathrm{ft}$. apart and $600 \mathrm{ft}$. tall. If the cables touch the roadway at the center of the bridge mid-way between the towers, how high is the cable $75 \mathrm{ft}$. from the center of the bridge?
8) The cables of a suspension bridge are in the shape of a parabola. The towers of the bridge that support the cable are $800 \mathrm{ft}$. apart and $160 \mathrm{ft}$. tall. If the cables touch the roadway at the center of the bridge mid-way between the towers, how high is the cable $120 \mathrm{ft}$. from the center of the bridge?
9) A spotlight in the shape of a paraboloid has the light source $2.5 \mathrm{ft}$. from the vertex at the bottom of the light. If the depth of the spotlight housing is $4 \mathrm{ft}$, how wide should the face of the spotlight be?
10) A flashlight reflector in the shape of a paraboloid has a light source that is
0.5 inches from the vertex at the bottom of the reflector. How deep should the reflector be if the face of the flashlight is 3 inches in diameter?
11) The parabolic mirror for the Mount Palomar observatory telescope is 200 inches in diameter and the mirror is 3.75 inches deep at the center. How far from the center of the mirror is the focal point where the light is reflected?
12) A reflecting telescope contains a mirror in the shape of a paraboloid. If the mirror is 5 inches across at the opening and 2 inches deep, how far from the vertex at the bottom of the mirror is the focal point?
13) The cables of a suspension bridge are in the shape of a parabola. The towers of the bridge that support the cable are $500 \mathrm{ft}$. apart and $80 \mathrm{ft}$. tall. If the cables are 15 ft. above the roadway at the center of the bridge mid-way between the towers, how high is the cable $100 \mathrm{ft}$. from the center of the bridge?
14) The cables of a suspension bridge are in the shape of a parabola. The towers of the bridge that support the cable are $2000 \mathrm{ft}$. apart and $400 \mathrm{ft}$. tall. If the cables are $25 \mathrm{ft}$. above the roadway at the center of the bridge mid-way between the towers, how high is the cable $500 \mathrm{ft}$. from the center of the bridge?
15) A flashlight reflector housing in the shape of a paraboloid is 4 inches deep and 4 inches across at its widest point. How far from the vertex at the bottom of the housing should the light source be placed?
16) A flashlight reflector housing in the shape of a paraboloid is 8 inches in diameter with the light source placed 1 inch from the vertex at the bottom of the housing. How deep should the housing be for the light source to be placed at the focal point?
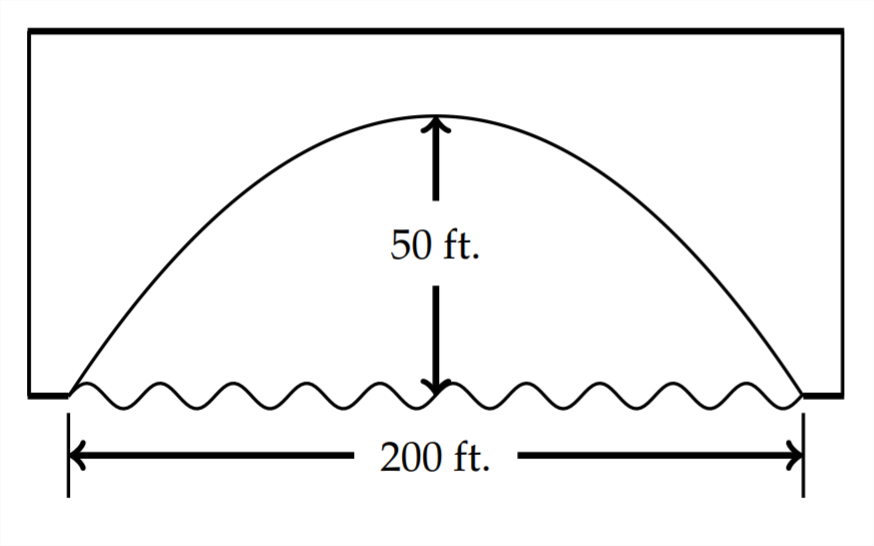
17) A bridge is built in the shape of a parabolic arch (see figure below). If the $\operatorname{arch}$ is $50 \mathrm{ft}$. above the water at the center and $200 \mathrm{ft}$. wide at the water's surface, will a boat that is 35 ft. tall clear the arch 30 ft. from the center? If not, how much taller than the bridge is the boat? If so, how much clearance will there be?
$clipboard_e9a359c29113aac390ce8b9eb073cce32.png$
18) A bridge is built in the shape of a parabolic arch. If the arch is 30 ft. above the water at the center and $150 \mathrm{ft}$. wide at the water's surface, find the height of the arch above the water at distances of $10,25,40,$ and $50 \mathrm{ft}$. from the center.