Preface
- Page ID
- 49279
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Preface
Elementary Algebra is a work text that covers the traditional topics studied in a modern elementary algebra course. It is intended for students who:
- This text can be used in standard lecture or self-paced classes. To help students meet these objectives and to make the study of algebra a pleasant and rewarding experience, Elementary Algebra is organized as follows.
Pedagogical Features
- Objectives
Sample SetsElementary Algebra contains examples that are set off in boxes for easy reference. The examples are referred to as Sample Sets for two reasons:
- A parallel Practice Set follows each Sample Set, which reinforces the concepts just learned. The answers to all Practice Sets are displayed with the question when viewing this content online, or at the end of the chapter in the print version.
Section ExercisesThe problems are paired so that the odd-numbered problems are equivalent in kind and difficulty to the even-numbered problems. Answers to the odd-numbered problems are provided with the exercise when viewed online, or at the back of the chapter in the print version.
Exercises for ReviewThis section consists of problems that form a cumulative review of the material covered in the preceding sections of the text and is not limited to material in that chapter. The exercises are keyed by section for easy reference.
Summary of Key ConceptsA summary of the important ideas and formulas used throughout the chapter is included at the end of each chapter. More than just a list of terms, the summary is a valuable tool that reinforces concepts in preparation for the Proficiency Exam at the end of the chapter, as well as future exams. The summary keys each item to the section of the text where it is discussed.
Exercise SupplementIn addition to numerous section exercises, each chapter includes approximately 100 supplemental problems, which are referenced by section. Answers to the odd-numbered problems are included with the problems when viewed online and in the back of the chapter in the print version.
Proficiency ExamEach chapter ends with a Proficiency Exam that can serve as a chapter review or a chapter evaluation. The proficiency Exam is keyed to sections, which enables the student to refer back to the text for assistance. Answers to all Proficiency Exam problems are included with the exercises when viewed online, or in the back of the chapter in the print version.
Content
The writing style is informal and friendly, offering a no-nonsense, straightforward approach to algebra. We have made a deliberate effort not to write another text that minimizes the use of words because we believe that students can be study algebraic concepts and understand algebraic techniques by using words and symbols rather than symbols alone. It has been our experience that students at the elementary level are not experienced enough with mathematics to understand symbolic explanations alone; they also need to read the explanation.
We have taken great care to present concepts and techniques so they are understandable and easily remembered. After concepts have been developed, students are warned about common pitfalls.
Arithmetic Review
This chapter contains many examples of arithmetic techniques that are used directly or indirectly in algebra. Since the chapter is intended as a review, the problem-solving techniques are presented without being developed. Therefore, no work space is provided, nor does the chapter contain all of the pedagogical features of the text. As a review, this chapter can be assigned at the discretion of the instructor and can also be a valuable reference tool for the student.
Basic Properties of Real Numbers
The symbols, notations, and properties of numbers that form the basis of algebra, as well as exponents and the rules of exponents, are introduced in Basic Properties of Real Numbers. Each property of real numbers and the rules of exponents are expressed both symbolically and literally. Literal explanations are included because symbolic explanations alone may be difficult for a student to interpret.
Basic Operations with Real Numbers
The basic operations with real numbers are presented in this chapter. The concept of absolute value is discussed both geometrically and symbolically. The geometric presentation offers a visual understanding of the meaning of ∣x∣. The symbolic presentation includes a literal explanation of how to use the definition. Negative exponents are developed, using reciprocals and the rules of exponents the student has already learned. Scientific notation is also included, using unique and real-life examples.
Algebraic Expressions and Equations
Operations with algebraic expressions and numerical evaluations are introduced in Algebraic Expressions and Equations. Coefficients are described rather than merely defined. Special binomial products have both literal symbolic explanation and since they occur so frequently in mathematics, we have been careful to help the student remember them. In each example problem, the student is “talked” through the symbolic form.
Solving Linear Equations and Inequalities
In this chapter, the emphasis is on the mechanics of equation solving, which clearly explains how to isolate a variable. The goal is to help the student feel more comfortable with solving applied problems. Ample opportunity is provided for the student to practice translating words to symbols, which is an important part of the “Five-Step Method” of solving applied problems (discussed in Section 5.6 and Section 5.7).
Factoring Polynomials
Factoring is an essential skill for success in algebra and higher level mathematics courses. Therefore, we have taken great care in developing the student’s understanding of the factorization process. The technique is consistently illustrated by displaying an empty set of parentheses and describing the thought process used to discover the terms that are to be placed inside the parentheses.
The factoring scheme for special products is presented with both verbal and symbolic descriptions, since not all students can interpret symbolic descriptions alone. Two techniques, the standard “trial and error” method, and the “collect and discard” method (a method similar to the “ac” method), are presented for factoring trinomials with leading coefficients different from 1.
Graphing Linear Equations and Inequalities in One and Two Variables
In this chapter the student is shown how graphs provide information that is not always evident from the equation alone. The chapter begins by establishing the relationship between the variables in an equation, the number of coordinate axes necessary to construct the graph, and the spatial dimension of both the coordinate system and the graph. Interpretation of graphs is also emphasized throughout the chapter, beginning with the plotting of points. The slope formula is fully developed, progressing from verbal phrases to mathematical expressions. The expressions are then formed into an equation by explicitly stating that a ratio is a comparison of two quantities of the same type (e.g., distance, weight, or money). This approach benefits students who take future courses that use graphs to display information.
The student is shown how to graph lines using the intercept method, the table method, and the slope-intercept method, as well as how to distinguish, by inspection, oblique and horizontal/vertical lines.
Rational Expressions
A detailed study of arithmetic operations with rational expressions is presented in this chapter, beginning with the definition of a rational expression and then proceeding immediately to a discussion of the domain. The process of reducing a rational expression and illustrations of multiplying, dividing, adding, and subtracting rational expressions are also included. Since the operations of addition and subtraction can cause the most difficulty, they are given particular attention. We have tried to make the written explanation of the examples clearer by using a “freeze frame approach.
The five-step method of solving applied problems is included in this chapter to show the problem-solving approach to number problems, work problems, and geometry problems. The chapter also illustrates simplification of complex rational expressions, using the combine-divide method and the LCD-multiply-divide method.
Roots, Radicals, and Square Root Equations
The distinction between the principal square root of the number x ,
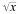, and the secondary square root of the number
x
, 
, is made by explanation and by example. The simplification of radical expressions that both involve and do not involve fractions is shown in many detailed examples; this is followed by an explanation of how and why radicals are eliminated from the denominator of a radical expression. Real-life applications of radical equations have been included, such as problems involving daily output, daily sales, electronic resonance frequency, and kinetic energy.Quadratic Equations
Methods of solving quadratic equations as well as the logic underlying each method are discussed. Factoring, extraction of roots, completing the square, and the quadratic formula are carefully developed. The zero-factor property of real numbers is reintroduced. The chapter also includes graphs of quadratic equations based on the standard parabola, y = x2 , and applied problems from the areas of manufacturing, population, physics, geometry, mathematics (number and volumes), and astronomy, which are solved using the five-step method.
Systems of Linear Equations
Beginning with the graphical solution of systems, this chapter includes an interpretation of independent, inconsistent, and dependent systems and examples to illustrate the applications for these systems. The substitution method and the addition method of solving a system by elimination are explained, noting when to use each method. The five-step method is again used to illustrate the solutions of value and rate problems (coin and mixture problems), using drawings that correspond to the actual solution.
- A parallel Practice Set follows each Sample Set, which reinforces the concepts just learned. The answers to all Practice Sets are displayed with the question when viewing this content online, or at the end of the chapter in the print version.
- Objectives