1.2: Factors, Products, and Exponents
- Page ID
- 49338
Overview
- Factors
- Exponential Notation
Factors
Let’s begin our review of arithmetic by recalling the meaning of multiplication for whole numbers (the counting numbers and zero)
Multiplication
Multiplication is a description of repeated addition.
In the addition
\(7+7+7+7 \)
the number 7 is repeated as an addend* 4 times. Therefore, we say we have four times seven and describe it by writing
\(4 · 7\)
The raised dot between the numbers 4 and 7 indicates multiplication. The dot directs us to multiply the two numbers that it separates. In algebra, the dot is preferred over the symbol × to denote multiplication because the letter x is often used to represent a number. Thus,
\(4 · 7=7+7+7+7\)
Factors and Products
In multiplication, the numbers being multiplied are called factors. The result of a multiplication is called the product. For example, in the multiplication
\(4 · 7=28 \)
the numbers 4 and 7 are factors, and the number 28 is the product. We say that 4 and 7 are factors of 28. (They are not the only factors of 28. Can you think of others?)
Now we know that
(factor) · (factor) = product
This indicates that a first number is a factor of a second number if the first number divides into the second number with no remainder. For example, since
\(4 · 7=28\)
both 4 and 7 are factors of 28 since both 4 and 7 divide into 28 with no remainder.
Exponential Notation
Quite often, a particular number will be repeated as a factor in a multiplication. For example, in the multiplication
\(7 · 7 · 7 · 7\)
the number 7 is repeated as a factor 4 times. We describe this by writing \(7^{4}\). Thus,
\(7 · 7 · 7 · 7=7^4\)
The repeated factor is the lower number (the base), and the number recording how many times the factor is repeated is the higher number (the superscript). The superscript number is called an exponent.
An exponent is a number that records how many times the number to which it is attached occurs as a factor in a multiplication.
Sample Set A
For Examples 1, 2, and 3, express each product using exponents.
\(3 · 3 · 3 · 3 · 3 · 3\) Since 3 occurs as a factor 6 times,
\(3 · 3 · 3 · 3 · 3 · 3=3^6\)
\(8 · 8\) Since 8 occurs as a factor 2 times,
\(8 · 8=8^2\)
\(5 · 5 · 5 · 9 · 9\) Since 5 occurs as a factor 3 times, we have \(5^{3}\) . Since 9 occurs as a factor 2 times, we have \(9^{2}\). We should see the following replacements.
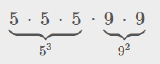
Then we have
\(5 · 5 · 5 · 9 · 9=5^3 · 9^2\)
Expand \(3^{5}\) . The base is 3 so it is the repeated factor. The exponent is 5 and it records the number of times the base 3 is repeated. Thus, 3 is to be repeated as a factor 5 times.
\(3^5 =3 · 3 · 3 · 3 · 3\)
Expand \(6^{2}\) · \(10^{4}\). The notation \(6^{2}\) · \(10^{4}\) records the following two facts: 6 is to be repeated as a factor 2 times and 10 is to be repeated as a factor 4 times. Thus,
\(6^2 · 10^4=6 · 6 · 10 · 10 · 10 · 10\)
Exercises
For the following problems, express each product using exponents.
8 · 8 · 8
- Answer
-
\(8^3\)
12 · 12 · 12 · 12 · 12
- Answer
-
\(12^5\)
1 · 1
- Answer
-
\(1^2\)
3 · 3 · 3 · 3 · 3 · 4 · 4
- Answer
-
\(3^5\) · \(4^2\)
2 · 2 · 2 · 9 · 9 · 9 · 9 · 9 · 9 · 9 · 9
- Answer
-
\(2^3\) · \(9^8\)
3 · 3 · 10 · 10 · 10
- Answer
-
\(3^2\) · \(10^3\)
3 · 3 · 3 · 4 · 4
- Answer
-
\(3^5\) · \(4^2\)
Suppose that the letters x and y are each used to represent numbers. Use exponents to express the following product.
\(x\) · \(x\) · \(x\) · \(y\) · \(y\)
- Answer
-
\(x^3\) · \(y^2\)
\(x\)· \(x\)· \(x\)· \(x\)· \(x\)· \(y\)· \(y\)· \(y\)
- Answer
-
\(x^5\) · \(y^3\)
For the following problems, expand each product (do not compute the actual value).
\(3^4\)
- Answer
-
3 · 3 · 3 · 3
\(4^3\)
- Answer
-
4 · 4 · 4
\(2^5\)
- Answer
-
2 · 2 · 2 · 2 · 2
\(9^6\)
- Answer
-
9 · 9 · 9 · 9 · 9 · 9
\(5^3\) · \(6^2\)
- Answer
-
5 · 5 · 5 · 6 · 6
\(2^7\) · \(3^4\)
- Answer
-
2 · 2 · 2 · 2 · 2 · 2 · 2 · 3 · 3 · 3 · 3
\(x^4\) · \(y^4\)
- Answer
-
\(x\) · \(x\) · \(x\) · \(x\) · \(y\) · \(y\) · \(y\) · \(y\)
\(x^6\) · \(y^2\)
- Answer
-
\(x\) · \(x\) · \(x\) · \(x\) · \(x\) · \(x\) · \(y\) · \(y\)
For the following problems, specify all the whole number factors of each number. For example, the complete set of whole number factors of 6 is 1, 2, 3, 6.
20
- Answer
-
1, 2, 4, 5, 10, 20
14
- Answer
-
1, 2, 7, 14
12
- Answer
-
1, 2, 3, 4, 6, 12
30
- Answer
-
1, 2, 3, 5, 6, 10, 15, 30
21
- Answer
-
1, 3, 7, 21
45
- Answer
-
1, 3, 5, 9, 15, 45
11
- Answer
-
1, 11
17
- Answer
-
1, 17
19
- Answer
-
1, 19
2
- Answer
-
1, 2


