2.5: Exponents
- Page ID
- 49349
Overview
- Exponential Notation
- Reading Exponential Notation
- The Order of Operations
Exponential Notation
In Section 2.4 we were reminded that multiplication is a description for repeated addition. A natural question is "Is there a description for repeated multiplication?" The answer is yes. The notation that describes repeated multiplication is exponential notation.
Factors
In multiplication, the numbers being multiplied together are called factors. In repeated multiplication, all the factors are the same. In nonrepeated multiplication, none of the factors are the same. For example,
\(18 \cdot 18 \cdot 18 \cdot 18\) Repeated Multiplication of 18. All four factors, 18 are the same.
\(x \cdot x \cdot x \cdot x \cdot x\) Repeated multiplication of \(x\). All five factors, \(x\), are the same.
\(3 \cdot 7 \cdot a\) Nonrepeated multiplication. None of the factors are the same.
Exponential notation is used to show repeated multiplication of the same factor. The notation consists of using a superscript on the factor that is repeated. The superscript is called an exponent.
Exponential Notation If \(x\) is any real number and \(n\) is a natural number, then
\(x^{n}=\underbrace{x \cdot x \cdot x \cdot \ldots \cdot x}_{n \text { factors of } x}\)
An exponent records the number of identical factors in multiplication.
Note that the definition for exponential notation only has meaning for natural number exponents. We will extend this notation to include other numbers as exponents later.
Sample Set A
\(7 \cdot 7 \cdot 7 \cdot 7 \cdot 7 \cdot 7 = 7^6\)
The repeated factor is 7. The exponent 6 records the fact that 7 appears 6 times in the multiplication.
\(x \cdot x \cdot x \cdot x = x^4\)
The repeated factor is \(x\). The exponent 4 records the fact that \(x\) appears 4 times in the multiplication.
\((2y)(2y)(2y) = (2y)^3\)
The repeated factor is \(2y\). The exponent 3 records the fact that the factor \(2y\) appears 3 times in the multiplication.
\(2yyy = 2y^3\)
The repeated factor is \(y\). The exponent 3 records the fact that the factor \(y\) appears 3 times in the multiplication.
\((a + b)(a + b)(a - b)(a - b)(a - b) = (a + b)^2(a - b)^3\)
The repeated factors are \((a + b)\) and \((a - b)\), \((a + b)\) appearing 2 times and \((a - b)\) appearing 3 times.
Practice Set A
Write each of the following using exponents.
\(a \cdot a \cdot a \cdot a\)
- Answer
-
\(a^4\)
\((3b)(3b)(5c)(5c)(5c)(5c)\)
- Answer
-
\((3b)^2(5c)^4\)
\(2 \cdot 2 \cdot 7 \cdot 7 \cdot 7 \cdot (a - 4)(a - 4)\)
- Answer
-
\(2^2 \cdot 7^3(a - 4)^2\)
\(8xxxyzzzzz\)
- Answer
-
\(8x^3yz^5\)
Sample Set B
\(8x^3\) means \(8 \cdot xxx\) and not \(8x8x8x\). The exponent \(3\) applies only to the factor \(x\) since it is only to the factor \(x\) that the \(3\) is connected.
\((8x)^3\) means \((8x)(8x)(8x)\) since the parentheses indicate that the exponent \(3\) is directly connected to the factor \(8x\). Remember that the grouping symbols ( ) indicate that the quantities inside are to be considered as one single number.
\(34(a+1)^2\) means \(34 \cdot (a+1)(a+1)\) since the exponent \(2\) applies only to the factor \((a+1)\).
Practice Set B
Write each of the following without exponents.
\(4a^3\)
- Answer
-
\(4aaa\)
\((4a)^3\)
- Answer
-
\((4a)(4a)(4a)\)
Sample Set C
Select a number to show that \((2 x)^{2}\) is not always equal to \(2 x^{2}\).
Suppose we choose \(x\) to be 5 . Consider both \((2 x)^{2}\) and \(2 x^{2}\).
\(
\begin{array}{ll}
(2 x)^{2} & 2 x^{2} \\
(2 \cdot 5)^{2} & 2 \cdot 5^{2} \\
(10)^{2} & 2 \cdot 25 \\
100 & \neq 50
\end{array}
\)
Notice that \((2 x)^{2}=2 x^{2}\) only when \(x=0\).
Practice Set C
Select a number to show that \((5x)^2\) is not always equal to \(5x^2\)
- Answer
-
Select \(x=3\). Then \((5 \cdot 3)^2 = (15)^2 = 225\), but \(5 \cdot 3^2 = 5 \cdot 9 = 45\). \(225 \not = 45\)
Reading Exponential Notation
\(ln(x^n)\)
Base
\(x\) is the base.
Exponent
\(n\) is the exponent.
Power
The number represented by \(x^n\) is called a power.
\(x\) to the \(n\)th Power
The term \(x^n\) is read as "\(x\) to the \(n\)th power," or more simply as "\(x\) to the \(n\)th."
\(x\) Squared and \(x\) Cubed
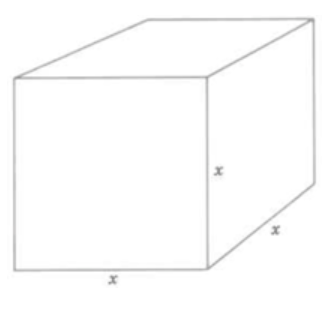
The symbol \(x^2\) is often read as "\(x\) squared," and \(x^3\) is often read as "\(x\) cubed." A natural question is "Why are geometric terms appearing in the exponent expression?" The answer for \(x^3\) is this: \(x^3\) means \(x \cdot x \cdot x\). In geometry, the volume of a rectangular box is found by multiplying the length by the width by the depth. A cube has the same length on each side. If we represent this length by the letter \(x\) then the volume of the cube is \(x \cdot x \cdot x\), which, of course, is described by \(x^3\). (Can you think of why \(x^2\) is read as \(x\) squared?)
Cube with
length = \(x\)
width = \(x\)
depth = \(x\)
Volume = \(xxx\) = \(x^3\)
The Order of Operations
In Section 4.2 we were introduced to the order of operations. It was noted that we would insert another operation before multiplication and division. We can do that now.
- Perform all operations inside grouping symbols beginning with the innermost set.
- Perform all exponential operations as you come to them, moving left-to-right.
- Perform all multiplications and divisions as you come to them, moving left-to-right.
- Perform all additions and subtractions as you come to them, moving left-to-right.
Sample Set D
Use the order of operations to simplify each of the following.
\(2^2 + 5 = 4 + 5 = 9\)
\(5^2 + 3^2 + 10 = 25 + 9 + 10 = 44\)
\(
\begin{aligned}
2^{2}+(5)(8)-1 &=4+(5)(8)-1 \\
&=4+40-1 \\
&=43
\end{aligned}
\)
\(
\begin{aligned}
7 \cdot 6-4^{2}+1^{5} &=7 \cdot 6-16+1 \\
&=42-16+1 \\
&=27
\end{aligned}
\)
\(
\begin{aligned}
(2+3)^{3}+7^{2}-3(4+1)^{2} &=(5)^{3}+7^{2}-3(5)^{2} \\
&=125+49-3(25) \\
&=125+49-75
\end{aligned}
\)
\(
\begin{aligned}
\left[4(6+2)^{3}\right]^{2} &=\left[4(8)^{3}\right]^{2} \\
&=[4(512)]^{2} \\
&=[2048]^{2} \\
&=4,194,304
\end{aligned}
\)
\(
\begin{aligned}
6\left(3^{2}+2^{2}\right)+4^{2} &=6(9+4)+4^{2} \\
&=6(13)+4^{2} \\
&=6(13)+16 \\
&=78+16 \\
&=94
\end{aligned}
\)
\(
\begin{aligned}
\dfrac{6^{2}+2^{2}}{4^{2}+6 \cdot 2^{2}}+\dfrac{1^{3}+8^{2}}{10^{2}-(19)(5)} &=\dfrac{36+4}{16+6 \cdot 4}+\dfrac{1+64}{100-95} \\
&=\dfrac{36+4}{16+24}+\dfrac{1+64}{100-95} \\
&=\dfrac{40}{40}+\dfrac{65}{5} \\
&=1+13 \\
&=14
\end{aligned}
\)
Practice Set D
Use the order of operations to simplify the following.
\(3^2 + 4 \cdot 5\)
- Answer
-
29
\(2^3 + 3^3 - 8 \cdot 4\)
- Answer
-
3
\(1^4 + (2^2 + 4)^2 \div 2^3\)
- Answer
-
9
\([6(10 - 2^3)]^2 - 10^2 - 6^2\)
- Answer
-
8
\(\dfrac{5^2 + 6^2 - 10}{1 + 4^2} + \dfrac{0^4 - 0^5}{7^2 - 6 \cdot 2^3}\)
- Answer
-
3
Exercises
For the following problems, write each of the quantities using exponential notation.
\(b\) to the fourth
- Answer
-
\(b^4\)
\(a\) squared
\(x\) to the eighth
- Answer
-
\(x^8\)
\((-3)\) cubed
\(5\) times \(s\) squared
- Answer
-
\(5s^2\)
\(3\) squared times \(y\) to the fifth
\(a\) cubed minus \((b + 7)\) squared
- Answer
-
\(a^3 - (b + 7)^2\)
\((21 - x)\) cubed plus \(x + 5\) to the seventh
\(xxxxx\)
- Answer
-
\(x^5\)
\((8)(8)xxxx\)
\(2 \cdot 3 \cdot 3 \cdot 3 \cdot 3xxyyyyy\)
- Answer
-
\(2(3^4)x^2y^5\)
\(2 \cdot 2 \cdot 5 \cdot 6 \cdot 6 \cdot 6xyyzzzwwww\)
\(7xx(a + 8)(a + 8)\)
- Answer
-
\(7x^2(a + 8)^2\)
\(10xyy(c + 5)(c + 5)(c + 5)\)
\(4x4x4x4x4x\)
- Answer
-
\((4x)^5\) or \(4^5x^5\)
\((9a)(9a)(9a)(9a)\)
\((-7)(-7)(-7)aabbba(-7)baab\)
- Answer
-
\((-7)^4a^5b^5\)
\((a - 10)(a - 10)(a + 10)\)
\((z + w)(z + w)(z + w)(z - w)(z - w)\)
- Answer
-
\((z + w)^3(z - w)^2\)
\((2y)(2y)2y2y\)
\(3xyxxy - (x + 1)(x + 1)(x + 1)\)
- Answer
-
\(3x^3y^2 - (x + 1)^3\)
For the following problems, expand the quantities so that no exponents appear.
\(4^3\)
\(6^2\)
- Answer
-
\(6 \cdot 6\)
\(7^3y^2\)
\(8x^3y^2\)
- Answer
-
\(8 \cdot x \cdot x \cdot x \cdot y \cdot y\)
\((18x^2y^4)^2\)
\((9a^3b^2)^3\)
- Answer
-
\((9aaabb)(9aaabb)(9aaabb)\) or \(9 \cdot 9 \cdot 9aaaaaaaaabbbbbb\)
\(5x^2(2y^3)^3\)
\(10a^3b^2(3c)^2\)
- Answer
-
\(10aaabb(3c)(3c)\) or \(10 \cdot 3 \cdot 3aaabbcc\)
\((a + 10)^2(a^2 + 10)^2\)
\((x^2 - y^2)(x^2 + y^2)\)
- Answer
-
\((xx - yy)(xx + yy)\)
For the following problems, select a number (or numbers) to show that
\((5x)^2\) is not generally equal to \(5x^2\).
\((7x)^2\) is not generally equal to \(7x^2\)
- Answer
-
Select \(x = 2\). Then, \(196 \not = 28\)
\((a + b)^2\) is not generally equal to \(a^2 + b^2\)
For what real number is \((6a)^2\) equal to \(6a^2\)
- Answer
-
\(0\)
For what real numbers, \(a\) and \(b\), is \((a + b)^2\) equal to \(a^2 + b^2\).
Use the order of operations to simplify the quantities for the following problems.
\(3^2 + 7\)
- Answer
-
\(16\)
\(4^3 - 18\)
\(5^2 + 2(40)\)
- Answer
-
\(105\)
\(8^2 + 3 + 5(2 + 7)\)
\(2^5 + 3(8 + 1)\)
- Answer
-
\(59\)
\(3^4 + 2^4(1 + 5)^3\)
\((6^2 - 4^2) \div 5\)
- Answer
-
\(4\)
\(2^2(10 - 2^3)\)
\((3^4 - 4^3) \div 17\)
- Answer
-
\(1\)
\((4 + 3)^2 + 1 \div (2 \cdot 5\)
\((2^4 + 2^5 - 2^3 \cdot 5)^2 \div 4^2\)
- Answer
-
\(4\)
\(1^6 + 0^8 + 5^2(2 + 8)^3\)
\((7)(16) - 9^2 + 4(1^1 + 3^2)\)
- Answer
-
\(71\)
\(\dfrac{2^3 - 7}{5^2}\)
\(\dfrac{(1 + 6)^2 + 2}{19}\)
- Answer
-
\(\dfrac{51}{19}\)
\(\dfrac{6^2 - 1}{5} + \dfrac{4^3 + (2)(3)}{10}\)
\(\dfrac{(2 + 1)^3 + 2^3 + 1^3}{6^2} - \dfrac{15^2 - [2(5)]^2}{5 \cdot 5^2}\)
\(\dfrac{6^3 - 2 \cdot 10^2}{2^2} + \dfrac{18(2^3 + 7^2)}{2(19) - 3^3}\)
- Answer
-
\(\dfrac{1070}{11}\) or \(97.27\)
Exercises for Review
Use algebraic notation to write the statement "a number divided by eight, plus five, is equal to ten."
Draw a number line that extends from −5 to 5 and place points at all real numbers that are strictly greater than −3 but less than or equal to 2.
- Answer
-
Is every integer a whole number?
Use the commutative property of multiplication to write a number equal to the number \(yx\).
- Answer
-
\(xy\)
Use the distributive property to expand \(3(x+6)\).