2.5: Applications of Linear Equations
- Page ID
- 18337
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify key words and phrases, translate sentences to mathematical equations, and develop strategies to solve problems.
- Solve word problems involving relationships between numbers.
- Solve geometry problems involving perimeter.
- Solve percent and money problems including simple interest.
- Set up and solve uniform motion problems.
Key Words, Translation, and Strategy
Algebra simplifies the process of solving real-world problems. This is done by using letters to represent unknowns, restating problems in the form of equations, and offering systematic techniques for solving those equations. To solve problems using algebra, first translate the wording of the problem into mathematical statements that describe the relationships between the given information and the unknowns. Usually, this translation to mathematical statements is the difficult step in the process. The key to the translation is to carefully read the problem and identify certain key words and phrases.
| Key Words | Translation |
|---|---|
| Sum, increased by, more than, plus, added to, total | \(+\) |
| Difference, decreased by, subtracted from, less, minus | \(-\) |
| Product, multiplied by, of, times, twice | \(*\) |
| Quotient, divided by, ratio, per | \(/\) |
| Is, total, result | \(=\) |
Here are some examples of translated key phrases.
| Key Phrases | Translation |
|---|---|
| The sum of a number and 7. |
\(x+7\) |
| Seven more than a number. | |
| The difference of a number and 7. |
\(x-7\) |
| Seven less than a number. | |
| Seven subtracted from a number. | |
| The product of 2 and a number. |
\(2x\) |
| Twice a number. | |
| One-half of a number. | \(\frac{1}{2}x\) |
| The quotient of a number and 7. | \(\frac{x}{7}\) |
When translating sentences into mathematical statements, be sure to read the sentence several times and identify the key words and phrases.
Translate:
Four less than twice some number is \(16\).
Solution:
First, choose a variable for the unknown number and identify the key words and phrases. Let \(x\) represent the unknown indicated by “some number.”
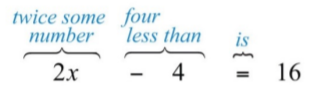.png?revision=1)
Figure \(\PageIndex{1}\)
Remember that subtraction is not commutative. For this reason, take care when setting up differences. In this example, \(4−2x=16\) is an incorrect translation.
Answer:
\(2x−4=16\)
It is important to first identify the variable—let x represent…—and state in words what the unknown quantity is. This step not only makes your work more readable but also forces you to think about what you are looking for. Usually, if you know what you are asked to find, then the task of finding it is achievable.
Translate:
When \(7\) is subtracted from \(3\) times the sum of a number and \(12\), the result is \(20\).
Solution:
Let \(n\) represent the unknown number.
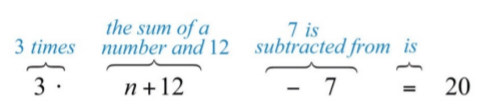.png?revision=1)
Figure \(\PageIndex{2}\)
Answer:
\(3(n+12)−7=20\)
To understand why parentheses are needed, study the structures of the following two sentences and their translations:
| “3 times the sum of a number and 12” | \(3(n+12)\) |
| “the sum of 3 times a number and 12” | \(3n+12\) |
The key is to focus on the phrase “3 times the sum.” This prompts us to group the sum within parentheses and then multiply by 3. Once an application is translated into an algebraic equation, solve it using the techniques you have learned.
- Step 1: Read the problem several times, identify the key words and phrases, and organize the given information.
- Step 2: Identify the variables by assigning a letter or expression to the unknown quantities.
- Step 3: Translate and set up an algebraic equation that models the problem.
- Step 4: Solve the resulting algebraic equation.
- Step 5: Finally, answer the question in sentence form and make sure it makes sense (check it).
For now, set up all of your equations using only one variable. Avoid two variables by looking for a relationship between the unknowns.
Problems Involving Relationships between Real Numbers
We classify applications involving relationships between real numbers broadly as number problems. These problems can sometimes be solved using some creative arithmetic, guessing, and checking. Solving in this manner is not a good practice and should be avoided. Begin by working through the basic steps outlined in the general guidelines for solving word problems.
A larger integer is \(2\) less than \(3\) times a smaller integer. The sum of the two integers is \(18\). Find the integers.
Solution:
Identify variables: Begin by assigning a variable to the smaller integer.
Let \(x\) represent the smaller integer.
Use the first sentence to identify the larger integer in terms of the variable \(x\): “A larger integer is 2 less than 3 times a smaller.”
Let \(3x-2\) represent the larger integer.
Set up an equation: Add the expressions that represent the two integers, and set the resulting expression equal to \(18\) as indicated in the second sentence: “The sum of the two integers is \(18\).”
\(x+(3x-2)=18\)
Solve: Solve the equation to obtain the smaller integer \(x\).
\(\begin{aligned} x+(3x-2)&=18 \\ x+3x-2&=18 \\ 4x-2&=18 \\ 4x-2\color{Cerulean}{+2}&=18\color{Cerulean}{+2} \\ 4x&=20 \\ \frac{4x}{\color{Cerulean}{4}}&=\frac{20}{\color{Cerulean}{4}} \\ x&=5 \end{aligned}\)
Back substitute: Use the expression \(3x−2\) to find the larger integer—this is called back substituting.
\(3x-2=3(\color{OliveGreen}{5}\color{black}{)-2=15-2=13}\)
Answer the question: The two integers are \(5\) and \(13\).
Check: \(5 + 13 = 18\). The answer makes sense.
The difference between two integers is \(2\). The larger integer is \(6\) less than twice the smaller. Find the integers.
Solution:
Use the relationship between the two integers in the second sentence, “The larger integer is 6 less than twice the smaller,” to identify the unknowns in terms of one variable.
Let \(x\) represent the smaller integer.
Let \(2x-6\) represent the larger integer.
Since the difference is positive, subtract the smaller integer from the larger.
\((2x-6)-x=2\)
Solve.
\(\begin{aligned} \color{OliveGreen}{2x}\color{black}{-6}\color{OliveGreen}{-x}&=2 \\ x-6&=2 \\ x-6\color{Cerulean}{+6}&=2\color{Cerulean}{+6} \\ x&=8 \end{aligned}\)
Use \(2x − 6\) to find the larger integer.
\(2x-6=2(\color{Cerulean}{8}\color{black}{)-6=16-6=10}\)
Answer:
The two integers are \(8\) and \(10\). These integers clearly solve the problem.
It is worth mentioning again that you can often find solutions to simple problems by guessing and checking. This is so because the numbers are chosen to simplify the process of solving, so that the algebraic steps are not too tedious. You learn how to set up algebraic equations with easier problems, so that you can use these ideas to solve more difficult problems later.
The sum of two consecutive even integers is \(46\). Find the integers.
Solution:
The key phrase to focus on is “consecutive even integers.”
Let \(x\) represent the first even integer.
Let \(x+2\) represent the next even integer.
Add the even integers and set them equal to \(46\).
\(x+(x+2)=46\)
Solve.
\(\begin{aligned}\color{OliveGreen}{x+x}\color{black}{+2}&=46\\2x+2&=46\\2x+2\color{Cerulean}{-2}&=46\color{Cerulean}{-2}\\2x&=44\\x&=22 \end{aligned}\)
Use \(x + 2\) to find the next even integer.
\(x+2=\color{Cerulean}{22}\color{black}{+2=24}\)
Answer:
The consecutive even integers are \(22\) and \(24\).
It should be clear that consecutive even integers are separated by two units. However, it may not be so clear that odd integers are as well.
.png?revision=1)
Figure \(\PageIndex{3}\)
The sum of two consecutive odd integers is \(36\). Find the integers.
Solution:
The key phrase to focus on is “consecutive odd integers.”
Let \(x\) represent the first odd integer.
Let \(x+2\) represent the next odd integer.
Add the two odd integers and set the expression equal to \(36\).
\(x+(x+2)=36\)
Solve.
\(\begin{aligned} \color{OliveGreen}{x+x}\color{black}{+2}&=36 \\ 2x+2&=36 \\ 2x+2\color{Cerulean}{-2}&=36\color{Cerulean}{-2} \\ 2x&=34 \\ \frac{2x}{\color{Cerulean}{2}}&=\frac{34}{\color{Cerulean}{2}} \\ x&=17 \end{aligned}\)
Use \(x + 2\) to find the next odd integer.
\(x+2=\color{OliveGreen}{17}\color{black}{+2=19}\)
Answer:
The consecutive odd integers are \(17\) and \(19\).
The algebraic setup for even and odd integer problems is the same. A common mistake is to use \(x\) and \(x + 3\) when identifying the variables for consecutive odd integers. This is incorrect because adding 3 to an odd number yields an even number: for example, \(5 + 3 = 8\). An incorrect setup is very likely to lead to a decimal answer, which may be an indication that the problem was set up incorrectly.
The sum of three consecutive integers is \(24\). Find the integers.
Solution:
Consecutive integers are separated by one unit.
Let \(x\) represent the first integer.
Let \(x+1\) represent the next integer.
Let \(x+2\) represent the third integer.
Add the integers and set the sum equal to \(24\).
\(x+(x+1)+(x+2)=24\)
Solve.
\(\begin{aligned} \color{OliveGreen}{x+x}\color{black}{+1}\color{OliveGreen}{+x}\color{black}{+2}&=24\\ 3x+3&=24 \\ 3x+3\color{Cerulean}{-3}&=24\color{Cerulean}{-3} \\ 3x&=21 \\ x&=7 \end{aligned}\)
Back substitute to find the other two integers.
\(x+1=\color{OliveGreen}{7}\color{black}{+1=8}\)
\(x+2=\color{OliveGreen}{7}\color{black}{+2=9}\)
Answer:
The three consecutive integers are \(7, 8\) and \(9\), where \(7 + 8 + 9 = 24\).
The sum of three consecutive odd integers is \(87\). Find the integers.
- Answer
-
The integers are \(27, 29\), and \(31\).
Geometry Problems (Perimeter)
Recall that the perimeter of a polygon is the sum of the lengths of all the outside edges. In addition, it is helpful to review the following perimeter formulas \((π≈3.14159)\).
| Perimeter of a rectangle: | \(P=2l+2w\) |
| Perimeter of a square: | \(P=4s\) |
| Perimeter of a triangle: | \(P=a+b+c\) |
| Perimeter of a circle (circumference): | \(C=2\pi r\) |
Keep in mind that you are looking for a relationship between the unknowns so that you can set up algebraic equations using only one variable. When working with geometry problems, it is often helpful to draw a picture.
A rectangle has a perimeter measuring \(64\) feet. The length is \(4\) feet more than \(3\) times the width. Find the dimensions of the rectangle.
Solution:
The sentence “The length is 4 feet more than 3 times the width” gives the relationship between the two variables.
.png?revision=1)
Figure \(\PageIndex{4}\)
Let \(w\) represent the width of the rectangle.
Let \(3w+4\) represent the length.
The sentence “A rectangle has a perimeter measuring \(64\) feet” suggests an algebraic setup. Substitute \(64\) for the perimeter and the expression for the length into the appropriate formula as follows:
\(\begin{aligned} P&=\:\:\:\:\quad 2l + 2w \\ \color{Cerulean}{\downarrow}&\:\:\:\qquad\quad\color{Cerulean}{\downarrow} \\ \color{OliveGreen}{64}&=2(\color{OliveGreen}{3w+4}\color{black}{)+2w} \end{aligned}\)
Once you have set up an algebraic equation with one variable, solve for the width, \(w\).
\(\begin{aligned} 64&=\color{OliveGreen}{6w}\color{black}{+8+}\color{OliveGreen}{2w} \\ 64&=8w+8 \\ 64\color{Cerulean}{-8}&=8w+8\color{Cerulean}{-8} \\ 56&=8w \\ \frac{56}{\color{Cerulean}{8}}&=\frac{8w}{\color{Cerulean}{8}} \\ 7&=w \end{aligned}\)
Use \(3w + 4\) to find the length.
\(l=3w+4=3(\color{OliveGreen}{7}\color{black}{)+4=21+4=25}\)
Answer:
The rectangle measures \(7\) feet by \(25\) feet. To check, add all of the sides:
\(P=7\text{ ft+}7\text{ ft+}25\text{ ft+}25\text{ ft}=64\text{ ft}\)
Two sides of a triangle are \(5\) and \(7\) inches longer than the third side. If the perimeter measures \(21\) inches, find the length of each side.
.png?revision=1)
Figure \(\PageIndex{5}\)
Solution:
The first sentence describes the relationships between the unknowns.
Let \(x\) represent the length of the third side.
Let \(x+5\) and \(x+7\) represent the lengths of the other two sides.
Substitute these expressions into the appropriate formula and use \(21\) for the perimeter \(P\).
\(\begin{aligned} P&=a+b+c \\ \color{OliveGreen}{21}&=\color{OliveGreen}{x}\color{black}{+}\color{OliveGreen}{(x+5)}\color{black}{+}\color{OliveGreen}{(x+7)} \end{aligned}\)
You now have an equation with one variable to solve.
\(\begin{aligned} 21&=x+x+5+x+7 \\ 21&=3x+12 \\ 21\color{Cerulean}{-12}&=3x+12\color{Cerulean}{-12} \\ 9&=3x\\ \frac{9}{\color{Cerulean}{3}}&=\frac{3x}{\color{Cerulean}{3}} \\ 3&=x \end{aligned}\)
Back substitute.
\(x+5=\color{OliveGreen}{3}\color{black}{+5=8}\)
\(x+5=\color{OliveGreen}{3}\color{black}{+7=10}\)
Answer:
The three sides of the triangle measure \(3\) inches, \(8\) inches, and \(10\) inches. The check is left to the reader.
The length of a rectangle is \(1\) foot less than twice its width. If the perimeter is \(46\) feet, find the dimensions.
- Answer
-
Width: \(8\) feet; length: \(15\) feet
Problems Involving Money and Percents
Whenever setting up an equation involving a percentage, we usually need to convert the percentage to a decimal or fraction. If the question asks for a percentage, then do not forget to convert your answer to a percent at the end. Also, when money is involved, be sure to round off to two decimal places.
If a pair of shoes costs $\(52.50\) including a \(7\frac{1}{4}\)% tax, what is the original cost of the item before taxes are added?
Solution:
Begin by converting \(7\frac{1}{4}\)% to a decimal.
\(7\frac{1}{4}%=7.25%=0.0725\)
The amount of tax is this rate times the original cost of the item. The original cost of the item is what you are asked to find.
Let \(c\) represent the cost of the item \(\underline{\text{before taxes}}\) are added.
\(\color{Cerulean}{amount\:of\:tax\:=\:tax\:rate\:\cdot\:cost\:of\:item}\)
\(=0.0725\cdot c\)
\(\color{Cerulean}{total\:cost\:=\:cost\:of\:item\:+\:amount\:of\:tax}\)
\(52.50=c+0.0725c\)
Use this equation to solve for \(c\), the original cost of the item.
\(\begin{aligned} 52.50&=\color{OliveGreen}{1c+0.0725c} \\ 52.50&=1.0725c \\ \frac{52.50}{\color{Cerulean}{1.0725}}&=\frac{1.0725c}{\color{Cerulean}{1.0725}} \\ 48.95& \approx c \end{aligned}\)
Answer:
The cost of the item before taxes is $\(48.95\). Check this by multiplying $\(48.95\) by \(0.0725\) to obtain the tax and add it to this cost.
Given a \(5\frac{1}{8}\)% annual interest rate, how long will it take $\(1,200\) to yield $\(307.50\) in simple interest?
Solution:
Let \(t\) represent the time needed to earn $\(307.50\) at \(5.125\)%.
Organize the data needed to use the simple interest formula \(I=prt\).
| Given interest for the time period: | \(I=\)$\(307.50\) |
| Given principal: | \(p=\)$\(1200\) |
| Given rate: | \(r=5\frac{1}{8}\)%\(=5.125\)%\(=0.05125\) |
Next, substitute all of the known quantities into the formula and then solve for the only unknown, \(t\).
\(\begin{aligned} I&=prt \\ \color{OliveGreen}{307.50}&=\color{OliveGreen}{1200}\color{black}{(}\color{OliveGreen}{0.05125}\color{black}{)t} \\ 307.50&=61.5t \\ \frac{307.50}{\color{Cerulean}{61.5}}&=\frac{61.5t}{\color{Cerulean}{61.5}} \\ 5&=t \end{aligned}\)
Answer:
It takes \(5\) years for $\(1,200\) invested at \(5\frac{1}{8}\)% to earn $\(307.50\) in simple interest.
Mary invested her total savings of $\(3,400\) in two accounts. Her mutual fund account earned \(8\)% last year and her CD earned \(5\)%. If her total interest for the year was $\(245\), how much was in each account?
Solution:
The relationship between the two unknowns is that they total $3,400. When a total is involved, a common technique used to avoid two variables is to represent the second unknown as the difference of the total and the first unknown.
Let \(x\) represent the amount invested in the mutual fund at \(8\)%\(=0.08\).
Let \(3,400-x\) represent the remaining amount invested in the CD at \(5\)%\(=0.05\).
The total interest is the sum of the interest earned from each account.
| Interest earned in the mutual fund: | \(I=Prt=x⋅0.08⋅1=0.08x\) |
| Interest earned in the CD: | \(I=Prt=(3,400−x)⋅0.05⋅1=0.05(3,400−x)\) |
\(\color{Cerulean}{mutual\:fund\:interest\:+\:CD\:interest\:=\:total\:interest}\)
\(0.08x+0.05(3,400-x)=245\)
This equation models the problem with one variable. Solve for \(x\).
\(\begin{aligned} 0.08x+0.05(3,400-x)&=245 \\ \color{OliveGreen}{0.08x}\color{black}{+170}\color{OliveGreen}{-0.05x}&=245 \\ 0.03x+170\color{Cerulean}{-170} &=245\color{Cerulean}{-170} \\ 0.03x&=75 \\ \frac{0.03x}{\color{Cerulean}{0.03}}&=\frac{75}{\color{Cerulean}{0.03}} \\ x&=2,500 \end{aligned}\)
Back substitute.
\(3,400-x=3,400-\color{OliveGreen}{2,500}\color{black}{=900}\)
Answer:
Mary invested $\(2,500\) at \(8\)% in a mutual fund and $\(900\) at \(5\)% in a CD.
Joe has a handful of dimes and quarters that values $\(5.30\). He has one fewer than twice as many dimes than quarters. How many of each coin does he have?
Solution:
Begin by identifying the variables.
Let \(q\) represent the number of quarters Joe is holding.
Let \(2q-1\) represent the number of dimes.
To determine the total value of a number of coins, multiply the number of coins by the value of each coin. For example, \(5\) quarters have a value $\(0.25 ⋅ 5 =\) $\(1.25\).
\(\color{Cerulean}{value\:in\:quarters\:+\:value\:in\:dimes\:=\:total\:value\:of\:coins}\)
\(0.25q+0.10(2q-1)=5.30\)
Solve for the number of quarters, \(q\).
\(\begin{aligned} 0.25q+0.10(2q-1)&=5.30 \\ \color{OliveGreen}{0.25q+0.20q}\color{black}{-0.10}&=5.30 \\ 0.45q-0.10&=5.30 \\ 0.45q-0.10\color{Cerulean}{+0.10}&=5.30\color{Cerulean}{+0.10} \\ 0.45q&=5.40 \\ \frac{0.45q}{\color{Cerulean}{0.45}}&=\frac{5.40}{\color{Cerulean}{0.45}} \\ q&=12 \end{aligned}\)
Back substitute into \(2q − 1\) to find the number of dimes.
\(2q-1=2(\color{OliveGreen}{12}\color{black}{)-1=24-1=23}\)
Answer:
Joe has \(12\) quarters and \(23\) dimes. Check by multiplying $\(0.25 ⋅ 12 = \)$\(3.00\) and $\(0.10 ⋅ 23 = \)$\(2.30\). Then add to obtain the correct amount: $\(3.00 + \)$\(2.30 = \)$\(5.30\).
A total amount of $\(5,900\) is invested in two accounts. One account earns \(3.5\)% interest and another earns \(4.5\)%. If the interest for \(1\) year is $\(229.50\), then how much is invested in each account?
- Answer
-
$\(3,600\) is invested at \(3.5\)% and $\(2,300\) at \(4.5\)%.
Uniform Motion Problems (Distance Problems)
Uniform motion refers to movement at a speed, or rate that does not change. We can determine the distance traveled by multiplying the average rate by the time traveled at that rate with the formula \(D=r⋅t\). Applications involving uniform motion usually have a lot of data, so it helps to first organize the data in a chart and then set up an algebraic equation that models the problem.
Two trains leave the station at the same time traveling in opposite directions. One travels at \(70\) miles per hour and the other at \(60\) miles per hour. How long does it take for the distance between them to reach \(390\) miles?
Solution:
First, identify the unknown quantity and organize the data.
Let \(t\) represent the time it takes to separate \(390\) miles.
.png?revision=1)
Figure \(\PageIndex{6}\)
The given information is filled in on the following chart. The time for each train is equal.
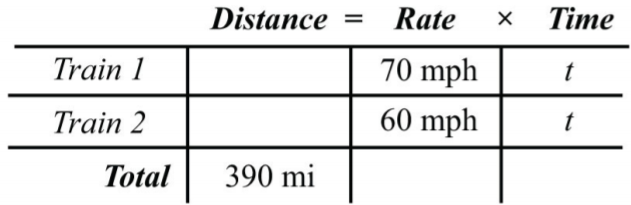.png?revision=1)
Figure \(\PageIndex{7}\)
To avoid introducing two more variables, use the formula \(D=r⋅t\) to fill in the unknown distances traveled by each train.
Distance traveled by train 1: \(D=r\cdot t=70\cdot t\)
Distance traveled by tain 2: \(D=r\cdot t=60\cdot t\)
We can now completely fill in the chart.
.png?revision=1)
Figure \(\PageIndex{8}\)
The algebraic setup is defined by the distance column. The problem asks for the time it takes for the total distance to reach \(390\) miles.
.png?revision=1)
Figure \(\PageIndex{9}\)
Solve for \(t\).
\(\begin{aligned} 70t+60t&=390 \\ 130t&=390 \\ \frac{130t}{\color{Cerulean}{130}}&=\frac{390}{\color{Cerulean}{130}} \\ t&=3 \end{aligned}\)
Answer:
It takes \(3\) hours for the distance between the trains to reach \(390\) miles.
A train traveling nonstop to its destination is able to make the trip at an average speed of \(72\) miles per hour. On the return trip, the train makes several stops and is only able to average \(48\) miles per hour. If the return trip takes \(2\) hours longer than the initial trip to the destination, then what is the travel time each way?
Solution:
First, identify the unknown quantity and organize the data.
Let \(t\) represent the time it takes to arrive at the destination.
Let \(t+2\) represent the time it takes for the return trip.
.png?revision=1)
Figure \(\PageIndex{10}\)
The given information is filled in the following chart:
.png?revision=1)
Figure \(\PageIndex{11}\)
Use the formula \(D=r⋅t\) to fill in the unknown distances.
Distance traveled on the destination: \(D=r\cdot t=72\cdot t\)
Distance traveled on the return trip: \(D=r\cdot t=48\cdot (t+2)\)
Use these expressions to complete the chart.
.png?revision=1)
Figure \(\PageIndex{12}\)
The algebraic setup is again defined by the distance column. In this case, the distance to the destination and back is the same, and the equation is
\(72t=48(t+2)\)
Solve for \(t\).
\(\begin{aligned} 72t&=48(t+2) \\ 722&=48t+96 \\ 72t-48t&=48t+96-48t \\ 24t&=96 \\ \frac{24t}{24}&=\frac{96}{24} \\ t&=4 \end{aligned}\)
The return trip takes \(t+2=4+2=6\) hours.
Answer:
It takes \(4\) hours to arrive at the destination and \(6\) hours to return.
Mary departs for school on a bicycle at an average rate of \(6\) miles per hour. Her sister Kate, running late, leaves \(15\) minutes later and cycles at twice that speed. How long will it take Kate to catch up to Mary? Be careful! Pay attention to the units given in the problem.
- Answer
-
It takes \(15\) minutes for Kate to catch up.
Key Takeaways
- Simplify the process of solving real-world problems by creating mathematical models that describe the relationship between unknowns. Use algebra to solve the resulting equations.
- Guessing and checking for solutions is a poor practice. This technique might sometimes produce correct answers, but is unreliable, especially when problems become more complex.
- Read the problem several times and search for the key words and phrases. Identify the unknowns and assign variables or expressions to the unknown quantities. Look for relationships that allow you to use only one variable. Set up a mathematical model for the situation and use algebra to solve the equation. Check to see if the solution makes sense and present the solution in sentence form.
- Do not avoid word problems: solving them can be fun and rewarding. With lots of practice you will find that they really are not so bad after all. Modeling and solving applications is one of the major reasons to study algebra.
- Do not feel discouraged when the first attempt to solve a word problem does not work. This is part of the process. Try something different and learn from incorrect attempts.
Translate the following into algebraic equations.
- The sum of a number and \(6\) is \(37\).
- When \(12\) is subtracted from twice some number the result is \(6\).
- Fourteen less than \(5\) times a number is \(1\).
- Twice some number is subtracted from \(30\) and the result is \(50\).
- Five times the sum of \(6\) and some number is \(20\).
- The sum of \(5\) times some number and \(6\) is \(20\).
- When the sum of a number and \(3\) is subtracted from \(10\) the result is \(5\).
- The sum of three times a number and five times that same number is \(24\).
- Ten is subtracted from twice some number and the result is the sum of the number and \(2\).
- Six less than some number is ten times the sum of that number and \(5\).
- Answer
-
1. \(x+6=37\)
3. \(5x−14=1\)
5. \(5(x+6)=20\)
7. \(10−(x+3)=5\)
9. \(2x−10=x+2\)
Set up an algebraic equation and then solve.
- A larger integer is \(1\) more than twice another integer. If the sum of the integers is \(25\), find the integers.
- If a larger integer is \(2\) more than \(4\) times another integer and their difference is \(32\), find the integers.
- One integer is \(30\) more than another integer. If the difference between the larger and twice the smaller is \(8\), find the integers.
- The quotient of some number and \(4\) is \(22\). Find the number.
- Eight times a number is decreased by three times the same number, giving a difference of \(20\). What is the number?
- One integer is two units less than another. If their sum is \(−22\), find the two integers.
- The sum of two consecutive integers is \(139\). Find the integers.
- The sum of three consecutive integers is \(63\). Find the integers.
- The sum of three consecutive integers is \(279\). Find the integers.
- The difference of twice the smaller of two consecutive integers and the larger is \(39\). Find the integers.
- If the smaller of two consecutive integers is subtracted from two times the larger, then the result is \(17\). Find the integers.
- The sum of two consecutive even integers is \(46\). Find the integers.
- The sum of two consecutive even integers is \(238\). Find the integers.
- The sum of three consecutive even integers is \(96\). Find the integers.
- If the smaller of two consecutive even integers is subtracted from \(3\) times the larger the result is \(42\). Find the integers.
- The sum of three consecutive even integers is \(90\). Find the integers.
- The sum of two consecutive odd integers is \(68\). Find the integers.
- The sum of two consecutive odd integers is \(180\). Find the integers.
- The sum of three consecutive odd integers is \(57\). Find the integers.
- If the smaller of two consecutive odd integers is subtracted from twice the larger the result is \(23\). Find the integers.
- Twice the sum of two consecutive odd integers is \(32\). Find the integers.
- The difference between twice the larger of two consecutive odd integers and the smaller is \(59\). Find the integers.
- Answer
-
1. \(8, 17\)
3. \(22, 52\)
5. \(4\)
7. \(69, 70\)
9. \(92, 93, 94\)
11. \(15, 16\)
13. \(118, 120\)
15. \(18, 20\)
17. \(33, 35\)
19. \(17, 19, 21\)
21. \(7, 9\)
Set up an algebraic equation and then solve.
- If the perimeter of a square is \(48\) inches, then find the length of each side.
- The length of a rectangle is \(2\) inches longer than its width. If the perimeter is \(36\) inches, find the length and width.
- The length of a rectangle is \(2\) feet less than twice its width. If the perimeter is \(26\) feet, find the length and width.
- The width of a rectangle is \(2\) centimeters less than one-half its length. If the perimeter is \(56\) centimeters, find the length and width.
- The length of a rectangle is \(3\) feet less than twice its width. If the perimeter is \(54\) feet, find the dimensions of the rectangle.
- If the length of a rectangle is twice as long as the width and its perimeter measures \(72\) inches, find the dimensions of the rectangle.
- The perimeter of an equilateral triangle measures \(63\) centimeters. Find the length of each side.
- An isosceles triangle whose base is one-half as long as the other two equal sides has a perimeter of \(25\) centimeters. Find the length of each side.
- Each of the two equal legs of an isosceles triangle are twice the length of the base. If the perimeter is \(105\) centimeters, then how long is each leg?
- A triangle has sides whose measures are consecutive even integers. If the perimeter is \(42\) inches, find the measure of each side.
- A triangle has sides whose measures are consecutive odd integers. If the perimeter is \(21\) inches, find the measure of each side.
- A triangle has sides whose measures are consecutive integers. If the perimeter is \(102\) inches, then find the measure of each side.
- The circumference of a circle measures \(50π\) units. Find the radius.
- The circumference of a circle measures \(10π\) units. Find the radius.
- The circumference of a circle measures \(100\) centimeters. Determine the radius to the nearest tenth.
- The circumference of a circle measures \(20\) centimeters. Find the diameter rounded off to the nearest hundredth.
- The diameter of a circle measures \(5\) inches. Determine the circumference to the nearest tenth.
- The diameter of a circle is \(13\) feet. Calculate the exact value of the circumference.
- Answer
-
1. \(12\) inches
3. Width: \(5\) feet; length: \(8\) feet
5. Width: \(10\) feet; length: \(17\) feet
7. \(21\) centimeters
9. \(21\) centimeters, \(42\) centimeters, \(42\) centimeters
11. \(5\) inches, \(7\) inches, \(9\) inches
13. \(25\) units
15. \(15.9\) centimeters
17. \(15.7\) inches
Set up an algebraic equation and then solve.
- Calculate the simple interest earned on a \(2\)-year investment of $\(1,550\) at a \(8\frac{3}{4}\)% annual interest rate.
- Calculate the simple interest earned on a \(1\)-year investment of $\(500\) at a \(6\)% annual interest rate.
- For how many years must $\(10,000\) be invested at an \(8\frac{1}{2}\)% annual interest rate to yield $\(4,250\) in simple interest?
- For how many years must $\(1,000\) be invested at a \(7.75\)% annual interest rate to yield $\(503.75\) in simple interest?
- At what annual interest rate must $\(2,500\) be invested for \(3\) years in order to yield $\(412.50\) in simple interest?
- At what annual interest rate must $\(500\) be invested for \(2\) years in order to yield $\(93.50\) in simple interest?
- If the simple interest earned for \(1\) year was $\(47.25\) and the annual rate was \(6.3\)%, what was the principal?
- If the simple interest earned for \(2\) years was $\(369.60\) and the annual rate was \(5\frac{1}{4}\)%, what was the principal?
- Joe invested last year’s $\(2,500\) tax return in two different accounts. He put most of the money in a money market account earning \(5\)% simple interest. He invested the rest in a CD earning \(8\)% simple interest. How much did he put in each account if the total interest for the year was $\(138.50\)?
- James invested $\(1,600\) in two accounts. One account earns \(4.25\)% simple interest and the other earns \(8.5\)%. If the interest after \(1\) year was $\(85\), how much did he invest in each account?
- Jane has her $\(5,400\) savings invested in two accounts. She has part of it in a CD at \(3\)% annual interest and the rest in a savings account that earns \(2\)% annual interest. If the simple interest earned from both accounts is $\(140\) for the year, then how much does she have in each account?
- Marty put last year’s bonus of $\(2,400\) into two accounts. He invested part in a CD with \(2.5\)% annual interest and the rest in a money market fund with \(1.3\)% annual interest. His total interest for the year was $\(42.00\). How much did he invest in each account?
- Alice puts money into two accounts, one with \(2\)% annual interest and another with \(3\)% annual interest. She invests \(3\) times as much in the higher yielding account as she does in the lower yielding account. If her total interest for the year is $\(27.50\), how much did she invest in each account?
- Jim invested an inheritance in two separate banks. One bank offered \(5.5\)% annual interest rate and the other \(6\frac{1}{4}\)%. He invested twice as much in the higher yielding bank account than he did in the other. If his total simple interest for \(1\) year was $\(4,860\), then what was the amount of his inheritance?
- If an item is advertised to cost $\(29.99\) plus \(9.25\)% tax, what is the total cost?
- If an item is advertised to cost $\(32.98\) plus \(8\frac{3}{4}\)% tax, what is the total cost?
- An item, including an \(8.75\)% tax, cost $\(46.49\). What is the original pretax cost of the item?
- An item, including a \(5.48\)% tax, cost $\(17.82\). What is the original pretax cost of the item?
- If a meal costs $\(32.75\), what is the total after adding a \(15\)% tip?
- How much is a \(15\)% tip on a restaurant bill that totals $\(33.33\)?
- Ray has a handful of dimes and nickels valuing $\(3.05\). He has \(5\) more dimes than he does nickels. How many of each coin does he have?
- Jill has \(3\) fewer half-dollars than she has quarters. The value of all \(27\) of her coins adds to $\(9.75\). How many of each coin does Jill have?
- Cathy has to deposit $\(410\) worth of five- and ten-dollar bills. She has \(1\) fewer than three times as many tens as she does five-dollar bills. How many of each bill does she have to deposit?
- Billy has a pile of quarters, dimes, and nickels that values $\(3.75\). He has \(3\) more dimes than quarters and \(5\) more nickels than quarters. How many of each coin does Billy have?
- Mary has a jar with one-dollar bills, half-dollar coins, and quarters valuing $\(14.00\). She has twice as many quarters than she does half-dollar coins and the same amount of half-dollar coins as one-dollar bills. How many of each does she have?
- Chad has a bill-fold of one-, five-, and ten-dollar bills totaling $\(118\). He has \(2\) more than \(3\) times as many ones as he does five-dollar bills and \(1\) fewer ten- than five-dollar bills. How many of each bill does Chad have?
- Answer
-
1. $\(271.25\)
3. \(5\) years
5. \(5.5\)%
7. $\(750.00\)
9. Joe invested $\(2,050\) in the money market account and $\(450\) in the CD.
11. Jane has $\(3,200\) in the CD and $\(2,200\) in savings.
13. Alice invested $\(250\) at \(2\)% and $\(750\) at a \(3\)%.
15. $\(32.76\)
17. $\(42.75\)
19. $\(37.66\)
21. He has \(17\) nickels and \(22\) dimes.
23. Cathy has \(12\) fives and \(35\) ten-dollar bills.
25. Mary has \(7\) one-dollar bills, \(7\) half-dollar coins, and \(14\) quarters.
Set up an algebraic equation then solve.
- Two cars leave a location traveling in opposite directions. If one car averages \(55\) miles per hour and the other averages \(65\) miles per hour, then how long will it take for them to separate a distance of \(300\) miles?
- Two planes leave the airport at the same time traveling in opposite directions. The average speeds for the planes are \(450\) miles per hour and \(395\) miles per hour. How long will it take the planes to be a distance of \(1,478.75\) miles apart?
- Bill and Ted are racing across the country. Bill leaves \(1\) hour earlier than Ted and travels at an average rate of \(60\) miles per hour. If Ted intends to catch up at a rate of \(70\) miles per hour, then how long will it take?
- Two brothers leave from the same location, one in a car and the other on a bicycle, to meet up at their grandmother’s house for dinner. If one brother averages \(30\) miles per hour in the car and the other averages \(12\) miles per hour on the bicycle, then it takes the brother on the bicycle \(1\) hour less than \(3\) times as long as the other in the car. How long does it take each of them to make the trip?
- A commercial airline pilot flew at an average speed of \(350\) miles per hour before being informed that his destination airfield may be closed due to poor weather conditions. In an attempt to arrive before the storm, he increased his speed \(400\) miles per hour and flew for another \(3\) hours. If the total distance flown was \(2,950\) miles, then how long did the trip take?
- Two brothers drove the \(2,793\) miles from Los Angeles to New York. One of the brothers, driving during the day, was able to average \(70\) miles per hour, and the other, driving at night, was able to average \(53\) miles per hour. If the brother driving at night drove \(3\) hours less than the brother driving in the day, then how many hours did they each drive?
- Joe and Ellen live \(21\) miles apart. Departing at the same time, they cycle toward each other. If Joe averages \(8\) miles per hour and Ellen averages \(6\) miles per hour, how long will it take them to meet?
- If it takes \(6\) minutes to drive to the automobile repair shop at an average speed of \(30\) miles per hour, then how long will it take to walk back at an average rate of \(4\) miles per hour?
- Jaime and Alex leave the same location and travel in opposite directions. Traffic conditions enabled Alex to average \(14\) miles per hour faster than Jaime. After \(1\frac{1}{2}\) hours they are \(159\) miles apart. Find the speed at which each was able to travel.
- Jane and Holly live \(51\) miles apart and leave at the same time traveling toward each other to meet for lunch. Jane traveled on the freeway at twice the average speed as Holly. They were able to meet in a half hour. At what rate did each travel?
- Answer
-
1. \(2.5\) hours
3. \(6\) hours
5. \(8\) hours
7. \(1\frac{1}{2}\) hours
9. Jaime: \(46\) miles per hour; Alex: \(60\) miles per hour
- Discuss ideas for calculating taxes and tips mentally.
- Research historical methods for representing unknowns.
- Research and compare simple interest and compound interest. What is the difference?
- Discuss why algebra is a required subject.
- Research ways to show that a repeating decimal is rational. Share your findings on the discussion board.
- Answer
-
1. Answers may vary
3. Answers may vary
5. Answers may vary


