2.8: Linear Inequalities (One Variable)
- Page ID
- 24430
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify linear inequalities and check solutions.
- Solve linear inequalities and express the solutions graphically on a number line and in interval notation.
- Solve compound linear inequalities and express the solutions graphically on a number line and in interval notation.
- Solve applications involving linear inequalities and interpret the results.
Definition of a Linear Inequality
A linear inequality is a mathematical statement that relates a linear expression as either less than or greater than another. The following are some examples of linear inequalities, all of which are solved in this section:
\(3x+7<16\quad -2x+1\geq 21\quad -7(2x+1)<1\)
A solution to a linear inequality is a real number that will produce a true statement when substituted for the variable. Linear inequalities have either infinitely many solutions or no solution. If there are infinitely many solutions, graph the solution set on a number line and/or express the solution using interval notation.
Are \(x=−2\) and \(x=4\) solutions to \(3x+7<16\)?
Solution:
Substitute the values for \(x\), simplify, and check to see if we obtain a true statement.
\(\begin{array}{c|c} {\underline{Check\:x=-2}}&{\underline{Check\:x=4}}\\{\begin{aligned} 3(\color{OliveGreen}{-2}\color{black}{)+7}&<16 \\ -6+7&<16 \\ 1&<16\quad\color{Cerulean}{\checkmark} \end{aligned}}&{\begin{aligned} 3(\color{OliveGreen}{4}\color{black}{)+7}&<16 \\ 12+7&<16 \\ 19&<16\quad\color{red}{x} \end{aligned}} \end{array}\)
Answer:
\(x=-2\) is a solution and \(x=4\) is not.
Algebra of Linear Inequalities
All but one of the techniques learned for solving linear equations apply to solving linear inequalities. You may add or subtract any real number to both sides of an inequality, and you may multiply or divide both sides by any positive real number to create equivalent inequalities. For example,
-5\color{Cerulean}{-7} &\color{Cerulean}{Subtract\:7\:from\:both\:sides.} \\ 3&>-12\quad\color{Cerulean}{\checkmark} &\color{Cerulean}{True} \\ 10&>-5 \\ \frac{10}{\color{Cerulean}{5}}&>\frac{-5}{\color{Cerulean}{5}} &\color{Cerulean}{Divide\:both\:sides\:by\:5.} \\ 2&>-1\quad\color{Cerulean}{\checkmark} &\color{Cerulean}{True} \end{aligned}\)
Both subtracting \(7\) from each side and dividing each side by \(+5\) results in an equivalent inequality that is true.
Example \(\PageIndex{2}\)
Solve and graph the solution set:
\(3x+7<16\).
Solution:
\(\begin{aligned} 3x+7&<16 \\ 3x+7\color{Cerulean}{-7}&<16\color{Cerulean}{-7} \\ 3x&<9 \\ \frac{3x}{\color{Cerulean}{3}}&<\frac{9}{\color{Cerulean}{3}} \\ x&<3 \end{aligned}\)
.png?revision=1)
Figure \(\PageIndex{1}\)
It is helpful to take a minute and choose a few values in and out of the solution set, substitute them into the original inequality, and then verify the results. As indicated, you should expect \(x=0\) to solve the original inequality, but \(x=5\) should not.
\(\begin{array}{c|c} {\underline{Check\:x=0}}&{\underline{Check\:x=5}}\\{\begin{aligned} 3(\color{OliveGreen}{0}\color{black}{)+7}&<16 \\ 7&<16\quad\color{Cerulean}{\checkmark} \end{aligned}}&{\begin{aligned} 3(\color{OliveGreen}{5}\color{black}{)+7}&<16 \\ 15+7&<16 \\ 22&<16\quad\color{red}{x} \end{aligned}} \end{array}\)
Checking in this manner gives a good indication that the inequality is solved correctly. This can be done mentally.
Answer:
Interval notation: \((−∞, 3)\)
When working with linear inequalities, a different rule applies when multiplying or dividing by a negative number. To illustrate the problem, consider the true statement \(10>−5\) and divide both sides by \(−5\).
\frac{-5}{\color{Cerulean}{-5}} &\color{Cerulean}{Divide\:both\:sides\:by\:-5.} \\ -2&\color{red}{>}\color{black}{1}\quad\color{red}{x} &\color{Cerulean}{False} \end{aligned}\)
Dividing by \(−5\) results in a false statement. To retain a true statement, the inequality must be reversed.
\(\begin{aligned} 10&\color{OliveGreen}{>}\color{black}{-5} \\ \frac{10}{\color{Cerulean}{-5}}&<\frac{-5}{\color{Cerulean}{-5}} &\color{Cerulean}{Reverse\:the\:inequality.} \\ -2&\color{OliveGreen}{<}\color{black}{1}\quad\color{Cerulean}{\checkmark}&\color{Cerulean}{True} \end{aligned}\)
The same problem occurs when multiplying by a negative number. This leads to the following new rule: when multiplying or dividing by a negative number, reverse the inequality. It is easy to forget to do this so take special care to watch for negative coefficients.
In general, given algebraic expressions \(A\) and \(B\), where \(c\) is a positive nonzero real number, we have the following properties of inequalities:
\(\begin{array}{ll}{\textbf{Addition property of inequalities:}}&{\text{If }A<B\text{ then, }A\color{Cerulean}{+c}\color{black}{<B}\color{Cerulean}{+c}}\\{\textbf{Subtraction property of inequalities:}}&{\text{If }A<B,\text{ then }A\color{Cerulean}{-c}\color{black}{<B}\color{Cerulean}{-c}}\\{\textbf{Multiplication property of inequalities:}}&{\text{If }A<B,\text{ then }\color{Cerulean}{c}\color{black}{A<}\color{Cerulean}{c}\color{black}{B}}\\{}&{\text{If }A<B,\text{ then }\color{Cerulean}{-c}\color{black}{A}\color{OliveGreen}{>}\color{Cerulean}{-c}\color{black}{B}}\\{\textbf{Division property of inequalities:}}&{\text{If }A<B,\text{ then }\frac{A}{\color{Cerulean}{c}}\color{black}{<\frac{B}{\color{Cerulean}{c}}}}\\{}&{\text{If }A<B,\text{ then }\frac{A}{\color{Cerulean}{-c}}\color{OliveGreen}{>}\color{black}{\frac{B}{\color{Cerulean}{-c}}}} \end{array}\)
We use these properties to obtain an equivalent inequality, one with the same solution set, where the variable is isolated. The process is similar to solving linear equations.
Solve:
\(−2x+1≥21\).
Solution:

Figure \(\PageIndex{2}\)
Answer:
Interval notation: \((−∞, −10]\)
Solve:
\(−7(2x+1)<1\).
Solution:
\(\begin{aligned} -7(2x+1)&<1 & & \color{Cerulean}{Distribute.} \\ -14x-7&<1 \\ -14x-7\color{Cerulean}{+7}&<1\color{Cerulean}{+7} \\ 14x&<8 \\ \frac{-14x}{\color{Cerulean}{-14}}&\color{OliveGreen}{>}\color{black}{\frac{8}{\color{Cerulean}{-14}}} & & \color{Cerulean}{Reverse\:the\:inequality.} \\ x&>-\color{black}{\frac{8\color{Cerulean}{\div 2}}{14\color{Cerulean}{\div 2}}} & & \color{Cerulean}{Reduce.} \\ x&>-\frac{4}{7} \end{aligned}\)
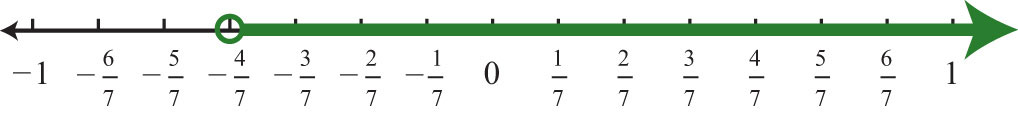
Figure \(\PageIndex{3}\)
Answer:
Interval notation: \((−\frac{4}{7}, ∞)\)
Solve:
\(5x−3(2x−1)≥2(x−3)\).
Solution:
.png?revision=1)
Figure \(\PageIndex{4}\)
Answer:
Interval notation: \((−∞, 3]\)
Solve:
\(3−5(x−1)≤28\).
- Answer
-
\([−4, ∞)\)
Compound Inequalities
Following are some examples of compound linear inequalities:
\(-3<2x+5<17\)
\(-1\leq\frac{1}{2}x-3<1\)
\(3x+1<10\quad or\quad 2x-1\geq 11\)
These compound inequalities are actually two inequalities in one statement joined by the word “and” or by the word “or.” For example,
\(-3<2x+5<17\)
is a compound inequality because it can be decomposed as follows:
\(-3<2x+5\quad\text{and}\quad 2x+5<17\)
Solve each inequality individually, and the intersection of the two solution sets solves the original compound inequality. While this method works, there is another method that usually requires fewer steps. Apply the properties of this section to all three parts of the compound inequality with the goal of isolating the variable in the middle of the statement to determine the bounds of the solution set.
Solve:
\(−3<2x+5<17\).
Solution:
\(\begin{array}{c} {-3<2x+5<17}\\{-3\color{Cerulean}{-5}\color{black}{<2x+5}\color{Cerulean}{-5}\color{black}{<17}\color{Cerulean}{-5}}\\{-8<2x<12}\\{\frac{-8}{\color{Cerulean}{2}}\color{black}{<\frac{2x}{\color{Cerulean}{2}}<\frac{12}{\color{Cerulean}{2}}}}\\{-4<x<6} \end{array}\)
.png?revision=1)
Figure \(\PageIndex{5}\)
Answer:
Interval notation: \((−4, 6)\)
Solve:
\(−1≤\frac{1}{2}x−3<1\).
Solution:
\(\begin{array}{c}{-1\leq\frac{1}{2}x-3<1}\\{-1\color{Cerulean}{+3}\color{black}{\leq\frac{1}{2}x-3}\color{Cerulean}{+3}\color{black}{<1}\color{Cerulean}{+3}}\\{2\leq\frac{1}{2}x<4}\\{\color{Cerulean}{2}\color{black}{\cdot 2\leq}\color{Cerulean}{2}\color{black}{\cdot\frac{1}{2}x<}\color{Cerulean}{2}\color{black}{\cdot 4}}\\{4\leq x<8} \end{array}\)
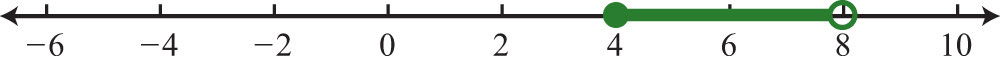
Figure \(\PageIndex{6}\)
Answer:
Interval notation: \([4, 8)\)
It is important to note that when multiplying or dividing all three parts of a compound inequality by a negative number, you must reverse all of the inequalities in the statement. For example,
\(\begin{array}{c}{-10<-2x<20}\\{\frac{-10}{\color{Cerulean}{-2}}\color{OliveGreen}{>}\color{black}{\frac{-2x}{\color{Cerulean}{-2}}}\color{OliveGreen}{>}\color{black}{\frac{20}{\color{Cerulean}{-2}}}}\\{5>x>-10} \end{array}\)
The answer above can be written in an equivalent form, where smaller numbers lie to the left and the larger numbers lie to the right, as they appear on a number line.
\(-10<x<5\)
Using interval notation, write \((−10, 5)\).
Solve:
\(−8≤2(−3x+5)<34\).
- Answer
-
\((−4, 3]\)
For compound inequalities with the word “or” you must work both inequalities separately and then consider the union of the solution sets. Values in this union solve either inequality.
Solve:
\(3x+1<10\) or \(2x−1≥11\).
Solution:
Solve each inequality and form the union by combining the solution sets.
\(\begin{array}{ccc}{3x+1<10}&{}&{2x-1\geq 11}\\{3x+1\color{Cerulean}{-1}\color{black}{<10}\color{Cerulean}{-1}}&{}&{2x-1\color{Cerulean}{+1}\color{black}{\geq 11}\color{Cerulean}{+1}}\\{3x<9}&{\text{or}}&{2x\geq 12}\\{\frac{3x}{\color{Cerulean}{3}}\color{black}{<\frac{9}{\color{Cerulean}{3}}}}&{}&{\frac{2x}{\color{Cerulean}{2}}\color{black}{\geq \frac{12}{\color{Cerulean}{2}}}}\\{x<3}&{}&{x\geq 6} \end{array}\)

Figure \(\PageIndex{7}\)
Answer:
Interval notation: \((−∞, 3)∪[6, ∞)\)
Solve:
\(4x−1<-5\) or \(4x-1>5\).
- Answer
-
\((−∞,−1)∪(\frac{3}{2}, ∞)\)
Applications of Linear Inequalities
Some of the key words and phrases that indicate inequalities are summarized below:
| Key Phrases | Translation |
|---|---|
| A number is at least \(5\). |
\(x\geq 5\) |
| A number is \(5\) or more inclusive. | |
| A number is at most \(3\). |
\(x\leq 3\) |
| A number is \(3\) or less inclusive. | |
| A number is strictly less than \(4\). |
\(x<4\) |
| A number is less than \(4\), noninclusive. | |
| A number is greater than \(7\). |
\(x>7\) |
| A number is more than \(7\), noninclusive. | |
| A number is in between \(2\) and \(10\). | \(2<x<10\) |
| A number is at least \(5\) and at most \(15\). |
\(5\leq x\leq 15\) |
| A number may range from \(5\) to \(15\). |
As with all applications, carefully read the problem several times and look for key words and phrases. Identify the unknowns and assign variables. Next, translate the wording into a mathematical inequality. Finally, use the properties you have learned to solve the inequality and express the solution graphically or in interval notation.
Translate:
Five less than twice a number is at most \(25\).
Solution:
First, choose a variable for the unknown number and identify the key words and phrases.
\(\begin{array}{cccc}{\color{Cerulean}{twice\:a\:number}}&{\color{Cerulean}{five\:less\:than}}&{\color{Cerulean}{is\:at\:most}}&{}\\{\overbrace{\:\:2n\:\:}}&{\overbrace{\:\:-\:\:5\:\:}}&{\overbrace{\:\:\leq\:\:}}&{25} \end{array}\)
Answer:
\(2n−5≤25\).
The key phrase “is at most” indicates that the quantity has a maximum value of \(25\) or smaller.
The temperature in the desert can range from \(10°C\) to \(45°C\) in one \(24\)-hour period. Find the equivalent range in degrees Fahrenheit, \(F\), given that \(C=\frac{5}{9}(F−32)\).
Solution:
Set up a compound inequality where the temperature in Celsius is inclusively between \(10°C\) and \(45°C\). Then substitute the expression equivalent to the Celsius temperature in the inequality and solve for \(F\).
\(\begin{array}{c}{10°C\leq\color{OliveGreen}{temperature\:in\:Celsius}\color{black}{\leq 45°C}}\\{10\leq\color{OliveGreen}{\frac{5}{9}(F-32)}\color{black}{\leq 45}}\\{\color{Cerulean}{\frac{9}{5}\cdot}\color{black}{10\leq}\color{Cerulean}{\frac{9}{5}\cdot}\color{black}{\frac{5}{9}(F-32)\leq}\color{Cerulean}{\frac{9}{5}\cdot}\color{black}{45}}\\{18\leq F-32\leq 81}\\{18\color{Cerulean}{+32}\color{black}{\leq F-32}\color{Cerulean}{+32}\color{black}{\leq 81}\color{Cerulean}{+32}}\\{50\leq F\leq 113}\end{array}\)
Answer:
The equivalent Fahrenheit range is from \(50°F\) to \(113°F\).
In the first four events of a meet, a gymnast scores \(7.5, 8.2, 8.5\), and \(9.0\). What must she score on the fifth event to average at least \(8.5\)?
Solution:
The average must be at least \(8.5\); this means that the average must be greater than or equal to \(8.5\).
\(\begin{aligned} average &\geq 5 \\ \frac{7.5+8.2+8.5+9.0+x}{5}&\geq 8.5 \\ \frac{33.2+x}{5}&\geq 8.5 \\ \color{Cerulean}{5\cdot}\color{black}{\frac{33.2+x}{5}}&\geq\color{Cerulean}{5\cdot}\color{black}{8.5} & & \color{Cerulean}{Multiply\:both\:sides\:by\:5.} \\ 33.2+x&\geq 42.5 \\ 33.2+x\color{Cerulean}{-33.2}&\geq 42.5\color{Cerulean}{-33.2} \\ x&\geq 9.3 \end{aligned}\)
Answer:
She must score at least \(9.3\) on the fifth event.
Key Takeaways
- Inequalities typically have infinitely many solutions. The solutions are presented graphically on a number line or using interval notation or both.
- All but one of the rules for solving linear inequalities are the same as for solving linear equations. If you divide or multiply an inequality by a negative number, reverse the inequality to obtain an equivalent inequality.
- Compound inequalities involving the word “or” require us to solve each inequality and form the union of each solution set. These are the values that solve at least one of the given inequalities.
- Compound inequalities involving the word “and” require the intersection of the solution sets for each inequality. These are the values that solve both or all of the given inequalities.
- The general guidelines for solving word problems apply to applications involving inequalities. Be aware of a new list of key words and phrases that indicate a mathematical setup involving inequalities.
Determine whether the given number is a solution to the given inequality.
- \(2x−3<6; x=-1\)
- \(-3x+1\leq 0; x=-2\)
- \(5x-20>0; x=3\)
- \(\frac{1}{2}x+1>−\frac{3}{4}; x=−\frac{1}{4}\)
- \(−5<7x+1<9; x=0\)
- \(−20≤−3x−5≤−10; x=5\)
- \(x<-3 \text{ or }x>3; x=−10\)
- \(x<0\text{ or }x≥1; x=\frac{1}{2}\)
- \(2x+1<−3\text{ or }2x+1≥5; x=2\)
- \(4x−1<−17\text{ or }3x+2≥6; x=1\)
- Answer
-
1. Yes
3. No
5. Yes
7. Yes
9. Yes
Solve and graph the solution set. In addition, present the solution set in interval notation.
- \(x+5>1\)
- \(x−3<−4\)
- \(6x≤24\)
- \(4x>−8\)
- \(−7x≤14\)
- \(−2x+5>9\)
- \(7x−3≤25\)
- \(12x+7>−53\)
- \(−2x+5<-7\)
- \(-2x+4\leq 4\)
- \(-15x+10>20\)
- \(−8x+1≤29\)
- \(\frac{1}{7}x−3<1\)
- \(\frac{1}{2}x−\frac{1}{3}>\frac{2}{3}\)
- \(\frac{5}{3}x+\frac{1}{2}≤\frac{1}{3}\)
- \(−\frac{3}{4}x−\frac{1}{2}≥\frac{5}{2}\)
- \(−\frac{1}{5}x+\frac{3}{4}<−\frac{1}{5}\)
- \(−\frac{2}{3}x+1<-3\)
- \(2(-3x+1)<14\)
- \(-7(x-2)+1<15\)
- \(9x-3(3x+4)>−12\)
- \(12x−4(3x+5)≤−2\)
- \(5−3(2x−6)≥−1\)
- \(9x−(10x−12)<22\)
- \(2(x-7)-3(x+3)\leq -3\)
- \(5x-3>3x+7\)
- \(4(3x−2)≤−2(x+3)+12\)
- \(5(x−3)≥15x−(10x+4)\)
- \(12x+1>2(6x−3)−5\)
- \(3(x−2)+5>2(3x+5)+2\)
- \(−4(3x−1)+2x≤2(4x−1)−3\)
- \(−2(x−2)+14x<7(2x+1) \)
- Answer
-
1. \(x>−4; (−4, ∞)\)

Figure \(\PageIndex{8}\)
3. \(x≤4; (−∞, 4]\)
.png?revision=1)
Figure \(\PageIndex{9}\)
5. \(x≥−2; [−2, ∞)\)

Figure \(\PageIndex{10}\)
7. \(x≤4; (−∞, 4]\)
.png?revision=1)
Figure \(\PageIndex{11}\)
9. \(x>6; (6, ∞)\)
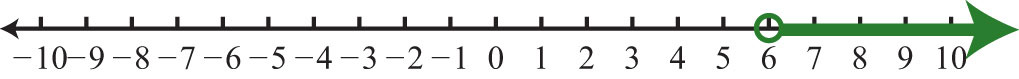
Figure \(\PageIndex{12}\)
11. \(x<−\frac{2}{3}; (−∞, −\frac{2}{3})\)
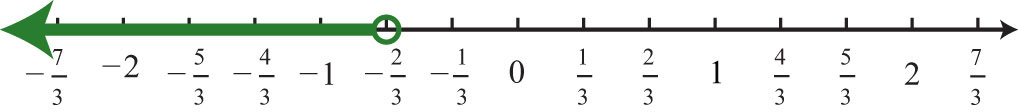
Figure \(\PageIndex{13}\)
13. \(x<28; (−∞, 28)\)
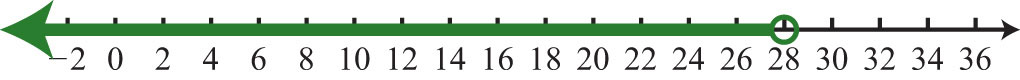
Figure \(\PageIndex{14}\)
15. \(x≤−\frac{1}{10}; (−∞, −\frac{1}{10}]\)

Figure \(\PageIndex{15}\)
17. \(x>\frac{19}{4}; (\frac{19}{4}, ∞)\)

Figure \(\PageIndex{16}\)
19. \(x>−2; (−2, ∞)\)
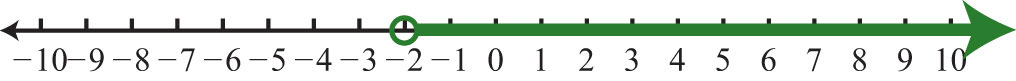
Figure \(\PageIndex{17}\)
21. \(∅\)
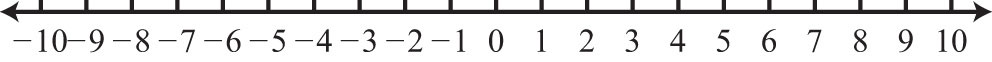
Figure \(\PageIndex{18}\)
23. \(x≤4; (−∞, 4]\)
.png?revision=1)
Figure \(\PageIndex{19}\)
25. \(x≥−20; [−20, ∞)\)

Figure \(\PageIndex{20}\)
27. \(x≤1; (−∞, 1]\)
.png?revision=1)
Figure \(\PageIndex{21}\)
29. \(R\)
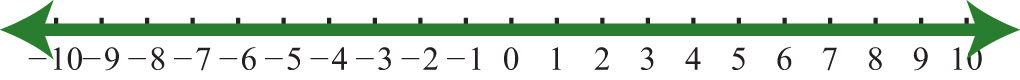
Figure \(\PageIndex{22}\)
31. \(x≥\frac{1}{2}; [\frac{1}{2}, ∞)\)

Figure \(\PageIndex{23}\)
Set up an algebraic inequality and then solve it.
- The sum of three times a number and \(4\) is greater than negative \(8\).
- The sum of \(7\) and three times a number is less than or equal to \(1\).
- When a number is subtracted from \(10\), the result is at most \(12\).
- When \(5\) times a number is subtracted from \(6\), the result is at least \(26\).
- If five is added to three times a number, then the result is less than twenty.
- If three is subtracted from two times a number, then the result is greater than or equal to nine.
- Bill earns $\(12.00\) for the day plus $\(0.25\) for every person he gets to register to vote. How many people must he register to earn at least $\(50.00\) for the day?
- With a golf club membership costing $\(100\) per month, each round of golf costs only $\(25.00\). How many rounds of golf can a member play if he wishes to keep his costs to $\(250\) per month at most?
- Joe earned scores of \(72, 85\), and \(75\) on his first three algebra exams. What must he score on the fourth exam to average at least \(80\)?
- Maurice earned \(4, 7\), and \(9\) points out of \(10\) on the first three quizzes. What must he score on the fourth quiz to average at least \(7\)?
- A computer is set to shut down if the temperature exceeds \(40°C\). Give an equivalent statement using degrees Fahrenheit. (Hint: \(C=\frac{5}{9}(F−32)\).)
- A certain brand of makeup is guaranteed not to run if the temperature is less than \(35°C\). Give an equivalent statement using degrees Fahrenheit.
- Answer
-
1. \(n>−4\)
3. \(n≥−2\)
5. \(n<5\)
7. Bill must register at least \(152\) people.
9. Joe must earn at least an \(88\) on the fourth exam.
11. The computer will shut down when the temperature exceeds \(104\)°F.
Solve and graph the solution set. In addition, present the solution set in interval notation.
- \(−1<x+3<5\)
- \(−10≤5x<20\)
- \(−2≤4x+6<10\)
- \(−10≤3x−1≤−4\)
- \(−15<3x−6≤6\)
- \(−22<5x+3≤3\)
- \(−1≤\frac{1}{2}x−5≤1\)
- \(1<8x+5<5\)
- \(−\frac{1}{5}≤\frac{2}{3}x−\frac{1}{5}<\frac{4}{5}\)
- \(−\frac{1}{2}<\frac{3}{4}x−\frac{2}{3}≤\frac{1}{2}\)
- \(−3≤3(x−1)≤3\)
- \(−12<6(x−3)≤0\)
- \(4<−2(x+3)<6\)
- \(−5≤5(−x+1)<15\)
- \(−\frac{3}{2}≤\frac{1}{4}(\frac{1}{2}x−1)+\frac{3}{4}<\frac{3}{2}\)
- \(−4≤−\frac{1}{3}(3x+12)<4\)
- \(−2≤12−2(x−3)≤20\)
- \(−5<2(x-1)-3(x+2)<5\)
- \(3x\leq -15\text{ or }2x>6\)
- \(4x−1<-17\text{ or }3x+2\geq 8\)
- \(-2x+1<-1\text{ or }-2x+1>1\)
- \(7x+4≤4\text{ or }6x−5≥1\)
- \(3x−7<14\text{ or }2x+3>7\)
- \(−3x+1<-5\text{ or }-4x-3>−23\)
- \(\frac{1}{2}x−2<-1\text{ or }\frac{1}{2}x-2>1\)
- \(\frac{1}{3}x+3≥−2\text{ or }\frac{1}{3}x+3≤2\)
- \(3x+7≤7\text{ or }−5x+6>6\)
- \(−10x−3≤17\text{ or }20x−6>−26\)
- \(2x−10<-2\text{ or }-3x+4>−5\)
- \(5x+3<4\text{ or }5-10x>4\)
- \(3x<18\text{ and }5x>-20\)
- \(x+7\leq 5\text{ and } x−3≥−10\)
- \(2x−1<5\text{ and }3x-1<10\)
- \(5x+2<-13\text{ and }3x+4>13\)
- Answer
-
1. \(−4<x<2; (-4,2)\)
.png?revision=1)
Figure \(\PageIndex{24}\)
3. \(−2≤x<1; [−2, 1)\)
.png?revision=1)
Figure \(\PageIndex{25}\)
5. \(-3<x\leq 4; (-3,4]\)
.png?revision=1)
Figure \(\PageIndex{26}\)
7. \(8≤x≤12; [8, 12]\)
.png?revision=1)
Figure \(\PageIndex{27}\)
9. \(0≤x<\frac{3}{2}; [0, \frac{3}{2})\)
.png?revision=1)
Figure \(\PageIndex{28}\)
11. \(0≤x≤2; [0, 2]\)
.png?revision=1)
Figure \(\PageIndex{29}\)
13. \(-6<x<-5; (-6,-5)\)
.png?revision=1)
Figure \(\PageIndex{30}\)
15. \(−16≤x<8; [−16, 8)\)
.png?revision=1)
Figure \(\PageIndex{31}\)
17. \(−1≤x≤10; [−1, 10]\)
.png?revision=1)
Figure \(\PageIndex{32}\)
19. \(x≤−5\text{ or }x>3; (−∞, −5]∪(3, ∞)\)
.png?revision=1)
Figure \(\PageIndex{33}\)
21. \(x>1\text{ or }x<0; (−∞, 0)∪(1, ∞)\)
.png?revision=1)
Figure \(\PageIndex{34}\)
23. \(R\)
.png?revision=1)
Figure \(\PageIndex{35}\)
25. \(x<2\text{ or }x>6; (−∞, 2)∪(6, ∞) \)
.png?revision=1)
Figure \(\PageIndex{36}\)
27. \(x≤0; (−∞, 0]\)
.png?revision=1)
Figure \(\PageIndex{37}\)
29. \(x<4; (−∞, 4)\)
.png?revision=1)
Figure \(\PageIndex{38}\)
31. \(-4<x<6; (-4,6)\)
.png?revision=1)
Figure \(\PageIndex{39}\)
33. \(x<3; (−∞, 3)\)
.png?revision=1)
Figure \(\PageIndex{40}\)
Set up a compound inequality for the following and then solve.
- Five more than two times some number is between \(15\) and \(25\).
- Four subtracted from three times some number is between \(−4\) and \(14\).
- Clint wishes to earn a B, which is at least \(80\) but less than \(90\). What range must he score on the fourth exam if the first three were \(65, 75\), and \(90\)?
- A certain antifreeze is effective for a temperature range of \(−35°C\) to \(120°C\). Find the equivalent range in degrees Fahrenheit.
- The average temperature in London ranges from \(23°C\) in the summer to \(14°C\) in the winter. Find the equivalent range in degrees Fahrenheit.
- If the base of a triangle measures \(5\) inches, then in what range must the height be for the area to be between \(10\) square inches and \(20\) square inches?
- A rectangle has a length of \(7\) inches. Find all possible widths if the area is to be at least \(14\) square inches and at most \(28\) square inches.
- A rectangle has a width of \(3\) centimeters. Find all possible lengths, if the perimeter must be at least \(12\) centimeters and at most \(26\) centimeters.
- The perimeter of a square must be between \(40\) feet and \(200\) feet. Find the length of all possible sides that satisfy this condition.
- If two times an angle is between \(180\) degrees and \(270\) degrees, then what are the bounds of the original angle?
- If three times an angle is between \(270\) degrees and \(360\) degrees then what are the bounds of the original angle?
- Answer
-
1. \(5<n<20\)
3. Clint must earn a score in the range from \(90\) to \(100\).
5. The average temperature in London ranges from \(57.2°F\) to \(73.4°F\).
7. The width must be at least \(2\) inches and at most \(4\) inches.
9. Sides must be between \(10\) feet and \(50\) feet.
11. The angle is between \(90\) degrees and \(120\) degrees.
- Research and discuss the use of set-builder notation with intersections and unions.
- Can we combine logical “or” into one statement like we do for logical “and”?
- Answer
-
2. Answers may vary


