6.2: Factoring Trinomials of the Form x²+bx+c
- Page ID
- 18363
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Factor trinomials of the form \(x^{2}+bx+c\).
- Factor trinomials using the AC method.
Factoring Trinomials of the Form \(x^{2}+bx+c\)
Some trinomials of the form \(x^{2}+bx+c\) can be factored as a product of binomials. For example,
\(x^{2}+7x+10=(x+2)(x+5)\)
We can verify this factorization by multiplying:
\(\begin{aligned}(x+2)(x+5)&=x^{2}+5x+2x+10\\&=x^{2}+7x+10\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Factoring trinomials requires that we work the distributive process in reverse. Notice that the product of the first terms of each binomial is equal to the first term of the trinomial.
\(x\cdot x=x^{2}\)
The middle term of the trinomial, \(7x\), is the sum of the products of the outer and inner terms of the binomials:
\(5x+2x=7x\)
And the product of the last terms of each binomial is equal to the last term of the trinomial.
\(2\cdot 5=10\)
This can be visually interpreted as follows:
.png?revision=1)
If a trinomial of this type factors, then these relationships will be true:
\(\begin{aligned} x^{2}+bx+c&=(x+m)(x+n) \\ &=x^{2}+nx+mx+mn \\ &=x^{2}+(n+m)x+mn \end{aligned}\)
This gives us
\[b=n+m \quad\text{and}\quad c=mn\]
In short, if the leading coefficient of a factorable trinomial is one, then the factors of the last term must add up to the coefficient of the middle term. This observation is the key to factoring trinomials using the technique known astrial and error (or guess and check). The steps are outlined in the following example.
Factor:
\(x^{2}+7x+12\)
Solution:
Note that the polynomial to be factored has three terms; it is a trinomial with a leading coefficient of \(1\). Use trial and error to factor as follows:
Step 1: Write two sets of blank parentheses. If a trinomial of this form factors, then it will factor into two linear binomial factors.
\(x^{2}+7x+12=(\quad )(\quad )\)
Step 2: Write the factors of the first term in the first space of each set of parentheses. In this case, factor \(x^{2}=x⋅x\).
\(x^{2}+7x+12=(x\quad )(x\quad )\)
Step 3: Determine the factors of the last term whose sum equals the coefficient of the middle term. To do this, list all of the factorizations of \(12\) and search for factors whose sum equals the coefficient of the middle term, \(7\).
\(\begin{aligned} 12&=1\cdot 12 & \rightarrow 1+12=13 \\ &=2\cdot 6 &\rightarrow 2+6=8 \\ &=\color{OliveGreen}{3\cdot 4} &\color{OliveGreen}{\rightarrow 3+4=7} \end{aligned}\)
Choose \(12 = 3 ⋅ 4\) because \(3 + 4 = 7\).
Step 4: Write in the last term of each binomial using the factors determined in the previous step.
\(x^{2}+7x+12=(x+3)(x+4)\)
Step 5: Check by multiplying the two binomials.
\(\begin{aligned} (x+3)(x+4)&=x^{2}+4x+3x+12 \\ &=x^{2}+7x+12\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Answer:
\((x+3)(x+4)\)
Since multiplication is commutative, the order of the factors does not matter.
\(\begin{aligned}x^{2}+7x+12&=(x+3)(x+4) \\ &=(x+4)(x+3) \end{aligned}\)
If the last term of the trinomial is positive, then either both of the constant factors must be negative or both must be positive. Therefore, when looking at the list of factorizations of the last term, we are searching for sums that are equal to the coefficient of the middle term.
Factor:
\(x^{2}-9x+20\).
Solution:
First, factor \(x^{2}=x⋅x\).
\(x^{2}-9x+20=(x\quad\color{Cerulean}{?}\color{black}{)(x}\quad\color{Cerulean}{?}\color{black}{)}\)
Next, determine which factors of \(20\) add up to \(−9\):
\(\begin{aligned}20&=1\cdot 20 \\&-2\cdot 10\\ &=4\cdot 5 \end{aligned}\)
In this case, choose \(−4\) and \(−5\) because \((−4)(−5)=+20\) and \(−4+(−5)=−9\).
\(x^{2}-9x+20=(x-4)(x-5)\)
Check.
\(\begin{aligned} (x-4)(x-5)&=x^{2}-5x-4x+20 \\ &=x^{2}-9x+20\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Answer:
\((x-4)(x-5)\)
If the last term of the trinomial is negative, then one of its factors must be negative. In this case, search the list of factorizations of the last term for differences that equal the coefficient of the middle term.
Factor:
\(x^{2}-4x-12\).
Solution:
Begin by factoring the first term \(x^{2}=x⋅x\).
\(x^{2}-4x-12=(x\quad\color{Cerulean}{?}\color{black}{)(x}\quad\color{Cerulean}{?}\color{black}{)}\)
The factors of \(12\) are listed below. In this example, we are looking for factors whose difference is \(−4\).
Here choose the factors \(2\) and \(−6\) because the coefficient of the middle term, \(−4\), is obtained if we add \(2+(−6)\).
\(x^{2}-4x-12=(x+2)(x-6)\)
Multiply to check.
Answer:
\((x+2)(x-6)\)
Often our first guess will not produce a correct factorization. This process may require repeated trials. For this reason, the check is very important and is not optional.
Factor:
\(x^{2}+5x-6\).
Solution:
The first term of this trinomial \(x^{2}\) factors as \(x⋅x\).
\(x^{2}+5x-6=(x\quad ?)(x\quad ?)
Consider the factors of \(6\):
\(\begin{aligned}6&=1\cdot 6 \\ &=2\cdot 3 \end{aligned}\)
Suppose we choose the factors \(2\) and \(3\) because \(2 + 3 = 5\), the coefficient of the middle term. Then we have the following incorrect factorization:
\(x^{2}+5x-6\color{black}{\stackrel{\color{red}{?}}{=}}(x+2)(x+3)\)
When we multiply to check, we find the error.
\(\begin{aligned}(x+2)(x+3)&=x^{2}+3x+2x+6 \\ &=x^{2}+5x\color{red}{+6\qquad x} \end{aligned}\)
In this case, the middle term is correct but the last term is not. Since the last term in the original expression is negative, we need to choose factors that are opposite in sign. Therefore, we must try again. This time we choose the factors \(−1\) and \(6\) because \(−1+6=5\).
\(x^{2}+5x-6=(x-1)(x+6)\)
Now the check shows that this factorization is correct.
Answer:
\((x-1)(x+6)\)
If we choose the factors wisely, then we can reduce much of the guesswork in this process. However, if a guess is not correct, do not get discouraged; just try a different set of factors.
Factor:
\(x^{2}+3x+20\).
Solution:
\(\begin{aligned} x^{2}+3x+20&=(x\quad\color{Cerulean}{?}\color{black}{)(x}\quad\color{Cerulean}{?}\color{black}{)} \\ 20&=1\cdot 20 \\ &=2\cdot 10 \\ &=4\cdot 5 \end{aligned}\)
Here there are no factors of \(20\) whose sum is \(3\). Therefore, the original trinomial cannot be factored as a product of two binomials. This trinomial is prime.
Answer:
Prime
Factor:
\(x^{2}-13x-30\).
- Answer
-
\((x+2)(x−15)\)
The techniques described can also be used to factor trinomials with more than one variable.
Factor:
\(x^{2}-14xy-72y^{2}\)
Solution:
The first term \(x^{2}\) factors as \(x⋅x\).
\(x^{2}+xy-72y^{2}=(x\quad\color{Cerulean}{?}\color{black}{)(x}\quad\color{Cerulean}{?}\color{black}{)}\)
Next, look for factors of the coefficient of the last term, \(72\), whose sum is \(−14\).
\(\begin{aligned} 72&=1\cdot 72 \\ &=2\cdot 36 \\ &=3\cdot 24 \\ &\color{OliveGreen}{=4\cdot 18} &\color{OliveGreen}{\rightarrow 4+(-18)=-14} \\ &=6\cdot 12 \\ &=8\cdot 9 \end{aligned}\)
Therefore, the coefficient of the last term can be factored \(−72=4(−18)\), where \(4+(−18)=−14\). Because the last term has a variable factor of \(y^{2}\), factor \(72y^{2}\) as \(4y(−18y)\) and try the following factorization:
\(x^{2}-14xy-72y^{2}=(x+4y)(x-18y)\)
Multiply to check.
\(\begin{aligned} (x+4y)(x-18y)&=x^{2}-18xy+4xy-72y^{2} \\ &=x^{2}-14xy-72y^{2}\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Visually, we have the following:
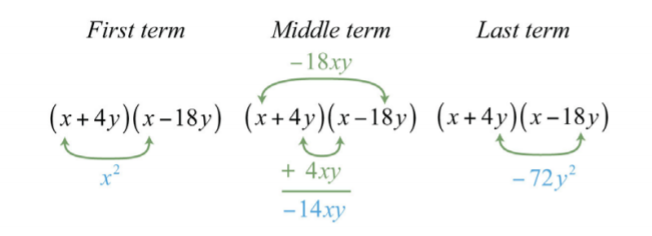.png?revision=1)
Answer:
\((x+4y)(x-18y)\)
Factor:
\(x^{2}y^{2}+9xy−10\).
- Answer
-
\((xy−1)(xy+10)\)
Factoring Using the AC Method
An alternate technique for factoring trinomials, called the AC method, makes use of the grouping method for factoring four-term polynomials. If a trinomial in the form \(ax^{2}+bx+c\) can be factored, then the middle term, \(bx\), can be replaced with two terms with coefficients whose sum is \(b\) and product \(ac\). This substitution results in an equivalent expression with four terms that can be factored by grouping. The steps are outlined in the following example.
Factor using the AC method:
\(x^{2}−x−30\).
Solution:
In this example \(a = 1, b = −1\), and \(c = −30\).
Step 1: Determine the product \(ac\).
Step 2: Find factors of \(ac\) whose sum equals the coefficient of the middle term, \(b\).
\(\begin{aligned} -30&=1(-30) \\ &=2(-15) \\ &=3(-10) \\ &=\color{OliveGreen}{5(-5)} &\color{OliveGreen}{\rightarrow\:5+(-6)=-1} \end{aligned}\)
We can see that the sum of the factors \(5\) and \(−6\) is equal to the coefficient of the middle term, \(−1\).
Step 3: Use the factors as coefficients for the terms that replace the middle term. Here \(−x=−6x+5x\). Write
\(x^{2}\color{OliveGreen}{-x}\color{black}{-30=x^{2}}\color{OliveGreen}{-6x+5x}\color{black}{-30}\)
Step 4: Factor the equivalent expression by grouping.
\(\begin{array}{cccc}{x^{2}-x-30=}&{\underbrace{x^{2}-6x}}&{+}&{\underbrace{5x-20}}\\{}&{\color{Cerulean}{group}}&{}&{\color{Cerulean}{group}} \end{array}\)
\(\begin{aligned} &=x(x-6)+5(x-6) \\ &=(x-6)(x+5) \end{aligned}\)
Answer:
\((x-6)(x+5)\)
Notice that the AC method is consistent with the trial and error method. Both methods require that \(b=m+n\), where \(c=mn\). In the example above, \(−30=(−6)(5)\) and \(−1=(−6)+5\). The only difference between the methods, when the leading coefficient is \(1\), is in the process used to obtain the final factorization.
Factor:
\(y^{2}-14x+48\).
Solution:
Here \(ac = 48\) and we search for factors whose sum is \(−14\).
\(\begin{aligned} 48&=1(48) \\ &=2(24)\\ &=3(16)\\ &=4(12)\\&=\color{OliveGreen}{6(8)} &\color{OliveGreen}{\rightarrow -6+(-8)=-14} \end{aligned}\)
Therefore, \(−14x=−6x−8x\). Substitute the new terms and factor by grouping.
\(\begin{aligned} y^{2}-14x+48&=x^{2}\color{OliveGreen}{-6x-8x}\color{black}{+48} \\ &=x(x-6)-8(x-6)\\&=(x-6)(x-8) \end{aligned}\)
Answer:
\((x-6)(x-8)\). The check is left to the reader.
At this point, it is recommended that the reader stop and factor as many trinomials of the form \(x^{2}+bx+c\) as time allows before moving on to the next section. Factoring trinomials is one of the more important skills that we learn in this course and should be mastered.
Key Takeaways
- Factor a trinomial by systematically guessing what factors give two binomials whose product is the original trinomial.
- If a trinomial of the form \(x^{2}+bx+c\) factors into the product of two binomials, then the coefficient of the middle term is the sum of factors of the last term.
- Not all trinomials can be factored as the product of binomials with integer coefficients. In this case, we call it a prime trinomial.
- Factoring is one of the more important skills required in algebra. For this reason, you should practice working as many problems as it takes to become proficient.
Are the following factored correctly? Check by multiplying.
- \(x^{2}+5x−6=(x+2)(x+3) \)
- \(x^{2}+6x+16=(x+8)(x−2) \)
- \(y^{2}+2y−8=(y+4)(y−2)\)
- \(y^{2}−10y+21=(y−3)(y−7) \)
- \(a^{2}−10a+25=(a−5)^{2}\)
- \(a^{2}+6a+9=(a−3)^{2}\)
- \(x^{2}+10x−25=(x+5)(x−5) \)
- \(x^{2}+5x+14=(x−2)(x+7) \)
- \(y^{2}+50y−600=(y+60)(y−10) \)
- \(y^{2}−3y+2=(y−2)(y−1)\)
- Answer
-
1. No
3. Yes
5. Yes
7. No
9. Yes
Factor.
- \(x^{2}+6x+8 \)
- \(x^{2}+4x+3 \)
- \(x^{2}+3x+2 \)
- \(x^{2}+x−2 \)
- \(x^{2} + 3 x −10 \)
- \(x^{ 2} − 2x −35 \)
- \(x^{ 2} −13 x +12 \)
- \(x^{ 2} −15 x +36 \)
- \(x^{ 2} −12x +36 \)
- \(x^{ 2} +18 x +81 \)
- \(x^{ 2} − 2x + 1 \)
- \(x^{ 2} −18 x +81 \)
- \(x^{ 2} + 5 x + 5 \)
- \(x^{ 2} − 4x + 6 \)
- \(x^{ 2} −20x +91 \)
- \(x^{ 2} +20x +91 \)
- \(x^{ 2} − 2x −48 \)
- \(x^{ 2} +16x +48 \)
- \(x^{ 2} +22x +48 \)
- \(x^{ 2} +22x −48 \)
- \(y^{ 2} + 7y +12 \)
- \(y^{ 2} + 8y −20 \)
- \(y^{ 2} −16y +60 \)
- \(y^{ 2} −31 y −32 \)
- \(a^{ 2} −11 a −42 \)
- \(a^{ 2} −14 a −51 \)
- \(a^{ 2} +26 a +25 \)
- \(a^{ 2} −22 a +120 \)
- \(a^{ 2} + 4 a − 1 \)
- \(a^{ 2} − 6 a + 2 \)
- \(y^{ 2} −14x +40 \)
- \(y^{ 2} − 4y −96\)
- \(x^{ 2} − 2xy +y^{ 2}\)
- \(x^{2}+2xy+y^{2}\)
- \(x^{2}−16xy+15y^{2}\)
- \(x^{2}−4xy−32y^{2}\)
- \(x^{2}+2xy−15y^{2}\)
- \(x^{2}−12xy+32y^{2}\)
- \(x^{2}y^{2}−6xy+9\)
- \(x^{2}y^{2}+25xy−26\)
- \(a^{2}+4ab+4b^{2}\)
- \(a^{2}−19ab−20b^{2}\)
- \(a^{2}−ab−12b^{2}\)
- \(a^{2}−10ab−56b^{2}\)
- \(a^{2}b^{2}−2ab−15\)
- \(a^{2}b^{2}−10ab+24\)
- The area of a square is given by the function \(A(x)=x^{2}−14x+49\), where \(x\) is measured in meters. Rewrite this function in factored form.
- The area of a square is given by the function \(A(x)=x^{2}+16x+64\), where \(x\) is measured in meters. Rewrite this function in factored form.
- Answer
-
1. \((x+2)(x+4)\)
3. \((x+1)(x+2)\)
5. \((x−2)(x+5)\)
7. \((x−1)(x−12)\)
9. \((x−6)^{2}\)
11. \((x−1)^{2}\)
13. Prime
15. \((x−7)(x−13)\)
17. \((x+6)(x−8) \)
19. Prime
21. \((y+3)(y+4)\)
23. \((y−6)(y−10)\)
25. \((a+3)(a−14)\)
27. \((a+1)(a+25)\)
29. Prime
31. \((y−10)(y−4)\)
33. \((x−y)^{2}\)
35. \((x−15y)(x−y)\)
37. \((x+5y)(x−3y)\)
39. \((xy−3)^{2}\)
41. \((a+2b)^{2}\)
43. \((a+3b)(a−4b)\)
45. \((ab+3)(ab−5)\)
45. \(A(x)=(x−7)^{2}\)
Factor using the AC method.
- \(x^{2}+5x−14 \)
- \(x^{2}+2x−48 \)
- \(x^{2}−9x+8 \)
- \(x^{2}−14x+24 \)
- \(x^{2}−x−72 \)
- \(x^{2}−x−90 \)
- \(y^{2}−8y+16 \)
- \(y^{2}+16y+64\)
- \(x^{2}+4x+12 \)
- \(x^{2}+5x−8\)
- \(x^{2}+3xy−18y2 \)
- \(x^{2}−15xy+50y^{2}\)
- Answer
-
1. \((x+7)(x−2)\)
3. \((x−8)(x−1)\)
5. \((x−9)(x+8)\)
7. \((y−4)^{2}\)
9. Prime
11. \((x+6y)(x−3y)\)
- Create your own trinomial of the form \(x^{2}+bx+c\) that factors. Share it along with the solution on the discussion board.
- Write out your own list of steps for factoring a trinomial of the form \(x^{2}+bx+c\) and share your steps on the discussion board.
- Create a trinomial that does not factor and share it along with an explanation of why it does not factor.
- Answer
-
1. Answers may vary
3. Answers may vary


