9.4: Guidelines for Solving Quadratic Equations and Applications
- Page ID
- 18385
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use the discriminant to determine the number and type of solutions to any quadratic equation.
- Develop a general strategy for solving quadratic equations.
- Solve applications involving quadratic equations.
Discriminant
If given a quadratic equation in standard form, \(ax^{2}+bx+c=0\), where a, b, and c are real numbers and a≠0, then the solutions can be calculated using the quadratic formula:
The solutions are rational, irrational, or not real. We can determine the type and number of solutions by studying the discriminant, the expression inside the radical, \(b^{2}−4ac\). If the value of this expression is negative, then the equation has no real solutions. If the discriminant is positive, then we have two real solutions. And if the discriminant is 0, then we have one real solution.
Example \(\PageIndex{1}\)
Determine the type and number of solutions:
\(x^{2}−10x+30=0\).
Solution:
We begin by identifying a, b, and c. Here
Substitute these values into the discriminant and simplify.
Since the discriminant is negative, we conclude that there are no real solutions.
Answer:
No real solution
If we use the quadratic formula in the previous example, we find that a negative radicand stops the process of simplification and shows that there is no real solution.
Note
We will study quadratic equations with no real solutions as we progress in our study of algebra.
Determine the type and number of solutions:
\(7x^{2}-10x+1=0\)
Solution:
Here
Substitute these values into the discriminant:
Since the discriminant is positive, we can conclude that there are two real solutions.
Answer:
Two real solutions
If we use the quadratic formula in the previous example, we find that a positive radicand in the quadratic formula leads to two real solutions.
The two real solutions are \(\frac{5-3 \sqrt{2}}{7}\) and \(\frac{5+3 \sqrt{2}}{7}\). Note that these solutions are irrational; we can approximate the values on a calculator.
Determine the type and number of solutions:
\(2x^{2}-7x-4=0\)
Solution:
In this example,
Substitute these values into the discriminant and simplify.
Since the discriminant is positive, we conclude that there are two real solutions. Furthermore, since the discriminant is a perfect square, we obtain two rational solutions.
Answer:
Two real solutions
We could solve the previous quadratic equation using the quadratic formula as follows:
\(\begin{array}{lll}{x=\frac{7-9}{4}} & {\text { or }} &{ x=\frac{7+9}{4}} \\ {x=\frac{-2}{4}} && {x=\frac{16}{4}} \\ {x=-\frac{1}{2}} && {x=4}\end{array}\)
If the discriminant is a perfect square, then we could have factored the original equation.
\(\begin{array}{rlr}{2 x+1} & {=0} & {\text { or }} & {x-4=0} \\ {2 x} & {=-1} & {} & {x=4} \\ {x} & {=-\frac{1}{2}}\end{array}\)
Given the special condition where the discriminant is 0, we obtain only one solution, a double root.
Determine the type and number of solutions:
\(9x^{2}-6x+1=0\)
Solution:
Here a=9, b=−6, and c=1, and we have
Since the discriminant is 0, we conclude that there is only one real solution, a double root.
Answer:
One real solution
Since 0 is a perfect square, we can solve the equation above by factoring.
\(\begin{array}{rrr}{3 x-1=0} & {\text { or } \quad 3 x-1=0} \\ {3 x=1} & {3 x=1} \\ {x=\frac{1}{3}} & {x=\frac{1}{3}}\end{array}\)
Here 1/3 is a solution that occurs twice; it is a double root.
In summary, if given any quadratic equation in standard form, \(ax^{2}+bx+c=0\), where a, b, and c are real numbers and a≠0, then we have the following:
| Positive discriminant: | \(b^{2}-4ac >0\) | Two real solutions |
|---|---|---|
| Zero discriminant: | \(b^{2}-4ac =0\) | One real solution |
| Negative discriminant: | \(b^{2}-4ac <0\) | No real solution |
As we will see, knowing the number and type of solutions ahead of time helps us determine which method is best for solving a quadratic equation.
Determine the number and type of solutions:
\(3x^{2}-5x+4=0\)
- Answer
-
No real solution
General Guidelines for Solving Quadratic Equations
Use the coefficients of a quadratic equation to help decide which method is most appropriate for solving it. While the quadratic formula always works, it is sometimes not the most efficient method. Given any quadratic equation in standard form, \(ax^{2}+bx+c=0\), general guidelines for determining the method for solving it follow:
- If c = 0, then factor out the GCF and solve by factoring.
- If b = 0, then solve by extracting the roots.
- If a, b, and c are all nonzero, then determine the value for the discriminant, \(b^{2}−4ac\):
- If the discriminant is a perfect square, then solve by factoring.
- If the discriminant is not a perfect square, then solve using the quadratic formula.
- If the discriminant is positive, we obtain two real solutions.
- If the discriminant is negative, then there is no real solution.
Solve:
\(15x^{2}-5x=0\)
Solution:
In this case, c = 0 and we can solve by factoring out the GCF.
\(\begin{array}{rlr}{5 x=0} & {\text { or } }&{ 3 x-1=0} \\ {x=0} && {3 x=1} \\ && {x=\frac{1}{3}}\end{array}\)
Answer:
The solutions are 0 and \(\frac{1}{3}\).
Solve:
\(3x^{2}-5=0\)
Solution:
In this case, b = 0 and we can solve by extracting the roots.
Answer:
The solutions are \(\pm \frac{\sqrt{15}}{3}\)
Example \(\PageIndex{7}\)
Solve:
\(9x^{2}-6x-7=0\)
Solution:
Begin by identifying a, b, and c as the coefficients of each term. Here
Substitute these values into the discriminant and then simplify.
Since the discriminant is positive and not a perfect square, use the quadratic formula and expect two real solutions.
Answer:
The solutions are \(=\frac{1 \pm 2 \sqrt{2}}{3}\)
Example \(\PageIndex{8}\)
Solve:
\(4 x(x-2)=-7\)
Solution:
Begin by rewriting the quadratic equation in standard form.
Here
Substitute these values into the discriminant and then simplify.
Since the discriminant is negative, the solutions are not real numbers.
Answer:
No real solution
Example \(\PageIndex{9}\)
Solve:
\((3x+5)(3x+7)=6x+10\)
Solution:
Begin by rewriting the quadratic equation in standard form.
\(\begin{aligned}(3 x+5)(3 x+7) &=6 x+10 \\ 9 x^{2}+21 x+15 x+35 &=6 x+10 \\ 9 x^{2}+36 x+35 &=6 x+10 \\ 9 x^{2}+30 x+25 &=0 \end{aligned}\)
Substitute a=9, b=30, and c=25 into the discriminant.
Since the discriminant is 0, solve by factoring and expect one real solution, a double root.
\(\begin{aligned} 9 x^{2}+30 x+25 &=0 \\(3 x+5)(3 x+5) &=0 \end{aligned}\)
\(\begin{array}{rrr}{3 x+5=0} & {\text { or } \quad 3 x+5=0} \\ {3 x=-5} & {3 x=-5} \\ {x=-\frac{5}{3}} & {x=-\frac{5}{3}}\end{array}\)
Answer:
The solution is \(-\frac{5}{3}\)
Solve:
\(5x^{2}+2x-7=2x-3\)
- Answer
-
\(\pm\frac{2 \sqrt{5}}{5}\)
Applications Involving Quadratic Equations
In this section, the algebraic setups usually consist of a quadratic equation where the solutions may not be integers.
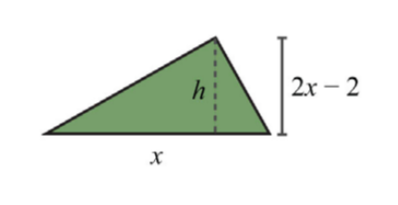
The height of a triangle is 2 inches less than twice the length of its base. If the total area of the triangle is 11 square inches, then find the lengths of the base and height. Round answers to the nearest hundredth
Solution:
.png?revision=1)
.png?revision=1)
Use the formula \(A=\frac{1}{2}bh\) and the fact that the area is 11 square inches to set up an algebraic equation.
\(\begin{array}{l}{A=\frac{1}{2} b \cdot h} \\ {\color{OliveGreen}{11}\color{black}{=}\frac{1}{2} x(\color{OliveGreen}{2 x-2}\color{black}{)}}\end{array}\)
To rewrite this quadratic equation in standard form, first distribute \(\frac{1}{2}x\).
\(\begin{array}{l}{11=\frac{1}{2} x(2 x-2)} \\ {11=x^{2}-x} \\ {0=x^{2}-x-11}\end{array}\)
Use the coefficients, a = 1, b = −1, and c = −11, to determine the type of solutions.
Since the discriminant is positive, expect two real solutions.
In this problem, disregard the negative solution and consider only the positive solution.
\(x=\frac{1+3 \sqrt{5}}{2}\)
Back substitute to find the height.
Answer:
The base measures \(\frac{-1+3 \sqrt{5}}{2}\approx 3.85\) inches and the height is \(-1+3 \sqrt{5} \approx 5.71\) inches.
Example \(\PageIndex{11}\)
The sum of the squares of two consecutive positive integers is 481. Find the integers.
Solution:
Let n represent the first positive integer.
Let n+1 represent the next positive integer.
The algebraic setup follows:
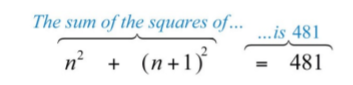.png?revision=1)
Rewrite the quadratic equation in standard form.
When the coefficients are large, sometimes it is less work to use the quadratic formula instead of trying to factor it. In this case, a=1, b=1, and c=−240. Substitute into the quadratic formula and then simplify.
\(\begin{array}{ll}{n=\frac{-1-31}{2}} & {n=\frac{-1+31}{2}} \\ {n=\frac{-32}{2}} & {n=\frac{30}{2}} \\ {n=-16} & {n=15}\end{array}\)
Since the problem calls for positive integers, disregard the negative solution and choose n = 15.
\(\begin{aligned} n+1 &=\color{OliveGreen}{15}\color{black}{+}1 \\ &=16 \end{aligned}\)
Answer:
The positive integers are 15 and 16.
Key Takeaways
- Determine the number and type of solutions to any quadratic equation in standard form using the discriminant, \(b^{2}−4ac\). If the discriminant is negative, then the solutions are not real. If the discriminant is positive, then the solutions are real. If the discriminant is 0, then there is only one solution, a double root.
- Choose the appropriate method for solving a quadratic equation based on the value of its discriminant. While the quadratic formula will solve any quadratic equation, it may not be the most efficient method.
- When solving applications, use the key words and phrases to set up an algebraic equation that models the problem. In this section, the setup typically involves a quadratic equation.
Calculate the discriminant and use it to determine the number and type of solutions. Do not solve.
- \(x^{2}+2x+3=0\)
- \(x^{2}−2x−3=0\)
- \(3x^{2}−1x−2=0\)
- \(3x^{2}−1x+2=0\)
- \(9y^{2}+2=0\)
- \(9y^{2}−2=0\)
- \(5x^{2}+x=0\)
- \(5x^{2}−x=0\)
- \(12x^{2}−2x+52=0\)
- \(12x^{2}−x−12=0\)
- \(−x^{2}−2x+4=0\)
- \(−x^{2}−4x+2=0\)
- \(4t^{2}−20t+25=0\)
- \(9t^{2}−6t+1=0\)
- Answer
-
1. −8, no real solution
3. 25, two real solutions
5. −72, no real solution
7. 1, two real solutions
9. −1, no real solution
11. 20, two real solutions
13. 0, one real solution
Choose the appropriate method to solve the following.
- \(x^{2}−2x−3=0\)
- \(x^{2}+2x+3=0\)
- \(3x^{2}−x−2=0\)
- \(3x^{2}−x+2=0\)
- \(9y^{2}+2=0\)
- \(9y^{2}−2=0\)
- \(5x^{2}+x=0\)
- \(5x^{2}−x=0\)
- \(12x^{2}−2x+52=0\)
- \(12x^{2}−x−12=0\)
- \(−x^{2}−2x+4=0\)
- \(−x^{2}−4x+2=0\)
- \(4t^{2}−20t+25=0\)
- \(9t^{2}−6t+1=0\)
- \(y^{2}−4y−1=0\)
- \(y^{2}−6y−3=0\)
- \(25x^{2}+1=0\)
- \(36x^{2}+4=0\)
- \(5t^{2}−4=0\)
- \(2t^{2}−9=0\)
- \(12x^{2}−94x+1=0\)
- \(3x^{2}+12x−16=0\)
- \(36y^{2}=2y\)
- \(50y^{2}=−10y\)
- \(x(x−6)=−29\)
- \(x(x−4)=−16\)
- \(4y(y+1)=5\)
- \(2y(y+2)=3\)
- \(-3x^{2}=2x+1\)
- \(3x^{2}+4x=−2\)
- \(6(x+1)2=11x+7\)
- \(2(x+2)2=7x+11\)
- \(9t^{2}=4(3t−1)\)
- \(5t(5t−6)=−9\)
- \((x+1)(x+7)=3\)
- \((x−5)(x+7)=14\)
- Answer
-
1. \(-1, 3\)
3. \(-\frac{2}{3} , 1\)
5. No real solution
7. \(-\frac{1}{5} , 0\)
9. No real solution
11. \(-1\pm\sqrt{5}\)
13. \(\frac{5}{2}\)
15. \(2\pm\sqrt{5}\)
17. No real solution
19. \(\pm\frac{2 \sqrt{5}}{5}\)
21. \(\frac{1}{2}, 4\)
23. \(0, \frac{1}{18}\)
25. No real solution
27. \(\frac{-1\pm\sqrt{6}}{2}\)
29. No real solution
31. \(-\frac{1}{2}, \frac{1}{3}\)
33.\(\frac{2}{3}\)
35. \(-4\pm 2\sqrt{3}\)
Set up an algebraic equation and use it to solve the following.
- A positive real number is 2 less than another. When 4 times the larger is added to the square of the smaller, the result is 49. Find the numbers.
- A positive real number is 1 more than another. When twice the smaller is subtracted from the square of the larger, the result is 4. Find the numbers.
- A positive real number is 6 less than another. If the sum of the squares of the two numbers is 38, then find the numbers.
- A positive real number is 1 more than twice another. If 4 times the smaller number is subtracted from the square of the larger, then the result is 21. Find the numbers.
- Answer
-
1. \(3\sqrt{5}\) and \(3\sqrt{5}-2)
3. \(\sqrt{10\pm 3\)
Round off your answers to the nearest hundredth.
- The area of a rectangle is 60 square inches. If the length is 3 times the width, then find the dimensions of the rectangle.
- The area of a rectangle is 6 square feet. If the length is 2 feet more than the width, then find the dimensions of the rectangle.
- The area of a rectangle is 27 square meters. If the length is 6 meters less than 3 times the width, then find the dimensions of the rectangle.
- The area of a triangle is 48 square inches. If the base is 2 times the height, then find the length of the base.
- The area of a triangle is 14 square feet. If the base is 4 feet more than 2 times the height, then find the length of the base and the height.
- The area of a triangle is 8 square meters. If the base is 4 meters less than the height, then find the length of the base and the height.
- The perimeter of a rectangle is 54 centimeters and the area is 180 square centimeters. Find the dimensions of the rectangle.
- The perimeter of a rectangle is 50 inches and the area is 126 square inches. Find the dimensions of the rectangle.
- George maintains a successful 6-meter-by-8-meter garden. Next season he plans on doubling the planting area by increasing the width and height by an equal amount. By how much must he increase the length and width?
- A uniform brick border is to be constructed around a 6-foot-by-8-foot garden. If the total area of the garden, including the border, is to be 100 square feet, then find the width of the brick border.
- Answer
-
1. Length: 13.42 inches; width: 4.47 inches
3. Length: 6.48 meters; width: 4.16 meters
5. Height: 2.87 feet; base: 9.74 feet
7. Length: 15 centimeters; width: 12 centimeters
9. 2.85 meters
- If the sides of a square measure \(\sqrt{106}\) units, then find the length of the diagonal.
- If the diagonal of a square measures \(\sqrt{310}\) units, then find the length of each side.
- The diagonal of a rectangle measures \(\sqrt{63}\) inches. If the width is 4 inches less than the length, then find the dimensions of the rectangle.
- The diagonal of a rectangle measures \(\sqrt{23}\) inches. If the width is 2 inches less than the length, then find the dimensions of the rectangle.
- The top of a 20-foot ladder, leaning against a building, reaches a height of 18 feet. How far is the base of the ladder from the wall? Round off to the nearest hundredth.
- To safely use a ladder, the base should be placed about 1/4 of the ladder’s length away from the wall. If a 20-foot ladder is to be safely used, then how high against a building will the top of the ladder reach? Round off to the nearest hundredth.
- The diagonal of a television monitor measures 32 inches. If the monitor has a 3:2 aspect ratio, then determine its length and width. Round off to the nearest hundredth.
- The diagonal of a television monitor measures 52 inches. If the monitor has a 16:9 aspect ratio, then determine its length and width. Round off to the nearest hundredth.
- Answer
-
1. \(\sqrt{203}\) units
3. Length: \(2+\sqrt{52}\) inches; width: \(−2+\sqrt{52}\) inches
5. \(2\sqrt{19} \approx 8.72\) feet
7. Length: 26.63 inches; width: 17.75 inches
- The profit in dollars of running an assembly line that produces custom uniforms each day is given by the function \(P(t)=−40t^{2}+960t−4,000\), where t represents the number of hours the line is in operation.
- Calculate the profit on running the assembly line for 10 hours a day.
- Calculate the number of hours the assembly line should run in order to break even. Round off to the nearest tenth of an hour.
- The profit in dollars generated by producing and selling x custom lamps is given by the function \(P(x)=−10x^{2}+800x−12,000\).
- Calculate the profit on the production and sale of 35 lamps.
- Calculate the number of lamps that must be sold to profit $3,000.
- If $1,200 is invested in an account earning an annual interest rate r, then the amount A that is in the account at the end of 2 years is given by the formula \(A=1,200(1+r)^{2}\). If at the end of 2 years the amount in the account is $1,335.63, then what was the interest rate?
- A manufacturing company has determined that the daily revenue, R, in thousands of dollars depends on the number, n, of palettes of product sold according to the formula \(R=12n−0.6n^{2}\). Determine the number of palettes that must be sold in order to maintain revenues at $60,000 per day.
- Answer
-
1. a. $1,600; b. 5.4 hours and 18.6 hours
3. 5.5%
- The height of a projectile launched upward at a speed of 32 feet/second from a height of 128 feet is given by the function \(h(t)=−16t^{2}+32t+128\).
- What is the height of the projectile at 1/2 second?
- At what time after launch will the projectile reach a height of 128 feet?
- The height of a projectile launched upward at a speed of 16 feet/second from a height of 192 feet is given by the function \(h(t)=−16t^{2}+16t+192\).
- What is the height of the projectile at 3/2 seconds?
- At what time will the projectile reach 128 feet?
- The height of an object dropped from the top of a 144-foot building is given by \(h(t)=−16t^{2}+144\). How long will it take to reach a point halfway to the ground?
- The height of a projectile shot straight up into the air at 80 feet/second from the ground is given by \(h(t)=−16t^{2}+80t\). At what time will the projectile reach 95 feet?
- Answer
-
1. a. 140 feet; b. 0 seconds and 2 seconds
3. 2.12 seconds
- Discuss the strategy of always using the quadratic formula to solve quadratic equations.
- List all of the methods that we have learned so far to solve quadratic equations. Discuss the pros and cons of each.
- Answer
-
1. Answers may vary


