1.11: Systems of Measurement
- Page ID
- 15126
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Make unit conversions in the US system
- Use mixed units of measurement in the US system
- Make unit conversions in the metric system
- Use mixed units of measurement in the metric system
- Convert between the US and the metric systems of measurement
- Convert between Fahrenheit and Celsius temperatures
A more thorough introduction to the topics covered in this section can be found in the Prealgebra chapter, The Properties of Real Numbers.
Make Unit Conversions in the U.S. System
There are two systems of measurement commonly used around the world. Most countries use the metric system. The U.S. uses a different system of measurement, usually called the U.S. system. We will look at the U.S. system first.
The U.S. system of measurement uses units of inch, foot, yard, and mile to measure length and pound and ton to measure weight. For capacity, the units used are cup, pint, quart, and gallons. Both the U.S. system and the metric system measure time in seconds, minutes, and hours.
The equivalencies of measurements are shown in Table \(\PageIndex{1}\). The table also shows, in parentheses, the common abbreviations for each measurement.
| U.S. System of Measurement | |
|---|---|
| \(\begin{array} {llll} {} &{\text{1 foot (ft.)}} &{=} &{\text{12 inches (in.)}} \\ {\textbf{Length}} &{\text{1 yard (yd.)}} &{=} &{\text{3 feet (ft.)}} \\ {} &{\text{1 mile (mi.)}} &{=} &{\text{5280 feet (ft.)}} \end{array}\) | \(\begin{array} {llll} {} &{\text{3 teaspoons (t)}} &{=} &{\text{1 tablespoon (T)}} \\ {} &{\text{16 tablespoons (T)}} &{=} &{\text{1 cup (C)}} \\ {} &{\text{1 cup (C)}} &{=} &{\text{8 fluid ounces (fl.oz.)}} \\ {\textbf{Volume}} &{\text{1 pint (pt.)}} &{=} &{\text{2 cups (C)}} \\ {} &{\text{1 quart (qt.)}} &{=} &{\text{2 pints (ft.)}} \\ {} &{\text{1 gallon (gal)}} &{=} &{\text{4 quarts (qt.)}} \end{array}\) |
|
\(\begin{array} {llll} {\textbf{Weight}} &{\text{1 pound (lb.)}} &{=} &{\text{16 ounces (oz.)}} \\ {} &{\text{1 ton}} &{=} &{\text{2000 pounds (lb.)}} \end{array}\) |
\(\begin{array} {llll} {} &{\text{1 minute (min)}} &{=} &{\text{60 seconds (sec)}} \\ {} &{\text{1 hour (hr)}} &{=} &{\text{60 minutes (min)}} \\ {\textbf{Time}} &{\text{1 day}} &{=} &{\text{24 hours (hr)}} \\ {} &{\text{1 week (wk)}} &{=} &{\text{7 days}} \\ {} &{\text{1 year (yr)}} &{=} &{\text{365 days}} \end{array}\) |
In many real-life applications, we need to convert between units of measurement, such as feet and yards, minutes and seconds, quarts and gallons, etc. We will use the identity property of multiplication to do these conversions. We’ll restate the identity property of multiplication here for easy reference.
\(\begin{array} { l l } { \text {For any real number } a : } & { a \cdot 1 = a \quad 1 \cdot a = a } \\ { \textbf{1} \text { is the } \textbf{multiplicative identity } } \end{array}\)
To use the identity property of multiplication, we write 1 in a form that will help us convert the units. For example, suppose we want to change inches to feet. We know that 1 foot is equal to 12 inches, so we will write 1 as the fraction \(\frac{\text{1 foot}}{\text{12 inches}}\). When we multiply by this fraction we do not change the value, but just change the units.
But \(\frac{\text{12 inches}}{\text{1 foot}}\) also equals 1. How do we decide whether to multiply by \(\frac{\text{1 foot}}{\text{12 inches}}\) or \(\frac{\text{12 inches}}{\text{1 foot}}\)? We choose the fraction that will make the units we want to convert from divide out. Treat the unit words like factors and “divide out” common units like we do common factors. If we want to convert 6666 inches to feet, which multiplication will eliminate the inches?

The inches divide out and leave only feet. The second form does not have any units that will divide out and so will not help us.
Mary Anne is 66 inches tall. Convert her height into feet.
Solution




Lexie is 30 inches tall. Convert her height to feet.
- Answer
-
2.5 feet
Rene bought a hose that is 18 yards long. Convert the length to feet.
- Answer
-
54 feet
- Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
- Multiply.
- Simplify the fraction.
- Simplify.
When we use the identity property of multiplication to convert units, we need to make sure the units we want to change from will divide out. Usually this means we want the conversion fraction to have those units in the denominator.
Ndula, an elephant at the San Diego Safari Park, weighs almost 3.2 tons. Convert her weight to pounds.
Solution
We will convert 3.2 tons into pounds. We will use the identity property of multiplication, writing 1 as the fraction \(\frac{\text{2000 pounds}}{\text{1 ton}}\).
| \(\text{3.2 tons}\) | |
| Multiply the measurement to be converted, by 1. | \(\text{3.2 tons} \cdot 1\) |
| Write 1 as a fraction relating tons and pounds. | \(\text{3.2 tons} \cdot \frac{\text{2000 pounds}}{\text{1 ton}}\) |
| Simplify. | 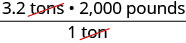 |
| Multiply. | 6400 pounds |
| Ndula weighs almost 6400 pounds. |
Arnold’s SUV weighs about 4.3 tons. Convert the weight to pounds.
- Answer
-
8600 pounds
The Carnival Destiny cruise ship weighs 51000 tons. Convert the weight to pounds.
- Answer
-
102000000 pounds
Sometimes, to convert from one unit to another, we may need to use several other units in between, so we will need to multiply several fractions.
Juliet is going with her family to their summer home. She will be away from her boyfriend for 9 weeks. Convert the time to minutes.
Solution
To convert weeks into minutes we will convert weeks into days, days into hours, and then hours into minutes. To do this we will multiply by conversion factors of 1.
| 9 weeks | |
| Write 1 as \(\frac{\text{7 days}}{\text{1 week}}\), and \(\frac{\text{60 minutes}}{\text{1 hour}}\). | \(\frac{\text{9 wk}}{\text{1}}\cdot\frac{\text{7 days}}{\text{1 wk}}\cdot\frac{\text{24 hr}}{\text{1 day}}\cdot\frac{\text{60 min}}{\text{1 hr}}\) |
| Divide out the common units. |  |
| Multiply. | \(\frac{9\cdot7\cdot24\cdot60\text{ min}}{1\cdot1\cdot1\cdot1}\) |
| Multiply. | 90,720 min |
Juliet and her boyfriend will be apart for 90,720 minutes (although it may seem like an eternity!).
The distance between the earth and the moon is about 250,000 miles. Convert this length to yards.
- Answer
-
440,000,000 yards
The astronauts of Expedition 28 on the International Space Station spend 15 weeks in space. Convert the time to minutes.
- Answer
-
151,200 minutes
How many ounces are in 1 gallon?
Solution
We will convert gallons to ounces by multiplying by several conversion factors. Refer to Table \(\PageIndex{1}\).
| 1 gallon | |
| Multiply the measurement to be converted by 1. | \(\frac{\text{1 gallon}}{\text{1}} \cdot \frac{\text{4 quarts}}{\text{1 gallon}} \cdot \frac{\text{2 pints}}{\text{1 quart}} \cdot \frac{\text{2 cups}}{\text{1 pint}} \cdot \frac{\text{8 ounces}}{\text{1 cup}}\) |
| Use conversion factors to get to the right unit. Simplify. |
 |
| Multiply. | \(\frac{1\cdot 4\cdot 2\cdot 2\cdot 8\text{ ounces}}{1\cdot 1\cdot 1\cdot 1\cdot 1 }\) |
| Simplify. | 128 ounces |
How many cups are in 1 gallon?
- Answer
-
16 cups
How many teaspoons are in 1 cup?
- Answer
-
48 teaspoons
Use Mixed Units of Measurement in the U.S. System
We often use mixed units of measurement in everyday situations. Suppose Joe is 5 feet 10 inches tall, stays at work for 7 hours and 45 minutes, and then eats a 1 pound 2 ounce steak for dinner—all these measurements have mixed units.
Performing arithmetic operations on measurements with mixed units of measures requires care. Be sure to add or subtract like units!
Seymour bought three steaks for a barbecue. Their weights were 14 ounces, 1 pound 2 ounces and 1 pound 6 ounces. How many total pounds of steak did he buy?
Solution
We will add the weights of the steaks to find the total weight of the steaks.
| Add the ounces. Then add the pounds. | 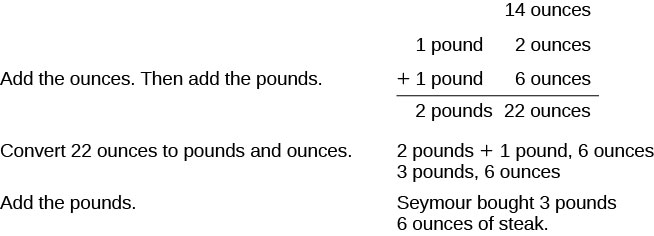 |
| Convert 22 ounces to pounds and ounces. | 2 pounds + 1 pound, 6 ounces |
| Add the pounds. | 3 pounds, 6 ounces |
| Seymour bought 3 pounds 6 ounces of steak. |
Laura gave birth to triplets weighing 3 pounds 3 ounces, 3 pounds 3 ounces, and 2 pounds 9 ounces. What was the total birth weight of the three babies?
- Answer
-
8 lbs. 15 oz
Stan cut two pieces of crown molding for his family room that were 8 feet 7 inches and 12 feet 11 inches. What was the total length of the molding?
- Answer
-
21 ft. 6 in.
Anthony bought four planks of wood that were each 6 feet 4 inches long. What is the total length of the wood he purchased?
Solution
We will multiply the length of one plank to find the total length.
| Multiply the inches and then the feet. | 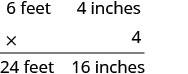 |
| Convert the 16 inches to feet. Add the feet. |
 |
| Anthony bought 25 feet and 4 inches of wood. |
Henri wants to triple his spaghetti sauce recipe that uses 1 pound 8 ounces of ground turkey. How many pounds of ground turkey will he need?
- Answer
-
4 lbs. 8 oz.
Joellen wants to double a solution of 5 gallons 3 quarts. How many gallons of solution will she have in all?
- Answer
-
11 gallons 2 qt.
Make Unit Conversions in the Metric System
In the metric system, units are related by powers of 10. The roots words of their names reflect this relation. For example, the basic unit for measuring length is a meter. One kilometer is 1,000 meters; the prefix kilo means thousand. One centimeter is \(\frac{1}{100}\) of a meter, just like one cent is \(\frac{1}{100}\) of one dollar.
The equivalencies of measurements in the metric system are shown in Table \(\PageIndex{2}\). The common abbreviations for each measurement are given in parentheses.
| Metric System of Measurement | ||
|---|---|---|
| Length | Mass | Capacity |
| 1 kilometer (km) = 1,000 m 1 hectometer (hm) = 100 m 1 dekameter (dam) = 10 m 1 meter (m) = 1 m 1 decimeter (dm) = 0.1 m 1 centimeter (cm) = 0.01 m 1 millimeter (mm) = 0.001 m |
1 kilogram (kg) = 1,000 g 1 hectogram (hg) = 100 g 1 dekagram (dag) = 10 g 1 gram (g) = 1 g 1 decigram (dg) = 0.1 g 1 centigram (cg) = 0.01 g 1 milligram (mg) = 0.001 g |
1 kiloliter (kL) = 1,000 L 1 hectoliter (hL) = 100 L 1 dekaliter (daL) = 10 L 1 liter (L) = 1 L 1 deciliter (dL) = 0.1 L 1 centiliter (cL) = 0.01 L 1 milliliter (mL) = 0.001 L |
| 1 meter = 100 centimeters 1 meter = 1,000 millimeters |
1 gram = 100 centigrams 1 gram = 1,000 milligrams |
1 liter = 100 centiliters 1 liter = 1,000 milliliters |
To make conversions in the metric system, we will use the same technique we did in the US system. Using the identity property of multiplication, we will multiply by a conversion factor of one to get to the correct units.
Have you ever run a 5K or 10K race? The length of those races are measured in kilometers. The metric system is commonly used in the United States when talking about the length of a race.
Nick ran a 10K race. How many meters did he run?
Solution
We will convert kilometers to meters using the identity property of multiplication.
| 10 kilometers | |
| Multiply the measurement to be converted by 1. |  |
| Write 1 as a fraction relating kilometers and meters. | 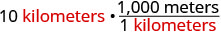 |
| Simplify. |  |
| Multiply. | 10,000 meters |
| Nick ran 10,000 meters. |
Sandy completed her first 5K race! How many meters did she run?
- Answer
-
5,000 meters
Herman bought a rug 2.5 meters in length. How many centimeters is the length?
- Answer
-
250 centimeters
Eleanor’s newborn baby weighed 3,200 grams. How many kilograms did the baby weigh?
Solution
We will convert grams into kilograms.
 |
|
| Multiply the measurement to be converted by 1. |  |
| Write 1 as a function relating kilograms and grams. | 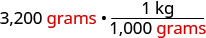 |
| Simplify. | 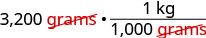 |
| Multiply. | \(\frac{3,200 \text{ kilograms}}{1,000}\) |
| Divide. | 3.2 kilograms The baby weighed 3.2 kilograms. |
Kari’s newborn baby weighed 2,800 grams. How many kilograms did the baby weigh?
- Answer
-
2.8 kilograms
Anderson received a package that was marked 4,500 grams. How many kilograms did this package weigh?
- Answer
-
4.5 kilograms
As you become familiar with the metric system you may see a pattern. Since the system is based on multiples of ten, the calculations involve multiplying by multiples of ten. We have learned how to simplify these calculations by just moving the decimal.
To multiply by 10, 100, or 1,000, we move the decimal to the right one, two, or three places, respectively. To multiply by 0.1, 0.01, or 0.001, we move the decimal to the left one, two, or three places, respectively.
We can apply this pattern when we make measurement conversions in the metric system. In Exercise \(\PageIndex{25}\), we changed 3,200 grams to kilograms by multiplying by \(\frac{1}{1000}\) (or 0.001). This is the same as moving the decimal three places to the left.
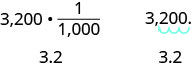
Convert
- 350 L to kiloliters
- 4.1 L to milliliters.
Solution
1. We will convert liters to kiloliters. In Table \(\PageIndex{2}\), we see that 1 kiloliter=1,000 liters.1kiloliter=1,000 liters.
| 350 L | |
| Multiply by 1, writing 1 as a fraction relating liters to kiloliters. | \(350 \text{ L}\frac{\text{1 kL}}{\text{1000L}}\) |
| Simplify. | \(350 \not{\text{ L}}\frac{\text{1 kL}}{1000 \not\text{ L}}\) |
 |
0.35 kL |
2. We will convert liters to milliliters. From Table \(\PageIndex{2}\) we see that 1 liter=1,000 milliliters.1 liter=1,000 milliliters.
 |
|
| Multiply by 1, writing 1 as a fraction relating liters to milliliters. | 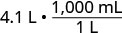 |
| Simplify. | 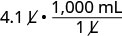 |
| Move the decimal 3 units to the right. | 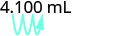 |
 |
Convert:
- 725 L to kiloliters
- 6.3 L to milliliters
- Answer
-
- 7,250 kiloliters
- 6,300 milliliters
Convert:
- 350 hL to liters
- 4.1 L to centiliters
- Answer
-
- 35,000 liters
- 410 centiliters
Use Mixed Units of Measurement in the Metric System
Performing arithmetic operations on measurements with mixed units of measures in the metric system requires the same care we used in the US system. But it may be easier because of the relation of the units to the powers of 10. Make sure to add or subtract like units.
Ryland is 1.6 meters tall. His younger brother is 85 centimeters tall. How much taller is Ryland than his younger brother?
Solution
We can convert both measurements to either centimeters or meters. Since meters is the larger unit, we will subtract the lengths in meters. We convert 85 centimeters to meters by moving the decimal 2 places to the left.
\[\begin{array} { cc } { \text {Write the } 85 \text { centimeters as meters. } } & { 1.60 \mathrm { m } } \\ {} &{ \dfrac { - 0.85 \mathrm { m } } { 0.75 \mathrm { m } } } \end{array}\]
Ryland is 0.75 m0.75 m taller than his brother.
Mariella is 1.58 meters tall. Her daughter is 75 centimeters tall. How much taller is Mariella than her daughter? Write the answer in centimeters.
- Answer
-
83 centimeters
The fence around Hank’s yard is 2 meters high. Hank is 96 centimeters tall. How much shorter than the fence is Hank? Write the answer in meters.
- Answer
-
1.04 meters
Dena’s recipe for lentil soup calls for 150 milliliters of olive oil. Dena wants to triple the recipe. How many liters of olive oil will she need?
Solution
We will find the amount of olive oil in milliliters then convert to liters.
\(\begin{array} { ll } {} & { \text { Triple } 150 \text{ mL}} \\ { \text { Translate to algebra. } } &{3\cdot 150 \text{ mL}} \\ { \text { Multiply. } } &{450\text{ mL}}\\ { \text { Convert to liters. } } &{450\cdot \frac{0.001\text{ L}}{1 \text{ ml}}} \\ { \text { Simplify. } } &{0.45 \text{ L}}\\ {} &{ \text { Dena needs 0.45 liters of olive oil. } } \end{array}\)
A recipe for Alfredo sauce calls for 250 milliliters of milk. Renata is making pasta with Alfredo sauce for a big party and needs to multiply the recipe amounts by 8. How many liters of milk will she need?
- Answer
-
2 liters
To make one pan of baklava, Dorothea needs 400 grams of filo pastry. If Dorothea plans to make 6 pans of baklava, how many kilograms of filo pastry will she need?
- Answer
-
2.4 kilograms
Convert Between the U.S. and the Metric Systems of Measurement
Many measurements in the United States are made in metric units. Our soda may come in 2-liter bottles, our calcium may come in 500-mg capsules, and we may run a 5K race. To work easily in both systems, we need to be able to convert between the two systems.
Table \(\PageIndex{3}\) shows some of the most common conversions.
| Conversion Factors Between U.S. and Metric Systems | ||
|---|---|---|
| Length | Mass | Capacity |
| \(\begin{array} { l l l } {1 \text{ in.}} & {=} &{2.54 \text{ cm}} \\ {1\text{ ft.}} &{=} &{0.305 \text{ m}} \\ {1 \text{ yd.}} & {=} &{0.914 \text{ m}} \\ {1\text{ mi.}} &{=} &{1.61 \text{ km}} \\ {1 \text{ m}} & {=} &{3.28 \text{ ft}} \end{array}\) | \(\begin{array} { l l l } {1 \text{ lb.}} & {=} &{0.45 \text{ kg}} \\ {1\text{ oz.}} &{=} &{28 \text{ g}} \\ {1 \text{ kg}} & {=} &{2.2 \text{ lb}} \end{array}\) | \(\begin{array} { l l l } {1 \text{ qt.}} & {=} &{0.95 \text{ L}} \\ {1\text{ fl. oz.}} &{=} &{30 \text{ ml}} \\ {1 \text{ L}} & {=} &{1.06 \text{ lb}} \end{array}\) |
Figure \(\PageIndex{3}\) shows how inches and centimeters are related on a ruler.

Figure \(\PageIndex{4}\) shows the ounce and milliliter markings on a measuring cup.
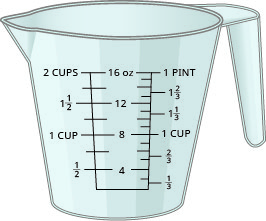
Figure \(\PageIndex{5}\) shows how pounds and kilograms marked on a bathroom scale.

We make conversions between the systems just as we do within the systems—by multiplying by unit conversion factors.
Lee’s water bottle holds 500 mL of water. How many ounces are in the bottle? Round to the nearest tenth of an ounce.
Solution
\(\begin{array} { l l } {} & {500 \text{ mL}} \\ {\text{Multiplying by a unit conversion factor relating}} &{500\text{ milliliters}\cdot\frac{1\text{ ounce}}{30\text{ milliliters}}} \\ {\text{mL and ounces}} &{} \\ {\text{Simplify.}} &{\frac{50\text{ ounce}}{30}} \\ {\text{Divide.}} &{16.7\text{ ounces}} \\ {} &{\text{The water bottle has 16.7 ounces}} \end{array}\)
How many quarts of soda are in a 2-L bottle?
- Answer
-
2.12 quarts
How many liters are in 4 quarts of milk?
- Answer
-
3.8 liters
Soleil was on a road trip and saw a sign that said the next rest stop was in 100 kilometers. How many miles until the next rest stop?
Solution
\(\begin{array} { l l } {} & {100 \text{ kilometers}} \\ {\text{Multiplying by a unit conversion factor relating}} &{100\text{ kilometers}\cdot\frac{1\text{ mile}}{1.61\text{ kilometers}}} \\ {\text{km and mi.}} &{} \\ {\text{Simplify.}} &{\frac{100\text{ miles}}{1.61}} \\ {\text{Divide.}} &{62\text{ miles}} \\ {} &{\text{Soleil will travel 62 miles.}} \end{array}\)
The height of Mount Kilimanjaro is 5,895 meters. Convert the height to feet.
- Answer
-
19,335.6 feet
The flight distance from New York City to London is 5,586 kilometers. Convert the distance to miles.
- Answer
-
3,469.57 miles
Convert between Fahrenheit and Celsius Temperatures
Have you ever been in a foreign country and heard the weather forecast? If the forecast is for 22°C, what does that mean?
The U.S. and metric systems use different scales to measure temperature. The U.S. system uses degrees Fahrenheit, written °F. The metric system uses degrees Celsius, written °C. Figure \(\PageIndex{6}\) shows the relationship between the two systems.
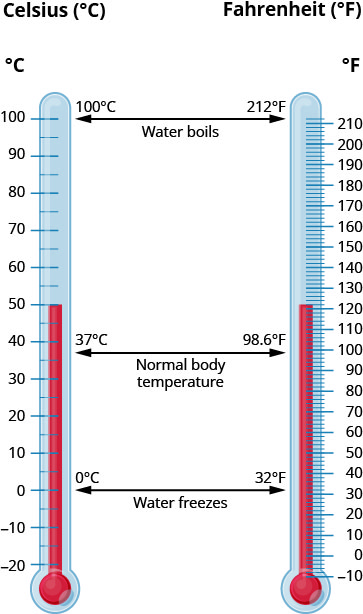
To convert from Fahrenheit temperature, F, to Celsius temperature, C, use the formula
\[C = \frac { 5 } { 9 } ( F - 32 )\]
To convert from Celsius temperature, C, to Fahrenheit temperature, F, use the formula
\[F = \frac { 9 } { 5 } C + 32\]
Convert 50° Fahrenheit into degrees Celsius.
Solution
We will substitute 50°F into the formula to find C.
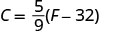 |
|
 |
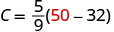 |
| Simplify in parentheses. | 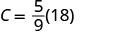 |
| Multiply. |  |
|
So we found that 50°F is equivalent to 10°C. |
Convert the Fahrenheit temperature to degrees Celsius: 59° Fahrenheit.
- Answer
-
15°C
Convert the Fahrenheit temperature to degrees Celsius: 41° Fahrenheit.
- Answer
-
5°C
While visiting Paris, Woody saw the temperature was 20° Celsius. Convert the temperature into degrees Fahrenheit.
Solution
We will substitute 20°C into the formula to find F.
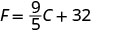 |
|
 |
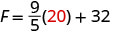 |
| Multiply. | 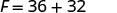 |
| Add. |  |
| So we found that 20°C is equivalent to 68°F. |
Convert the Celsius temperature to degrees Fahrenheit: the temperature in Helsinki, Finland, was 15° Celsius.
- Answer
-
59°F
Convert the Celsius temperature to degrees Fahrenheit: the temperature in Sydney, Australia, was 10° Celsius.
- Answer
-
50°F
Key Concepts
- Metric System of Measurement
- Length
1 kilometer (km) = 1,000 m
1 hectometer (hm) = 100 m
1 dekameter (dam) = 10 m
1 meter (m) = 1 m
1 decimeter (dm) = 0.1 m
1 centimeter (cm) = 0.01 m
1 millimeter (mm) = 0.001 m
1 meter = 100 centimeters
1 meter = 1,000 millimeters
- Mass
1 kilogram (kg) = 1,000 g
1 hectogram (hg) = 100 g
1 dekagram (dag) = 10 g
1 gram (g) = 1 g
1 decigram (dg) = 0.1 g
1 centigram (cg) = 0.01 g
1 milligram (mg) = 0.001 g
1 gram = 100 centigrams
1 gram = 1,000 milligrams
- Capacity
1 kiloliter (kL) = 1,000 L
1 hectoliter (hL) = 100 L
1 dekaliter (daL) = 10 L
1 liter (L) = 1 L
1 deciliter (dL) = 0.1 L
1 centiliter (cL) = 0.01 L
1 milliliter (mL) = 0.001 L
1 liter = 100 centiliters
1 liter = 1,000 milliliters
- Temperature Conversion
- To convert from Fahrenheit temperature, F, to Celsius temperature, C, use the formula \(C=\frac{5}{9}(F−32)\)
- To convert from Celsius temperature, C, to Fahrenheit temperature, F, use the formula \(F=\frac{9}{5}C+32\)


