2.6: Solve a Formula for a Specific Variable
- Page ID
- 15133
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Use the Distance, Rate, and Time formula
- Solve a formula for a specific variable
Before you get started, take this readiness quiz.
- Solve: \(15t=120\).
If you missed this problem, review Exercise 2.2.1. - Solve: \(6x+24=96\).
If you missed this problem, review Exercise 2.3.1.
Use the Distance, Rate, and Time Formula
One formula you will use often in algebra and in everyday life is the formula for distance traveled by an object moving at a constant rate. Rate is an equivalent word for “speed.” The basic idea of rate may already familiar to you. Do you know what distance you travel if you drive at a steady rate of 60 miles per hour for 2 hours? (This might happen if you use your car’s cruise control while driving on the highway.) If you said 120 miles, you already know how to use this formula!
For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula:
\[\begin{array} {lllll}{ d = r t} &{\text { where }} &{ d} &{=} &{\text{distance}} \\ {} &{} &{ r} &{=} &{\text{rate}} \\{} &{} &{ t} &{=} &{\text{time}} \end{array}\]
We will use the Strategy for Solving Applications that we used earlier in this chapter. When our problem requires a formula, we change Step 4. In place of writing a sentence, we write the appropriate formula. We write the revised steps here for reference.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. Write the appropriate formula for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
You may want to create a mini-chart to summarize the information in the problem. See the chart in this first example.
Jamal rides his bike at a uniform rate of 12 miles per hour for \(3\frac{1}{2}\) hours. What distance has he traveled?
Solution
| Step 1. Read the problem. | ||
| Step 2. Identify what you are looking for. | distance traveled | |
| Step 3. Name. Choose a variable to represent it. | Let d = distance. | |
| Step 4. Translate: Write the appropriate formula. | \(d=rt\) | |
 |
||
| Substitute in the given information. | \(d = 12\cdot 3\frac{1}{2}\) | |
| Step 5. Solve the equation. | \(d=42\text{ miles}\) | |
| Step 6. Check | ||
| Does 42 miles make sense? | ||
| Jamal rides: | ||
 |
||
| Step 7. Answer the question with a complete sentence. | Jamal rode 42 miles. | |
Lindsay drove for \(5\frac{1}{2}\) hours at 60 miles per hour. How much distance did she travel?
- Answer
-
330 miles
Trinh walked for \(2\frac{1}{3}\) hours at 3 miles per hour. How far did she walk?
- Answer
-
7 miles
Rey is planning to drive from his house in San Diego to visit his grandmother in Sacramento, a distance of 520 miles. If he can drive at a steady rate of 65 miles per hour, how many hours will the trip take?
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | How many hours (time) |
| Step 3. Name. Choose a variable to represent it. |
Let t = time. |
 |
|
| Step 4. Translate. Write the appropriate formula. |
\(d=rt\) |
| Substitute in the given information. | \(520 = 65t\) |
| Step 5. Solve the equation. | \(t = 8\) |
| Step 6. Check. Substitute the numbers into the formula and make sure the result is a true statement. |
|
| \(\begin{array}{lll} {d} &{=} &{rt} \\ {520} &{\stackrel{?}{=}} &{65\cdot 8}\\ {520} &{=} &{520\checkmark} \end{array}\) | |
| Step 7. Answer the question with a complete sentence. Rey’s trip will take 8 hours. | |
Lee wants to drive from Phoenix to his brother’s apartment in San Francisco, a distance of 770 miles. If he drives at a steady rate of 70 miles per hour, how many hours will the trip take?
- Answer
-
11 hours
Yesenia is 168 miles from Chicago. If she needs to be in Chicago in 3 hours, at what rate does she need to drive?
- Answer
-
56 mph
Solve a Formula for a Specific Variable
You are probably familiar with some geometry formulas. A formula is a mathematical description of the relationship between variables. Formulas are also used in the sciences, such as chemistry, physics, and biology. In medicine they are used for calculations for dispensing medicine or determining body mass index. Spreadsheet programs rely on formulas to make calculations. It is important to be familiar with formulas and be able to manipulate them easily.
In Exercise \(\PageIndex{1}\) and Exercise \(\PageIndex{4}\), we used the formula \(d=rt\). This formula gives the value of d, distance, when you substitute in the values of r and t, the rate and time. But in Exercise \(\PageIndex{4}\), we had to find the value of t. We substituted in values of d and r and then used algebra to solve for tt. If you had to do this often, you might wonder why there is not a formula that gives the value of t when you substitute in the values of d and r. We can make a formula like this by solving the formula \(d=rt\) for t.
To solve a formula for a specific variable means to isolate that variable on one side of the equals sign with a coefficient of 1. All other variables and constants are on the other side of the equals sign. To see how to solve a formula for a specific variable, we will start with the distance, rate and time formula.
Solve the formula d=rt for t:
- when d=520 and r=65
- in general
Solution
We will write the solutions side-by-side to demonstrate that solving a formula in general uses the same steps as when we have numbers to substitute.
| 1. when d=520 and r=65 | 2. in general | ||
| Write the formula. | \(d=rt\) | Write the formula. | \(d=rt\) |
| Substitute. | \(520=65t\) | ||
| Divide, to isolate t. | \(\frac{520}{65} = \frac{65t}{65}\) | Divide, to isolate tt. | \(\frac{d}{r} = \frac{rt}{t}\) |
| Simplify. | \(8 = t\) | Simplify. | \(\frac{d}{r}=t\) |
We say the formula \(t = \frac{d}{r}\) is solved for t.
Solve the formula \(d=rt\) for r:
- when d=180 and t=4
- in general
- Answer
-
- \(r = 45\)
- \(r = \frac{d}{t}\)
Solve the formula \(d=rt\) for r:
- when d=780 and t=12
- in general
- Answer
-
- \(r = 65\)
- \(r = \frac{d}{rt\)
Solve the formula \(A = \frac{1}{2}bh\) for h:
- when \(A = 90\) and \(b = 15\)
- in general
Solution
| 1. when \(A = 90\) and \(b = 15\) | 2. in general | ||
| Write the formula. | 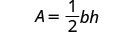 |
Write the formula. | 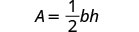 |
| Substitute. | 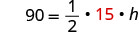 |
||
| Clear the fractions. | 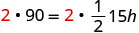 |
Clear the fractions. | 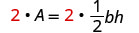 |
| Simplify. | 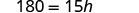 |
Simplify. | 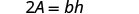 |
| Solve for h. | 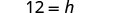 |
Solve for hh. | 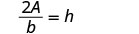 |
Solve the formula \(A = \frac{1}{2}bh\) for h:
- when \(A = 170\) and \(b = 17\)
- in general
- Answer
-
- \(h = 20\)
- \(h = \frac{2A}{b}\)
Solve the formula \(A = \frac{1}{2}bh\) for h:
- when \(A = 62\) and \(h = 31\)
- in general
- Answer
-
- \(b = 4\)
- \(b = \frac{2A}{h}\)
The formula \(I=Prt\) is used to calculate simple interest, I, for a principal, P, invested at rate, r, for t years.
Solve the formula I=Prt to find the principal, P:
- when I=$5,600, r=4% ,t=7years
- in general
Solution
| 1. I=$5,600, r=4% ,t=7years | 2. in general | ||
| Write the formula. | 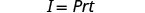 |
Write the formula. | 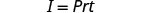 |
| Substitute. | 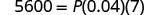 |
||
| Simplify. | 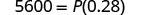 |
Simplify. | 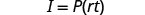 |
| Divide, to isolate P. | 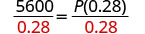 |
Divide, to isolate P. |  |
| Simplify. | 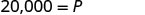 |
Simplify. | 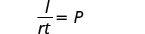 |
| The principal is | 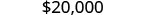 |
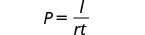 |
|
Solve the formula I=Prt to find the principal, P:
- when I=$2160, r=6% ,t=3 years
- in general
- Answer
-
- $12000
- \(P = \frac{1}{rt}\)
Solve the formula I=Prt to find the principal, P:
- when I=$5400, r= 12% ,t=5 years
- in general
- Answer
-
- $9000
- \(P = \frac{1}{rt}\)
Later in this class, and in future algebra classes, you’ll encounter equations that relate two variables, usually x and y. You might be given an equation that is solved for y and need to solve it for x, or vice versa. In the following example, we’re given an equation with both x and y on the same side and we’ll solve it for y.
Solve the formula 3x+2y=18 for y:
- when x=4
- in general
Solution
| 1. when x=4 | 2. in general | ||
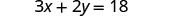 |
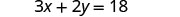 |
||
| Substitute. | 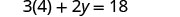 |
||
| Subtract to isolate the y-term. |
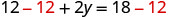 |
Subtract to isolate the y-term. |
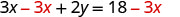 |
| Divide. | 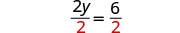 |
Divide. | 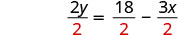 |
| Simplify. | 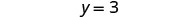 |
Simplify. | 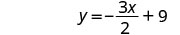 |
Solve the formula 3x+4y=10 for y:
- when \(x = \frac{14}{3}\)
- in general
- Answer
-
- \(y = -1\)
- \(y = \frac{10 - 3x}{4}\)
Solve the formula 5x+2y=18 for y:
- when \(x = 4\)
- in general
- Answer
-
- \(y = -1\)
- \(y = \frac{18 - 5x}{2}\)
In Exercise \(\PageIndex{7}\) through Exercise \(\PageIndex{18}\) we used the numbers in part 1 as a guide to solving in general in part 2. Now we will solve a formula in general without using numbers as a guide.
Solve the formula P=a+b+c for a.
Solution
| We will isolate aa on one side of the equation. | 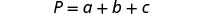 |
| Both b and c are added to a, so we subtract them from both sides of the equation. | 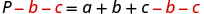 |
| Simplify. |  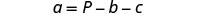 |
Solve the formula P=a+b+c for b.
- Answer
-
b=P−a−c
Solve the formula P=a+b+c for c.
- Answer
-
c=P−a−b
Solve the formula 6x+5y=13 for y.
Solution
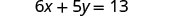 |
|
| Subtract 6x from both sides to isolate the term with y. | 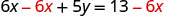 |
| Simplify. | 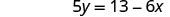 |
| Divide by 5 to make the coefficient 1. | 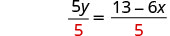 |
| Simplify. | 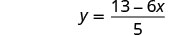 |
The fraction is simplified. We cannot divide 13−6x by 5.
Solve the formula 4x+7y=9 for y.
- Answer
-
\(y = \frac{9 - 4x}{7}\)
Solve the formula 5x+8y=1 for y.
- Answer
-
\(y = \frac{1 - 5x}{8}\)
Key Concepts
- To Solve an Application (with a formula)
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. Write the appropriate formula for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
- Distance, Rate and Time
For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula: d=rt where d = distance, r = rate, t = time. - To solve a formula for a specific variable means to get that variable by itself with a coefficient of 1 on one side of the equation and all other variables and constants on the other side.


