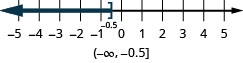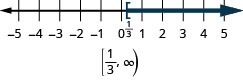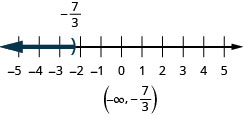2.7E: Exercises

Last updated
Save as PDF

Page ID: 30112

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Graph Inequalities on the Number Line

In the following exercises, graph each inequality on the number line

Exercise $\PageIndex{1}$

$x\leq 2$
x>−1
x<0

Exercise $\PageIndex{2}$

x>1
x<−2
$x\geq −3$

Answer

$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is greater than 1 is graphed on the number line, with an open parenthesis at x equals 1, and a dark line extending to the right of the parenthesis.$
$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is less than negative 2 is graphed on the number line, with an open parenthesis at x equals negative 2, and a dark line extending to the left of the parenthesis.$
$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is greater than or equal to negative 3 is graphed on the number line, with an open bracket at x equals negative 3, and a dark line extending to the right of the bracket.$

Exercise $\PageIndex{3}$

$x\geq −3$
x<4
$x\leq −2$

Exercise $\PageIndex{4}$

$x\leq 0$
x>−4
$x\geq −1$

Answer

$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is less than or equal to 0 is graphed on the number line, with an open bracket at x equals 0, and a dark line extending to the left of the bracket.$
$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is greater than negative 4 is graphed on the number line, with an open parenthesis at x equals negative 4, and a dark line extending to the right of the parenthesis.$
$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is greater than or equal to negative 1 is graphed on the number line, with an open bracket at x equals negative 1, and a dark line extending to the right of the bracket.$

In the following exercises, graph each inequality on the number line and write in interval notation.

Exercise $\PageIndex{5}$

x<−2
$x\geq −3.5$
$ x\leq \frac{2}{3}$

Exercise $\PageIndex{6}$

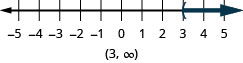
$x>3$
$x \leq-0.5$
$x \geq \frac{1}{3}$

Answer

$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is greater than 3 is graphed on the number line, with an open parenthesis at x equals 3, and a dark line extending to the right of the parenthsis. Below the number line is the solution written in interval notation: parenthesis, 3 comma infinity, parenthesis.$
$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is less than or equal to negative 0.5 is graphed on the number line, with an open bracket at x equals negative 0.5, and a dark line extending to the left of the bracket. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma negative 0.5, bracket.$
$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is greater than or equal to 1/3 is graphed on the number line, with an open bracket at x equals 1/3 (written in), and a dark line extending to the right of the bracket. Below the number line is the solution written in interval notation: bracket, 1/3 comma infinity, parenthesis.$

Exercise $\PageIndex{7}$

$x \geq-4$
x<2.5
$x>-\frac{3}{2}$

Exercise $\PageIndex{8}$

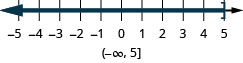
$x\leq 5$
$x\geq −1.5x$
x<−73

Answer

$This figure is a number line with tick marks. The inequality x is less than or equal to 5 is graphed on the number line, with an open bracket at x equals 5, and a dark line extending to the left of the bracket. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma 5, bracket.$
$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is greater than or equal to negative 1.5 is graphed on the number line, with an open bracket at x equals negative 1.5, and a dark line extending to the right of the bracket. Below the number line is the solution written in interval notation: bracket, negative 1.5 comma infinity, parenthesis.$
$This figure is a number line ranging from negative 5 to 5 with tick marks for each integer. The inequality x is less than negative 7/3 is graphed on the number line, with an open parenthesis at x equals negative 7/3 (written in), and a dark line extending to the left of the parenthsis. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma negative 7/3, parenthesis.$

Solve Inequalities using the Subtraction and Addition Properties of Inequality

In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.

Exercise $\PageIndex{9}$

$n-11<33$

Exercise $\PageIndex{10}$

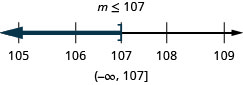
$m-45 \leq 62$

Answer: $At the top of this figure is the solution to the inequality: m is less than or equal to 107. Below this is a number line ranging from 105 to 109 with tick marks for each integer. The inequality x is less than or equal to 107 is graphed on the number line, with an open bracket at x equals 107, and a dark line extending to the left of the bracket. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma 107, bracket.$

Exercise $\PageIndex{11}$

$u+25>21$

Exercise $\PageIndex{12}$

$v+12>3$

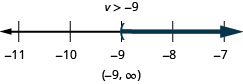
Answer: $At the top of this figure is the solution to the inequality: v is greater than negative 9. Below this is a number line ranging from negative 11 to negative 7 with tick marks for each integer. The inequality x is greater than negative 9 is graphed on the number line, with an open parenthesis at x equals negative 9, and a dark line extending to the right of the parenthesis. Below the number line is the solution written in interval notation: parenthesis, negative 9 comma infinity, parenthesis.$

Exercise $\PageIndex{13}$

$a+\frac{3}{4} \geq \frac{7}{10}$

Exercise $\PageIndex{14}$

$b+\frac{7}{8} \geq \frac{1}{6}$

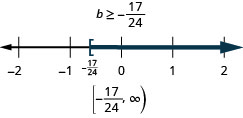
Answer: $At the top of this figure is the solution to the inequality: b is greater than or equal to negative 17/24. Below this is a number line ranging from negative 2 to 2 with tick marks for each integer. The inequality b is greater than or equal to negative 17/24 is graphed on the number line, with an open bracket at b equals negative 17/24 (written in), and a dark line extending to the right of the bracket. Below the number line is the solution written in interval notation: bracket, negative 17/24 comma infinity, parenthesis.$

Exercise $\PageIndex{15}$

$f-\frac{13}{20}<-\frac{5}{12}$

Exercise $\PageIndex{16}$

$g-\frac{11}{12}<-\frac{5}{18}$

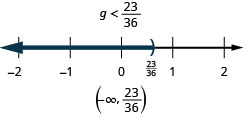
Answer: $At the top of this figure is the solution to the inequality: g is less than 23/26. Below this is a number line ranging from negative 2 to 2 with tick marks for each integer. The inequality g is less than 23/26 is graphed on the number line, with an open parenthesis at g equals 23/26 (written in), and a dark line extending to the left of the parenthesis. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma 23/26, parenthesis.$

Solve Inequalities using the Division and Multiplication Properties of Inequality

In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.

Exercise $\PageIndex{17}$

$8 x>72$

Exercise $\PageIndex{18}$

$6 y<48$

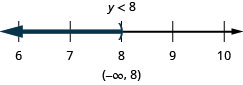
Answer: $At the top of this figure is the solution to the inequality: y is less than 8. Below this is a number line ranging from 6 to 10 with tick marks for each integer. The inequality y is less than 8 is graphed on the number line, with an open parenthesis at y equals 8, and a dark line extending to the left of the parenthesis. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma 8, parenthesis.$

Exercise $\PageIndex{19}$

$7 r \leq 56$

Exercise $\PageIndex{20}$

$9 s \geq 81$

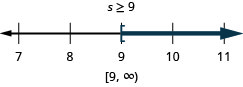
Answer: $At the top of this figure is the solution to the inequality: s is greater than or equal to 9. Below this is a number line ranging from 7 to 11 with tick marks for each integer. The inequality s is greater than or equal to 9 is graphed on the number line, with an open bracket at s equals 9, and a dark line extending to the right of the bracket. Below the number line is the solution written in interval notation: bracket, 9 comma infinity, parenthesis.$

Exercise $\PageIndex{21}$

$-5 u \geq 65$

Exercise $\PageIndex{22}$

$-8 v \leq 96$

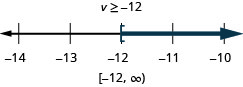
Answer: $At the top of this figure is the solution to the inequality: v is greater than or equal to negative 12. Below this is a number line ranging from negative 14 to negative 10 with tick marks for each integer. The inequality v is greater than or equal to negative 12 is graphed on the number line, with an open bracket at v equals negative 12, and a dark line extending to the right of the bracket. Below the number line is the solution written in interval notation: bracket, negative 12 comma infinity, parenthesis.$

Exercise $\PageIndex{23}$

$-9 c<126$

Exercise $\PageIndex{24}$

$-7 d>105$

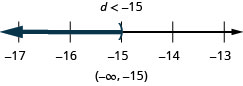
Answer: $At the top of this figure is the solution to the inequality: d is less than negative 15. Below this is a number line ranging from negative 17 to negative 13 with tick marks for each integer. The inequality d is less than negative 15 is graphed on the number line, with an open parenthesis at d equals negative 15, and a dark line extending to the left of the parenthesis. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma negative 15, parenthesis.$

Exercise $\PageIndex{25}$

$20>\frac{2}{5} h$

Exercise $\PageIndex{26}$

$40<\frac{5}{8} k$

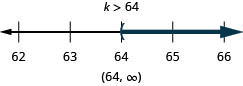
Answer: $At the top of this figure is the solution to the inequality: k is greater than 64. Below this is a number line ranging from 62 to 66 with tick marks for each integer. The inequality k is greater than 64 is graphed on the number line, with an open parenthesis at k equals 64, and a dark line extending to the right of the parenthesis. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma 64, parenthesis.$

Exercise $\PageIndex{27}$

$\frac{7}{6} j \geq 42$

Exercise $\PageIndex{28}$

$\frac{9}{4} g \leq 36$

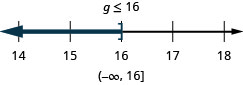
Answer: $At the top of this figure is the solution to the inequality: g is less than or equal to 16. Below this is a number line ranging from 14 to 18 with tick marks for each integer. The inequality g is less than or equal to 16 is graphed on the number line, with an open bracket at g equals 16, and a dark line extending to the left of the bracket. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma 16, bracket.$

Exercise $\PageIndex{29}$

$\frac{a}{-3} \leq 9$

Exercise $\PageIndex{30}$

$\frac{b}{-10} \geq 30$

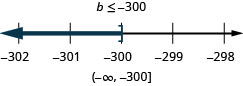
Answer: $At the top of this figure is the solution to the inequality: b is less than or equal to negative 300. Below this is a number line ranging from negative 302 to negative 298 with tick marks for each integer. The inequality b is less than or equal to negative 300 is graphed on the number line, with an open bracket at b equals negative 300, and a dark line extending to the left of the bracket. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma negative 300, bracket.$

Exercise $\PageIndex{31}$

$-25<\frac{p}{-5}$

Exercise $\PageIndex{32}$

$-18>\frac{q}{-6}$

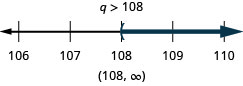
Answer: $At the top of this figure is the solution to the inequality: q is greater than 108. Below this is a number line ranging from 106 to 110 with tick marks for each integer. The inequality q is greater than 108 is graphed on the number line, with an open parenthesis at q equals 108, and a dark line extending to the right of the parenthesis. Below the number line is the solution written in interval notation: parenthesis, 108 comma infinity, parenthesis.$

Exercise $\PageIndex{33}$

$9 t \geq-27$

Exercise $\PageIndex{34}$

$7 s<-28$

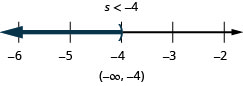
Answer: $At the top of this figure is the solution to the inequality: s is less than negative 4. Below this is a number line ranging from negative 6 to negative 2 with tick marks for each integer. The inequality s is less than negative 4 is graphed on the number line, with an open parenthesis at s equals negative 4, and a dark line extending to the left of the parenthesis. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma negative 4, parenthesis.$

Exercise $\PageIndex{35}$

$\frac{2}{3} y>-36$

Exercise $\PageIndex{36}$

$\frac{3}{5} x \leq-45$

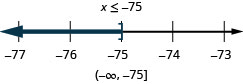
Answer: $At the top of this figure is the solution to the inequality: x is less than or equal to negative 75. Below this is a number line ranging from negative 77 to negative 73 with tick marks for each integer. The inequality x is less than or equal to negative 75 is graphed on the number line, with an open bracket at x equals negative 75, and a dark line extending to the left of the bracket. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma negative 75, bracket.$

Solve Inequalities That Require Simplification

In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.

Exercise $\PageIndex{37}$

$4 v \geq 9 v-40$

Exercise $\PageIndex{38}$

$5 u \leq 8 u-21$

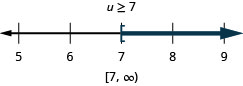
Answer: $At the top of this figure is the solution to the inequality: au is greater than or equal to 7. Below this is a number line ranging from 5 to 9 with tick marks for each integer. The inequality u is greater than or equal to 7 is graphed on the number line, with an open bracket at u equals 7, and a dark line extending to the right of the bracket. Below the number line is the solution written in interval notation: bracket, 7 comma infinity, parenthesis.$

Exercise $\PageIndex{39}$

$13 q<7 q-29$

Exercise $\PageIndex{40}$

$9 p>14 p-18$

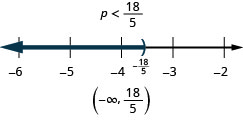
Answer: $At the top of this figure is the solution to the inequality: p is less than 18/5. Below this is a number line ranging from 2 to 6 with tick marks for each integer. The inequality p is less than 18/5 is graphed on the number line, with an open parenthesis at p equals 18/5 (written in), and a dark line extending to the left of the parenthesis. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma 18/5, parenthesis.$

Exercise $\PageIndex{41}$

$12 x+3(x+7)>10 x-24$

Exercise $\PageIndex{42}$

$9 y+5(y+3)<4 y-35$

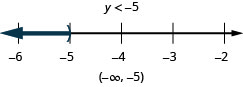
Answer: $At the top of this figure is the solution to the inequality: y is less than negative 5. Below this is a number line ranging from negative 6 to negative 2 with tick marks for each integer. The inequality y is less than negative 5 is graphed on the number line, with an open parenthesis at y equals negative 5, and a dark line extending to the left of the parenthesis. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma negative 5, parenthesis.$

Exercise $\PageIndex{43}$

$6 h-4(h-1) \leq 7 h-11$

Exercise $\PageIndex{44}$

$4 k-(k-2) \geq 7 k-26$

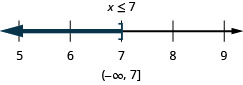
Answer: $At the top of this figure is the solution to the inequality: x is less than or equal to 7. Below this is a number line ranging from 5 to 9 with tick marks for each integer. The inequality x is less than or equal to 7 is graphed on the number line, with an open bracket at x equals 7, and a dark line extending to the left of the bracket. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma 7, bracket.$

Exercise $\PageIndex{45}$

$8 m-2(14-m) \geq 7(m-4)+3 m$

Exercise $\PageIndex{46}$

$6 n-12(3-n) \leq 9(n-4)+9 n$

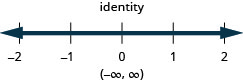
Answer: $At the top of this figure is the solution to the inequality: the inequality is an identity. Below this is a number line ranging from negative 2 to 2 with tick marks for each integer. The identity is graphed on the number line, with a dark line extending in both directions. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma infinity, parenthesis.$

Exercise $\PageIndex{47}$

$\frac{3}{4} b-\frac{1}{3} b<\frac{5}{12} b-\frac{1}{2}$

Exercise $\PageIndex{48}$

$9 u+5(2 u-5) \geq 12(u-1)+7 u$

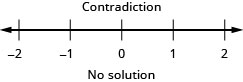
Answer: $At the top of this figure is the result of the inequality: the inequality is a contradiction. Below this is a number line ranging from negative 2 to 2 with tick marks for each integer. Because this is a contradiction, no inequality is graphed on the number line. Below the number line is the statement: “No solution”.$

Exercise $\PageIndex{49}$

$\frac{2}{3} g-\frac{1}{2}(g-14) \leq \frac{1}{6}(g+42)$

Exercise $\PageIndex{50}$

$\frac{5}{6} a-\frac{1}{4} a>\frac{7}{12} a+\frac{2}{3}$

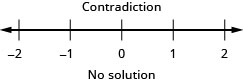
Answer: $At the top of this figure is the result of the inequality: the inequality is a contradiction. Below this is a number line ranging from negative 2 to 2 with tick marks for each integer. Because this is a contradiction, no inequality is graphed on the number line. Below the number line is the statement: “No solution”.$

Exercise $\PageIndex{51}$

$\frac{4}{5} h-\frac{2}{3}(h-9) \geq \frac{1}{15}(2 h+90)$

Exercise $\PageIndex{52}$

$12 v+3(4 v-1) \leq 19(v-2)+5 v$

Answer: $At the top of this figure is the result of the inequality: the inequality is a contradiction. Below this is a number line ranging from negative 2 to 2 with tick marks for each integer. Because this is a contradiction, no inequality is graphed on the number line. Below the number line is the statement: “No solution”.$

Mixed practice

In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.

Exercise $\PageIndex{53}$

$15 k \leq-40$

Exercise $\PageIndex{54}$

$35 k \geq-77$

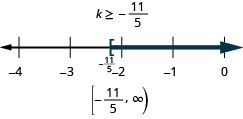
Answer: $At the top of this figure is the solution to the inequality: k is greater than or equal to negative 11/5. Below this is a number line ranging from negative 4 to 0 with tick marks for each integer. The inequality k is greater than or equal to negative 11/5 is graphed on the number line, with an open bracket at k equals negative 11/5 (written in), and a dark line extending to the right of the bracket. Below the number line is the solution written in interval notation: bracket, negative 11/5 comma infinity, parenthesis.$

Exercise $\PageIndex{55}$

$23 p-2(6-5 p)>3(11 p-4)$

Exercise $\PageIndex{56}$

$18 q-4(10-3 q)<5(6 q-8)$

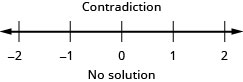
Answer: $At the top of this figure is the result of the inequality: the inequality is a contradiction. Below this is a number line ranging from negative 2 to 2 with tick marks for each integer. Because this is a contradiction, no inequality is graphed on the number line. Below the number line is the statement: “No solution”.$

Exercise $\PageIndex{57}$

$-\frac{9}{4} x \geq-\frac{5}{12}$

Exercise $\PageIndex{58}$

$-\frac{21}{8} y \leq-\frac{15}{28}$

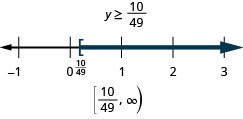
Answer: $At the top of this figure is the solution to the inequality: y is greater than or equal to 10/49. Below this is a number line ranging from negative 1 to 3 with tick marks for each integer. The inequality y is greater than or equal to 10/49 is graphed on the number line, with an open bracket at y equals 10/49 (written in), and a dark line extending to the right of the bracket. Below the number line is the solution written in interval notation: bracket, 10/49 comma infinity, parenthesis.$

Exercise $\PageIndex{59}$

$c+34<-99$

Exercise $\PageIndex{60}$

$d+29>-61$

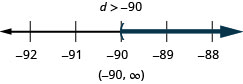
Answer: $At the top of this figure is the solution to the inequality: d is greater than negative 90. Below this is a number line ranging from negative 92 to negative 88 with tick marks for each integer. The inequality d is greater than negative 90 is graphed on the number line, with an open parenthesis at d equals negative 90, and a dark line extending to the right of the parenthesis. Below the number line is the solution written in interval notation: parenthesis, negative 90 comma infinity, parenthesis.$

Exercise $\PageIndex{61}$

$\frac{m}{18} \geq-4$

Exercise $\PageIndex{62}$

$\frac{n}{13} \leq-6$

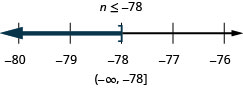
Answer: $At the top of this figure is the solution to the inequality: n is less than or equal to negative 78. Below this is a number line ranging from negative 80 to negative 76 with tick marks for each integer. The inequality n is less than or equal to negative 78 is graphed on the number line, with an open bracket at n equals negative 78, and a dark line extending to the left of the bracket. Below the number line is the solution written in interval notation: parenthesis, negative infinity comma negative 78, bracket.$

Translate to an Inequality and Solve

In the following exercises, translate and solve .Then write the solution in interval notation and graph on the number line.

Exercise $\PageIndex{63}$

Fourteen times d is greater than 56.

Exercise $\PageIndex{64}$

Ninety times c is less than 450.

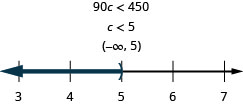
Answer: $At the top of this figure is the the inequality 90c is less than 450. Below this is the solution to the inequality: c is less than 5. Below the solution is the solution written in interval notation: parenthesis, negative infinity comma 5, parenthesis. Below the interval notation is a number line ranging from 3 to 7 with tick marks for each integer. The inequality c is less than 5 is graphed on the number line, with an open parenthesis at c equals 5, and a dark line extending to the left of the parenthesis.$

Exercise $\PageIndex{65}$

Eight times $z$ is smaller than $-40$

Exercise $\PageIndex{66}$

Ten times $y$ is at most $-110$

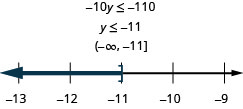
Answer: $At the top of this figure is the the inequality 10y is less than or equal to negative 110. Below this is the solution to the inequality: y is less than or equal to negative 11. Below the solution is the solution written in interval notation: parenthesis, negative infinity comma negative 11, bracket. Below the interval notation is a number line ranging from negative 13 to negative 9 with tick marks for each integer. The inequality y is less than or equal to negative 11 is graphed on the number line, with an open bracket at y equals negative 11, and a dark line extending to the left of the bracket.$

Exercise $\PageIndex{67}$

Three more than $h$ is no less than 25

Exercise $\PageIndex{68}$

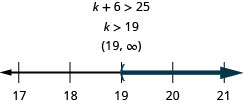
Six more than $k$ exceeds 25

Answer: $At the top of this figure is the the inequality k plus 6 is greater than 25. Below this is the solution to the inequality: k is greater than 19. Below the the solution written in interval notation: parenthesis, 19 comma infinity, parenthesis. Below the interval notation is a number line ranging from 17 to 21 with tick marks for each integer. The inequality k is greater than 19 is graphed on the number line, with an open parenthesis at k equals 19, and a dark line extending to the right of the parenthesis.$

Exercise $\PageIndex{69}$

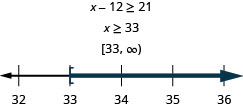
Ten less than $w$ is at least $39 .$

Exercise $\PageIndex{70}$

Twelve less than $x$ is no less than 21

Answer: $At the top of this figure is the the inequality x minus 12 is greater than or equal to 21. Below this is the solution to the inequality: x is greater than or equal to 33. Below the solution is the solution written in interval notation: bracket, 33 comma infinity, parenthesis. Below the interval notation is a number line ranging from 32 to 36 with tick marks for each integer. The inequality x is greater than or equal to 33 is graphed on the number line, with an open bracket at x equals 33, and a dark line extending to the right of the bracket.$

Exercise $\PageIndex{71}$

Negative five times $r$ is no more than $95 .$

Exercise $\PageIndex{72}$

Negative two times s is lower than 56

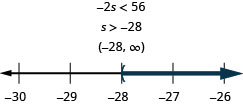
Answer: $At the top of this figure is the the inequality negative 2s is less than 56. Below this is the solution to the inequality: s is greater than negative 28. Below the solution is the solution written in interval notation: parenthesis, negative 28 comma infinity, parenthesis. Below the interval notation is a number line ranging from negative 30 to negative 26 with tick marks for each integer. The inequality s is greater than negative 28 is graphed on the number line, with an open parenthesis at s equals negative 28, and a dark line extending to the right of the parenthesis.$

Exercise $\PageIndex{73}$

Nineteen less than $b$ is at most $-22$

Exercise $\PageIndex{74}$

Fifteen less than a is at least $-7$

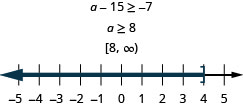
Answer: $At the top of this figure is the the inequality a minus 15 is greater than or equal to negative 7. Below this is the solution to the inequality: a is greater than or equal to 8. Below the solution is the solution written in interval notation: bracket, 8 comma infinity, parenthesis. Below the interval notation is a number line ranging from 0 to 10 with tick marks for each integer. The inequality a is greater than or equal to 8 is graphed on the number line, with an open bracket at a equals 8, and a dark line extending to the right of the bracket.$

Everyday Math

Exercise $\PageIndex{75}$

Safety A child’s height, h, must be at least 57 inches for the child to safely ride in the front seat of a car. Write this as an inequality.

Exercise $\PageIndex{76}$

Fighter pilots The maximum height, h, of a fighter pilot is 77 inches. Write this as an inequality.

Answer: $h \leq 77$

Exercise $\PageIndex{77}$

Elevators The total weight, w, of an elevator’s passengers can be no more than 1,200 pounds. Write this as an inequality.

Exercise $\PageIndex{78}$

Shopping The number of items, n, a shopper can have in the express check-out lane is at most 8. Write this as an inequality.

Answer: $n \leq 8$

Writing Exercises

Exercise $\PageIndex{79}$

Give an example from your life using the phrase ‘at least’.

Exercise $\PageIndex{80}$

Give an example from your life using the phrase ‘at most’.

Answer: Answers will vary.

Exercise $\PageIndex{81}$

Explain why it is necessary to reverse the inequality when solving $-5 x>10$

Exercise $\PageIndex{82}$

Explain why it is necessary to reverse the inequality when solving $\frac{n}{-3}<12$

Answer: Answers will vary.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$This is a table that has six rows and four columns. In the first row, which is a header row, the cells read from left to right: “I can…,” “confidently,” “with some help,” and “no-I don’t get it!” The first column below “I can…” reads “graph inequalities on the number line,” “solve inequalitites using the Subtraction and Addition Properties of Inequality,” “solve inequalitites using the Division and Multiplication Properties of Inequality,” “solve inequalities that require simplification,” and “translate to an inequality and solve.” The rest of the cells are blank.$

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

Practice Makes Perfect

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)

Exercise \(\PageIndex{18}\)

Exercise \(\PageIndex{19}\)

Exercise \(\PageIndex{20}\)

Exercise \(\PageIndex{21}\)

Exercise \(\PageIndex{22}\)

Exercise \(\PageIndex{23}\)

Exercise \(\PageIndex{24}\)

Exercise \(\PageIndex{25}\)

Exercise \(\PageIndex{26}\)

Exercise \(\PageIndex{27}\)

Exercise \(\PageIndex{28}\)

Exercise \(\PageIndex{29}\)

Exercise \(\PageIndex{30}\)

Exercise \(\PageIndex{31}\)

Exercise \(\PageIndex{32}\)

Exercise \(\PageIndex{33}\)

Exercise \(\PageIndex{34}\)

Exercise \(\PageIndex{35}\)

Exercise \(\PageIndex{36}\)

Exercise \(\PageIndex{37}\)

Exercise \(\PageIndex{38}\)

Exercise \(\PageIndex{39}\)

Exercise \(\PageIndex{40}\)

Exercise \(\PageIndex{41}\)

Exercise \(\PageIndex{42}\)

Exercise \(\PageIndex{43}\)

Exercise \(\PageIndex{44}\)

Exercise \(\PageIndex{45}\)

Exercise \(\PageIndex{46}\)

Exercise \(\PageIndex{47}\)

Exercise \(\PageIndex{48}\)

Exercise \(\PageIndex{49}\)

Exercise \(\PageIndex{50}\)

Exercise \(\PageIndex{51}\)

Exercise \(\PageIndex{52}\)

Exercise \(\PageIndex{53}\)

Exercise \(\PageIndex{54}\)

Exercise \(\PageIndex{55}\)

Exercise \(\PageIndex{56}\)

Exercise \(\PageIndex{57}\)

Exercise \(\PageIndex{58}\)

Exercise \(\PageIndex{59}\)

Exercise \(\PageIndex{60}\)

Exercise \(\PageIndex{61}\)

Exercise \(\PageIndex{62}\)

Exercise \(\PageIndex{63}\)

Exercise \(\PageIndex{64}\)

Exercise \(\PageIndex{65}\)

Exercise \(\PageIndex{66}\)

Exercise \(\PageIndex{67}\)

Exercise \(\PageIndex{68}\)

Exercise \(\PageIndex{69}\)

Exercise \(\PageIndex{70}\)

Exercise \(\PageIndex{71}\)

Exercise \(\PageIndex{72}\)

Exercise \(\PageIndex{73}\)

Exercise \(\PageIndex{74}\)

Everyday Math

Exercise \(\PageIndex{75}\)

Exercise \(\PageIndex{76}\)

Exercise \(\PageIndex{77}\)

Exercise \(\PageIndex{78}\)