4.4: Understanding the Slope of a Line
- Page ID
- 15146
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- By the end of this section, you will be able to:
- Use geoboards to model slope
- Use \(m = \frac{\text{rise}}{\text{run}}\) to find the slope of a line from its graph
- Find the slope of horizontal and vertical lines
- Use the slope formula to find the slope of a line between two points
- Graph a line given a point and the slope
- Solve slope applications
Before you get started, take this readiness quiz.
- Simplify: \(\frac{1 - 4}{8 - 2}\).
If you missed this problem, review Exercise 1.6.31 - Divide: \(\frac{0}{4}, \frac{4}{0}\).
If you missed this problem, review Exercise 1.10.16. - Simplify: \(\frac{15}{-3}, \frac{-15}{3}, \frac{-15}{-3}\).
If you missed this problem, review Exercise 1.6.4.
When you graph linear equations, you may notice that some lines tilt up as they go from left to right and some lines tilt down. Some lines are very steep and some lines are flatter. What determines whether a line tilts up or down or if it is steep or flat?
In mathematics, the ‘tilt’ of a line is called the slope of the line. The concept of slope has many applications in the real world. The pitch of a roof, grade of a highway, and a ramp for a wheelchair are some examples where you literally see slopes. And when you ride a bicycle, you feel the slope as you pump uphill or coast downhill.
In this section, we will explore the concept of slope.
Use Geoboards to Model Slope
A geoboard is a board with a grid of pegs on it. Using rubber bands on a geoboard gives us a concrete way to model lines on a coordinate grid. By stretching a rubber band between two pegs on a geoboard, we can discover how to find the slope of a line.
Doing the Manipulative Mathematics activity “Exploring Slope” will help you develop a better understanding of the slope of a line. (Graph paper can be used instead of a geoboard, if needed.)
We’ll start by stretching a rubber band between two pegs as shown in Figure \(\PageIndex{1}\).
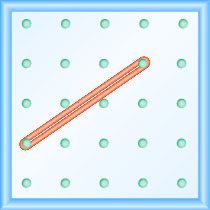
Doesn’t it look like a line?
Now we stretch one part of the rubber band straight up from the left peg and around a third peg to make the sides of a right triangle, as shown in Figure \(\PageIndex{2}\)
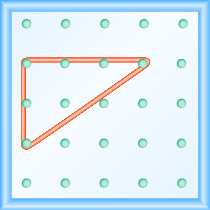
We carefully make a 90º angle around the third peg, so one of the newly formed lines is vertical and the other is horizontal.
To find the slope of the line, we measure the distance along the vertical and horizontal sides of the triangle. The vertical distance is called the rise and the horizontal distance is called the run, as shown in Figure \(\PageIndex{3}\).
If our geoboard and rubber band look just like the one shown in Figure \(\PageIndex{4}\), the rise is 2. The rubber band goes up 2 units. (Each space is one unit.)
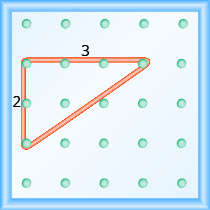
The rise on this geoboard is 2, as the rubber band goes up two units.
What is the run?
The rubber band goes across 3 units. The run is 3 (see Figure \(\PageIndex{4}\)).
The slope of a line is the ratio of the rise to the run. In mathematics, it is always referred to with the letter m.
The slope of a line of a line is \(m = \frac{\text{rise}}{\text{run}}\).
The rise measures the vertical change and the run measures the horizontal change between two points on the line.
What is the slope of the line on the geoboard in Figure \(\PageIndex{4}\)?
\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{2}{3} \end{aligned}\]
The line has slope \(\frac{2}{3}\). This means that the line rises 2 units for every 3 units of run.
When we work with geoboards, it is a good idea to get in the habit of starting at a peg on the left and connecting to a peg to the right. If the rise goes up it is positive and if it goes down it is negative. The run will go from left to right and be positive.
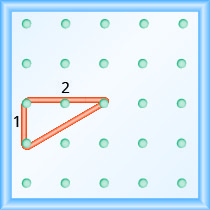
What is the slope of the line on the geoboard shown?
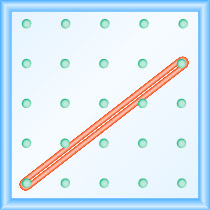
Solution
Use the definition of slope: \(m = \frac{\text{rise}}{\text{run}}\).
Start at the left peg and count the spaces up and to the right to reach the second peg.
\[\begin{array}{ll} {\text { The rise is } 3 .} &{m=\frac{3}{\operatorname{run}}} \\ {\text { The run is 4. }} & {m=\frac{3}{4}} \\ { } & {\text { The slope is } \frac{3}{4} \text { . }}\end{array}\]
This means that the line rises 3 units for every 4 units of run.
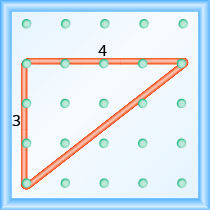
What is the slope of the line on the geoboard shown?
- Answer
-
\(\frac{4}{3}\)
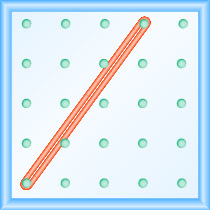
What is the slope of the line on the geoboard shown?
- Answer
-
\(\frac{1}{4}\)
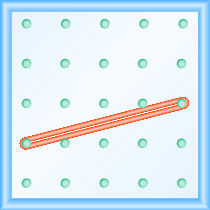
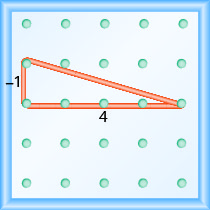
What is the slope of the line on the geoboard shown?
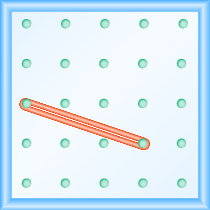
Solution
Use the definition of slope: \(m = \frac{\text{rise}}{\text{run}}\).
Start at the left peg and count the units down and to the right to reach the second peg.
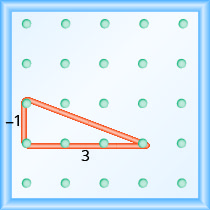
\[\begin{array}{ll}{\text { The rise is }-1 .} & {m=\frac{-1}{\operatorname{run}}} \\ {\text { The run is } 3 .} & {m=\frac{-1}{3}} \\ {} & {m=-\frac{1}{3}} \\ {} &{\text { The slope is }-\frac{1}{3}}\end{array}\]
This means that the line drops 1 unit for every 3 units of run.
What is the slope of the line on the geoboard?
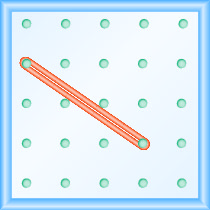
- Answer
-
\(-\frac{2}{3}\)
What is the slope of the line on the geoboard?
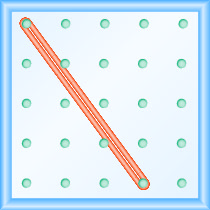
- Answer
-
\(-\frac{4}{3}\)
Notice that in Exercise \(\PageIndex{1}\) the slope is positive and in Exercise \(\PageIndex{4}\) the slope is negative. Do you notice any difference in the two lines shown in Figure(a) and Figure(b)?
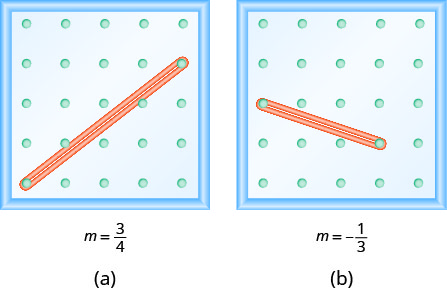
We ‘read’ a line from left to right just like we read words in English. As you read from left to right, the line in Figure(a) is going up; it has positive slope. The line in Figure(b) is going down; it has negative slope.

Use a geoboard to model a line with slope \(\frac{1}{2}\).
Solution
To model a line on a geoboard, we need the rise and the run.
\(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{1}{2} \text { . }} &{ \frac{1}{2} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } 1 \text { and the run is } 2 \text { . }} \\ {\text { Start at a peg in the lower left of the geoboard. }} \\ {\text { Stretch the rubber band up } 1 \text { unit, and then right } 2 \text { units. }}\end{array}\)
The hypotenuse of the right triangle formed by the rubber band represents a line whose slope is \(\frac{1}{2}\).
Model the slope \(m = \frac{1}{3}\). Draw a picture to show your results.
- Answer
-
Model the slope \(m = \frac{3}{2}\). Draw a picture to show your results.
- Answer
-

Use a geoboard to model a line with slope \(\frac{-1}{4}\).
Solution
Use the slope formula. m = \( \frac{\text{rise}}{\text{run}} \).
Replace \(m\) with \( \frac{-1}{4} \).
So, the rise is \(-1\) and the run is \(4\).
Since the rise is negative, we choose a starting peg on the upper left that will give us room to count down.
We stretch the rubber band down \(1\) unit, and then right \(4\) units.
The hypotenuse of the right triangle formed by the rubber band represents a line whose slope is \(\frac{-1}{4}\).
Model the slope \(m = -2 = \frac{-2}{1}\). Draw a picture to show your results.
- Answer
-
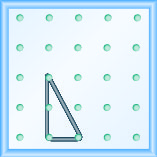
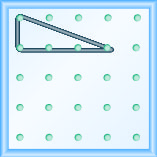
Model the slope \(m = \frac{-1}{3}\). Draw a picture to show your results.
- Answer
-
Use \(m = \frac{\text{rise}}{\text{run}}\) to Find the Slope of a Line from its Graph
Now, we’ll look at some graphs on the xy-coordinate plane and see how to find their slopes. The method will be very similar to what we just modeled on our geoboards.
To find the slope, we must count out the rise and the run. But where do we start?
We locate two points on the line whose coordinates are integers. We then start with the point on the left and sketch a right triangle, so we can count the rise and run.
Find the slope of the line shown.
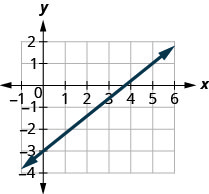
Solution



Find the slope of the line shown.
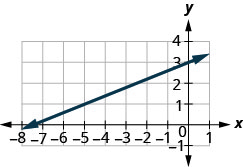
- Answer
-
\(\frac{2}{5}\)
Find the slope of the line shown.
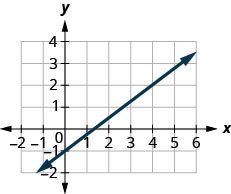
- Answer
-
\(\frac{3}{4}\)
- Locate two points on the line whose coordinates are integers.
- Starting with the point on the left, sketch a right triangle, going from the first point to the second point.
- Count the rise and the run on the legs of the triangle.
- Take the ratio of rise to run to find the slope, \(m = \frac{\text{rise}}{\text{run}}\).
Find the slope of the line shown.
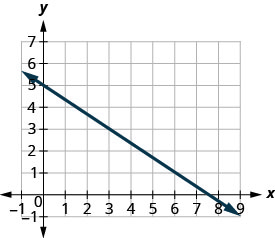
Solution
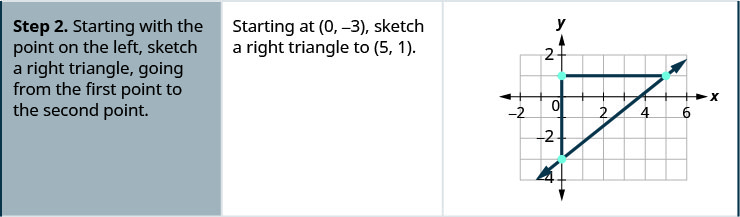
| Locate two points on the graph whose coordinates are integers. | (0,5) and (3,3) |
| Which point is on the left? | (0,5) |
| Starting at (0,5), sketch a right triangle to (3,3). | 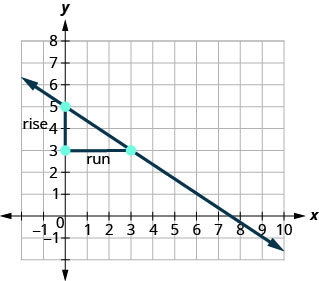 |
| Count the rise—it is negative. | The rise is −2. |
| Count the run. | The run is 3. |
| Use the slope formula. | \(m = \frac{\text{rise}}{\text{run}}\) |
| Substitute the values of the rise and run. | \(m = \frac{-2}{3}\) |
| Simplify. | \(m = -\frac{2}{3}\) |
| The slope of the line is \(-\frac{2}{3}\). |
So y increases by 3 units as x decreases by 2 units.
What if we used the points (−3,7) and (6,1) to find the slope of the line?
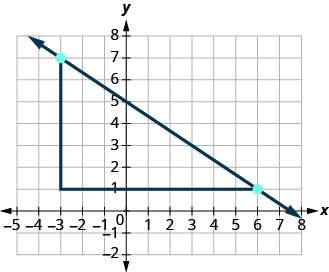
The rise would be −6 and the run would be 9. Then \(m = \frac{-6}{9}\), and that simplifies to \(m = -\frac{2}{3}\). Remember, it does not matter which points you use—the slope of the line is always the same.
Find the slope of the line shown.
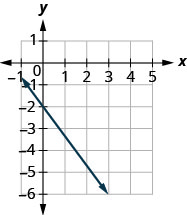
- Answer
-
\(-\frac{4}{3}\)
Find the slope of the line shown.
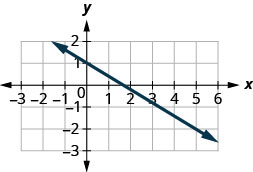
- Answer
-
\(-\frac{3}{5}\)
In the last two examples, the lines had y-intercepts with integer values, so it was convenient to use the y-intercept as one of the points to find the slope. In the next example, the y-intercept is a fraction. Instead of using that point, we’ll look for two other points whose coordinates are integers. This will make the slope calculations easier.
Find the slope of the line shown.
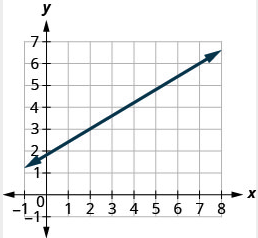
Solution
| Locate two points on the graph whose coordinates are integers. | (2,3) and (7,6) |
| Which point is on the left? | (2,3) |
| Starting at (2,3), sketch a right triangle to (7,6). | 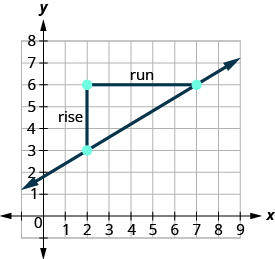 |
| Count the rise. | The rise is 3. |
| Count the run. | The run is 5. |
| Use the slope formula. | \(m = \frac{\text{rise}}{\text{run}}\) |
| Substitute the values of the rise and run. | \(m = \frac{3}{5}\) |
| The slope of the line is \(\frac{3}{5}\). |
This means that y increases 5 units as x increases 3 units.
When we used geoboards to introduce the concept of slope, we said that we would always start with the point on the left and count the rise and the run to get to the point on the right. That way the run was always positive and the rise determined whether the slope was positive or negative.
What would happen if we started with the point on the right?
Let’s use the points (2,3) and (7,6) again, but now we’ll start at (7,6).
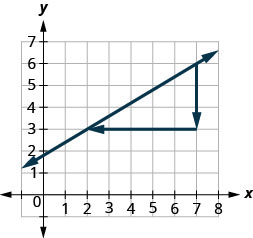
\(\begin{array}{ll} {\text {Count the rise.}} &{\text{The rise is −3.}} \\ {\text {Count the run. It goes from right to left, so}} &{\text {The run is−5.}} \\{\text{it is negative.}} &{}\\ {\text {Use the slope formula.}} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{Substitute the values of the rise and run.}} &{m = \frac{-3}{-5}} \\{} &{\text{The slope of the line is }\frac{3}{5}}\\ \end{array}\)
It does not matter where you start—the slope of the line is always the same.
Find the slope of the line shown.
- Answer
-
\(\frac{5}{4}\)
Find the slope of the line shown.
- Answer
-
\(\frac{3}{2}\)
Find the Slope of Horizontal and Vertical Lines
Do you remember what was special about horizontal and vertical lines? Their equations had just one variable.
\[\begin{array}{ll}{\textbf {Horizontal line } y=b} & {\textbf {Vertical line } x=a} \\ {y \text { -coordinates are the same. }} & {x \text { -coordinates are the same. }}\end{array}\]
So how do we find the slope of the horizontal line y=4? One approach would be to graph the horizontal line, find two points on it, and count the rise and the run. Let’s see what happens when we do this.
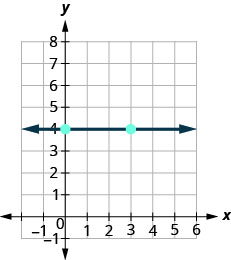
\(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 0.}} \\ {\text {What is the run?}} & {\text {The run is 3.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {} &{m = \frac{0}{3}} \\ {\text{What is the slope?}} &{m = 0} \\ {} &{\text{The slope of the horizontal line y = 4 is 0.}} \end{array}\)
All horizontal lines have slope 0. When the y-coordinates are the same, the rise is 0.
The slope of a horizontal line, y=b, is 0.
The floor of your room is horizontal. Its slope is 0. If you carefully placed a ball on the floor, it would not roll away.
Now, we’ll consider a vertical line, the line.
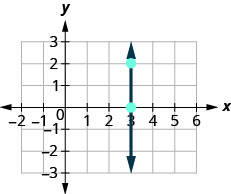
\(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 2.}} \\ {\text {What is the run?}} & {\text {The run is 0.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{What is the slope?}} &{m = \frac{2}{0}} \end{array}\)
But we can’t divide by 0. Division by 0 is not defined. So we say that the slope of the vertical line x=3 is undefined.
The slope of any vertical line is undefined. When the x-coordinates of a line are all the same, the run is 0.
The slope of a vertical line, x=a, is undefined.
Find the slope of each line:
(a) x=8 (b) y=−5.
Solution
(a) x=8
This is a vertical line.
Its slope is undefined.
(b) y=−5
This is a horizontal line.
It has slope 0.
Find the slope of the line: x=−4.
- Answer
-
undefined
Find the slope of the line: y=7.
- Answer
-
0
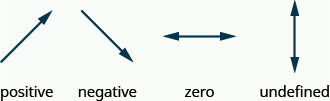
Remember, we ‘read’ a line from left to right, just like we read written words in English.
Use the Slope Formula to find the Slope of a Line Between Two Points
Doing the Manipulative Mathematics activity “Slope of Lines Between Two Points” will help you develop a better understanding of how to find the slope of a line between two points.
Sometimes we’ll need to find the slope of a line between two points when we don’t have a graph to count out the rise and the run. We could plot the points on grid paper, then count out the rise and the run, but as we’ll see, there is a way to find the slope without graphing. Before we get to it, we need to introduce some algebraic notation.
We have seen that an ordered pair (x,y) gives the coordinates of a point. But when we work with slopes, we use two points. How can the same symbol (x,y) be used to represent two different points? Mathematicians use subscripts to distinguish the points.
\[\begin{array}{ll}{\left(x_{1}, y_{1}\right)} & {\text { read }^{‘} x \text { sub } 1, y \text { sub } 1^{'}} \\ {\left(x_{2}, y_{2}\right)} & {\text { read }^{‘} x \text { sub } 2, y \text { sub } 2^{’}}\end{array}\]
The use of subscripts in math is very much like the use of last name initials in elementary school. Maybe you remember Laura C. and Laura M. in your third grade class?
We will use \(\left(x_{1}, y_{1}\right)\) to identify the first point and \(\left(x_{2}, y_{2}\right)\) to identify the second point.
If we had more than two points, we could use \(\left(x_{3}, y_{3}\right)\), \(\left(x_{4}, y_{4}\right)\), and so on.
Let’s see how the rise and run relate to the coordinates of the two points by taking another look at the slope of the line between the points (2,3) and (7,6).
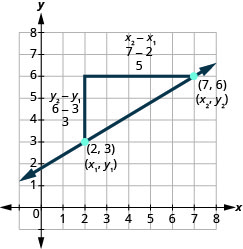
Since we have two points, we will use subscript notation, \(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {2,3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {7,6}\end{array}\right)\).
On the graph, we counted the rise of 3 and the run of 5.
Notice that the rise of 3 can be found by subtracting the y-coordinates 6 and 3.
\[3=6-3\]
And the run of 5 can be found by subtracting the x-coordinates 7 and 2.
\[5 = 7 - 2\]
We know \(m = \frac{\text{rise}}{\text{run}}\). So \(m = \frac{3}{5}\).
We rewrite the rise and run by putting in the coordinates \(m = \frac{6-3}{7-2}\)
But 6 is \(y_{2}\), the y-coordinate of the second point and 3 is \(y_{1}\), the y-coordinate of the first point.
So we can rewrite the slope using subscript notation. \(m = \frac{y2-y1}{7-2}\)
Also, 7 is \(x_{2}\), the x-coordinate of the second point and 2 is \(x_{1}\), the x-coordinate of the first point.
So, again, we rewrite the slope using subscript notation. \(m = \frac{y2-y1}{x2-x1}\)
We’ve shown that \(m = \frac{y2-y1}{x2-x1}\) is really another version of \(m = \frac{\text{rise}}{\text{run}}\). We can use this formula to find the slope of a line when we have two points on the line.
The slope of the line between two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is
\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]
This is the slope formula.
The slope is:
\[\begin{array}{c}{y \text { of the second point minus } y \text { of the first point }} \\ {\text { over }} \\ {x \text { of the second point minus } x \text { of the first point. }}\end{array}\]
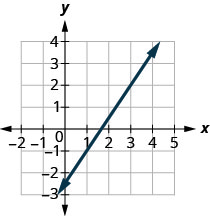
Use the slope formula to find the slope of the line between the points (1,2) and (4,5).
Solution
\(\begin{array} {ll} {\text{We’ll call (1,2) point #1 and (4,5) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {1,2}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {4,5}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{5-2}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{5-2}{4-1}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{3}{3}} \\{\text{Simplify.}} &{m = 1} \end{array}\)
Let’s confirm this by counting out the slope on a graph using \(m = \frac{\text{rise}}{\text{run}}\).
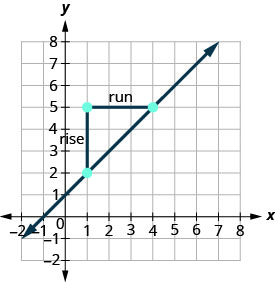
It doesn’t matter which point you call point #1 and which one you call point #2. The slope will be the same. Try the calculation yourself.
Use the slope formula to find the slope of the line through the points: (8,5) and (6,3).
- Answer
-
1
Use the slope formula to find the slope of the line through the points: (1,5) and (5,9).
- Answer
-
1
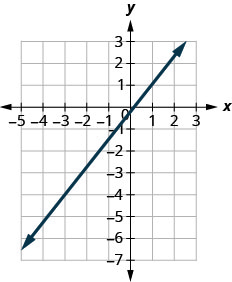
Use the slope formula to find the slope of the line through the points (−2,−3) and (−7,4).
Solution
\(\begin{array} {ll} {\text{We’ll call (-2, -3) point #1 and (-7,4) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-2,-3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-7,4}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{4-(-3)}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{7}{-5}} \\{\text{Simplify.}} &{m = -\frac{7}{5}} \end{array}\)
Let’s verify this slope on the graph shown.
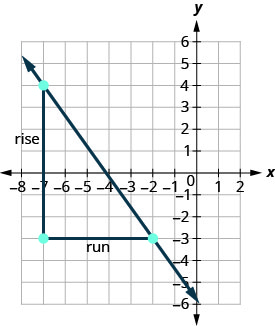
\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{-7}{5} \\ m &=-\frac{7}{5} \end{aligned}\]
Use the slope formula to find the slope of the line through the points: (−3,4) and (2,−1).
- Answer
-
-1
Use the slope formula to find the slope of the line through the pair of points: (−2,6) and (−3,−4).
- Answer
-
10
Graph a Line Given a Point and the Slope
Up to now, in this chapter, we have graphed lines by plotting points, by using intercepts, and by recognizing horizontal and vertical lines.
One other method we can use to graph lines is called the point–slope method. We will use this method when we know one point and the slope of the line. We will start by plotting the point and then use the definition of slope to draw the graph of the line.
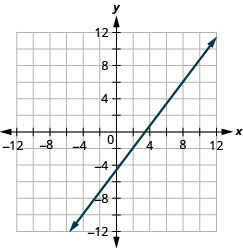
Graph the line passing through the point (1,−1) whose slope is \(m = \frac{3}{4}\).
Solution




Graph the line passing through the point (2,−2) with the slope \(m = \frac{4}{3}\).
- Answer
-
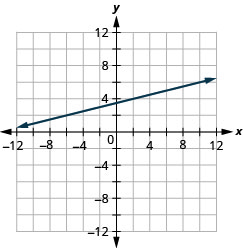
Graph the line passing through the point (−2,3) with the slope \(m=\frac{1}{4}\).
- Answer
-
- Plot the given point.
- Use the slope formula \(m=\frac{\text { rise }}{\text { rise }}\) to identify the rise and the run.
- Starting at the given point, count out the rise and run to mark the second point.
- Connect the points with a line.
Graph the line with y-intercept 2 whose slope is \(m=−\frac{2}{3}\).
Solution
Plot the given point, the y-intercept, (0,2).
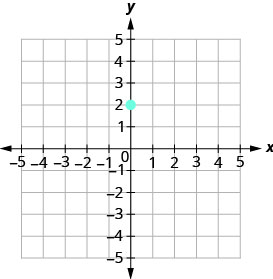
\(\begin{array} {ll} {\text{Identify the rise and the run.}} &{m =-\frac{2}{3}} \\ {} &{\frac{\text { rise }}{\text { run }} =\frac{-2}{3} }\\ {}&{\text { rise } =-2} \\ {} &{\text { run } =3} \end{array}\)
Count the rise and the run. Mark the second point.
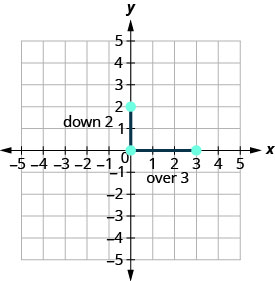
Connect the two points with a line.
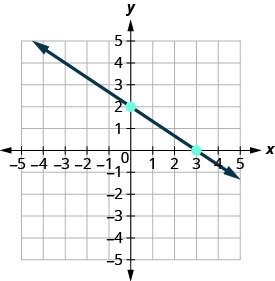
You can check your work by finding a third point. Since the slope is \(m=−\frac{2}{3}\), it can be written as \(m=\frac{2}{-3}\). Go back to (0,2) and count out the rise, 2, and the run, −3.
Graph the line with the y-intercept 4 and slope \(m=−\frac{5}{2}\).
- Answer
-
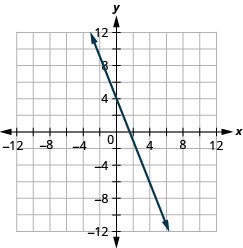
Graph the line with the x-intercept −3 and slope \(m=−\frac{3}{4}\).
- Answer
-
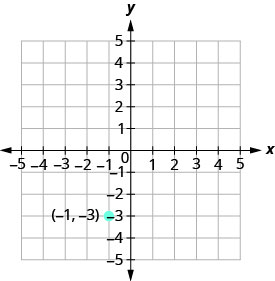
Graph the line passing through the point (−1,−3) whose slope is m=4.
Solution
Plot the given point.
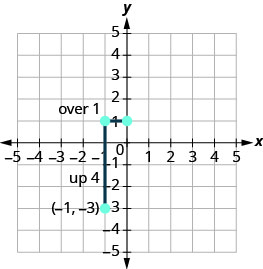
\(\begin{array} {ll} {\text{Identify the rise and the run.}} &{ \text{ m = 4}} \\ {\text{Write 4 as a fraction.}} &{\frac{\text {rise}}{\text {run}} =\frac{4}{1} }\\ {}&{\text {rise} =4\quad\text {run} =1} \end{array}\)
Count the rise and run and mark the second point.
Connect the two points with a line.
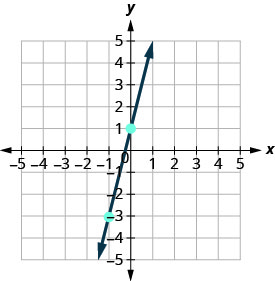
You can check your work by finding a third point. Since the slope is m=4, it can be written as \(m = \frac{-4}{-1}\). Go back to (−1,−3) and count out the rise, −4, and the run, −1.
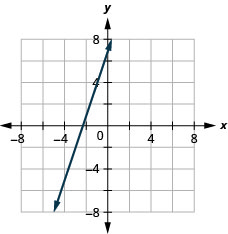
Graph the line with the point (−2,1) and slope m=3.
- Answer
-
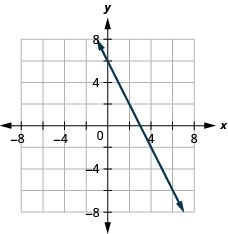
Graph the line with the point (4,−2) and slope m=−2.
- Answer
-
Solve Slope Applications
At the beginning of this section, we said there are many applications of slope in the real world. Let’s look at a few now.
The ‘pitch’ of a building’s roof is the slope of the roof. Knowing the pitch is important in climates where there is heavy snowfall. If the roof is too flat, the weight of the snow may cause it to collapse. What is the slope of the roof shown?
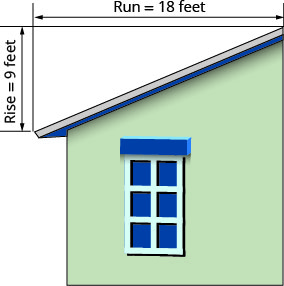
Solution
\(\begin{array}{ll}{\text { Use the slope formula. }} & {m=\frac{\text { rise }}{\text { rise }}} \\ {\text { Substitute the values for rise and run. }} & {m=\frac{9}{18}} \\ {\text { Simplify. }} & {m=\frac{1}{2}}\\ {\text{The slope of the roof is }\frac{1}{2}.} &{} \\ {} &{\text{The roof rises 1 foot for every 2 feet of}} \\ {} &{\text{horizontal run.}} \end{array}\)
Use Exercise \(\PageIndex{40}\), substituting the rise = 14 and run = 24.
- Answer
-
\(\frac{7}{12}\)
Use Exercise \(\PageIndex{40}\), substituting rise = 15 and run = 36.
- Answer
-
\(\frac{5}{12}\)
Have you ever thought about the sewage pipes going from your house to the street? They must slope down \(\frac{1}{4}\) inch per foot in order to drain properly. What is the required slope?

Solution
\(\begin{array} {ll} {\text{Use the slope formula.}} &{m=\frac{\text { rise }}{\text { run }}} \\ {} &{m=\frac{-\frac{1}{4} \mathrm{inch}}{1 \text { foot }}}\\ {}&{m=\frac{-\frac{1}{4} \text { inch }}{12 \text { inches }}} \\ {\text{Simplify.}} &{m=-\frac{1}{48}} \\{} &{\text{The slope of the pipe is }-\frac{1}{48}} \end{array}\)
The pipe drops 1 inch for every 48 inches of horizontal run.
Find the slope of a pipe that slopes down \(\frac{1}{3}\) inch per foot.
- Answer
-
\(-\frac{1}{36}\)
Find the slope of a pipe that slopes down \(\frac{3}{4}\) inch per yard.
- Answer
-
\(-\frac{1}{48}\)
Access these online resources for additional instruction and practice with understanding slope of a line.
- Practice Slope with a Virtual Geoboard
- Small, Medium, and Large Virtual Geoboards
- Explore Area and Perimeter with a Geoboard
Key Concepts
- Find the Slope of a Line from its Graph using \(m=\frac{\text { rise }}{\text { run }}\)
- Locate two points on the line whose coordinates are integers.
- Starting with the point on the left, sketch a right triangle, going from the first point to the second point.
- Count the rise and the run on the legs of the triangle.
- Take the ratio of rise to run to find the slope.
- Graph a Line Given a Point and the Slope
- Plot the given point.
- Use the slope formula \(m=\frac{\text { rise }}{\text { run }}\) to identify the rise and the run.
- Starting at the given point, count out the rise and run to mark the second point.
- Connect the points with a line.
- Slope of a Horizontal Line
- The slope of a horizontal line, y=b, is 0.
- Slope of a vertical line
- The slope of a vertical line, x=a, is undefined


