8.4: Add and Subtract Rational Expressions with Unlike Denominators
- Page ID
- 15176
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Find the least common denominator of rational expressions
- Find equivalent rational expressions
- Add rational expressions with different denominators
- Subtract rational expressions with different denominators
Before you get started, take this readiness quiz.
If you miss a problem, go back to the section listed and review the material.
- Add: \(\frac{7}{10}+\frac{8}{15}\).
If you missed this problem, review Exercise 1.7.13. - Subtract: \(6(2x+1)−4(x−5)\).
If you missed this problem, review Exercise 1.10.52. - Find the Greatest Common Factor of \(9x^{2}y^{3}\) and \(12xy^{5}\)
If you missed this problem, review Exercise 7.1.7. - Factor completely −48n−12
If you missed this problem, review Exercise 7.1.31.
Find the Least Common Denominator of Rational Expressions
When we add or subtract rational expressions with unlike denominators we will need to get common denominators. If we review the procedure we used with numerical fractions, we will know what to do with rational expressions.
Let’s look at the example \(\frac{7}{12}+\frac{5}{18}\) from Foundations. Since the denominators are not the same, the first step was to find the least common denominator (LCD). Remember, the LCD is the least common multiple of the denominators. It is the smallest number we can use as a common denominator.
To find the LCD of 12 and 18, we factored each number into primes, lining up any common primes in columns. Then we “brought down” one prime from each column. Finally, we multiplied the factors to find the LCD.
12=2·2·3
18=2·3·3
LCD=2·2·3·3
LCD=36
We do the same thing for rational expressions. However, we leave the LCD in factored form.
- Factor each expression completely.
- List the factors of each expression. Match factors vertically when possible.
- Bring down the columns.
- Multiply the factors.
Remember, we always exclude values that would make the denominator zero. What values of xvshould we exclude in this next example?
Find the LCD for \(\frac{8}{x^2−2x−3}\),\(\frac{3x}{x^2+4x+3}\)
- Answer
-
\(\frac{8}{x^2−2x−3}\),\(\frac{3x}{x^2+4x+3}\) Factor each expression completely, lining up common factors. Bring down the columns. \(x^2−2x−3=(x−3)(x+1)\) \(x^2+4x+3=(x+1)(x+3)\) Multiply the factors. LCD=(x+1)(x−3)(x+3) The LCD is (x+1)(x−3)(x+3).
Find the LCD for \(\frac{2}{x^2−x−12},\frac{1}{x^2−16}\)
- Answer
-
(x−4)(x+4)(x+3)
Find the LCD for \(\frac{x}{x^2+8x+15},\frac{5}{x^2+9x+18}\)
- Answer
-
(x+3)(x+6)(x+5)
Find Equivalent Rational Expressions
When we add numerical fractions, once we find the LCD, we rewrite each fraction as an equivalent fraction with the LCD.
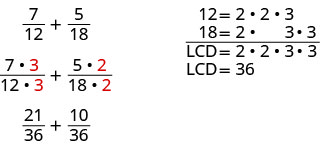
We will do the same thing for rational expressions.
Rewrite as equivalent rational expressions with denominator (x+1)(x−3)(x+3): \(\frac{8}{x^2−2x−3}\), \(\frac{3x}{x^2+4x+3}\).
- Answer
-
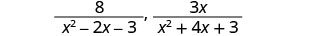
Factor each denominator.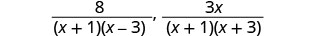 
Find the LCD.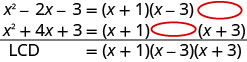 
Multiply each denominator by the 'missing' factor and multiply each numerator by the same factor.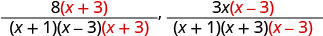 
Simplify the numerators.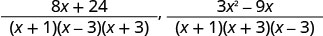 
Rewrite as equivalent rational expressions with denominator (x+3)(x−4)(x+4):
\(\frac{2}{x^2−x−12}\), \(\frac{1}{x^2−16}\).
- Answer
-
\(\frac{2x+8}{(x−4)(x+3)(x+4)}\),
\(\frac{x+3}{(x−4)(x+3)(x+4)}\)
Rewrite as equivalent rational expressions with denominator (x+3)(x+5)(x+6)
\(\frac{x}{x^2+8x+15}\), \(\frac{5}{x^2+9x+18}\).
- Answer
-
\(\frac{x^2+6x}{(x+3)(x+5)(x+6)}\),
\(\frac{x+3}{(x+3)(x+5)(x+6)}\)
Add Rational Expressions with Different Denominators
Now we have all the steps we need to add rational expressions with different denominators. As we have done previously, we will do one example of adding numerical fractions first.
Add: \(\frac{7}{12}+\frac{5}{18}\).
- Answer
-
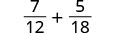
Find the LCD of 12 and 18.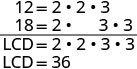 
Rewrite each fraction as an equivalent fraction with the LCD.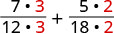 
Add the fractions.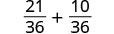 
The fraction cannot be simplified.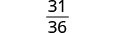 
Add: \(\frac{11}{30}+\frac{7}{12}\).
- Answer
-
\(\frac{19}{20}\)
Add: \(\frac{3}{8}+\frac{9}{20}\).
- Answer
-
\(\frac{33}{40}\)
Now we will add rational expressions whose denominators are monomials.
Add: \(\frac{5}{12x^{2}y}+\frac{4}{21xy^2}\).
- Answer
-
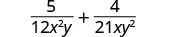
Find the LCD of \(12x^{2}y\) and \(21xy^2\)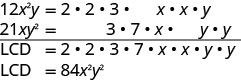
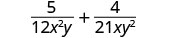
Rewrite each rational expression as an equivalent fraction with the LCD.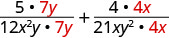 
Simplify.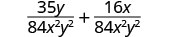 
Add the rational expressions.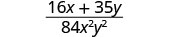 
There are no factors common to the numerator and denominator. The fraction cannot be simplified.
Add: \(\frac{2}{15a^{2}b}+\frac{5}{6ab^2}\).
- Answer
-
\(\frac{4b+25a}{30a^{2}b^2}\)
Add: \(\frac{5}{16c}+\frac{3}{8cd^2}\).
- Answer
-
\(\frac{5d^2+6}{16cd^2}\)
Now we are ready to tackle polynomial denominators.
How to Add Rational Expressions with Different Denominators
Add: \(\frac{3}{x−3}+\frac{2}{x−2}\).
- Answer
-
Add: \(\frac{2}{x−2}+\frac{5}{x+3}\).
- Answer
-
\(\frac{7x−4}{(x+3)(x−2)}\)
Add: \(\frac{4}{m+3}+\frac{3}{m+4}\).
- Answer
-
\(\frac{7m+25}{(m+3)(m+4)}\)
The steps to use to add rational expressions are summarized in the following procedure box.
- Determine if the expressions have a common denominator.
Yes – go to step 2.
No – Rewrite each rational expression with the LCD.
Find the LCD.
Rewrite each rational expression as an equivalent rational expression with the LCD. - Add the rational expressions.
- Simplify, if possible.
Add: \(\frac{2a}{2ab+b^2}+\frac{3a}{4a^2−b^2}\).
- Answer
-
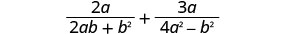
Do the expressions have a common denominator? No.
Rewrite each expression with the LCD.Find the LCD.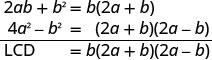 
Rewrite each rational expression as an equivalent rational expression with the LCD.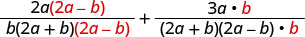 
Simplify the numerators.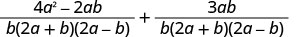 
Add the rational expressions.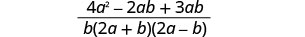 
Simplify the numerator.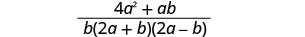 
Factor the numerator.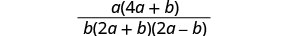 
There are no factors common to the numerator and denominator. The fraction cannot be simplified.
Add: \(\frac{5x}{xy−y^2}+\frac{2x}{x^2+y^2}\).
- Answer
-
\(\frac{x(5x+7y)}{y(x−y)(x+y)}\)
Add: \(\frac{7}{2m+6}+\frac{4}{m^2+4m+3}\).
- Answer
-
\(\frac{7m+15}{2(m+3)(m+1)}\)
Avoid the temptation to simplify too soon! In the example above, we must leave the first rational expression as \(\frac{2a(2a−b)}{b(2a+b)(2a−b)}\) to be able to add it to \(\frac{3a·b}{(2a+b)(2a−b)·b}\).
Add: \(\frac{8}{x^2−2x−3}+\frac{3x}{x^2+4x+3}\).
- Answer
-
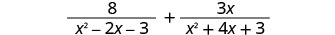
Do the expressions have a common denominator? No.
Rewrite each expression with the LCD.Find the LCD.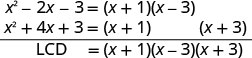 
Rewrite each rational expression as an equivalent fraction with the LCD.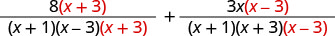 
Simplify the numerators.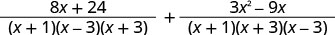 
Add the rational expressions.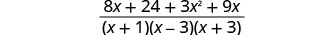 
Simplify the numerator.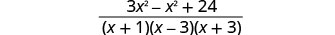 
The numerator is prime, so there are no common factors.
Add: \(\frac{1}{m^2−m−2}+\frac{5m}{m^2+3m+2}\).
- Answer
-
\(\frac{5m^2−9m+2}{(m−2)(m+1)(m+2)}\)
Add: \(\frac{2n}{n^2−3n−10}+\frac{6}{n^2+5n+6}\).
- Answer
-
\(\frac{2(n2+6n−15)}{(n+2)(n−5)(n+3)}\)
Subtract Rational Expressions with Different Denominators
The process we use to subtract rational expressions with different denominators is the same as for addition. We just have to be very careful of the signs when subtracting the numerators.
How to Subtract Rational Expressions with Different Denominators
Subtract: \(\frac{x}{x−3}−\frac{x−2}{x+3}\).
- Answer
-
Subtract: \(\frac{y}{y+4}−\frac{y−2}{y−5}\).
- Answer
-
\(\frac{−7y+8}{(y+4)(y−5)}\)
Subtract: \(\frac{z+3}{z+2}−\frac{z}{z+3}\).
- Answer
-
\(\frac{4z+9}{(z+2)(z+3)}\)
The steps to take to subtract rational expressions are listed below.
- Determine if they have a common denominator.
Yes – go to step 2.
No – Rewrite each rational expression with the LCD.
Find the LCD.
Rewrite each rational expression as an equivalent rational expression with the LCD. - Subtract the rational expressions.
- Simplify, if possible.
Subtract: \(\frac{8y}{y^2−16}−\frac{4}{y−4}\).
- Answer
-
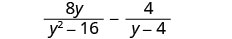
Do the expressions have a common denominator? No.
Rewrite each expression with the LCD.Find the LCD.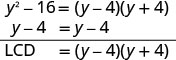 
Rewrite each rational expression as an equivalent rational expression with the LCD.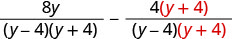 
Simplify the numerators.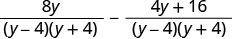 
Subtract the rational expressions.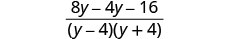 
Simplify the numerators.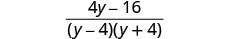 
Factor the numerator to look for common factors. 
Remove common factors.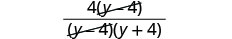 
Simplify. 
Subtract: \(\frac{2x}{x^2−4}−\frac{1}{x+2}\).
- Answer
-
\(\frac{1}{x−2}\)
Subtract: \(\frac{3}{z+3}−\frac{6z}{z^2−9}\).
- Answer
-
\(\frac{−3}{z−3}\)
There are lots of negative signs in the next example. Be extra careful!
Subtract: \(\frac{−3n−9}{n^2+n−6}−\frac{n+3}{2−n}\).
- Answer
-
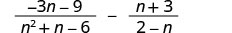
Factor the denominator.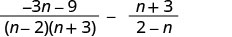 
Since n−2 and 2−n are opposites, we will multiply the second rational expression by \(\frac{−1}{−1}\).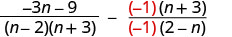 
Simplify.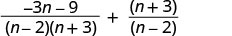 
Do the expressions have a common denominator? No. Find the LCD.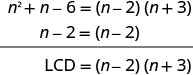 
Rewrite each rational expression as an equivalent rational expression with the LCD.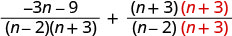 
Simplify the numerators.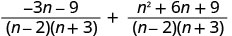 
Simplify the rational expressions.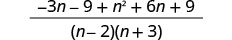 
Simplify the numerator.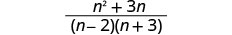 
Factor the numerator to look for common factors.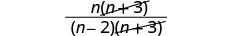 
Simplify.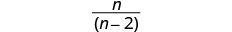 
Subtract: \(\frac{3x−1}{x^2−5x−6}−\frac{2}{6−x}\).
- Answer
-
\(\frac{1}{x−6}\)
Subtract: \(\frac{−2y−2}{y^2+2y−8}−\frac{y−1}{2−y}\).
- Answer
-
\(\frac{y+3}{y+4}\)
When one expression is not in fraction form, we can write it as a fraction with denominator 1.
Subtract: \(\frac{5c+4}{c−2}−3\).
- Answer
-
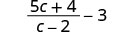
Write 3 as \(\frac{3}{1}\) to have 2 rational expressions.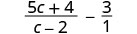 
Do the rational expressions have a common denominator? No. Find the LCD of c−2 and 1. LCD = c−2. Rewrite \(\frac{3}{1}\) as an equivalent rational expression with the LCD.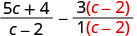 
Simplify.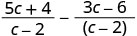 
Subtract the rational expressions.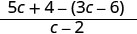 
Simplify.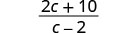 
Factor to check for common factors.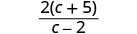 
There are no common factors; the rational expression is simplified.
Subtract: \(\frac{2x+1}{x−7}−3\).
- Answer
-
\(\frac{−x+22}{x−7}\)
Subtract: \(\frac{4y+3}{2y−1}−5\).
- Answer
-
\(\frac{−2(3y−4)}{2y−1}\)
- Determine if the expressions have a common denominator.
Yes – go to step 2.
No – Rewrite each rational expression with the LCD.
Find the LCD.
Rewrite each rational expression as an equivalent rational expression with the LCD. - Add or subtract the rational expressions.
- Simplify, if possible.
We follow the same steps as before to find the LCD when we have more than two rational expressions. In the next example we will start by factoring all three denominators to find their LCD.
Simplify: \(\frac{2u}{u−1}+\frac{1}{u}−\frac{2u−1}{u^2−u}\).
- Answer
-
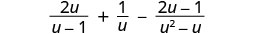
Do the rational expressions have a common denominator? No. Find the LCD.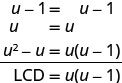 
Rewrite each rational expression as an equivalent rational expression with the LCD.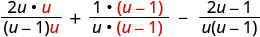 
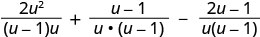
Write as one rational expression.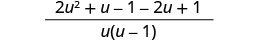 
Simplify.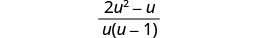 
Factor the numerator, and remove common factors.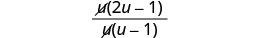 
Simplify.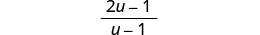 
Simplify: \(\frac{v}{v+1}+\frac{3}{v−1}−\frac{6}{v^2−1}\).
- Answer
-
\(\frac{v+3}{v+1}\)
Add exercises text here.Simplify: \(\frac{3w}{w+2}+\frac{2}{w+7}−\frac{17w+4}{w^2+9w+14}\).
- Answer
-
\(\frac{3w}{w+7}\)
Key Concepts
- Find the Least Common Denominator of Rational Expressions
- Factor each expression completely.
- List the factors of each expression. Match factors vertically when possible.
- Bring down the columns.
- Multiply the factors.
- Add or Subtract Rational Expressions
- Determine if the expressions have a common denominator.
Yes – go to step 2.
No – Rewrite each rational expression with the LCD.- Find the LCD.
- Rewrite each rational expression as an equivalent rational expression with the LCD.
- Add or subtract the rational expressions.
- Simplify, if possible.
- Determine if the expressions have a common denominator.