1.5: Chapter 1 Exercises with Solutions
- Page ID
- 22266
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Exercises \(\PageIndex{1}\) - \(\PageIndex{8}\), find the prime factorization of the given natural number.
80
- Answer
-
\(80=2 \cdot 2 \cdot 2 \cdot 2 \cdot 5\)
108
180
- Answer
-
\(180=2 \cdot 2 \cdot 3 \cdot 3 \cdot 5\)
160
128
- Answer
-
\(128=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\)
192
32
- Answer
-
\(32=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\)
72
In Exercises \(\PageIndex{9}\)-\(\PageIndex{16}\), convert the given decimal to a fraction.
0.648
- Answer
-
There are three decimal places, so \(0.648=\frac{648}{1000}=\frac{81}{125}\)
0.62
0.240
- Answer
-
There are three decimal places, so \(0.240=\frac{240}{1000}=\frac{6}{25}\)
0.90
0.14
- Answer
-
There are two decimal places, so \(0.14=\frac{14}{100}=\frac{7}{50}\)
0.760
0.888
- Answer
-
There are three decimal places, so \(0.888=\frac{888}{1000}=\frac{111}{125}\)
0.104
In Exercises \(\PageIndex{17}\)-\(\PageIndex{24}\), convert the given repeating decimal to a fraction.
\(0 . \overline{27}\)
- Answer
-
Let \(x=0 . \overline{27} .\) Then \(100 x=27 . \overline{27} .\) Subtracting on both sides of these equations.
\[\begin{aligned} 100 x &=27 . \overline{27} \\ x &=0 . \overline{27} \end{aligned} \nonumber \]
yields \(99 x=27 .\) Finally, solve for \(x\) by dividing by \(99 : x=\frac{27}{99}=\frac{3}{11}\).
\(0 . \overline{171}\)
\(0 . \overline{24}\)
- Answer
-
Let \(x=0 . \overline{24} .\) Then \(100 x=24 . \overline{24} .\) Subtracting on both sides of these equations \[\begin{aligned} 100 x &=24 . \overline{24} \\ x &=0 . \overline{24} \end{aligned} \nonumber \]
yields \(99 x=24 .\) Finally, solve for \(x\) by dividing by \(99 : x=\frac{24}{99}=\frac{8}{33}\)
\(0 . \overline{882}\)
\(0 . \overline{84}\)
- Answer
-
Let \(x=0 . \overline{84} .\) Then \(100 x=84 . \overline{84} .\) Subtracting on both sides of these equations
\[\begin{aligned} 100 x &=84 . \overline{.84} \\ x &=0 . \overline{84} \end{aligned} \nonumber \]
yields \(99 x=84 .\) Finally, solve for \(x\) by dividing by \(99 : x=\frac{84}{99}=\frac{28}{33}\)
\(0 . \overline{384}\)
\(0 . \overline{63}\)
- Answer
-
Let \(x=0 . \overline{63} .\) Then \(100 x=63 . \overline{63} .\) Subtracting on both sides of these equations
\[\begin{aligned} 100 x &=63 . \overline{63} \\ x &=0 . \overline{63} \end{aligned} \nonumber \]
yields \(99 x=63 .\) Finally, solve for \(x\) by dividing by \(99 : x=\frac{63}{99}=\frac{7}{11}\)
\(0 . \overline{60}\)
Prove that \(\sqrt{3}\) is irrational.
- Answer
-
Suppose that \(\sqrt{3}\) is rational. Then it can be expressed as the ratio of two integers p and q as follows:
\[\sqrt{3}=\frac{p}{q} \nonumber \]
Square both sides, \[3=\frac{p^{2}}{q^{2}} \nonumber \]
then clear the equation of fractions by multiplying both sides by \(q^{2}\):
\[p^{2}=3 q^{2} \nonumber \]
Now p and q each have their own unique prime factorizations. Both \(p^{2}\) and \(q^{2}\) have an even number of factors in their prime factorizations. But this contradicts equation (1), because the left side would have an even number of factors in its prime factorization, while the right side would have an odd number of factors in its prime factorization (there’s one extra 3 on the right side).
Therefore, our assumption that \(\sqrt{3}\) was rational is false. Thus, \(\sqrt{3}\) is irrational.
Prove that \(\sqrt{5}\) is irrational.
In Exercises \(\PageIndex{27}\)-\(\PageIndex{30}\), copy the given table onto your homework paper. In each row, place a check mark in each column that is appropriate. That is, if the number at the start of the row is rational, place a check mark in the rational column. Note: Most (but not all) rows will have more than one check mark.
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| 0 | |||||
| -2 | |||||
| -2/3 | |||||
| 0.15 | |||||
| \(0 . \overline{2}\) | |||||
| \(\sqrt{5}\) |
- Answer
-
\(\mathbb{N}\) \(\mathbb{W}\) \(\mathbb{Z}\) \(\mathbb{Q}\) \(\mathbb{R}\) 0 x x x x -2 x x x -2/3 x x 0.15 x x \(0 . \overline{2}\) x x \(\sqrt{5}\) x
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| 10/2 | |||||
| \(\pi\) | |||||
| -6 | |||||
| \(0 . \overline{9}\) | |||||
| \(\sqrt{2}\) | |||||
| 0.37 |
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| -4/3 | |||||
| 12 | |||||
| 0 | |||||
| \(\sqrt{11}\) | |||||
| \(1. \overline{3}\) | |||||
| 6/2 |
- Answer
-
\(\mathbb{N}\) \(\mathbb{W}\) \(\mathbb{Z}\) \(\mathbb{Q}\) \(\mathbb{R}\) -4/3 x x 12 x x x x x 0 x x x x \(\sqrt{11}\) x \(1. \overline{3}\) x x 6/2 x x x x x
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| -3/5 | |||||
| \(\sqrt{10}\) | |||||
| 1.625 | |||||
| 10/2 | |||||
| 0/5 | |||||
| 11 |
In Exercises \(\PageIndex{31}\)-\(\PageIndex{42}\), consider the given statement and determine whether it is true or false. Write a sentence explaining your answer. In particular, if the statement is false, try to give an example that contradicts the statement.
All natural numbers are whole numbers.
- Answer
-
True. The only difference between the two sets is that the set of whole numbers contains the number 0.
All whole numbers are rational numbers.
All rational numbers are integers.
- Answer
-
False. For example, \(\frac{1}{2}\) is not an integer.
All rational numbers are whole numbers.
Some natural numbers are irrational.
- Answer
-
False. All natural numbers are rational, and therefore not irrational.
Some whole numbers are irrational.
Some real numbers are irrational.
- Answer
-
True. For example, π and √2 are real numbers which are irrational.
All integers are real numbers.
All integers are rational numbers.
- Answer
-
True. Every integer b can be written as a fraction b/1.
No rational numbers are natural numbers.
No real numbers are integers.
- Answer
-
False. For example, 2 is a real number that is also an integer.
All whole numbers are natural numbers.
In Exercises \(\PageIndex{43}\)-\(\PageIndex{54}\), solve each of the given equations for x.
45x + 12 = 0
- Answer
-
\[\begin{aligned} & 45 x+12=0 \\ \Longrightarrow \quad & 45 x=-12 \\ \Longrightarrow \quad& x=-\frac{12}{45}=-\frac{4}{15} \end{aligned} \nonumber \]
76x − 55 = 0
x − 7 = −6x + 4
- Answer
-
\[\begin{aligned} & x-7=-6 x+4 \\ \Longrightarrow \quad & x+6 x=4+7 \\ \Longrightarrow \quad & 7 x=11 \\ \Longrightarrow \quad & x=\frac{11}{7} \end{aligned} \nonumber \]
−26x + 84 = 48
37x + 39 = 0
- Answer
-
\[\begin{aligned} & 37 x+39=0 \\ \Longrightarrow\quad & 37 x=-39 \\ \Longrightarrow\quad & x=-\frac{39}{37} \end{aligned} \nonumber \]
−48x + 95 = 0
74x − 6 = 91
- Answer
-
\[\begin{aligned} & 74 x-6=91 \\ \Longrightarrow\quad & 74 x=97 \\ \Longrightarrow\quad & x=\frac{97}{74} \end{aligned} \nonumber \]
−7x + 4 = −6
−88x + 13 = −21
- Answer
-
\[\begin{aligned} &-88 x+13=-21 \\ \Longrightarrow\quad &-88 x=-34 \\ \Longrightarrow \quad & x=\frac{-34}{-88}=\frac{17}{44} \end{aligned} \nonumber \]
−14x − 81 = 0
19x + 35 = 10
- Answer
-
\[\begin{aligned} & 19 x+35=10 \\ \Longrightarrow\quad & 19 x=-25 \\ \Longrightarrow\quad & x=-\frac{25}{19} \end{aligned} \nonumber \]
−2x + 3 = −5x − 2
In Exercises \(\PageIndex{55}\)-\(\PageIndex{66}\), solve each of the given equations for x.
6 − 3(x + 1) = −4(x + 6) + 2
- Answer
-
\[\begin{aligned} & 6-3(x+1)=-4(x+6)+2 \\ \Longrightarrow\quad & 6-3 x-3=-4 x-24+2 \\ \Longrightarrow\quad &-3 x+3=-4 x-22 \\ \Longrightarrow\quad &-3 x+4 x=-22-3 \\ \Longrightarrow\quad & x=-25 \end{aligned} \nonumber \]
(8x + 3) − (2x + 6) = −5x + 8
−7 − (5x − 3) = 4(7x + 2)
\[\begin{aligned} &-7-(5 x-3)=4(7 x+2) \\ \Longrightarrow\quad &-7-5 x+3=28 x+8 \\ \Longrightarrow\quad &-5 x-4=28 x+8 \\ \Longrightarrow\quad &-5 x-28 x=8+4 \\ \Longrightarrow\quad &-33 x=12 \\ \Longrightarrow\quad & x=-\frac{12}{33}=-\frac{4}{11} \end{aligned} \nonumber \]
−3 − 4(x + 1) = 2(x + 4) + 8
9 − (6x − 8) = −8(6x − 8)
- Answer
-
\[\begin{aligned} & 9-(6 x-8)=-8(6 x-8) \\ \Longrightarrow \quad & 9-6 x+8=-48 x+64 \\ \Longrightarrow\quad &-6 x+17=-48 x+64 \\ \Longrightarrow\quad &-6 x+48 x=64-17 \\ \Longrightarrow\quad & 42 x=47 \\ \Longrightarrow\quad & x=\frac{47}{42} \end{aligned} \nonumber \]
−9 − (7x − 9) = −2(−3x + 1)
(3x − 1) − (7x − 9) = −2x − 6
- Answer
-
\[\begin{aligned} &(3 x-1)-(7 x-9)=-2 x-6 \\ \Longrightarrow\quad & 3 x-1-7 x+9=-2 x-6 \\ \Longrightarrow\quad &-4 x+8=-2 x-6 \\ \Longrightarrow\quad &-4 x+2 x=-6-8 \\ \Longrightarrow\quad &-2 x=-14 \\ \Longrightarrow\quad & x=7 \end{aligned} \nonumber \]
−8 − 8(x − 3) = 5(x + 9) + 7
(7x − 9) − (9x + 4) = −3x + 2
- Answer
-
\[\begin{aligned} &(7 x-9)-(9 x+4)=-3 x+2 \\ \Longrightarrow\quad & 7 x-9-9 x-4=-3 x+2 \\ \Longrightarrow\quad &-2 x-13=-3 x+2 \\ \Longrightarrow\quad &-2 x+3 x=2+13 \\ \Longrightarrow\quad & x=15 \end{aligned} \nonumber \]
(−4x − 6) + (−9x + 5) = 0
−5 − (9x + 4) = 8(−7x − 7)
- Answer
-
\[\begin{array}{ll}{} & {-5-(9 x+4)=8(-7 x-7)} \\ {\Longrightarrow} & {-5-9 x-4=-56 x-56} \\ {\Longrightarrow} & {-9 x-9=-56 x-56} \\ {\Longrightarrow} & {-9 x+56 x=-56+9} \\ {\Longrightarrow} & {47 x=-47} \\ {\Longrightarrow} & {x=-1}\end{array} \nonumber \]
(8x − 3) + (−3x + 9) = −4x − 7
In Exercises \(\PageIndex{67}\)-\(\PageIndex{78}\), solve each of the given equations for x. Check your solutions using your calculator.
−3.7x − 1 = 8.2x − 5
- Answer
-
First clear decimals by multiplying by 10.
\[\begin{aligned} &-3.7 x-1=8.2 x-5 \\ \Longrightarrow\quad &-37 x-10=82 x-50 \\ \Longrightarrow\quad &-37 x-82 x=-50+10 \\ \Longrightarrow\quad &-119 x=-40 \\ \Longrightarrow\quad & x=\frac{40}{119} \end{aligned} \nonumber \]
Here is a check of the solutions on the graphing calculator. The left-hand side of the equation is evaluated at the solution in (a), the right-hand side of the equation is evaluated at the solution in (b). Note that they match.

8.48x − 2.6 = −7.17x − 7.1
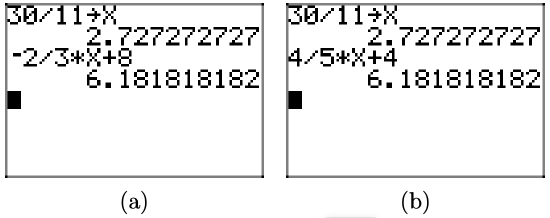
\(-\frac{2}{3} x+8=\frac{4}{5} x+4\)
- Answer
-
First clear fractions by multiplying by 15.
\[\begin{aligned} &-\frac{2}{3} x+8=\frac{4}{5} x+4 \\ \Longrightarrow\quad &-10 x+120=12 x+60 \\ \Longrightarrow\quad &-10 x-12 x=60-120 \\ \Longrightarrow\quad &-22 x=-60 \\ \Longrightarrow\quad & x=\frac{-60}{-22}=\frac{30}{11} \end{aligned} \nonumber \]
Here is a check of the solutions on the graphing calculator. The left-hand side of the equation is evaluated at the solution in (a), the right-hand side of the equation is evaluated at the solution in (b). Note that they match.
−8.4x = −4.8x + 2
\(-\frac{3}{2} x+9=\frac{1}{4} x+7\)
- Answer
-
First clear fractions by multiplying by 4.
\[\begin{aligned} &-\frac{3}{2} x+9=\frac{1}{4} x+7 \\ \Longrightarrow\quad &-6 x+36=x+28 \\ \Longrightarrow\quad &-6 x-x=28-36 \\ \Longrightarrow\quad &-7 x=-8 \\ \Longrightarrow\quad & x=\frac{8}{7} \end{aligned} \nonumber \]
Here is a check of the solutions on the graphing calculator. The left-hand side of the equation is evaluated at the solution in (a), the right-hand side of the equation is evaluated at the solution in (b). Note that they match.

2.9x − 4 = 0.3x − 8
5.45x + 4.4 = 1.12x + 1.6
- Answer
-
First clear decimals by multiplying by 100.
\[\begin{aligned} & 5.45 x+4.4=1.12 x+1.6 \\ \Longrightarrow\quad & 545 x+440=112 x+160 \\ \Longrightarrow\quad & 545 x-112 x=160-440 \\ \Longrightarrow\quad & 433 x=-280 \\ \Longrightarrow\quad & x=-\frac{280}{433} \end{aligned} \nonumber \]
Here is a check of the solutions on the graphing calculator. The left-hand side of the equation is evaluated at the solution in (a), the right-hand side of the equation is evaluated at the solution in (b). Note that they match.

\(-\frac{1}{4} x+5=-\frac{4}{5} x-4\)
\(-\frac{3}{2} x-8=\frac{2}{5} x-2\)
- Answer
-
First clear fractions by multiplying by 10. \[\begin{aligned} &-\frac{3}{2} x-8=\frac{2}{5} x-2 \\ \Longrightarrow\quad &-15 x-80=4 x-20 \\ \Longrightarrow\quad &-15 x-4 x=-20+80 \\ \Longrightarrow\quad &-19 x=60 \\ \Longrightarrow\quad & x=-\frac{60}{19} \end{aligned} \nonumber \]
Here is a check of the solutions on the graphing calculator. The left-hand side of the equation is evaluated at the solution in (a), the right-hand side of the equation is evaluated at the solution in (b). Note that they match.

\(-\frac{4}{3} x-8=-\frac{1}{4} x+5\)
−4.34x − 5.3 = 5.45x − 8.1
- Answer
-
First clear decimals by multiplying by 100.
\[\begin{aligned} &-4.34 x-5.3=5.45 x-8.1 \\ \Longrightarrow\quad &-434 x-530=545 x-810 \\ \Longrightarrow\quad &-434 x-545 x=-810+530 \\ \Longrightarrow\quad &-979 x=-280 \\ \Longrightarrow\quad & x=\frac{280}{979} \end{aligned} \nonumber \]
Here is a check of the solutions on the graphing calculator. The left-hand side of the equation is evaluated at the solution in (a), the right-hand side of the equation is evaluated at the solution in (b). Note that they match.

\(\frac{2}{3} x-3=-\frac{1}{4} x-1\)
In Exercises \(\PageIndex{79}\)-50, solve each of the given equations for the indicated variable.
P = IRT for R
- Answer
-
\[\begin{aligned} & P=I R T \\ \Longrightarrow\quad & P=(I T) R \\ \Longrightarrow\quad & \frac{P}{I T}=\frac{(I T) R}{I T} \\ \Longrightarrow\quad & \frac{P}{I T}=R \end{aligned} \nonumber \]
d = vt for t
\(v=v_{0}+a t\) for \(a\)
- Answer
-
\[\begin{aligned} & v=v_{0}+a t \\ \Longrightarrow\quad & v-v_{0}=a t \\ \Longrightarrow\quad & \frac{v-v_{0}}{t}=a \end{aligned} \nonumber \]
\(x=v_{0}+v t\) for \(v\)
Ax + By = C for y
- Answer
-
\[\begin{aligned} & A x+B y=C \\ \Longrightarrow\quad & B y=C-A x \\ \Longrightarrow\quad & y=\frac{C-A x}{B} \end{aligned} \nonumber \]
y = mx + b for x
\(A=\pi r^{2}\) for \(\pi\)
- Answer
-
\[\begin{aligned} A &=\pi r^{2} \\ \Longrightarrow \quad \frac{A}{r^{2}} &=\pi \end{aligned} \nonumber \]
\(S=2 \pi r^{2}+2 \pi r h\) for \(h\)
\(F=\frac{k q q_{0}}{r^{2}}\) for \(k\)
- Answer
-
\[\begin{aligned} & F=\frac{k q q_{0}}{r^{2}} \\ \Longrightarrow\quad & F r^{2}=k q q_{0} \\ \Longrightarrow\quad & \frac{F r^{2}}{q q_{0}}=k \end{aligned} \nonumber \]
\(C=\frac{Q}{m T}\) for \(T\)
\(\frac{V}{t}=k\) for \(t\)
- Answer
-
\[\begin{aligned} & \frac{V}{t}=k \\ \Longrightarrow\quad & V=k t \\ \Longrightarrow\quad & \frac{V}{k}=t \end{aligned} \nonumber \]
\(\lambda=\frac{h}{m v}\) for \(v\)
\(\frac{P_{1} V_{1}}{n_{1} T_{1}}=\frac{P_{2} V_{2}}{n_{2} T_{2}}\) for \(V_{2}\)
- Answer
-
Cross multiply, then divide by the coefficient of \(V_{2}\).
\[\begin{aligned} & \frac{P_{1} V_{1}}{n_{1} T_{1}}=\frac{P_{2} V_{2}}{n_{2} T_{2}} \\ \Longrightarrow\quad & n_{2} P_{1} V_{1} T_{2}=n_{1} P_{2} V_{2} T_{1} \\ \Longrightarrow\quad & \frac{n_{2} P_{1} V_{1} T_{2}}{n_{1} P_{2} T_{1}}=V_{2} \end{aligned} \nonumber \]
\(\pi=\frac{n R T}{V} i\) for \(n\)
Tie a ball to a string and whirl it around in a circle with constant speed. It is known that the acceleration of the ball is directly toward the center of the circle and given by the formula \[a=\frac{v^{2}}{r} \nonumber \] where a is acceleration, v is the speed of the ball, and r is the radius of the circle of motion.
i. Solve formula (1) for r.
ii. Given that the acceleration of the ball is 12 m/s2 and the speed is 8 m/s, find the radius of the circle of motion.
- Answer
-
Cross multiply, then divide by the coefficient of r.
\[\begin{aligned} a &=\frac{v^{2}}{r} \\ a r &=v^{2} \\ r &=\frac{v^{2}}{a} \end{aligned} \nonumber \]
To find the radius, substitute the acceleration \(a=12 \mathrm{m} / \mathrm{s}^{2}\) and speed v = 8 m/s.
\[r=\frac{v^{2}}{a}=\frac{(8)^{2}}{12}=\frac{64}{12}=\frac{16}{3} \nonumber \]
Hence, the radius is \(r=16 / 3 \mathrm{m},\) or 5\(\frac{1}{3}\) meters.
A particle moves along a line with constant acceleration. It is known the velocity of the particle, as a function of the amount of time that has passed, is given by the equation
\[v=v_{0}+a t \nonumber \] where v is the velocity at time t, v0 is the initial velocity of the particle (at time t = 0), and a is the acceleration of the particle.
i. Solve formula (2) for t.
ii. You know that the current velocity of the particle is 120 m/s. You also know that the initial velocity was 40 m/s and the acceleration has been a constant \(a=2 \mathrm{m} / \mathrm{s}^{2}\). How long did it take the particle to reach its current velocity?
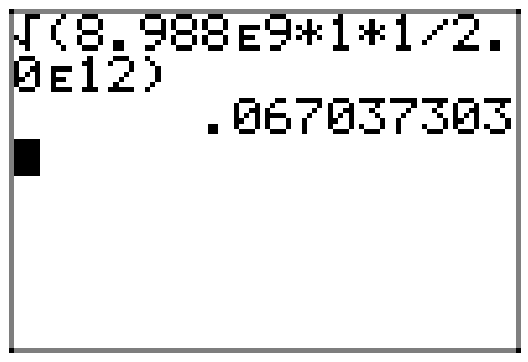
Like Newton’s Universal Law of Gravitation, the force of attraction (repulsion) between two unlike (like) charged particles is proportional to the product of the charges and inversely proportional to the distance between them. \[F=k_{C} \frac{q_{1} q_{2}}{r^{2}} \nonumber \] In this formula, \(k_{C} \approx 8.988 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\) and is called the electrostatic constant. The variables q1 and q2 represent the charges (in Coulombs) on the particles (which could either be positive or negative numbers) and r represents the distance (in meters) between the charges. Finally, F represents the force of the charge, measured in Newtons.
i. Solve formula (3) for r.
ii. Given a force \(F=2.0 \times 10^{12} \mathrm{N}\), two equal charges \(q_{1}=q_{2}=1 \mathrm{C}\), find the approximate distance between the two charged particles.
- Answer
-
Cross multiply, then divide by the coefficient of r.
\[\begin{aligned} F &=k_{C} \frac{q_{1} q_{2}}{r^{2}} \\ F r^{2} &=k_{C} q_{1} q_{2} \\ r^{2} &=\frac{k_{C} q_{1} q_{2}}{F} \end{aligned} \nonumber \]
Finally, to find r, take the square root.
\[r=\sqrt{\frac{k_{C} q_{1} q_{2}}{F}} \nonumber \]
To find the distance between the charged particles, substitute \(k_{C}=8.988 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\),
\(q_{1}=q_{2}=1 \mathrm{C},\) and \(F=2.0 \times 10^{12} \mathrm{N}\).\[r=\sqrt{\frac{\left(8.988 \times 10^{9}\right)(1)(1)}{2.0 \times 10^{12}}} \nonumber \]
A calculator produces an approximation, \(r \approx 0.067\) meters.
Perform each of the following tasks in Exercises \(\PageIndex{96}\)-\(\PageIndex{99}\).
i. Write out in words the meaning of the symbols which are written in set-builder notation.
ii. Write some of the elements of this set.
iii. Draw a real line and plot some of the points that are in this set.
\(A=\{x \in \mathbb{N} : x>10\}\)
- Answer
-
i. A is the set of all \(x\) in the natural numbers such that \(x\) is greater than \(10.\)
ii. \(A=\{11,12,13,14, \ldots\}\)
iii.

\(B=\{x \in \mathbb{N} : x \geq 10\}\)
\(C=\{x \in \mathbb{Z} : x \leq 2\}\)
- Answer
-
i. C is the set of all \(x\) in the integers such that \(x\) is less than or equal to \(2.\)
ii. \(C=\{\ldots,-4,-3,-2,-1,0,1,2\}\)
iii.

\(D=\{x \in \mathbb{Z} : x>-3\}\)
In Exercises \(\PageIndex{100}\)-\(\PageIndex{103}\), use the sets A, B, C, and D that were defined in Exercises \(\PageIndex{96}\)-\(\PageIndex{99}\). Describe the following sets using set notation, and draw the corresponding Venn Diagram.
\(A \cap B\)
- Answer
-
\(A \cap B=\{x \in \mathbb{N} : x>10\}=\{11,12,13, \ldots\}\)
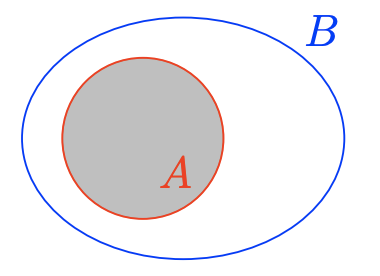
\(A \cup B\)
\(A \cup C\)
- Answer
-
\(A \cup C=\{x \in \mathbb{Z} : x \leq 2 \text { or } x>10\}=\{\ldots,-3,-2-1,0,1,2,11,12,13 \dots\}\)
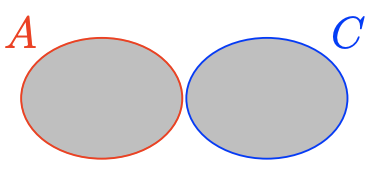
\(C \cap D\)
In Exercises \(\PageIndex{104}\)-\(\PageIndex{111}\), use both interval and set notation to describe the interval shown on the graph.

- Answer
-
The filled circle at the endpoint 3 indicates this point is included in the set. Thus, the set in interval notation is \([3, \infty)\), and in set notation \(\{x : x \geq 3\}\).


- Answer
-
The empty circle at the endpoint −7 indicates this point is not included in the set. Thus, the set in interval notation is \((-\infty,-7)\), and in set notation is \(\{x : x<-7\}\).


- Answer
-
The empty circle at the endpoint 0 indicates this point is not included in the set. Thus, the set in interval notation is \((0, \infty)\), and in set notation is \(\{x : x>0\}\).


- Answer
-
The empty circle at the endpoint −8 indicates this point is not included in the set. Thus, the set in interval notation is \((-8, \infty)\), and in set notation is \(\{x : x>-8\}\).

In Exercises \(\PageIndex{112}\)-\(\PageIndex{119}\), sketch the graph of the given interval.
\([2,5)\)
- Answer
-

\((-3,1]\)
\([1, \infty)\)
- Answer
-

\((-\infty, 2)\)
\(\{x :-4<x<1\}\)
- Answer
-

\(\{x : 1 \leq x \leq 5\}\)
\(\{x : x<-2\}\)
- Answer
-

\(\{x : x \geq-1\}\)
In Exercises \(\PageIndex{120}\)-\(\PageIndex{127}\), use both interval and set notation to describe the intersection of the two intervals shown on the graph. Also, sketch the graph of the intersection on the real number line.
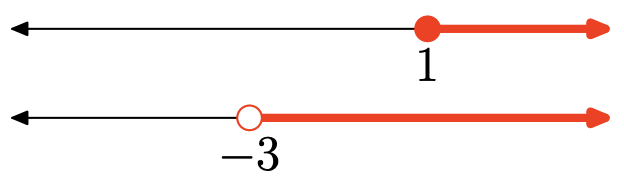
- Answer
-
The intersection is the set of points that are in both intervals (shaded on both graphs). Graph of the intersection:

\([1, \infty)=\{x : x \geq 1\}\)
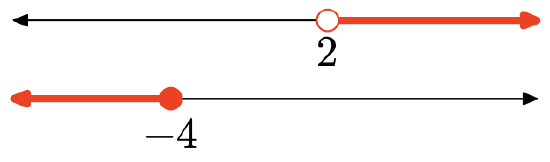
- Answer
-
There are no points that are in both intervals (shaded in both), so there is no intersection. Graph of the intersection:

no intersection
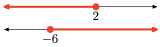
- Answer
-
The intersection is the set of points that are in both intervals (shaded in both). Graph of the intersection:

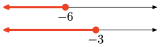
\([-6,2]=\{x :-6 \leq x \leq 2\}\)

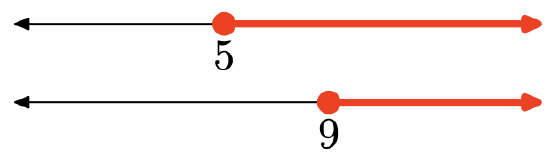
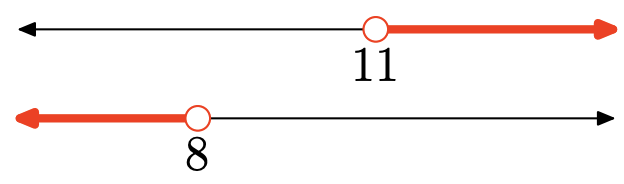
- Answer
-
The intersection is the set of points that are in both intervals (shaded in both). Graph of the intersection:

\([9, \infty)=\{x : x \geq 9\}\)
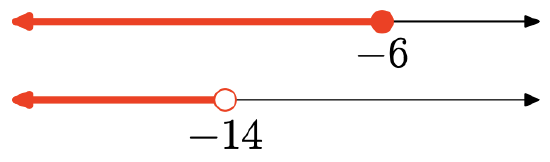
In Exercises \(\PageIndex{128}\)-\(\PageIndex{135}\), use both interval and set notation to describe the union of the two intervals shown on the graph. Also, sketch the graph of the union on the real number line.
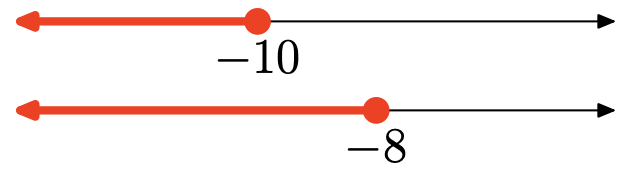
- Answer
-
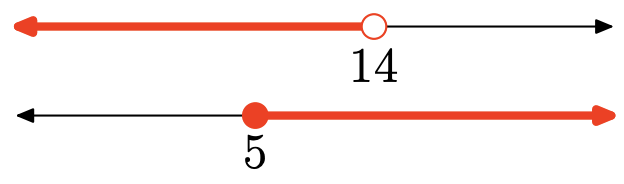
The union is the set of all points that are in one interval or the other (shaded in either graph). Graph of the union:

\((-\infty,-8]=\{x : x \leq-8\}\)

- Answer
-
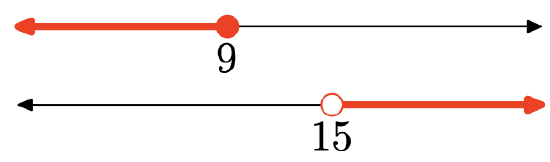
The union is the set of all points that are in one interval or the other (shaded in either graph). Graph of the union:

\((-\infty, 9] \cup(15, \infty)\)
\(=\{x : x \leq 9 \text { or } x>15\}\)
- Answer
-
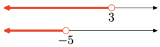
The union is the set of all points that are in one interval or the other (shaded in either). Graph of the union:

\((-\infty, 3)=\{x : x<3\}\)
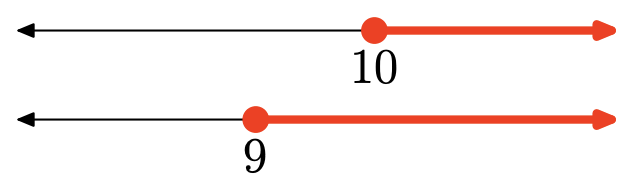
- Answer
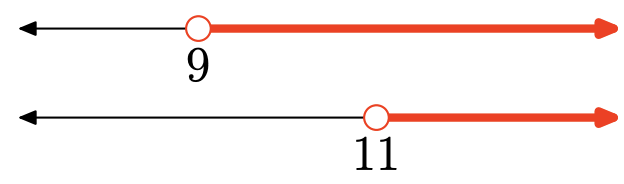
-
The union is the set of all points that are in one interval or the other (shaded in either). Graph of the union:

\([9, \infty)=\{x : x \geq 9\}\)

In Exercises \(\PageIndex{136}\)-56, use interval notation to describe the given set. Also, sketch the graph of the set on the real number line.
\(\{x : x \geq-6 \text { and } x>-5\}\)
- Answer
-
This set is the same as \(\{x : x>-5\}\), which is \((-5, \infty)\) in interval notation. Graph of the set:

\(\{x : x \leq 6 \text { and } x \geq 4\}\)
\(\{x : x \geq-1 \text { or } x<3\}\)
- Answer
-
Every real number is in one or the other of the two intervals. Therefore, the set is the set of all real numbers \((-\infty, \infty)\). Graph of the set:

\(\{x : x>-7 \text { and } x>-4\}\)
\(\{x : x \geq -1 \text { or } x>6\}\)
- Answer
-
This set is the same as \(\{x : x \geq-1\}\), which is \([-1, \infty)\) in interval notation. Graph of the set:

\(\{x : x \geq 7 \text { or } x<-2\}\)
\(\{x : x \geq 6 \text { or } x>-3\}\)
- Answer
-
This set is the same as \(\{x : x>-3\}\), which is \((-3, \infty)\) in interval notation. Graph of the set:

\(\{x : x \leq 1 \text { or } x>0\}\)
\(\{x : x<2 \text { and } x<-7\}\)
- Answer
-
This set is the same as \(\{x : x<-7\}\), which is \((-\infty,-7)\) in interval notation. Graph of the set:

\(\{x : x \leq-3 \text { and } x<-5\}\)
\(\{x : x \leq-3 \text { or } x \geq 4\}\)
- Answer
-
This set is the union of two intervals, \((-\infty,-3] \cup[4, \infty)\). Graph of the set:

\(\{x : x<11 \text { or } x \leq 8\}\)
\(\{x : x \geq 5 \text { and } x \leq 1\}\)
- Answer
-
There are no numbers that satisfy both inequalities. Thus, there is no intersection. Graph of the set:

\(\{x : x<5 \text { or } x<10\}\)
\(\{x : x \leq 5 \text { and } x \geq-1\}\)
- Answer
-
This set is the same as \(\{x :-1 \leq x \leq 5\}\), which is [−1, 5] in interval notation. Graph of the set

\(\{x : x>-3 \text { and } x<-6\}\)
In Exercises \(\PageIndex{152}\)-\(\PageIndex{163}\), solve the inequality. Express your answer in both interval and set notations, and shade the solution on a number line.
\(-8 x-3 \leq-16 x-1\)
- Answer
-
\[\begin{aligned} & -8 x-3 \leq-16 x-1 \\ \Longrightarrow \quad & − 8x + 16x \leq −1 + 3 \\ \Longrightarrow \quad& 8x \leq 2 \\ \Longrightarrow \quad & x \leq \frac{1}{4}\end{aligned} \nonumber \]
Thus, the solution interval is \((−\infty, \frac{1}{4}]\) = \(\{x|x \leq \frac{1}{4}\}\).

\(6 x-6>3 x+3\)
\(-12 x+5 \leq-3 x-4\)
- Answer
-
\[\begin{aligned} & -12 x+5 \leq-3 x-4 \\ \Longrightarrow \quad & -12x + 3x \leq −4 − 5 \\ \Longrightarrow \quad& -9x \leq -9 \\ \Longrightarrow \quad & x \geq 1\end{aligned} \nonumber \]
Thus, the solution interval is \([1,\infty) = \{x|x \geq 1\}\).

\(7 x+3 \leq-2 x-8\)
\(-11 x-9<-3 x+1\)
- Answer
-
\[\begin{aligned} & − 11x − 9 < −3x + 1 \\ \Longrightarrow \quad & − 11x + 3x < 1 + 9 \\ \Longrightarrow \quad& − 8x < 10 \\ \Longrightarrow \quad & x > -\frac{5}{4}\end{aligned} \nonumber \]
Thus, the solution interval is \((−\frac{5}{4} ,\infty) = \{x|x >−\frac{5}{4} \}\).

\(4 x-8 \geq-4 x-5\)
\(4 x-5>5 x-7\)
- Answer
-
\[\begin{aligned} & 4x − 5 > 5x − 7\\ \Longrightarrow \quad & 4x − 5x > −7 + 5 \\ \Longrightarrow \quad& − x > −2 \\ \Longrightarrow \quad &x < 2\end{aligned} \nonumber \]
Thus, the solution interval is \((−\infty, 2) = \{x|x < 2\}\).
\(-14 x+4>-6 x+8\)
\(2 x-1>7 x+2\)
- Answer
-
\[\begin{aligned} & 2x − 1 > 7x + 2\\ \Longrightarrow \quad & 2x − 7x > 2 + 1 \\ \Longrightarrow \quad& − 5x > 3 \\ \Longrightarrow \quad &x < −\frac{3}{5}\end{aligned} \nonumber \]
Thus, the solution interval is \((−\infty, −\frac{3}{5}) = \{x|x < −\frac{3}{5}\}\).
\(-3 x-2>-4 x-9\)
\(-3 x+3<-11 x-3\)
- Answer
-
\[\begin{aligned} & − 3x + 3 < −11x − 3\\ \Longrightarrow \quad & − 3x + 11x < −3 − 3 \\ \Longrightarrow \quad& 8x < −6 \\ \Longrightarrow \quad &x < -\frac{3}{4}\end{aligned} \nonumber \]
Thus, the solution interval is \((−\infty, −\frac{3}{4}) = \{x|x < −\frac{3}{4}\}\).
\(6 x+3<8 x+8\)
In Exercises 13-50, solve the compound inequality. Express your answer in both interval and set notations, and shade the solution on a number line.
\(2 x-1<4\) or \(7 x+1 \geq-4\)
- Answer
-
\[\begin{aligned} & 2x − 1 < 4 \text{ or } 7x + 1 \geq −4\\ \Longrightarrow \quad & 2x < 5\quad \text{or}\quad 7x \geq −5 \\ \Longrightarrow \quad&x<\frac{5}{2}\quad\text{or}\quad x\geq-\frac{5}{7}\end{aligned} \nonumber \]

For the union, shade anything shaded in either graph. The solution is the set of all real numbers \((−\infty,\infty)\).

\(-8 x+9<-3\) and \(-7 x+1>3\)
\(-6 x-4<-4\) and \(-3 x+7 \geq-5\)
- Answer
-
\[\begin{aligned} & − 6x − 4 < −4 \text{ and } − 3x + 7 \geq −5\\ \Longrightarrow \quad & -6x < 0\quad \text{and}\quad -3x \geq −12 \\ \Longrightarrow \quad&x>0\quad\text{and}\quad x\leq4 \\ \Longrightarrow \quad & 0< x \leq 4 \end{aligned} \nonumber \]
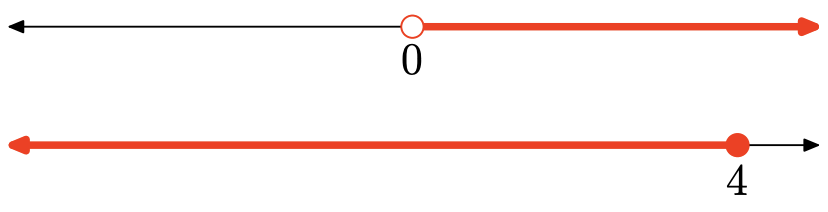
The intersection is all points shaded in both graphs, so the solution is \((0, 4] = \{x|0 < x \leq 4\}\).

\(-3 x+3 \leq 8\) and \(-3 x-6>-6\)
\(8 x+5 \leq-1\) and \(4 x-2>-1\)
- Answer
-
Add texts here. Do not delete this text first.
\(-x-1<7\) and \(-6 x-9 \geq 8\)
\(-3 x+8 \leq-5\) or \(-2 x-4 \geq-3\)
- Answer
-
Add texts here. Do not delete this text first.
\(-6 x-7<-3\) and \(-8 x \geq 3\)
\(9 x-9 \leq 9\) and \(5 x>-1\)
- Answer
-
Add texts here. Do not delete this text first.
\(-7 x+3<-3\) or \(-8 x \geq 2\)
- Answer
-
Add texts here. Do not delete this text first.
\(3 x-5<4\) and \(-x+9>3\)
- Answer
-
Add texts here. Do not delete this text first.
\(-8 x-6<5\) or \(4 x-1 \geq 3\)
- Answer
-
Add texts here. Do not delete this text first.
\(9 x+3 \leq-5\) or \(-2 x-4 \geq 9\)
- Answer
-
Add texts here. Do not delete this text first.
\(-7 x+6<-4\) or \(-7 x-5>7\)
- Answer
-
Add texts here. Do not delete this text first.
\(4 x-2 \leq 2\) or \(3 x-9 \geq 3\)
- Answer
-
Add texts here. Do not delete this text first.
\(-5 x+5<-4\) or \(-5 x-5 \geq-5\)
- Answer
-
Add texts here. Do not delete this text first.
\(5 x+1<-6\) and \(3 x+9>-4\)
- Answer
-
Add texts here. Do not delete this text first.
\(7 x+2<-5\) or \(6 x-9 \geq-7\)
- Answer
-
Add texts here. Do not delete this text first.
\(-7 x-7<-2\) and \(3 x \geq 3\)
- Answer
-
Add texts here. Do not delete this text first.
\(4 x+1<0\) or \(8 x+6>9\)
- Answer
-
Add texts here. Do not delete this text first.
\(7 x+8<-3\) and \(8 x+3 \geq-9\)
- Answer
-
Add texts here. Do not delete this text first.
\(3 x<2\) and \(-7 x-8 \geq 3\)
- Answer
-
Add texts here. Do not delete this text first.
\(-5 x+2 \leq-2\) and \(-6 x+2 \geq 3\)
- Answer
-
Add texts here. Do not delete this text first.
\(4 x-1 \leq 8\) or \(3 x-9>0\)
- Answer
-
Add texts here. Do not delete this text first.
\(2 x-5 \leq 1\) and \(4 x+7>7\)
- Answer
-
Add texts here. Do not delete this text first.
\(3 x+1<0\) or \(5 x+5>-8\)
- Answer
-
Add texts here. Do not delete this text first.
\(-8 x+7 \leq 9\) or \(-5 x+6>-2\)
- Answer
-
Add texts here. Do not delete this text first.
\(x-6 \leq-5\) and \(6 x-2>-3\)
- Answer
-
Add texts here. Do not delete this text first.
\(-4 x-8<4\) or \(-4 x+2>3\)
- Answer
-
Add texts here. Do not delete this text first.
\(9 x-5<2\) or \(-8 x-5 \geq-6\)
- Answer
-
Add texts here. Do not delete this text first.
\(-9 x-5 \leq-3\) or \(x+1>3\)
- Answer
-
Add texts here. Do not delete this text first.
\(-5 x-3 \leq 6\) and \(2 x-1 \geq 6\)
- Answer
-
Add texts here. Do not delete this text first.
\(-1 \leq-7 x-3 \leq 2\)
- Answer
-
Add texts here. Do not delete this text first.
\(0<5 x-5<9\)
- Answer
-
Add texts here. Do not delete this text first.
\(5<9 x-3 \leq 6\)
- Answer
-
Add texts here. Do not delete this text first.
\(-6<7 x+3 \leq 2\)
- Answer
-
Add texts here. Do not delete this text first.
\(-2<-7 x+6<6\)
- Answer
-
Add texts here. Do not delete this text first.
\(-9<-2 x+5 \leq 1\)
- Answer
-
Add texts here. Do not delete this text first.
In Exercises 51-62, solve the given inequality for x. Graph the solution set on a number line, then use interval and set-builder notation to describe the solution set.
\(-\frac{1}{3}<\frac{x}{2}+\frac{1}{4}<\frac{1}{3}\)
- Answer
-
Add texts here. Do not delete this text first.
\(-\frac{1}{5}<\frac{x}{2}-\frac{1}{4}<\frac{1}{5}\)
- Answer
-
Add texts here. Do not delete this text first.
\(-\frac{1}{2}<\frac{1}{3}-\frac{x}{2}<\frac{1}{2}\)
- Answer
-
Add texts here. Do not delete this text first.
\(-\frac{2}{3} \leq \frac{1}{2}-\frac{x}{5} \leq \frac{2}{3}\)
- Answer
-
Add texts here. Do not delete this text first.
\(-1<x-\frac{x+1}{5}<2\)
- Answer
-
Add texts here. Do not delete this text first.
\(-2<x-\frac{2 x-1}{3}<4\)
- Answer
-
Add texts here. Do not delete this text first.
\(-2<\frac{x+1}{2}-\frac{x+1}{3} \leq 2\)
- Answer
-
Add texts here. Do not delete this text first.
\(-3<\frac{x-1}{3}-\frac{2 x-1}{5} \leq 2\)
- Answer
-
Add texts here. Do not delete this text first.
\(x<4-x<5\)
- Answer
-
Add texts here. Do not delete this text first.
\(-x<2 x+3 \leq 7\)
- Answer
-
Add texts here. Do not delete this text first.
\(-x<x+5 \leq 11\)
- Answer
-
Add texts here. Do not delete this text first.
\(−2x < 3 − x \leq 8\)
- Answer
-
Add texts here. Do not delete this text first.
Aeron has arranged for a demonstration of “How to make a Comet” by Professor O’Commel. The wise professor has asked Aeron to make sure the auditorium stays between 15 and 20 degrees Celsius (C). Aeron knows the thermostat is in Fahrenheit (F) and he also knows that the conversion formula between the two temperature scales is C = (5/9)(F − 32).
a) Setting up the compound inequality for the requested temperature range in Celsius, we get \(15 \leq C \leq 20\). Using the conversion formula above, set up the corresponding compound inequality in Fahrenheit.
b) Solve the compound inequality in part (a) for F. Write your answer in set notation.
c) What are the possible temperatures (integers only) that Aeron can set the thermostat to in Fahrenheit?
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.
Add exercises text here.
- Answer
-
Add texts here. Do not delete this text first.

