2.7E: Exercises
- Page ID
- 30299
Practice Makes Perfect
Solve Compound Inequalities with “and”
In the following exercises, solve each inequality, graph the solution, and write the solution in interval notation.
1. \(x<3\) and \(x\geq 1\)
2. \(x\leq 4\) and \(x>−2\)
- Answer
-
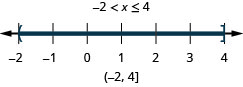
3. \(x\geq −4\) and \(x\leq −1\)
4. \(x>−6\) and \(x<−3\)
- Answer
-
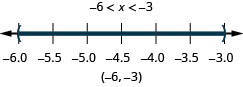
5. \(5x−2<8\) and \(6x+9\geq 3\)
6. \(4x−1<7\) and \(2x+8\geq 4\)
- Answer
-
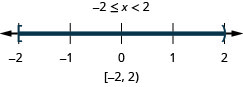
7. \(4x+6\leq 2\) and \(2x+1\geq −5\)
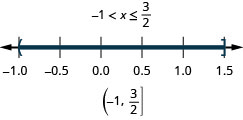
8. \(4x−2\leq 4\) and \(7x−1>−8\)
- Answer
-
9. \(2x−11<5\) and \(3x−8>−5\)
10. \(7x−8<6\) and \(5x+7>−3\)
- Answer
-
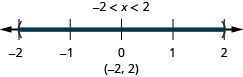
11. \(4(2x−1)\leq 12\) and \(2(x+1)<4\)
12. \(5(3x−2)\leq 5\) and \(3(x+3)<3\)
- Answer
-
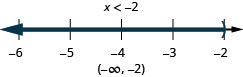
13. \(3(2x−3)>3\) and \(4(x+5)\geq 4\)
14. \(−3(x+4)<0\) and \(−1(3x−1)\leq 7\)
- Answer
-
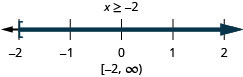
15. \(\frac{1}{2}(3x−4)\leq 1\) and \(\frac{1}{3}(x+6)\leq 4\)
16. \(\frac{3}{4}(x−8)\leq 3\) and \(\frac{1}{5}(x−5)\leq 3\)
- Answer
-
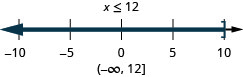
17. \(5x−2\leq 3x+4\) and \(3x−4\geq 2x+1\)
18. \(\frac{3}{4}x−5\geq −2\) and \(−3(x+1)\geq 6\)
- Answer
-
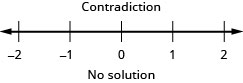
19. \(\frac{2}{3}x−6\geq −4\) and \(−4(x+2)\geq 0\)
20. \(\frac{1}{2}(x−6)+2<−5\) and \(4−\frac{2}{3}x<6\)
- Answer
-
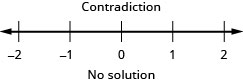
21. \(−5\leq 4x−1<7\)
22. \(−3<2x−5\leq 1\)
- Answer
-
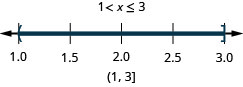
23. \(5<4x+1<9\)
24. \(−1<3x+2<8\)
- Answer
-
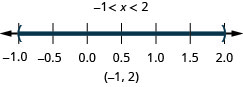
25. \(−8<5x+2\leq −3\)
26. \(−6\leq 4x−2<−2\)
- Answer
-
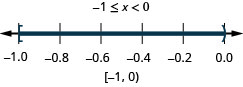
Solve Compound Inequalities with “or”
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
27. \(x\leq −2\) or \(x>3\)
28. \(x\leq −4\) or \(x>−3\)
- Answer
-
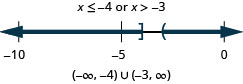
29. \(x<2\) or \(x\geq 5\)
30. \(x<0\) or \(x\geq 4\)
- Answer
-
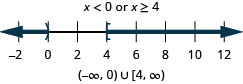
31. \(2+3x\leq 4\) or \(5−2x\leq −1\)
32. \(4−3x\leq −2\) or \(2x−1\leq −5\)
- Answer
-
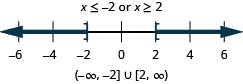
33. \(2(3x−1)<4\) or \(3x−5>1\)
34. \(3(2x−3)<−5\) or
\(4x−1>3\)
- Answer
-
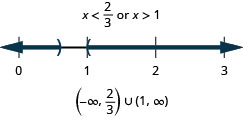
35. \(\frac{3}{4}x−2>4\) or \(4(2−x)>0\)
36. \(\frac{2}{3}x−3>5\) or \(3(5−x)>6\)
- Answer
-
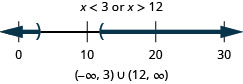
37. \(3x−2>4\) or \(5x−3\leq 7\)
38. \(2(x+3)\geq 0\) or \(3(x+4)\leq 6\)
- Answer
-
39. \(\frac{1}{2}x−3\leq 4\) or \(\frac{1}{3}(x−6)\geq −2\)
40. \(\frac{3}{4}x+2\leq −1\) or \(\frac{1}{2}(x+8)\geq −3\)
- Answer
-
Mixed practice
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
41. \(3x+7\leq 1\) and \(2x+3\geq −5\)
42. \(6(2x−1)>6\) and \(5(x+2)\geq 0\)
- Answer
-
43. \(4−7x\geq −3\) or \(5(x−3)+8>3\)
44. \(\frac{1}{2}x−5\leq 3\) or \(\frac{1}{4}(x−8)\geq −3\)
- Answer
-
45. \(−5\leq 2x−1<7\)
46. \(\frac{1}{5}(x−5)+6<4\) and \(3−\frac{2}{3}x<5\)
- Answer
-
47. \(4x−2>6\) or \(3x−1\leq −2\)
48. \(6x−3\leq 1\) and \(5x−1>−6\)
- Answer
-
49. \(−2(3x−4)\leq 2\) and \(−4(x−1)<2\)
50. \(−5\leq 3x−2\leq 4\)
- Answer
-
Solve Applications with Compound Inequalities
In the following exercises, solve.
51. Penelope is playing a number game with her sister June. Penelope is thinking of a number and wants June to guess it. Five more than three times her number is between 2 and 32. Write a compound inequality that shows the range of numbers that Penelope might be thinking of.
52. Gregory is thinking of a number and he wants his sister Lauren to guess the number. His first clue is that six less than twice his number is between four and forty-two. Write a compound inequality that shows the range of numbers that Gregory might be thinking of.
- Answer
-
\(5\leq n\leq 24\)
53. Andrew is creating a rectangular dog run in his back yard. The length of the dog run is 18 feet. The perimeter of the dog run must be at least 42 feet and no more than 72 feet. Use a compound inequality to find the range of values for the width of the dog run.
54. Elouise is creating a rectangular garden in her back yard. The length of the garden is 12 feet. The perimeter of the garden must be at least 36 feet and no more than 48 feet. Use a compound inequality to find the range of values for the width of the garden.
- Answer
-
\(6\leq w\leq 12\)
Everyday Math
55. Blood Pressure A person’s blood pressure is measured with two numbers. The systolic blood pressure measures the pressure of the blood on the arteries as the heart beats. The diastolic blood pressure measures the pressure while the heart is resting.
ⓐ Let x be your systolic blood pressure. Research and then write the compound inequality that shows you what a normal systolic blood pressure should be for someone your age.
ⓑ Let y be your diastolic blood pressure. Research and then write the compound inequality that shows you what a normal diastolic blood pressure should be for someone your age.
56. Body Mass Index (BMI) is a measure of body fat is determined using your height and weight.
ⓐ Let x be your BMI. Research and then write the compound inequality to show the BMI range for you to be considered normal weight.
ⓑ Research a BMI calculator and determine your BMI. Is it a solution to the inequality in part (a)?
- Answer
-
ⓐ answers vary ⓑ answers vary
Writing Exercises
57. In your own words, explain the difference between the properties of equality and the properties of inequality.
58. Explain the steps for solving the compound inequality \(2−7x\geq −5\) or \(4(x−3)+7>3\).
- Answer
-
Answers will vary.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?


