5.2: Add and Subtract Polynomials
- Page ID
- 5146
By the end of this section, you will be able to:
- Determine the degree of polynomials
- Add and subtract polynomials
- Evaluate a polynomial function for a given value
- Add and subtract polynomial functions
Determine the Degree of Polynomials
We have learned that a term is a constant or the product of a constant and one or more variables. A monomial is an algebraic expression with one term. When it is of the form \(ax^m\), where \(a\) is a constant and \(m\) is a whole number, it is called a monomial in one variable. Some examples of monomial in one variable are. Monomials can also have more than one variable such as and \(−4a^2b^3c^2.\)
A monomial is an algebraic expression with one term. A monomial in one variable is a term of the form \(ax^m\), where \(a\) is a constant and \(m\) is a whole number.
A monomial, or two or more monomials combined by addition or subtraction, is a polynomial. Some polynomials have special names, based on the number of terms. A monomial is a polynomial with exactly one term. A binomial has exactly two terms, and a trinomial has exactly three terms. There are no special names for polynomials with more than three terms.
- polynomial—A monomial, or two or more algebraic terms combined by addition or subtraction is a polynomial.
- monomial—A polynomial with exactly one term is called a monomial.
- binomial—A polynomial with exactly two terms is called a binomial.
- trinomial—A polynomial with exactly three terms is called a trinomial.
Here are some examples of polynomials.
| Polynomial | \(y+1\) | \(4a^2−7ab+2b^2\) | \(4x^4+x^3+8x^2−9x+1\) | |
|---|---|---|---|---|
| Monomial | \(14\) | \(8y^2\) | \(−9x^3y^5\) | \(−13a^3b^2c\) |
| Binomial | \(a+7ba+7b\) | \(4x^2−y^2\) | \(y^2−16\) | \(3p^3q−9p^2q\) |
| Trinomial | \(x^2−7x+12\) | \(9m^2+2mn−8n^2\) | \(6k^4−k^3+8k\) | \(z^4+3z^2−1\) |
Notice that every monomial, binomial, and trinomial is also a polynomial. They are just special members of the “family” of polynomials and so they have special names. We use the words monomial, binomial, and trinomial when referring to these special polynomials and just call all the rest polynomials.
The degree of a polynomial and the degree of its terms are determined by the exponents of the variable. A monomial that has no variable, just a constant, is a special case. The degree of a constant is 0.
- The degree of a term is the sum of the exponents of its variables.
- The degree of a constant is 0.
- The degree of a polynomial is the highest degree of all its terms.
Let’s see how this works by looking at several polynomials. We’ll take it step by step, starting with monomials, and then progressing to polynomials with more terms. Let's start by looking at a monomial. The monomial \(8ab^2\) has two variables \(a\) and \(b\). To find the degree we need to find the sum of the exponents. The variable a doesn't have an exponent written, but remember that means the exponent is 1. The exponent of \(b\) is 2. The sum of the exponents, 1+2,1+2, is 3 so the degree is 3.
Here are some additional examples.
Working with polynomials is easier when you list the terms in descending order of degrees. When a polynomial is written this way, it is said to be in standard form of a polynomial. Get in the habit of writing the term with the highest degree first.
Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial. Then, find the degree of each polynomial.
- \(7y2−5y+3\)
- \(−2a^4b^2\)
- \(3x5−4x3−6x2+x−8\)
- \(2y−8xy^3\)
- \(15\)
- Answer
-
Polynomial Number of terms Type Degree of terms Degree of polynomial ⓐ \(7y^2−5y+3\) 3 Trinomial 2, 1, 0 2 ⓑ \(−2a^4b^2−2a^4b^2\) 1 Monomial 4, 2 6 ⓒ \(3x5−4x3−6x2+x−8\) 5 Polynomial 5, 3, 2, 1, 0 5 ⓓ \(2y−8xy^3\) 2 Binomial 1, 4 4 ⓔ \(15\) 1 Monomial 0 0
Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial. Then, find the degree of each polynomial.
- \(−5\)
- \(8y^3−7y^2−y−3\)
- \(−3x^2y−5xy+9xy^3\)
- \(81m^2−4n^2\)
- \(−3x^6y^3z\)
- Answer a
-
monomial, 0
- Answer b
-
polynomial, 3
- Answer c
-
trinomial, 3
- Answer d
-
binomial, 2
- Answer b
-
monomial, 10
Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial. Then, find the degree of each polynomial.
- \(64k^3−8\)
- \(9m^3+4m^2−2\)
- \(56\)
- \(8a^4−7a^3b−6a^2b^2−4ab^3+7b^4\)
- \(-p^4q^3\)
- Answer
-
ⓐbinomial, 3 ⓑ trinomial, 3 ⓒ monomial, 0 ⓓ polynomial, 4 ⓔ monomial, 7
Add and Subtract Polynomials
We have learned how to simplify expressions by combining like terms. Remember, like terms must have the same variables with the same exponent. Since monomials are terms, adding and subtracting monomials is the same as combining like terms. If the monomials are like terms, we just combine them by adding or subtracting the coefficients.
Add or subtract:
- \(25y^2+15y^2\)
- \(16pq^3−(−7pq^3)\).
- Answer a
-
\( \begin{array} {ll} {} &{25y^2+15y^2} \\ {\text{Combine like terms.}} &{40y^2} \\ \end{array} \nonumber \)
- Answer b
-
\( \begin{array} {ll} {} &{16pq^3−(−7pq^3)} \\ {\text{Combine like terms.}} &{23pq^3} \\ \end{array} \nonumber \)
Add or subtract:
- \(12q^2+9q^2\)
- \(8mn^3−(−5mn^3)\).
- Answer
-
ⓐ \(21q^2\) ⓑ \(13mn^3\)
Add or subtract:
- \(−15c^2+8c^2\)
- \(−15y^2z^3−(−5y^2z^3)\)
- Answer
-
ⓐ \(−7c^2\) ⓑ \(−10y^2z^3\)
Remember that like terms must have the same variables with the same exponents.
Simplify:
- \(a^2+7b^2−6a^2\)
- \(u^2v+5u^2−3v^2\)
- Answer
-
ⓐ Combine like terms.
\(a^2+7b^2−6a^2 \;=\; −5a^2+7b^2\)ⓑ There are no like terms to combine. In this case, the polynomial is unchanged.
\(u^2v+5u^2−3v^2\)
Add:
- \(8y^2+3z^2−3y^2\)
- \(m^2n^2−8m^2+4n^2\)
- Answer
-
ⓐ \(5y^2+3z^2\)
ⓑ \(m^2n^2−8m^2+4n^2\)
Add:
- \(3m^2+n^2−7m^2\)
- \(pq^2−6p−5q^2\)
- Answer
-
ⓐ \(−4m^2+n^2\)
ⓑ \(pq^2−6p−5q^2\)
We can think of adding and subtracting polynomials as just adding and subtracting a series of monomials. Look for the like terms—those with the same variables and the same exponent. The Commutative Property allows us to rearrange the terms to put like terms together.
Find the sum: \((7y^2−2y+9)\;+\;(4y^2−8y−7)\).
- Answer
-
\(\begin{align*} &\text{Identify like terms.} & & (\underline{\underline{7y^2}}−\underline{2y}+9)+(\underline{\underline{4y^2}}−\underline{8y}−7) \\[6pt]
&\text{Rewrite without the parentheses,} \\
&\text{rearranging to get the like terms together.} & & \underline{\underline{7y^2+4y^2}}−\underline{2y−8y}+9−7\\[6pt]
&\text{Combine like terms.} & & 11y^2−10y+2 \end{align*} \)
Find the sum: \( (7x^2−4x+5)\;+\;(x^2−7x+3)\)
- Answer
-
\(8x^2−11x+8\)
Find the sum: \((14y^2+6y−4)\;+\;(3y^2+8y+5)\)
- Answer
-
\(17y^2+14y+1\)
Be careful with the signs as you distribute while subtracting the polynomials in the next example.
Find the difference: \((9w^2−7w+5)\;−\;(2w^2−4)\)
- Answer
-
\(\begin{align*} & & & (9w^2−7w+5)\;−\;(2w^2−4) \\[6pt]
&\text{Distribute and identify like terms.} & & \underline{\underline{9w^2}}−\underline{7w}+5-\underline{\underline{2w^2}}+4 \\[6pt]
&\text{Rearrange the terms.} & & \underline{\underline{9w^2-2w^2}}−\underline{7w}+5+4\\[6pt]
&\text{Combine like terms.} & & 7w^2−7w+9 \end{align*} \)
Find the difference: \((8x^2+3x−19)\;−\;(7x^2−14)\)
- Answer
-
\(x^2+3x−5\)
Find the difference: \((9b^2−5b−4)\;−\;(3b^2−5b−7)\)
- Answer
-
\(6b^2+3\)
Subtract \((p^2+10pq−2q^2)\) from \((p^2+q^2)\).
- Answer
-
\(\begin{align*} & & & (p^2+q^2)\;−\;(p^2+10pq−2q^2) \\[6pt]
&\text{Distribute and identify like terms.} & & \underline{\underline{p^2}}+\underline{q^2}-\underline{\underline{p^2}}-10pq + \underline{2q^2} \\[6pt]
&\text{Rearrange the terms, putting like terms together.} & & \underline{\underline{p^2-p^2}}−10pq +\underline{q^2 + 2q^2}\\[6pt]
&\text{Combine like terms.} & & −10pq+3q^2 \end{align*} \)
Subtract \((a^2+5ab−6b^2)\) from \((a^2+b^2)\)
- Answer
-
\(−5ab+7b^2\)
Subtract \((m^2−7mn−3n^2)\) from \((m^2+n^2)\).
- Answer
-
7mn+4n^2
Find the sum: \((u^2−6uv+5v^2)\;+\;(3u^2+2uv)\)
- Answer
-
\(\begin{align*} & & & (u^2−6uv+5v^2)\;+\;(3u^2+2uv) \\[6pt]
&\text{Distribute and identify like terms.} & & \underline{\underline{u^2}}-\underline{6uv}+5v^2+\underline{\underline{3u^2}}+ \underline{2uv} \\[6pt]
&\text{Rearrange the terms to put like terms together.} & & \underline{\underline{u^2}}+\underline{\underline{3u^2}}- \underline{6uv}+ \underline{2uv}+5v^2\\[6pt]
&\text{Combine like terms.} & & 4u^2−4uv+5v^2 \end{align*} \)
Find the sum: \((3x^2−4xy+5y^2)\;+\;(2x^2−xy)\)
- Answer
-
\(5x^2−5xy+5y^2\)
Find the sum: \((2x^2−3xy−2y^2)\;+\;(5x^2−3xy)\)
- Answer
-
\(7x^2−6xy−2y^2\)
When we add and subtract more than two polynomials, the process is the same.
Simplify: \((a^3−a^2b)\;−\;(ab^2+b^3)\;+\;(a^2b+ab^2)\)
- Answer
-
\(\begin{align*} & & & (a^3−a^2b)\;−\;(ab^2+b^3)\;+\;(a^2b+ab^2) \\[6pt]
&\text{Distribute} & & a^3−a^2b − ab^2 - b^3 + a^2b+ab^2\\[6pt]
&\text{Rearrange the terms to put like terms together.} & & a^3−a^2b + a^2b− ab^2 + ab^2 - b^3 \\[6pt]
&\text{Combine like terms.} & & a^3−b^3 \end{align*} \)
Simplify: \((x^3−x^2y)\;−\;(xy^2+y^3)\;+\;(x^2y+xy^2)\)
- Answer
-
\(x^3+y^3\)
Simplify: \((p^3−p^2q)\;+\;(pq^2+q^3)\;−\;(p^2q+pq^2)\)
- Answer
-
\(p^3−3p^2q+q^3\)
Evaluate a Polynomial Function for a Given Value
A polynomial function is a function defined by a polynomial. For example, \(f(x)=x^2+5x+6\) and \(g(x)=3x−4\) are polynomial functions, because \(x^2+5x+6\) and \(3x−4\) are polynomials.
A polynomial function is a function whose range values are defined by a polynomial.
In Graphs and Functions, where we first introduced functions, we learned that evaluating a function means to find the value of \(f(x)\) for a given value of \(x\). To evaluate a polynomial function, we will substitute the given value for the variable and then simplify using the order of operations.
For the function \(f(x)=5x^2−8x+4\) find:
- \(f(4)\)
- \(f(−2)\)
- \(f(0)\).
- Answer
-
ⓐ
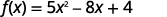
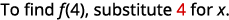
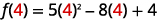
Simplify the exponents.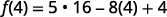 
Multiply.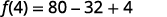 
Simplify. 
ⓑ
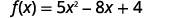
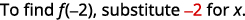
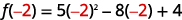
Simplify the exponents.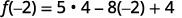 
Multiply.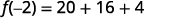 
Simplify. 
ⓒ
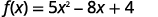
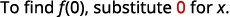
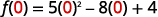
Simplify the exponents. 
Multiply.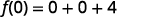 
For the function \(f(x)=3x^2+2x−15\), find
- \(f(3)\)
- \(f(−5)\)
- \(f(0)\).
- Answer
-
ⓐ 18 ⓑ 50 ⓒ \(−15\)
For the function \(g(x)=5x^2−x−4\), find
- \(g(−2)\)
- \(g(−1)\)
- \(g(0)\).
- Answer
-
ⓐ 20 ⓑ 2 ⓒ \(−4\)
The polynomial functions similar to the one in the next example are used in many fields to determine the height of an object at some time after it is projected into the air. The polynomial in the next function is used specifically for dropping something from 250 ft.
The polynomial function \(h(t)=−16t^2+250\) gives the height of a ball t seconds after it is dropped from a 250-foot tall building. Find the height after \(t=2\) seconds.
- Answer
-
\( \begin{array} {ll} {} &{h(t)=−16t^2+250} \\ {} &{} \\ {\text{To find }h(2)\text{, substitute }t=2.} &{h(2)=−16(2)^2+250} \\ {\text{Simplify.}} &{h(2)=−16·4+250} \\ {} &{}\\ {\text{Simplify.}} &{h(2)=−64+250} \\ {} &{} \\ {\text{Simplify.}} &{h(2)=186} \\ {} &{\text{After 2 seconds the height of the ball is 186 feet.}} \\ \end{array} \nonumber \)
The polynomial function \(h(t)=−16t^2+150\) gives the height of a stone t seconds after it is dropped from a 150-foot tall cliff. Find the height after \(t=0\) seconds (the initial height of the object).
- Answer
-
The height is \(150\) feet.
The polynomial function \(h(t)=−16t^2+175\) gives the height of a ball t seconds after it is dropped from a 175-foot tall bridge. Find the height after \(t=3\) seconds.
- Answer
-
The height is \(31\) feet.
Add and Subtract Polynomial Functions
Just as polynomials can be added and subtracted, polynomial functions can also be added and subtracted.
For functions \(f(x)\) and \(g(x)\),
\[(f+g)(x)=f(x)+g(x)\]
\[(f−g)(x)=f(x)−g(x)\]
For functions \(f(x)=3x^2−5x+7\) and \(g(x)=x^2−4x−3\), find:
- \((f+g)(x)\)
- \((f+g)(3)\)
- \((f−g)(x)\)
- \((f−g)(−2)\).
- Answer
-
ⓐ
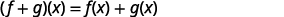
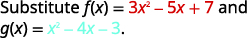
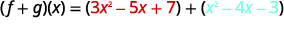
Rewrite without the parentheses.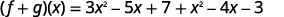 
Put like terms together.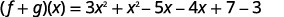 
Combine like terms.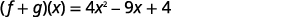 
ⓑ In part (a) we found \((f+g)(x)\) and now are asked to find \((f+g)(3)\).
\( \begin{array} {ll} {} &{(f+g)(x)=4x^2−9x+4} \\ {} &{} \\ {\text{To find }(f+g)\space(3),\text{ substitute }x=3.} &{(f+g)(3)=4(3)^2−9·3+4} \\ {} &{} \\ {} &{(f+g)(3)=4·9−9·3+4} \\ {} &{} \\ {} &{(f+g)(3)=36−27+4} \\ \end{array} \nonumber \)
Notice that we could have found \((f+g)(3)\) by first finding the values of \(f(3)\) and \(g(3)\) separately and then adding the results.
Find \(f(3)\).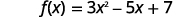 
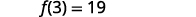
Find \(g(3)\).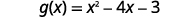 
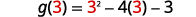
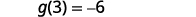
Find \((f+g)(3)\).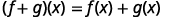 
ⓒ
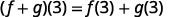
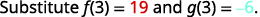
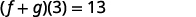
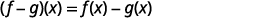
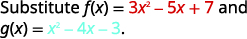
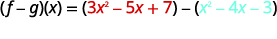
Rewrite without the parentheses.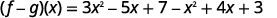 
Put like terms together.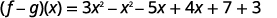 
Combine like terms.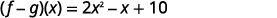 
ⓓ
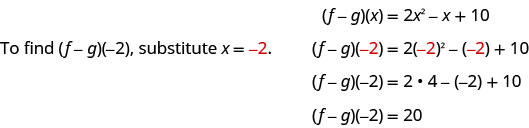
For functions \(f(x)=2x^2−4x+3\) and \(g(x)=x^2−2x−6\), find: ⓐ \((f+g)(x)\) ⓑ \((f+g)(3)\) ⓒ \((f−g)(x)\) ⓓ \((f−g)(−2)\).
- Answer
-
ⓐ \((f+g)(x)=3x^2−6x−3\)
ⓑ \((f+g)(3)=6\)
ⓒ \((f−g)(x)=x^2−2x+9\)
ⓓ \((f−g)(−2)=17\)
For functions \(f(x)=5x^2−4x−1\) and \(g(x)=x^2+3x+8\), find ⓐ \((f+g)(x)\) ⓑ \((f+g)(3)\) ⓒ \((f−g)(x)\) ⓓ \((f−g)(−2)\).
- Answer
-
ⓐ \((f+g)(x)=6x^2−x+7\)
ⓑ \((f+g)(3)=58\)
ⓒ \((f−g)(x)=4x^2−7x−9\)
ⓓ \((f−g)(−2)=21\)
Access this online resource for additional instruction and practice with adding and subtracting polynomials.
- Adding and Subtracting Polynomials
Key Concepts
- Monomial
- A monomial is an algebraic expression with one term.
- A monomial in one variable is a term of the form axm,axm, where a is a constant and m is a whole number.
- Polynomials
- Polynomial—A monomial, or two or more algebraic terms combined by addition or subtraction is a polynomial.
- monomial —A polynomial with exactly one term is called a monomial.
- binomial — A polynomial with exactly two terms is called a binomial.
- trinomial —A polynomial with exactly three terms is called a trinomial.
- Degree of a Polynomial
- The degree of a term is the sum of the exponents of its variables.
- The degree of a constant is 0.
- The degree of a polynomial is the highest degree of all its terms.
Glossary
- binomial
- A binomial is a polynomial with exactly two terms.
- degree of a constant
- The degree of any constant is 0.
- degree of a polynomial
- The degree of a polynomial is the highest degree of all its terms.
- degree of a term
- The degree of a term is the sum of the exponents of its variables.
- monomial
- A monomial is an algebraic expression with one term. A monomial in one variable is a term of the form axm,axm, where a is a constant and m is a whole number.
- polynomial
- A monomial or two or more monomials combined by addition or subtraction is a polynomial.
- standard form of a polynomial
- A polynomial is in standard form when the terms of a polynomial are written in descending order of degrees.
- trinomial
- A trinomial is a polynomial with exactly three terms.
- polynomial function
- A polynomial function is a function whose range values are defined by a polynomial.