3.2E: Exercises

Last updated
Save as PDF

Page ID: 30301

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Plot Points in a Rectangular Coordinate System

In the following exercises, plot each point in a rectangular coordinate system and identify the quadrant in which the point is located.

1. a. $(−4,2)$ b. $(−1,−2)$ c. $(3,−5)$ d. $(−3,0)$
e. $(53,2)$

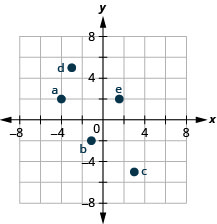
Answer: $This figure shows points plotted on the x y-coordinate plane. The x and y axes run from negative 6 to 6. The point labeled a is 4 units to the left of the origin and 2 units above the origin and is located in quadrant II. The point labeled b is 1 unit to the left of the origin and 2 units below the origin and is located in quadrant III. The point labeled c is 3 units to the right of the origin and 5 units below the origin and is located in quadrant IV. The point labeled d is 3 units to the left of the origin and 5 units above the origin and is located in quadrant II. The point labeled e is 1 and a half units to the right of the origin and 2 units above the origin and is located in quadrant I.$

2. a. $(−2,−3)$ b. $(3,−3)$ c. $(−4,1)$ d. $(4,−1)$
e. $(32,1)$

3. a. $(3,−1)$ b. $(−3,1)$ c. $(−2,0)$ d. $(−4,−3)$
e. $(1,145)$

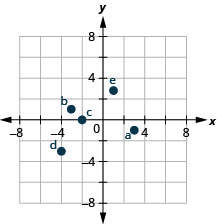
Answer: $This figure shows points plotted on the x y-coordinate plane. The x and y axes run from negative 6 to 6. The point labeled a is 3 units to the right of the origin and 1 unit below the origin and is located in quadrant IV. The point labeled b is 3 units to the left of the origin and 1 unit above the origin and is located in quadrant II. The point labeled c is 2 units to the left of the origin and 2 units above the origin and is located in quadrant II. The point labeled d is 4 units to the left of the origin and 3 units below the origin and is located in quadrant III. The point labeled e is 1 unit to the right of the origin and 3 and 4 fifths units above the origin and is located in quadrant I.$

4. a. $(−1,1)$ b. $(−2,−1)$ c. $(2,0)$ d. $(1,−4)$
e. $(3,72)$

In the following exercises, for each ordered pair, decide

a. is the ordered pair a solution to the equation? b. is the point on the line?

5. $y=x+2$;

A: $(0,2)$; B: $(1,2)$; C: $(−1,1)$; D: $(−3,−1)$.

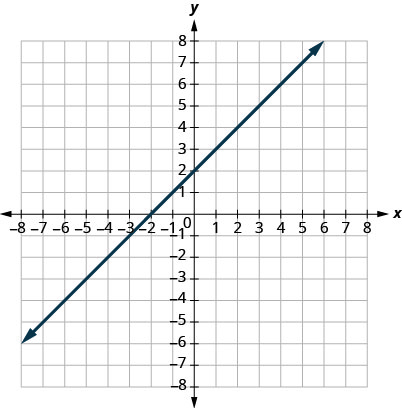
$This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 3, negative 1), (negative 2, 0), (negative 1, 1), (0, 2), (1, 3), (2, 4), and (3, 5).$

Answer: a. A: yes, B: no, C: yes, D: yes b. A: yes, B: no, C: yes, D: yes

6. $y=x−4$;

A: $(0,−4)$; B: $(3,−1)$; C: $(2,2)$; D: $(1,−5)$.

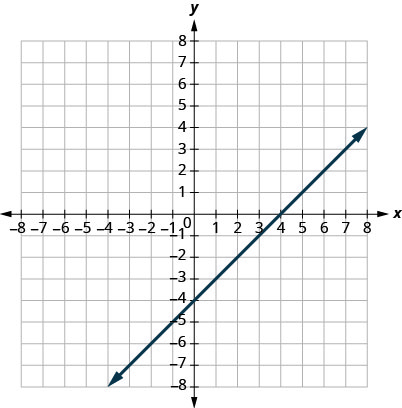
$This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 3, negative 7), (negative 2, negative 6), (negative 1, negative 5), (0, negative 4), (1, negative 3), (2, negative 2), and (3, negative 1).$

7. $y=12x−3$;
A: $(0,−3)$; B: $(2,−2)$; C: $(−2,−4)$; D: $(4,1)$.

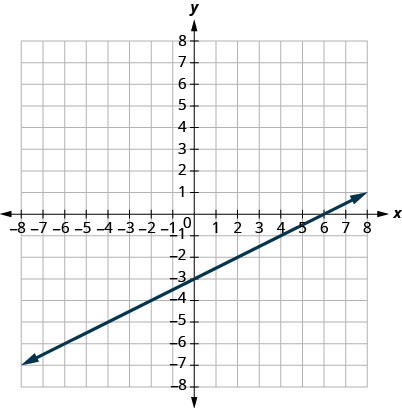
$This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 4, negative 5), (negative 2, negative 4), (0, negative 3), (2, negative 2), (4, negative 1), and (6, 0).$

Answer: a. A: yes, B: yes, C: yes, D: no b. A: yes, B: yes, C: yes, D: no

8. $y=13x+2$;
A: $(0,2)$; B: $(3,3)$; C: $(−3,2)$; D: $(−6,0)$.

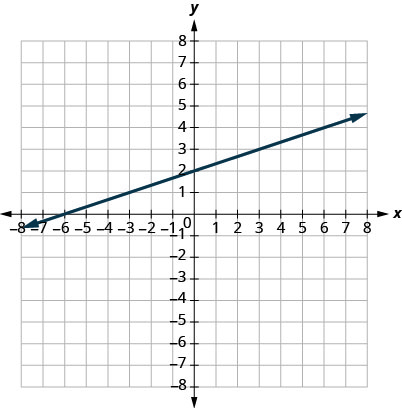
$This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 6, 0), (negative 3, 1), (0, 2), (3, 3), (6, 4), and (9, 5).$

Graph a Linear Equation by Plotting Points

In the following exercises, graph by plotting points.

9. $y=x+2$

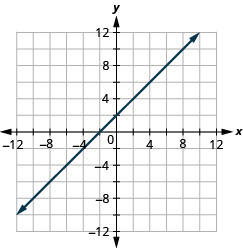
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 3, negative 1), (negative 2, 0), (negative 1, 1), (0, 2), (1, 3), (2, 4), and (3, 5).$

10. $y=x−3$

11. $y=3x−1$

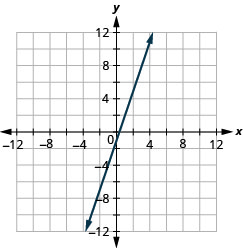
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 3, negative 10), (negative 2, negative 7), (negative 1, negative 4), (0, negative 1), (1, 2), (2, 5), (3, 8), and (4, 11).$

12. $y=−2x+2$

13. $y=−x−3$

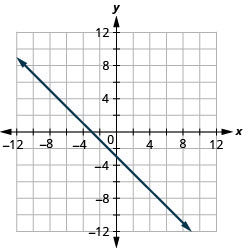
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 3, 0), (negative 2, negative 1), (negative 1, negative 2), (0, negative 3), (1, negative 4), (2, negative 5), (3, negative 6), and (4, negative 7).$

14. $y=−x−2$

15. $y=2x$

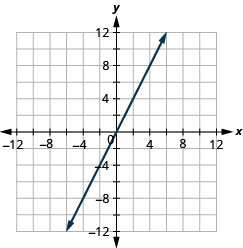
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 3, negative 6), (negative 2, negative 4), (negative 1, negative 2), (0, 0), (1, 2), (2, 4), and (3, 6).$

16. $y=−2x$

17. $y=12x+2$

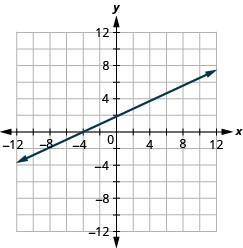
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 6, negative 2), (negative 4, 0), (negative 2, 1), (0, 2), (2, 3), (4, 4), and (6, 5).$

18. $y=13x−1$

19. $y=43x−5$

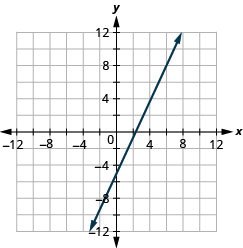
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 3, negative 9), (0, negative 5), (3, negative 1), (6, 3), and (9, 7).$

20. $y=32x−3$

21. $y=−25x+1$

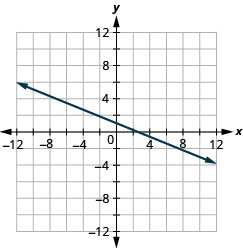
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 10, 5), (negative 5, 3), (0, 1), (5, negative 1), and (10, negative 3).$

22. $y=−45x−1$

23. $y=−32x+2$

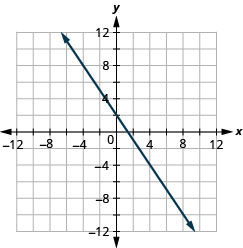
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 4, 8), (negative 2, 5), (0, 2), (2, negative 1), (4, negative 4), and (6, negative 7).$

24. $y=−53x+4$

Graph Vertical and Horizontal lines

In the following exercises, graph each equation.

25. a. $x=4$ b. $y=3$

Answer

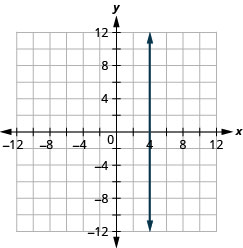
$This figure shows a vertical straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (4, negative 1), (4, 0), and (4, 1).$

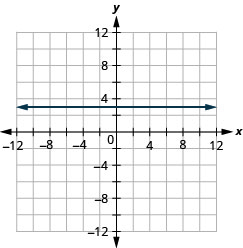
$This figure shows a horizontal straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 1, 3), (0, 3), and (1, 3).$

26. a. $x=3$ b. $y=1$

27. a. $x=−2$ b. $y=−5$

Answer

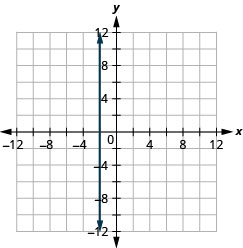
$This figure shows a vertical straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 2, negative 1), (negative 2, 0), and (negative 2, 1).$

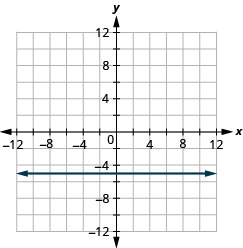
$This figure shows a horizontal straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 12 to 12. The line goes through the points (negative 1, negative 5), (0, negative 5), and (1, negative 5).$

28. a. $x=−5$ b. $y=−2$

In the following exercises, graph each pair of equations in the same rectangular coordinate system.

29. $y=2x$ and $y=2$

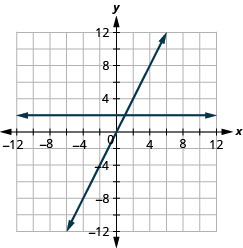
Answer: $The figure shows the graphs of a straight horizontal line and a straight slanted line on the same x y-coordinate plane. The x and y axes run from negative 12 to 12. The horizontal line goes through the points (0, 2), (1, 2), and (2, 2). The slanted line goes through the points (0, 0), (1, 2), and (2, 4).$

30. $y=5x$ and $y=5$

31. $y=−12x$ and $y=−12$

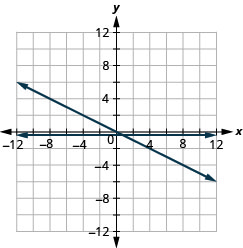
Answer: $The figure shows the graphs of a straight horizontal line and a straight slanted line on the same x y-coordinate plane. The x and y axes run from negative 12 to 12. The horizontal line goes through the points (0, negative 1 divided 2), (1, negative 1 divided 2), and (2, negative 1 divided 2). The slanted line goes through the points (0, 0), (1, negative 1 divided 2), and (2, negative 1).$

32. $y=−13x$ and $y=−13$

Find x- and y-Intercepts

In the following exercises, find the x- and y-intercepts on each graph.

33.
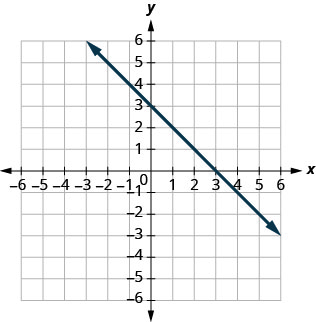
$The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 6, 9), (negative 3, 6), (0, 3), (3, 0), and (6, negative 3).$

Answer: $(3,0),(0,3)$

34.
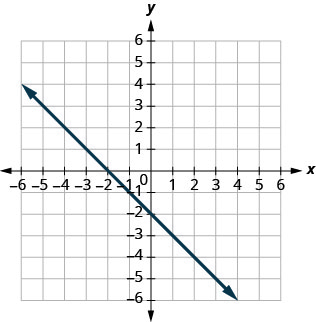
$The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 6, 4), (negative 4, 2), (negative 2, 0), (0, negative 2), (2, negative 4), and (4, negative 6).$

35.
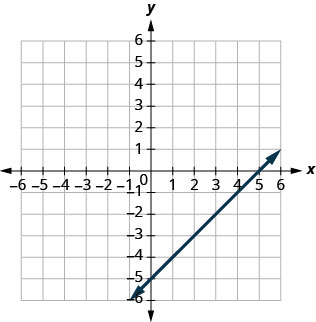
$The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 1, negative 6), (0, negative 5), (2, negative 3), (5, 0), and (7, 2).$

Answer: $(5,0),(0,−5)$

36.
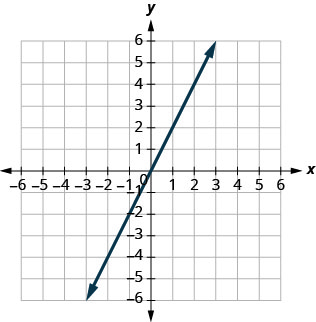
$The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 2, negative 4), (negative 1, negative 2), (0, 0), (1, 2), and (2, 4).$

In the following exercises, find the intercepts for each equation.

37. $x−y=5$

Answer: $x$-int: $(5,0)$, $y$-int: $(0,−5)$

38. $x−y=−4$

39. $3x+y=6$

Answer: $x$-int: $(2,0)$, $y$-int: $(0,6)$

40. $x−2y=8$

41. $4x−y=8$

Answer: $x$-int: $(2,0)$, $y$-int: $(0,−8)$

42. $5x−y=5$

43. $2x+5y=10$

Answer: $x$-int: $(5,0)$, $y$-int: $(0,2)$

44. $3x−2y=12$

Graph a Line Using the Intercepts

In the following exercises, graph using the intercepts.

45. $−x+4y=8$

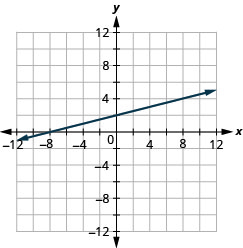
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 12 to 12. The line goes through the points (negative 8, 0), (0, 2), (4, 3), and (8, 4).$

46. $x+2y=4$

47. $x+y=−3$

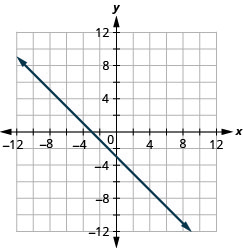
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 12 to 12. The line goes through the points (negative 3, 0), (0, negative 3), and (3, negative 6).$

48. $x−y=−4$

49. $4x+y=4$

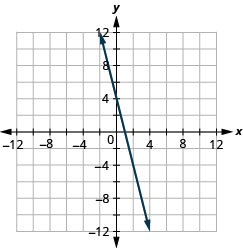
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 12 to 12. The line goes through the points (0, 4), (1, 0), and (2, negative 4).$

50. $3x+y=3$

51. $3x−y=−6$

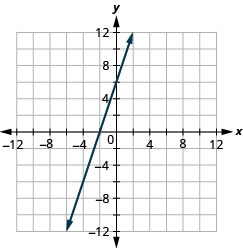
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 12 to 12. The line goes through the points (negative 2, 0), (negative 1, 3), and (0, 6).$

52. $2x−y=−8$

53. $2x+4y=12$

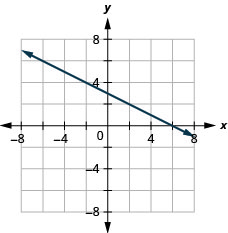
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (0, 3), (2, 2), and (6, 0).$

54. $3x−2y=6$

55. $2x−5y=−20$

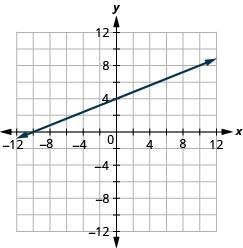
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 12 to 12. The line goes through the points (negative 10, 0), (0, 4), and (10, 8).$

56. $3x−4y=−12$

57. $y=−2x$

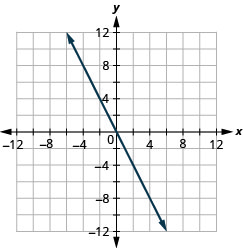
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 12 to 12. The line goes through the points (negative 1, 2), (0, 0), and (1, negative 2).$

58. $y=5x$

59. $y=x$

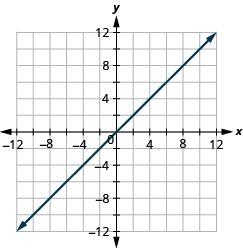
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 12 to 12. The line goes through the points (negative 1, negative 1), (0, 0), and (1, 1).$

60. $y=−x$

Mixed Practice

In the following exercises, graph each equation.

61. $y=32x$

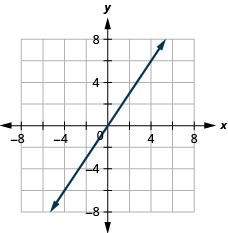
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 2, negative 3), (0, 0), and (2, 3).$

62. $y=−23x$

63. $y=−12x+3$

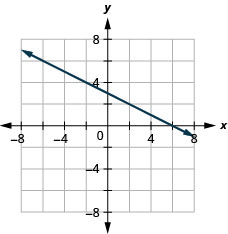
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 2, 4), (0, 3), (2, 2), (4, 1), and (6, 0).$

64. $y=14x−2$

65. $4x+y=2$

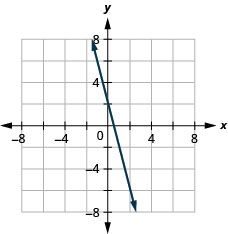
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 1, 6), (0, 2), (1, negative 2), and (2, negative 4).$

66. $5x+2y=10$

67. $y=−1$

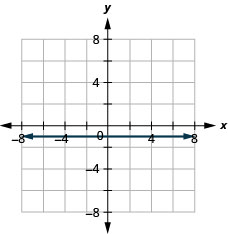
Answer: $The figure shows a horizontal straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 2, negative 1), (0, negative 1), and (1, negative 1).$

68. $x=3$

Writing Exercises

69. Explain how you would choose three x-values to make a table to graph the line $y=15x−2$.

Answer: Answers will vary.

70. What is the difference between the equations of a vertical and a horizontal line?

71. Do you prefer to use the method of plotting points or the method using the intercepts to graph the equation $4x+y=−4$? Why?

Answer: Answers will vary.

72. Do you prefer to use the method of plotting points or the method using the intercepts to graph the equation $y=23x−2$? Why?

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

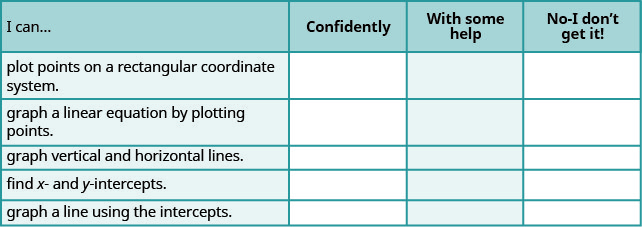
$This table has 6 rows and 4 columns. The first row is a header row and it labels each column. The first column header is “I can…”, the second is “Confidently”, the third is “With some help”, and the fourth is “No, I don’t get it”. Under the first column are the phrases “plot points on a rectangular coordinate system”, “graph a linear equation by plotting points”, “graph vertical and horizontal lines”, “find x and y intercepts”, and “graph a line using intercepts”. The other columns are left blank so that the learner may indicate their mastery level for each topic.$

b. If most of your checks were:

Confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

With some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

No, I don’t get it. This is a warning sign and you must address it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

Search

Text Color

Text Size

Margin Size

Font Type