7.2: Multiply and Divide Rational Expressions
- Page ID
- 5160
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Determine the values for which a rational expression is undefined
- Simplify rational expressions
- Multiply rational expressions
- Divide rational expressions
- Multiply and divide rational functions
We previously reviewed the properties of fractions and their operations. We introduced rational numbers, which are just fractions where the numerators and denominators are integers. In this chapter, we will work with fractions whose numerators and denominators are polynomials. We call this kind of expression a rational expression.
A rational expression is an expression of the form \(\dfrac{p}{q}\), where \(p\) and \(q\) are polynomials and \(q\neq 0\).
Here are some examples of rational expressions:
\[−\dfrac{24}{56} \qquad \dfrac{5x}{12y} \qquad \dfrac{4x+1}{x^2−9} \qquad \dfrac{4x^2+3x−1}{2x−8}\nonumber\]
Notice that the first rational expression listed above, \(−\dfrac{24}{56}\), is just a fraction. Since a constant is a polynomial with degree zero, the ratio of two constants is a rational expression, provided the denominator is not zero.
We will do the same operations with rational expressions that we did with fractions. We will simplify, add, subtract, multiply, divide and use them in applications.
Determine the Values for Which a Rational Expression is Undefined
If the denominator is zero, the rational expression is undefined. The numerator of a rational expression may be 0—but not the denominator.
When we work with a numerical fraction, it is easy to avoid dividing by zero because we can see the number in the denominator. In order to avoid dividing by zero in a rational expression, we must not allow values of the variable that will make the denominator be zero.
So before we begin any operation with a rational expression, we examine it first to find the values that would make the denominator zero. That way, when we solve a rational equation for example, we will know whether the algebraic solutions we find are allowed or not.
- Set the denominator equal to zero.
- Solve the equation.
Determine the value for which each rational expression is undefined:
a. \(\dfrac{8a^2b}{3c}\) b. \(\dfrac{4b−3}{2b+5}\) c. \(\dfrac{x+4}{x^2+5x+6}\).
Solution
The expression will be undefined when the denominator is zero.
a.
\(\begin{array} {ll} &\dfrac{8a^2b}{3c} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve} \\ \text{for the variable.} \end{array} &3c=0 \\ &c=0 \\ &\dfrac{8a^2b}{3c}\text{ is undefined for }c=0 \end{array} \)
b.
\(\begin{array} {ll} &\dfrac{4b-3}{2b+5} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve} \\ \text{for the variable.} \end{array} &2b+5=0 \\ &2b=-5 \\ &b=-\dfrac{5}{2} \\ & \\ &\dfrac{4b-3}{2b+5} \text{ is undefined for }b=-\dfrac{5}{2} \end{array} \)
c.
\(\begin{array} {ll} &\dfrac{x+4}{x^2 + 5x + 6} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve } \\ \text{for the variable.} \end{array} &x^2+5x+6=0 \\ &(x+2)(x+3)=0 \\ &x+2=0\text{ or }x+3=0 \\ &x=-2\text{ or }x=-3 \\ & \\ &\dfrac{x+4}{x^2+5x+6}\text{ is undefined for }x=-2\text{ or }x=-3 \end{array} \)
Determine the value for which each rational expression is undefined.
a. \(\dfrac{3y^2}{8x}\) b. \(\dfrac{8n−5}{3n+1}\) c. \(\dfrac{a+10}{a^2+4a+3}\)
- Answer
-
a. \(x=0\)
b. \(n=−\dfrac{1}{3}\)
c. \(a=−1,a=−3\)
Determine the value for which each rational expression is undefined.
a.\(\dfrac{4p}{5q}\) b. \(\dfrac{y−1}{3y+2}\) c. \(\dfrac{m−5}{m^2+m−6}\)
- Answer
-
a. \(q=0\)
b. \(y=−\dfrac{2}{3}\)
c. \(m=2,m=−3\)
Simplify Rational Expressions
A fraction is considered simplified if there are no common factors, other than 1, in its numerator and denominator. Similarly, a simplified rational expression has no common factors, other than 1, in its numerator and denominator.
A rational expression is considered simplified if there are no common factors in its numerator and denominator.
For example,
\[ \begin{array} {l} \dfrac{x+2}{x+3} \text{ is simplified because there are no common factors of } x+2 \text{ and }x+3. \\ \dfrac{2x}{3x} \text{ is not simplified because x is a common factor of }2x\text{ and }3x. \\ \end{array} \nonumber\]
We use the Equivalent Fractions Property to simplify numerical fractions. We restate it here as we will also use it to simplify rational expressions.
If \(a\), \(b\), and \(c\) are numbers where \(b\neq 0,c\neq 0,\)
\[\text {then } \dfrac{a}{b}=\dfrac{a·c}{b·c} \text{ and } \dfrac{a·c}{b·c}=\dfrac{a}{b}\nonumber\]
Notice that in the Equivalent Fractions Property, the values that would make the denominators zero are specifically disallowed. We see \(b\neq 0,c\neq 0\) clearly stated.
To simplify rational expressions, we first write the numerator and denominator in factored form. Then we remove the common factors using the Equivalent Fractions Property.
Be very careful as you remove common factors. Factors are multiplied to make a product. You can remove a factor from a product. You cannot remove a term from a sum.

Removing the \(x\)'s from \(\dfrac{x+5}{x}\) would be like cancelling the \(2\)’s in the fraction \(\dfrac{2+5}{2}!\)
How to Simplify a Rational Expression
Simplify: \(\dfrac{x^2+5x+6}{x^2+8x+12}\)
Solution
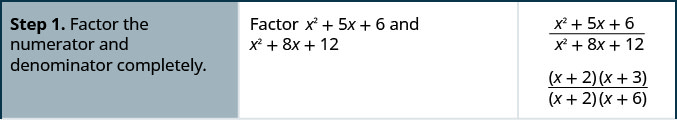

Simplify: \(\dfrac{x^2−x−2}{x^2−3x+2}\).
- Answer
-
\(\dfrac{x+1}{x−1},x\neq 2,x\neq 1\)
Simplify: \(\dfrac{x^2−3x−10}{x^2+x−2}\).
- Answer
-
\(\dfrac{x−5}{x−1},x\neq −2,x\neq 1\)
We now summarize the steps you should follow to simplify rational expressions.
- Factor the numerator and denominator completely.
- Simplify by dividing out common factors.
Usually, we leave the simplified rational expression in factored form. This way, it is easy to check that we have removed all the common factors.
We’ll use the methods we have learned to factor the polynomials in the numerators and denominators in the following examples.
Every time we write a rational expression, we should make a statement disallowing values that would make a denominator zero. However, to let us focus on the work at hand, we will omit writing it in the examples.
Simplify: \(\dfrac{3a^2−12ab+12b^2}{6a^2−24b^2}\).
Solution
\(\begin{array} {ll} &\dfrac{3a^2−12ab+12b^2}{6a^2−24b^2} \\ & \\ & \\ \begin{array} {l} \text{Factor the numerator and denominator,} \\ \text{first factoring out the GCF.} \end{array} &\dfrac{3(a^2−4ab+4b^2)}{6(a^2−4b^2)} \\ & \\ &\dfrac{3(a−2b)(a−2b)}{6(a+2b)(a−2b)} \\ & \\ \text{Remove the common factors of }a−2b\text{ and }3. &\dfrac{\cancel{3}(a−2b)\cancel{(a−2b)}}{\cancel{3}·2(a+2b)\cancel{(a−2b)}} \\ &\dfrac{a−2b}{2(a+2b)} \end{array} \)
Simplify: \(\dfrac{2x^2−12xy+18y^2}{3x^2−27y^2}\).
- Answer
-
\(\dfrac{2(x−3y)}{3(x+3y)}\)
Simplify: \(\dfrac{5x^2−30xy+25y^2}{2x^2−50y^2}\).
- Answer
-
\(\dfrac{5(x−y)}{2(x+5y)}\)
Now we will see how to simplify a rational expression whose numerator and denominator have opposite factors. We previously introduced opposite notation: the opposite of \(a\) is \(−a\) and \(−a=−1·a\).
The numerical fraction, say \(\dfrac{7}{−7}\) simplifies to \(−1\). We also recognize that the numerator and denominator are opposites.
The fraction \(\dfrac{a}{−a}\), whose numerator and denominator are opposites also simplifies to \(−1\).
\[\begin{array} {ll} \text{Let’s look at the expression }b−a. &b−a \\ \text{Rewrite.} &−a+b \\ \text{Factor out }–1. &−1(a−b) \nonumber\end{array} \]
This tells us that \(b−a\) is the opposite of \(a−b\).
In general, we could write the opposite of \(a−b\) as \(b−a\). So the rational expression \(\dfrac{a−b}{b−a}\) simplifies to \(−1\).
The opposite of \(a−b\) is \(b−a\).
\[\dfrac{a−b}{b−a}=−1 \quad a\neq b\nonumber\]
An expression and its opposite divide to \(−1\).
We will use this property to simplify rational expressions that contain opposites in their numerators and denominators. Be careful not to treat \(a+b\) and \(b+a\) as opposites. Recall that in addition, order doesn’t matter so \(a+b=b+a\). So if \(a\neq −b\), then \(\dfrac{a+b}{b+a}=1\).
Simplify: \(\dfrac{x^2−4x−32}{64−x^2}\)
Solution
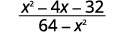 |
|
| Factor the numerator and the denominator. | 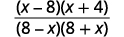 |
| Recognize the factors that are opposites. | 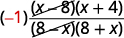 |
| Simplify. | 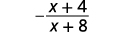 |
Simplify: \(\dfrac{x^2−4x−5}{25−x^2}\)
- Answer
-
\(−\dfrac{x+1}{x+5}\)
Simplify: \(\dfrac{x^2+x−2}{1−x^2}\).
- Answer
-
\(−\dfrac{x+2}{x+1}\)
Multiply Rational Expressions
To multiply rational expressions, we do just what we did with numerical fractions. We multiply the numerators and multiply the denominators. Then, if there are any common factors, we remove them to simplify the result.
If \(p\), \(q\), \(r\), and \(s\) are polynomials where \(q\neq 0\), \(s\neq 0\), then
\[\dfrac{p}{q}·\dfrac{r}{s}=\dfrac{pr}{qs}\nonumber\]
To multiply rational expressions, multiply the numerators and multiply the denominators.
Remember, throughout this chapter, we will assume that all numerical values that would make the denominator be zero are excluded. We will not write the restrictions for each rational expression, but keep in mind that the denominator can never be zero. So in this next example, \(x\neq 0\), \(x\neq 3\), and \(x\neq 4.\)
Simplify: \(\dfrac{2x}{x^2−7x+12}·\dfrac{x^2−9}{6x^2}\).
Solution
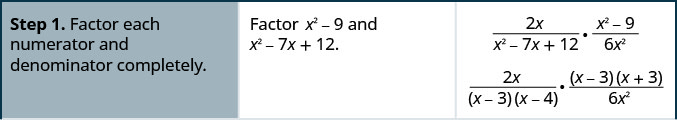


Simplify: \(\dfrac{5x}{x^2+5x+6}·\dfrac{x^2−4}{10x}\).
- Answer
-
\(\dfrac{x−2}{2(x+3)}\)
Simplify: \(\dfrac{9x^2}{x^2+11x+30}·\dfrac{x^2−36}{3x^2}\).
- Answer
-
\(\dfrac{3(x−6)}{x+5}\)
- Factor each numerator and denominator completely.
- Multiply the numerators and denominators.
- Simplify by dividing out common factors.
Multiply: \(\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5}\).
Solution
\(\begin{array} {ll} &\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5} \\ & \\ \begin{array} {ll} \text{Factor the numerators and denominators} \\ \text{and then multiply.} \end{array} &\dfrac{(3a+1)(a−3)(a+5)(a+5)}{(a−5)(a+5)(3a+1)(a−5)} \\ & \\ \begin{array} {l} \text{Simplify by dividing out} \\ \text{common factors.} \end{array} &\dfrac{\cancel{(3a+1)}(a−3)\cancel{(a+5)}(a+5)}{(a−5)\cancel{(a+5)}\cancel{(3a+1)}(a−5)} \\ & \\ \text{Simplify.} &\dfrac{(a−3)(a+5)}{(a−5)(a−5)} \\ & \\ \text{Rewrite }(a−5)(a−5)\text{ using an exponent.} &\dfrac{(a−3)(a+5)}{(a−5)^2} \end{array}\)
Simplify: \(\dfrac{2x^2+5x−12}{x^2−16}·\dfrac{x^2−8x+16}{2x^2−13x+15}\).
- Answer
-
\(\dfrac{x−4}{x−5}\)
Simplify: \(\dfrac{4b^2+7b−2}{1−b^2}·\dfrac{b^2−2b+1}{4b^2+15b−4}\).
- Answer
-
\(−\dfrac{(b+2)(b−1)}{(1+b)(b+4)}\)
Divide Rational Expressions
Just like we did for numerical fractions, to divide rational expressions, we multiply the first fraction by the reciprocal of the second.
If \(p\), \(q\), \(r\), and \(s\) are polynomials where \(q\neq 0\), \(r\neq 0\), \(s\neq 0\), then
\[\dfrac{p}{q}÷\dfrac{r}{s}=\dfrac{p}{q}·\dfrac{s}{r}\nonumber\]
To divide rational expressions, multiply the first fraction by the reciprocal of the second.
Once we rewrite the division as multiplication of the first expression by the reciprocal of the second, we then factor everything and look for common factors.
Divide: \(\dfrac{p^3+q^3}{2p^2+2pq+2q^2}÷\dfrac{p^2−q^2}{6}\).
Solution




Simplify: \(\dfrac{x^3−8}{3x^2−6x+12}÷\dfrac{x^2-4}{6}\).
- Answer
-
\(\dfrac{2(x^2+2x+4)}{(x+2)(x^2−2x+4)}\)
Simplify: \(\dfrac{2z^2}{z^2−1}÷\dfrac{z^3−z^2+z}{z^3+1}\).
- Answer
-
\(\dfrac{2z}{z−1}\)
- Rewrite the division as the product of the first rational expression and the reciprocal of the second.
- Factor the numerators and denominators completely.
- Multiply the numerators and denominators together.
- Simplify by dividing out common factors.
Recall from Use the Language of Algebra that a complex fraction is a fraction that contains a fraction in the numerator, the denominator or both. Also, remember a fraction bar means division. A complex fraction is another way of writing division of two fractions.
Divide: \(\dfrac{\dfrac{6x^2−7x+2}{4x−8}}{\dfrac{2x^2−7x+3}{x^2−5x+6}}\).
Solution
\(\begin{array} {ll} &\dfrac{\dfrac{6x^2−7x+2}{4x−8}}{\dfrac{2x^2−7x+3}{x^2−5x+6}} \\ & \\ \text{Rewrite with a division sign.} &\dfrac{6x^2−7x+2}{4x−8}÷\dfrac{2x^2−7x+3}{x^2−5x+6} \\ & \\ \begin{array} {l} \text{Rewrite as product of first times reciprocal} \\ \text{of second.} \end{array} &\dfrac{6x^2−7x+2}{4x−8}·\dfrac{x^2−5x+6}{2x^2−7x+3} \\ & \\ \begin{array} {l} \text{Factor the numerators and the} \\ \text{denominators, and then multiply.} \end{array} &\dfrac{(2x−1)(3x−2)(x−2)(x−3)}{4(x−2)(2x−1)(x−3)} \\ & \\ \text{Simplify by dividing out common factors.} &\dfrac{\cancel{(2x−1)}(3x−2)\cancel{(x−2)}\cancel{(x−3)}}{4\cancel{(x−2)}\cancel{(2x−1)}\cancel{(x−3)}} \\ \text{Simplify.} &\dfrac{3x−2}{4} \end{array}\)
Simplify: \(\dfrac{\dfrac{3x^2+7x+2}{4x+24}}{\dfrac{3x^2−14x−5}{x^2+x−30}}\).
- Answer
-
\(\dfrac{x+2}{4}\)
Simplify: \(\dfrac{\dfrac{y^2−36}{2y^2+11y−6}}{\dfrac{2y^2−2y−60}{8y−4}}\).
- Answer
-
\(\dfrac{2}{y+5}\)
If we have more than two rational expressions to work with, we still follow the same procedure. The first step will be to rewrite any division as multiplication by the reciprocal. Then, we factor and multiply.
Perform the indicated operations: \(\dfrac{3x−6}{4x−4}·\dfrac{x^2+2x−3}{x^2−3x−10}÷\dfrac{2x+12}{8x+16}\).
Solution
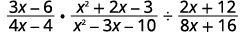 |
|
| Rewrite the division as multiplication by the reciprocal. |
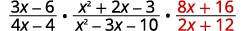 |
| Factor the numerators and the denominators. | 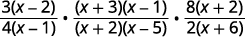 |
| Multiply the fractions. Bringing the constants to the front will help when removing common factors. |
|
| Simplify by dividing out common factors. | 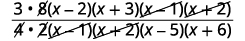 |
| Simplify. | 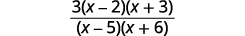 |
Perform the indicated operations: \(\dfrac{4m+4}{3m−15}·\dfrac{m^2−3m−10}{m^2−4m−32}÷\dfrac{12m−36}{6m−48}\).
- Answer
-
\(\dfrac{2(m+1)(m+2)}{3(m+4)(m−3)}\)
Perform the indicated operations: \(\dfrac{2n^2+10n}{n−1}÷\dfrac{n^2+10n+24}{n^2+8n−9}·\dfrac{n+4}{8n^2+12n}\).
- Answer
-
\(\dfrac{(n+5)(n+9)}{2(n+6)(2n+3)}\)
Multiply and Divide Rational Functions
We started this section stating that a rational expression is an expression of the form \(\dfrac{p}{q}\), where p and q are polynomials and \(q\neq 0\). Similarly, we define a rational function as a function of the form \(R(x)=\dfrac{p(x)}{q(x)}\) where \(p(x)\) and \(q(x)\) are polynomial functions and \(q(x)\) is not zero.
A rational function is a function of the form
\[R(x)=\dfrac{p(x)}{q(x)}\nonumber\]
where \(p(x)\) and \(q(x)\) are polynomial functions and \(q(x)\) is not zero.
The domain of a rational function is all real numbers except for those values that would cause division by zero. We must eliminate any values that make \(q(x)=0\).
- Set the denominator equal to zero.
- Solve the equation.
- The domain is all real numbers excluding the values found in Step 2.
Find the domain of \(R(x)=\dfrac{2x^2−14x}{4x^2−16x−48}\).
Solution
The domain will be all real numbers except those values that make the denominator zero. We will set the denominator equal to zero , solve that equation, and then exclude those values from the domain.
\(\begin{array} {ll} \text{Set the denominator to zero.} &4x^2−16x−48=0 \\ \text{Factor, first factor out the GCF.} &4(x^2−4x−12)=0 \\ &4(x−6)(x+2)=0 \\ \text{Use the Zero Product Property.} &4\neq 0\quad x−6=0\quad x+2=0 \\ \text{Solve.} &\hspace{24mm}x=6\qquad x=−2 \\ &\text{The domain of }R(x)\text{ is all real numbers} \\ &\text{where }x\neq 6\text{ and }x\neq −2 \end{array}\).
Find the domain of \(R(x)=\dfrac{2x^2−10x}{4x^2−16x−20}\).
- Answer
-
The domain of \(R(x)\) is all real numbers where \(x\neq 5\) and \(x\neq −1\).
Find the domain of \(R(x)=\dfrac{4x^2−16x}{8x^2−16x−64}\).
- Answer
-
The domain of \(R(x)\) is all real numbers where \(x\neq 4\) and \(x\neq −2\).
To multiply rational functions, we multiply the resulting rational expressions on the right side of the equation using the same techniques we used to multiply rational expressions.
Find \(R(x)=f(x)·g(x)\) where \(f(x)=\dfrac{2x−6}{x^2−8x+15}\) and \(g(x)=\dfrac{x^2−25}{2x+10}\).
Solution
\(\begin{array} {ll} &R(x)=f(x)·g(x) \\ & \\ &R(x)=\dfrac{2x−6}{x^2−8x+15}·\dfrac{x^2−25}{2x+10} \\ & \\ \text{Factor each numerator and denominator.} &R(x)=\dfrac{2(x−3)}{(x−3)(x−5)}·\dfrac{(x−5)(x+5)}{2(x+5)} \\ & \\ \text{Multiply the numerators and denominators.} &R(x)=\dfrac{2(x−3)(x−5)(x+5)}{2(x−3)(x−5)(x+5)} \\ & \\ \text{Remove common factors.} &R(x)=\dfrac{\cancel{2}\cancel{(x−3)}\cancel{(x−5)}\cancel{(x+5)}}{\cancel{2}\cancel{(x−3)}\cancel{(x−5)}\cancel{(x+5)}} \\ & \\ \text{Simplify.} &R(x)=1 \end{array}\)
Find \(R(x)=f(x)·g(x)\) where \(f(x)=\dfrac{3x−21}{x^2−9x+14}\) and \(g(x)=\dfrac{2x^2−8}{3x+6}\).
- Answer
-
\(R(x)=2\)
Find \(R(x)=f(x)·g(x)\) where \(f(x)=\dfrac{x^2−x}{3x^2+27x−30}\) and \(g(x)=\dfrac{x^2−100}{x^2−10x}\).
- Answer
-
\(R(x)=\dfrac{1}{3}\)
To divide rational functions, we divide the resulting rational expressions on the right side of the equation using the same techniques we used to divide rational expressions.
Find \(R(x)=\dfrac{f(x)}{g(x)}\) where \(f(x)=\dfrac{3x^2}{x^2−4x}\) and \(g(x)=\dfrac{9x^2−45x}{x^2−7x+10}\).
Solution
\(\begin{array} {ll} &R(x)=\dfrac{f(x)}{g(x)} \\ \text{Substitute in the functions }f(x),\space g(x). &R(x)=\dfrac{\dfrac{3x^2}{x^2−4x}}{\dfrac{9x^2−45x}{x^2−7x+10}} \\ & \\ \begin{array} {l} \text{Rewrite the division as the product of} \\ f(x)\text{ and the reciprocal of }g(x). \end{array} &R(x)=\dfrac{3x^2}{x^2−4x}·\dfrac{x^2−7x+10}{9x^2−45x} \\ & \\ \begin{array} {l} \text{Factor the numerators and denominators} \\ \text{and then multiply.} \end{array} &R(x)=\dfrac{3·x·x·(x−5)(x−2)}{x(x−4)·3·3·x·(x−5)} \\ & \\ \text{Simplify by dividing out common factors.} &R(x)=\dfrac{\cancel{3}·\cancel{x}·\cancel{x}\cancel{(x−5)}(x−2)}{\cancel{x}(x−4)·\cancel{3}·3·\cancel{x}\cancel{(x−5)}} \\ & \\ &R(x)=\dfrac{x−2}{3(x−4)} \end{array}\)
Find \(R(x)=\dfrac{f(x)}{g(x)}\) where \(f(x)=\dfrac{2x^2}{x^2−8x}\) and \(g(x)=\dfrac{8x^2+24x}{x^2+x−6}\).
- Answer
-
\(R(x)=\dfrac{x−2}{4(x−8)}\)
Find \(R(x)=\dfrac{f(x)}{g(x)}\) where \(f(x)=\dfrac{15x^2}{3x^2+33x}\) and \(g(x)=\dfrac{5x−5}{x^2+9x−22}\).
- Answer
-
\(R(x)=\dfrac{x(x−2)}{x−1}\)
Key Concepts
- Determine the values for which a rational expression is undefined.
- Set the denominator equal to zero.
- Solve the equation.
- Equivalent Fractions Property
If \(a\), \(b\), and \(c\) are numbers where \(b\neq 0\), \(c\neq 0\), then
\(\quad\dfrac{a}{b}=\dfrac{a·c}{b·c}\) and \(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\) - How to simplify a rational expression.
- Factor the numerator and denominator completely.
- Simplify by dividing out common factors.
- Opposites in a Rational Expression
The opposite of \(a−b\) is \(b−a\).
\(\quad\dfrac{a−b}{b−a}=−1 \qquad a\neq b\)
An expression and its opposite divide to \(−1\). - Multiplication of Rational Expressions
If \(p\), \(q\), \(r\), and \(s\) are polynomials where \(q\neq 0\), \(s\neq 0\), then
\(\quad\dfrac{p}{q}·\dfrac{r}{s}=\dfrac{pr}{qs}\) - How to multiply rational expressions.
- Factor each numerator and denominator completely.
- Multiply the numerators and denominators.
- Simplify by dividing out common factors.
- Division of Rational Expressions
If \(p\), \(q\), \(r\), and \(s\) are polynomials where \(q\neq 0\), \(r\neq 0\), \(s\neq 0\), then
\(\quad\dfrac{p}{q}÷\dfrac{r}{s}=\dfrac{p}{q}·\dfrac{s}{r}\) - How to divide rational expressions.
- Rewrite the division as the product of the first rational expression and the reciprocal of the second.
- Factor the numerators and denominators completely.
- Multiply the numerators and denominators together.
- Simplify by dividing out common factors.
- How to determine the domain of a rational function.
- Set the denominator equal to zero.
- Solve the equation.
- The domain is all real numbers excluding the values found in Step 2.
Glossary
- rational expression
- A rational expression is an expression of the form \(\dfrac{p}{q}\), where \(p\) and \(q\) are polynomials and \(q\neq 0\).
- simplified rational expression
- A simplified rational expression has no common factors, other than \(1\), in its numerator and denominator.
- rational function
- A rational function is a function of the form \(R(x)=\dfrac{p(x)}{q(x)}\) where \(p(x)\) and \(q(x)\) are polynomial functions and \(q(x)\) is not zero.


