Chapter 8 Review Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Chapter Review Exercises
Simplify Expressions with Roots
In the following exercises, simplify.
-
- √225
- −√16
-
- −√169
- √−8
-
- 3√8
- 4√81
- 5√243
-
- 3√−512
- 4√−81
- 5√−1
- Answer
-
1.
- 15
- −4
3.
- 2
- 3
- 3
In the following exercises, estimate each root between two consecutive whole numbers.
-
- √68
- 3√84
- Answer
-
1.
- 8<√68<9
- 4<3√84<5
In the following exercises, approximate each root and round to two decimal places.
-
- √37
- 3√84
- 4√125
- Answer
-
1. Solve for yourself
In the following exercises, simplify using absolute values as necessary.
-
- 3√a3
- 7√b7
-
- √a14
- √w24
-
- 4√m8
- 5√n20
-
- √121m20
- −√64a2
-
- 3√216a6
- 5√32b20
-
- √144x2y2
- √169w8y10
- 3√8a51b6
- Answer
-
1.
- a
- |b|
3.
- m2
- n4
5.
- 6a2
- 2b4
Simplify Radical Expressions
In the following exercises, use the Product Property to simplify radical expressions.
- √125
- √675
-
- 3√625
- 6√128
- Answer
-
1. 5√5
3.
- 53√5
- 26√2
In the following exercises, simplify using absolute value signs as needed.
-
- √a23
- 3√b8
- 8√c13
-
- √80s15
- 5√96a7
- 6√128b7
-
- √96r3s3
- 3√80x7y6
- 4√80x8y9
-
- 5√−32
- 8√−1
-
- 8+√96
- 2+√402
- Answer
-
2.
- 4|s7|√5s
- 2a5√3a2
- 2|b|6√2b
4.
- −2
- not real
In the following exercises, use the Quotient Property to simplify square roots.
-
- √7298
- 3√2481
- 4√696
-
- √y4y8
- 5√u21u11
- 6√v30v12
- √300m564
-
- √28p7q2
- 3√81s8t3
- 4√64p15q12
-
- √27p2q108p4q3
- 3√16c5d7250c2d2
- 6√2m9n7128m3n
-
- √80q5√5q
- 3√−6253√5
- 4√80m74√5m
- Answer
-
1.
- 67
- 23
- 12
3. 10m2√3m8
5.
- 12|pq|
- 2cd5√2d25
- |mn|6√22
Simplify Rational Exponents
In the following exercises, write as a radical expression.
-
- r12
- s13
- t14
- Answer
-
1.
- √r
- 3√s
- 4√t
In the following exercises, write with a rational exponent.
-
- √21p
- 4√8q
- 46√36r
- Answer
-
1. Solve for yourself
In the following exercises, simplify.
-
- 62514
- 24315
- 3215
-
- (−1,000)13
- −1,00013
- (1,000)−13
-
- (−32)15
- (243)−15
- −12513
- Answer
-
1.
- 5
- 3
- 2
3.
- −2
- 13
- −5
In the following exercises, write with a rational exponent.
-
- 4√r7
- (5√2pq)3
- 4√(12m7n)3
- Answer
-
1. Solve for yourself
In the following exercises, simplify.
-
- 2532
- 9−32
- (−64)23
-
- −6432
- −64−32
- (−64)32
- Answer
-
1.
- 125
- 127
- 16
In the following exercises, simplify.
-
- 652⋅612
- (b15)35
- w27w97
-
- a34⋅a−14a−104
- (27b23c−52b−73c12)13
- Answer
-
1.
- 63
- b9
- 1w
Add, Subtract and Multiply Radical Expressions
In the following exercises, simplify.
-
- 7√2−3√2
- 73√p+23√p
- 53√x−33√x
-
- √11b−5√11b+3√11b
- 84√11cd+54√11cd−94√11cd
-
- √48+√27
- 3√54+3√128
- 64√5−324√320
-
- √80c7−√20c7
- 24√162r10+44√32r10
- 3√75y2+8y√48−√300y2
- Answer
-
1.
- 4√2
- 93√p
- 23√x
3.
- 7√3
- 73√2
- 34√5
5. 37y√3
In the following exercises, simplify.
-
- (5√6)(−√12)
- (−24√18)(−4√9)
-
- (3√2x3)(7√18x2)
- (−63√20a2)(−23√16a3)
- Answer
-
2.
- 126x2√2
- 48a3√a2
In the following exercises, multiply.
-
- √11(8+4√11)
- 3√3(3√9+3√18)
-
- (3−2√7)(5−4√7)
- (3√x−5)(3√x−3)
- (2√7−5√11)(4√7+9√11)
-
- (4+√11)2
- (3−2√5)2
- (7+√10)(7−√10)
- (3√3x+2)(3√3x−2)
- Answer
-
2.
- 71−22√7
- 3√x2−83√x+15
4.
- 27+8√11
- 29−12√5
6. 3√9x2−4
Divide Radical Expressions
In the following exercises, simplify.
-
- √48√75
- 3√813√24
-
- √320mn−5√45m−7n3
- 3√16x4y−23√−54x−2y4
- Answer
-
2.
- 8m43n4
- −x22y2
In the following exercises, rationalize the denominator.
-
- 8√3
- √740
- 8√2y
-
- 13√11
- 3√754
- 33√3x2
-
- 14√4
- 4√932
- 64√9x3
- Answer
-
2.
- 3√12111
- 3√286
- 3√9xx
In the following exercises, simplify.
- 72−√6
- √5√n−√7
- √x+√8√x−√8
- Answer
-
1. −7(2+√6)2
3. (√x+2√2)2x−8
Solve Radical Equations
In the following exercises, solve.
- √4x−3=7
- √5x+1=−3
- 3√4x−1=3
- √u−3+3=u
- 3√4x+5−2=−5
- (8x+5)13+2=−1
- √y+4−y+2=0
- 2√8r+1−8=2
- Answer
-
2. no solution
4. u=3,u=4
6. x=−4
8. r=3
In the following exercises, solve.
- √10+2c=√4c+16
- 3√2x2+9x−18=3√x2+3x−2
- √r+6=√r+8
- √x+1−√x−2=1
- Answer
-
2. x=−8,x=2
4. x=3
In the following exercises, solve. Round approximations to one decimal place.
- Landscaping Reed wants to have a square garden plot in his backyard. He has enough compost to cover an area of 75 square feet. Use the formula s=√A to find the length of each side of his garden. Round your answers to th nearest tenth of a foot.
- Accident investigation An accident investigator measured the skid marks of one of the vehicles involved in an accident. The length of the skid marks was 175 feet. Use the formula s=√24d to find the speed of the vehicle before the brakes were applied. Round your answer to the nearest tenth.
- Answer
-
2. 64.8 feet
Use Radicals in Functions
In the following exercises, evaluate each function.
- g(x)=√6x+1, find
- g(4)
- g(8)
- G(x)=√5x−1, find
- G(5)
- G(2)
- h(x)=3√x2−4, find
- h(−2)
- h(6)
- For the function g(x)=4√4−4x, find
- g(1)
- g(−3)
- Answer
-
2.
- G(5)=2√6
- G(2)=3
4.
- g(1)=0
- g(−3)=2
In the following exercises, find the domain of the function and write the domain in interval notation.
- g(x)=√2−3x
- F(x)=√x+3x−2
- f(x)=3√4x2−16
- F(x)=4√10−7x
- Answer
-
2. (2,∞)
4. [710,∞)
In the following exercises,
- find the domain of the function
- graph the function
- use the graph to determine the range
- g(x)=√x+4
- g(x)=2√x
- f(x)=3√x−1
- f(x)=3√x+3
- Answer
-
2.
- domain: [0,∞)
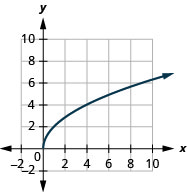
Figure 8.E.1- range: [0,∞)
4.
- domain: (−∞,∞)
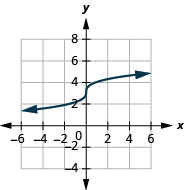
Figure 8.E.2- range: (−∞,∞)
Use the Complex Number System
In the following exercises, write each expression in terms of i and simplify if possible.
-
- √−100
- √−13
- √−45
- Answer
-
Solve for yourself
In the following exercises, add or subtract.
- √−50+√−18
- (8−i)+(6+3i)
- (6+i)−(−2−4i)
- (−7−√−50)−(−32−√−18)
- Answer
-
1. 8√2i
3. 8+5i
In the following exercises, multiply.
- (−2−5i)(−4+3i)
- −6i(−3−2i)
- √−4⋅√−16
- (5−√−12)(−3+√−75)
- Answer
-
1. 23+14i
3. −6
In the following exercises, multiply using the Product of Binomial Squares Pattern.
- (−2−3i)2
- Answer
-
1. −5−12i
In the following exercises, multiply using the Product of Complex Conjugates Pattern.
- (9−2i)(9+2i)
- Answer
-
Solve for yourself
In the following exercises, divide.
- 2+i3−4i
- −43−2i
- Answer
-
1. 225+1125i
In the following exercises, simplify.
- i48
- i255
- Answer
-
1. 1
Practice Test
In the following exercises, simplify using absolute values as necessary.
- 3√125x9
- √169x8y6
- 3√72x8y4
- √45x3y4180x5y2
- Answer
-
1. 5x3
3. 2x2y3√9x2y
In the following exercises, simplify. Assume all variables are positive.
-
- 216−14
- −4932
- √−45
- x−14⋅x54x−34
- (8x23y−52x−73y12)13
- √48x5−√75x5
- √27x2−4x√12+√108x2
- 2√12x5⋅3√6x3
- 3√4(3√16−3√6)
- (4−3√3)(5+2√3)
- 3√1283√54
- √245xy−4√45x4y3
- 13√5
- 32+√3
- √−4⋅√−9
- −4i(−2−3i)
- 4+i3−2i
- i172
- Answer
-
1.
- 14
- −343
3. x74
5. −x2√3x
7. 36x4√2
9. 2−7√3
11. 7x53y7
13. 3(2−√3)
15. −12+8i
17. −i
In the following exercises, solve.
- √2x+5+8=6
- √x+5+1=x
- 3√2x2−6x−23=3√x2−3x+5
- Answer
-
2. x=4
In the following exercise,
- find the domain of the function
- graph the function
- use the graph to determine the range
- g(x)=√x+2
- Answer
-
1.
- domain: [−2,∞)
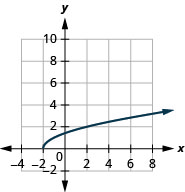
Figure 8.E.3- range: [0,∞)


