Skip to main content
Mathematics LibreTexts

9.3E: Exercises

  1. Last updated
  2. Save as PDF
  • Page ID
    30562

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Practice Makes Perfect

    ExerciseS 1 - 4: Complete the Square of a Binomial Expression

    In the following exercises, complete the square to make a perfect square trinomial. Then write the result as a binomial squared.

      1. \(m^{2}-24 m\)
      2. \(x^{2}-11 x\)
      3. \(p^{2}-\frac{1}{3} p\)
      1. \(n^{2}-16 n\)
      2. \(y^{2}+15 y\)
      3. \(q^{2}+\frac{3}{4} q\)
      1. \(p^{2}-22 p\)
      2. \(y^{2}+5 y\)
      3. \(m^{2}+\frac{2}{5} m\)
      1. \(q^{2}-6 q\)
      2. \(x^{2}-7 x\)
      3. \(n^{2}-\frac{2}{3} n\)
    Answer

    1. a. \((m-12)^{2}\) b. \(\left(x-\frac{11}{2}\right)^{2}\) c. \(\left(p-\frac{1}{6}\right)^{2}\)

    3. a. \((p-11)^{2}\) b. \(\left(y+\frac{5}{2}\right)^{2}\) c. \(\left(m+\frac{1}{5}\right)^{2}\)

    ExerciseS 5 - 28: Solve Quadratic Equations of the Form \(x^{2}+b x+c=0\) by Completing the Square

    In the following exercises, solve by completing the square.

    5. \(u^{2}+2 u=3\)

    6. \(z^{2}+12 z=-11\)

    7. \(x^{2}-20 x=21\)

    8. \(y^{2}-2 y=8\)

    9. \(m^{2}+4 m=-44\)

    10. \(n^{2}-2 n=-3\)

    11. \(r^{2}+6 r=-11\)

    12. \(t^{2}-14 t=-50\)

    13. \(a^{2}-10 a=-5\)

    14. \(b^{2}+6 b=41\)

    15. \(x^{2}+5 x=2\)

    16. \(y^{2}-3 y=2\)

    17. \(u^{2}-14 u+12=-1\)

    18. \(z^{2}+2 z-5=2\)

    19. \(r^{2}-4 r-3=9\)

    20. \(t^{2}-10 t-6=5\)

    21. \(v^{2}=9 v+2\)

    22. \(w^{2}=5 w-1\)

    23. \(x^{2}-5=10 x\)

    24. \(y^{2}-14=6 y\)

    25. \((x+6)(x-2)=9\)

    26. \((y+9)(y+7)=80\)

    27. \((x+2)(x+4)=3\)

    28. \((x-2)(x-6)=5\)

    Answer

    5. \(u=-3, u=1\)

    7. \(x=-1, x=21\)

    9. \(m=-2 \pm 2 \sqrt{10} i\)

    11. \(r=-3 \pm \sqrt{2} i\)

    13. \(a=5 \pm 2 \sqrt{5}\)

    15. \(x=-\frac{5}{2} \pm \frac{\sqrt{33}}{2}\)

    17. \(u=1, u=13\)

    19. \(r=-2, r=6\)

    21. \(v=\frac{9}{2} \pm \frac{\sqrt{89}}{2}\)

    23. \(x=5 \pm \sqrt{30}\)

    25. \(x=-7, x=3\)

    27. \(x=-5, x=-1\)

    ExerciseS 29 - 40: Solve Quadratic Equations of the Form \(a x^{2}+b x+c=0\) by Completing the Square

    In the following exercises, solve by completing the square.

    29. \(3 m^{2}+30 m-27=6\)

    30. \(2 x^{2}-14 x+12=0\)

    31. \(2 n^{2}+4 n=26\)

    32. \(5 x^{2}+20 x=15\)

    33. \(2 c^{2}+c=6\)

    34. \(3 d^{2}-4 d=15\)

    35. \(2 x^{2}+7 x-15=0\)

    36. \(3 x^{2}-14 x+8=0\)

    37. \(2 p^{2}+7 p=14\)

    38. \(3 q^{2}-5 q=9\)

    39. \(5 x^{2}-3 x=-10\)

    40. \(7 x^{2}+4 x=-3\)

    Answer

    29. \(m=-11, m=1\)

    31. \(n=1 \pm \sqrt{14}\)

    33. \(c=-2, c=\frac{3}{2}\)

    35. \(x=-5, x=\frac{3}{2}\)

    37. \(p=-\frac{7}{4} \pm \frac{\sqrt{161}}{4}\)

    39. \(x=\frac{3}{10} \pm \frac{\sqrt{191}}{10} i\)

    ExerciseS 41 - 42: writing exercises

    41. Solve the equation \(x^{2}+10 x=-25\)

    1. by using the Square Root Property
    2. by Completing the Square
    3. Which method do you prefer? Why?

    42. Solve the equation \(y^{2}+8y=48\) by completing the square and explain all your steps.

    Answer

    41. Answers will vary

    Self Check

    a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

    This table provides a checklist to evaluate mastery of the objectives of this section. Choose how would you respond to the statement “I can complete the square of a binomial expression.” “Confidently,” “with some help,” or “No, I don’t get it.” Choose how would you respond to the statement “I can solve quadratic equations of the form x squared plus b times x plus c equals 0 by completing the square.” “Confidently,” “with some help,” or “No, I don’t get it.” Choose how would you respond to the statement “I can solve quadratic equations of the form a times x squared plus b times x plus c equals 0 by completing the square.” “Confidently,” “with some help,” or “No, I don’t get it.”
    Figure 9.2.103

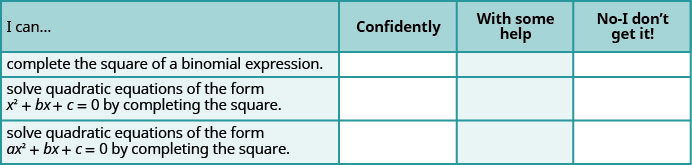
    b. After reviewing this checklist, what will you do to become confident for all objectives?

    This page titled 9.3E: Exercises is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.