6.4: Multiply polynomial expressions
- Page ID
- 45061
We can multiply polynomials of different forms, but the method will be the same. We first look at multiplying monomials, multiplying a monomial and polynomial, and then finish with multiplying polynomials. We are using the product rule of exponents and the distributive property.
Multiply a Polynomial Expression by a Monomial
Multiply: \((4x^3y^4z)(2x^2y^6z^3)\)
Solution
\[\begin{array}{rl}(4x^3y^4z)(2x^2y^6z^3)&\text{Rewrite without parenthesis} \\ 4x^3y^4z\cdot 2x^2y^6z^3&\text{Multiply coefficients and apply the product rule of exponents} \\ 4\cdot 2\cdot x^{3+2}y^{4+6}z^{1+3}&\text{Simplify} \\ 8x^5y^{10}z^4&\text{Product}\end{array}\nonumber\]
Multiply: \(4x^3(5x^2-2x+5)\)
Solution
\[\begin{array}{rl}4x^3(5x^2-2x+5)&\text{Distribute }4x^3 \\ \color{blue}{4x^3}\color{black}{}\cdot 5x^2-\color{blue}{4x^3}\color{black}{}\cdot 2x+\color{blue}{4x^3}\color{black}{}\cdot 5&\text{Multiply and apply the product rule of exponents} \\ 20x^5-8x^4+20x^3&\text{Product}\end{array}\nonumber\]
Multiply: \(2a^3b(3ab^2-4a)\)
Solution
\[\begin{array}{rl}2a^3b(3ab^2-4a)&\text{Distribute }2a^3b \\ \color{blue}{2a^3b}\color{black}{}\cdot 3ab^2-\color{blue}{2a^3b}\color{black}{}\cdot 4a&\text{Multiply and apply the product rule of exponents} \\ 6a^{3+1}b^{1+2}-8a^{3+1}b&\text{Simplify} \\ 6a^4b^3-8a^4b&\text{Product}\end{array}\nonumber\]
Multiplying with Binomials
There are several different methods for multiplying polynomials, all of which result in the same answer. We discuss multiplying by distribution and the FOIL method.
Multiply: \((3x+5)(x+13)\)
Solution
We will multiply using distribution and then simplify.
\[\begin{array}{rl}(3x+5)(x+13)&\text{Distribute }3x\text{ and }5\text{ to }(x+13) \\ \color{blue}{3x}\color{black}{}(x+13)+\color{blue}{5}\color{black}{}(x+13)&\text{Distribute} \\ 3x^2+39x+5x+65&\text{Combine like terms} \\ 3x^2+44x+65&\text{Product}\end{array}\nonumber\]
Multiply: \((4x+7y)(3x-2y)\)
Solution
We will multiply using the FOIL method. FOIL is an acronym and represents
\[\begin{array}{ll}\text{First}&\text{-Multiply the first terms in each parenthesis} \\ \text{Outer}&\text{-Multiply the outer terms in each parenthesis} \\ \text{Inner}&\text{-Multiply the inner terms in each parenthesis} \\ \text{Last}&\text{-Multiply the last terms in each parenthesis}\end{array}\nonumber\]
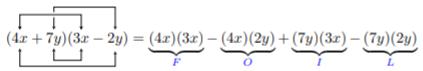
\[\begin{aligned}&=12x^2-8xy+21xy-14y^2 \\ &=12x^2+13xy+14y^2\end{aligned}\]
Multiplying with Trinomials
A trinomial is a polynomial with three terms. Usually, in Algebra, a trinomial takes the form of \(ax^2+bx+c\), where \(a,\: b,\) and \(c\) are coefficients.
Multiply: \((2x-5)(4x^2-7x+3)\)
Solution
Since we are multiplying a binomial with a trinomial, we can use distribution to multiply.
\[\begin{array}{rl}(2x-5)(4x^2-7x+3)&\text{Distribute }2x\text{ and }-5\text{ to }(4x^2-7x+3) \\ \color{blue}{2x}\color{black}{}\cdot (4x^2-7x+3)-\color{blue}{5}\color{black}{}(4x^2-7x+3)&\text{Distribute} \\ 8x^3-14x^2+6x-20x^2+35x-15&\text{Combine like terms} \\ 8x^3-34x^2+41x-15&\text{Product}\end{array}\nonumber\]
Multiply: \((5x^2+x-10)(3x^2-10x-6)\)
Solution
Since we are multiplying a trinomial with a trinomial, then we can use distribution to multiply.
\[\begin{array}{rl}(5x^2+x-10)(3x^2-10x-6)&\text{Distribute }5x^2,\: x,\text{ and }-10 \\ &\text{to }(3x^2-10x-6) \\ \color{blue}{5x^2}\color{black}{}\cdot (3x^2-10x-6)+\color{blue}{x}\color{black}{}(3x^2-10x-6)-\color{blue}{10}\color{black}{}(3x^2-10x-6)&\text{Distribute} \\ 15x^4-50x^3-30x^2+3x^3-10x^2-6x-30x^2+100x+60&\text{Combine like terms} \\ 15x^4-47x^3-70x^2+94x+60&\text{Product}\end{array}\nonumber\]
Multiplying Monomials and Binomials
Multiply: \(3x(2x-4)(x+5)\)
Solution
We first use FOIL to multiply the binomials and then distribute the \(3x\).
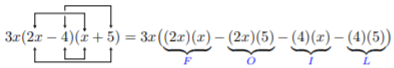
\[\begin{aligned}&=3x(2x^2+10x-4x-20) \\ &=3x(2x^2+6x-20)\end{aligned}\]
Lastly, we distribute \(3x\):
\[\begin{array}{l} 3x(2x^2+6x-20) \\ \color{blue}{3x}\color{black}{}\cdot 2x^2+\color{blue}{3x}\color{black}{}\cdot 6x-\color{blue}{3x}\color{black}{}\cdot 20 \\ 6x^3+18x^2-60x\end{array}\nonumber\]
Thus, the product is \(6x^3+18x^2-60x\).
In Example 6.4.8 , a common error is distributing the \(3x\) first and into both parenthesis. While we can distribute the \(3x\) into the \((2x − 4)\) factor, we cannot distribute into both factors. We recommend to multiply the binomials first, then distribute the monomial last.
Multiplying Polynomial Functions
We can multiply two polynomial functions the same way we multiply polynomial expressions, except, now, we have functions. The method is the same, but the notation and problems change.
If \(f\) and \(g\) are two functions of \(x\), then \[(f\cdot g)(x)=f(x)\cdot g(x)\nonumber\] where \(x\) is in the domain of \(f\) and \(g\).
Let \(f(x)=2x-1\) and \(g(x)=x+4\). Find \((f\cdot g)(x)\).
Solution
We start by applying the definition, then simplify completely.
\[\begin{array}{rl}(f\cdot g)(x)=f(x)\cdot g(x)&\text{Apply the definition} \\ (f\cdot g)(x)=(2x-1)\cdot (x+4)&\text{Multiply two binomials} \\ (f\cdot g)(x)=2x^2+8x-x-4&\text{Combine like terms} \\ (f\cdot g)(x)=2x^2+7x-4&\text{The product of }f\text{ and }g\end{array}\nonumber\]
Multiply Polynomial Expressions Homework
Multiply and simplify.
\(6(p-7)\)
\(2(6x+3)\)
\(5m^4(4m+4)\)
\((4n+6)(8n+8)\)
\((8b+3)(7b-5)\)
\((4x+5)(2x+3)\)
\((3v-4)(5v-2)\)
\((6x-7)(4x+1)\)
\((5x+y)(6x-4y)\)
\((x+3y)(3x+4y)\)
\((7x+5y)(8x+3y)\)
\((r-7)(6r^2-r+5)\)
\((6n-4)(2n^2-2n+5)\)
\((6x+3y)(6x^2-7xy+4y^2)\)
\((8n^2+4n+6)(6n^2-5n+6)\)
\((5k^2+3k+3)(3k^2+3k+6)\)
\(3(3x-4)(2x+1)\)
\(3(2x+1)(4x-5)\)
\(7(x-5)(x-2)\)
\(6(4x-1)(4x+1)\)
\(4k(8k+4)\)
\(3n^2(6n+7)\)
\(3(4r-7)\)
\((2x+1)(x-4)\)
\((r+8)(4r+8)\)
\((7n-6)(n+7)\)
\((6a+4)(a-8)\)
\((5x-6)(4x-1)\)
\((2u+3v)(8u-7v)\)
\((8u+6v)(5u-8v)\)
\((5a+8b)(a-3b)\)
\((4x+8)(4x^2+3x+5)\)
\((2b-3)(4b^2+4b+4)\)
\((3m-2n)(7m^2+6mn+4n^2)\)
\((2a^2+6a+3)(7a^2-6a+1)\)
\((7u^2+8uv-6v^2)(6u^2+4uv+3v^2)\)
\(5(x-4)(2x-3)\)
\(2x(4x+1)(2x-6)\)
\(5x(2x-1)(4x+1)\)
\(3x^2(2x+3)(6x+9)\)
Perform the indicated operations given the set of functions.
Let \(g(x)=4x+5\) and \(h(x)=x^2+5x\), find \((g\cdot h)(x)\).
Let \(p(t)=t-4\) and \(r(t)=2t\), find \((p\cdot r)(t)\).
Let \(f(n)=-2n^2-5n\) and \(k(n)=n+5\), find \((f\cdot k)(n)\).