9.2: Rational Inequalities
- Page ID
- 45128
In earlier chapters, we discussed many types of inequalities, and one of the most critical parts of inequalities is we know the solutions are always intervals of numbers. Hence, we now discuss rational inequalities where the solutions are intervals, but we take one critical detail into account. Since rational inequalities and equations contain excluded values, we must take this into consideration when obtaining the solution. In fact, we use the excluded values and \(x\)-intercepts, if any, to determine the intervals in which make the inequality true. Again, with inequalities, we are trying to find intervals of numbers in which the statements is true.
Step 1. Rewrite the inequality so that only zero is on the right side.
Step 2. Determine where the rational expression is undefined or equals zero.
Step 3. Graph the values found in Step 2. on a number line split into intervals.
Step 4. Take a test point within each interval and determine the sign of the result.
Step 5. Determine the solution, where the solution is the interval in which makes the inequality true.
Be careful when determining the intervals. Recall, where the expression is undefined is not included in the interval, i.e., always use parenthesis for the values in which the expression is undefined.
Solve \(\dfrac{x-3}{x+1}>0\).
Solution
Step 1. Rewrite the inequality so that only zero is on the right side.
Since \(\dfrac{x-3}{x+1}>0\) already has zero on the right side, this step is done.
Step 2. Determine where the rational expression is undefined or equals zero.
To obtain where the rational expression equals zero, we set the numerator equal to zero: \[\begin{aligned} x − 3 &= 0\\ x &= 3\end{aligned}\] To obtain where the expression is undefined, we find its excluded value(s) by setting the denominator equal to zero: \[\begin{aligned}x + 1 &= 0\\ x &= −1\end{aligned}\]
Step 3. Graph the values found in Step 2. on a number line into split into intervals.
Label \(-1\) and \(3\) on a blank real number line:
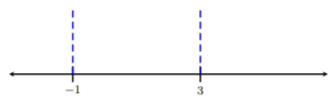
Step 4. Take a test point within each interval and determine the sign of the result.
We take test values on each side of \(−1\) and \(3\). Let’s choose fairly easy numbers such as \(−2,\: 0,\) and \(4\). We plug-n-chug these numbers into \(\dfrac{x − 3}{x + 1}\) and determine whether the value is positive or negative:
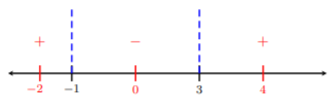
\[\begin{array}{rl} \text{letting }x=-2\Longrightarrow &\dfrac{-2-3}{-2+1}=5>0 \\ \text{letting }x=0\Longrightarrow &\dfrac{0-3}{0+1}=-3<0 \\ \text{letting }x=4\Longrightarrow &\dfrac{4-3}{4+1}=0.2>0\end{array}\nonumber\]
Step 5. Determine the solution, where the solution is the interval in which makes the inequality true.
Since \(\dfrac{x − 3}{x + 1} > 0\) (from Step 1.), then we are looking for where the test values are positive. Looking at the number line above, we see these are the values to the left of \(−1\) and to the right of \(3\). Thus, the solution is \((−∞, −1) ∪ (3, ∞)\).
We always use a parenthesis for the value that is excluded since this value makes the rational expression undefined. Using a bracket or parenthesis for where the expression equals zero is determined by the original inequality sign, e.g., \(<, >\) use parenthesis, and \(≥, ≤\) use brackets.
Solve \(\dfrac{2x+3}{x-2}\leq 1\).
Solution
Step 1. Rewrite the inequality so that only zero is on the right side.
We rewrite \(\dfrac{2x+3}{x-2}\leq 1\) so that there is zero on the right side, and as one fraction: \[\begin{array}{rl}\dfrac{2x+3}{x-2}\leq 1&\text{Subtract }1\text{ from each side} \\ \dfrac{2x+3}{x-2}-1\leq 0&\text{Rewrite as one fraction where LCD: }(x-2) \\ \dfrac{2x+3}{x-2}-\dfrac{x-2}{x-2}\leq 0&\text{Subtract across numerators} \\ \dfrac{2x+3-x+2}{x-2}\leq 0&\text{Simplify} \\ \dfrac{x+5}{x-2}\leq 0&\text{We use this inequality to obtain the solution} \end{array}\nonumber\]
Step 2. Determine where the rational expression is undefined or equals zero.
To obtain where the rational expression equals zero, we set the numerator equal to zero: \[\begin{aligned} x + 5 &= 0\\ x &= −5\end{aligned}\] To obtain the excluded values, we set the denominator equal to zero: \[\begin{aligned}x − 2 &= 0 \\x &= 2\end{aligned}\]
Step 3. Graph the values found in Step 2. on a number line into split into intervals.
Label \(−5\) and \(2\) on a blank number line:
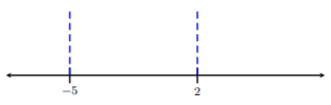
Step 4. Take a test point within each interval and determine the sign of the result.
We take test values on each side of \(−5\) and \(2\). Let’s choose fairly easy numbers such as \(−6,\: 0,\) and \(3\). We plug these numbers into \(\dfrac{x + 5}{x − 2}\) and determine whether the value is positive or negative:
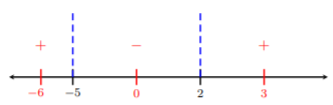
\[\begin{array}{rl} \text{letting }x=-6\Longrightarrow &\dfrac{-6+5}{-6-2}=\dfrac{1}{8}>0 \\ \text{letting }x=0\Longrightarrow &\dfrac{0+5}{0-2}=-\dfrac{5}{2}<0 \\ \text{letting }x=3\Longrightarrow &\dfrac{3+5}{3-2}=8>0\end{array}\nonumber\]
Step 5. Determine the solution, where the solution is the interval in which makes the inequality true.
Since \(\dfrac{x + 5}{x − 2} ≤ 0\) (from Step 1.), then we are looking for where the test values are negative or equal to zero. Looking at the number line above, we see these are the values between \(−5\) and \(2\). Thus, the solution is \([−5, 2)\).
We used a bracket on \(−5\) since the original inequality was \(≤\) and a parenthesis on \(2\) since \(2\) was an excluded value.
Rational Inequalities Homework
Solve the rational inequalities. Write the solution in interval notation.
\(\dfrac{x-3}{x+1}<0\)
\(\dfrac{x-7}{x+6}>0\)
\(\dfrac{x-3}{x+1}<1\)
\(\dfrac{x+27}{x+4}<9\)
\(x+\dfrac{45}{x}<14\)
\(\dfrac{(x-9)(x+9)}{x}\geq 0\)
\(\dfrac{(x+12)(x-4)}{x-1}\geq 0\)
\(\dfrac{3x}{7-x}<x\)
\(\dfrac{4x}{3-x}\geq 4x\)
\(\dfrac{8}{x-3}>\dfrac{6}{x-1}\)
Find the values of \(x\) that satisfy the given condition for the function.
Solve \(R(x)\geq 0\) if \(R(x)=\dfrac{x+6}{x-4}\).
Solve \(R(x)\leq 0\) if \(R(x)=\dfrac{x-4}{x+8}\).


