11.2: Completing the Square
- Page ID
- 45111
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When solving quadratic equations previously (then known as trinomial equations), we factored to solve. However, recall, not all equations are factorable. Consider the equation \(x^2 − 2x − 7 = 0\). This equation isn’t factorable, but there are two solutions to this equation: \(1 + 2\sqrt{2}\) and \(1 − 2\sqrt{2}\). Looking at the form of these solutions, we obtained these types of solutions in the previous section while using the square root property. If we can obtain a perfect square, then we can apply the square root property and solve as usual. This method we use to obtain a perfect square is called completing the square.
Recall. Special product formulas for perfect square trinomials:
\[(a+b)^2=a^2+2ab+b^2\quad\text{or}\quad (a-b)^2=a^2-2ab+b^2\nonumber\]
We use these formulas to help us solve by completing the square.
Complete The Square
We first begin with completing the square and rewriting the trinomial in factored form using the perfect square trinomial formulas.
Complete the square by finding \(c\): \(x^2+8x+c\)
Solution
There are a couple of ways to complete the square. The first way is to mentally think about a number for \(c\) such that we can factor the trinomial as a perfect square trinomial, i.e.,
\[x^2+8x+c=(x+\underline{\quad} )^2\nonumber\]
Some might see that this number \(c = 16\) if they are keen at factoring. Notice, \((x + 4)^2 = x^2 + 8x + 16\). Another way is to, literally, complete the square:
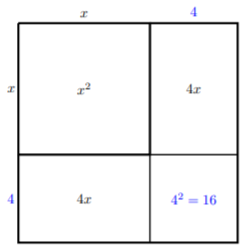
Notice the square has all components of the perfect square trinomial. Hence, we can see the dimensions of this square to be
\[(x+4)\times (x+4)\nonumber\]
which is
\[(x+4)^2\nonumber\]
and the missing constant coefficient is \(16\), the square of \(4\). Using one of these methods will suffice depending on the type of learner. Some students enjoy the geometric relationship between the quadratic equation and the square, and some enjoy the algebraic method. It is up to the discretion of the student.
Thus, we see \(c = 16\) and the perfect square trinomial \(x^2 + 8x + \color{blue}{16}\) is factored into \((x + 4)^2\).
In Example 11.2.1 , notice \(c\) was derived from the middle term \(8x\). Looking at the square, we see the linear term’s coefficient \(8\) was divided in half and squared (because we were finding the area of the bottom right square). This is exactly the method we use for all problems when completing the square.
To complete the square of any trinomial, we always square half of the linear term’s coefficient, i.e.,
\[\left(\dfrac{b}{2}\right)^2\quad\text{or}\quad\left(\dfrac{1}{2}b\right)^2\nonumber\]
We usually use the second expression when the middle term's coefficient is a fraction.
Complete the square by finding \(c\): \(x^2-7x+c\)
Solution
To obtain \(c\), we use the formula above \(\left(\dfrac{b}{2}\right)^2\).
\[\begin{array}{rl} x^2-7x+\color{blue}{c}&\color{black}{b}=-7;\text{ apply formula }\left(\dfrac{b}{2}\right)^2 \\ x^2-7x+\color{blue}{\left(\dfrac{-7}{2}\right)^2}&\color{black}{\text{Simplify }}c\\ x^2-7x+\color{blue}{\dfrac{49}{4}}&\color{black}{\text{Perfect square trinomial}}\end{array}\nonumber\]
Thus, \(c=\dfrac{49}{4}\). Rewriting this perfect square trinomial in factored form, we get
\[x^2-7x+\color{blue}{\dfrac{49}{4}}\color{black}{=}\left(x-\dfrac{7}{2}\right)^2\nonumber\]
Complete the square by finding \(c\): \(x^2+\dfrac{5}{3}x+c\)
Solution
To obtain \(c\), we use the formula above \(\left(\dfrac{1}{2}b\right)^2\) since the linear term’s coefficient is a fraction.
\[\begin{array}{rl} x^2+\dfrac{5}{3}x+\color{blue}{c}&\color{black}{b}=\dfrac{5}{3};\text{ apply formula }\left(\dfrac{1}{2}b\right)^2 \\ x^2+\dfrac{5}{3}x+\color{blue}{\left(\dfrac{1}{2}\cdot\dfrac{5}{3}\right)^2}&\color{black}{\text{Simplify }}c \\ x^2+\dfrac{5}{3}x+\color{blue}{\dfrac{25}{36}}&\color{black}{\text{Perfect square polynomial}}\end{array}\nonumber\]
Thus, \(c=\dfrac{25}{36}\). Rewriting this perfect square trinomial in factored form, we get
\[x^2+\dfrac{5}{3}x+\color{blue}{\dfrac{25}{36}}\color{black}{=}\left(x+\dfrac{5}{6}\right)^2\nonumber\]
The Chinese in 200 BC were the first known culture group to use a method similar to completing the square, but their method was only used to calculate positive roots.
Given a quadratic equation \(x^2 + bx + c = 0\), we can use the following method to solve for \(x\).
Step 1. Rewrite the quadratic equation so that the coefficient of the leading term is one, and the original constant coefficient is on the opposite side of the equal sign from the leading and linear terms.
Step 2. Complete the square, i.e., \(\left(\dfrac{b}{2}\right)^2\) or \(\left(\dfrac{1}{2}b\right)^2\), and add the result to both sides of the quadratic equation.
Step 3. Rewrite the perfect square trinomial in factored form.
Step 4. Solve using the square root property.
Step 5. Verify the solution(s).
Solve Quadratic Equations by Completing the Square, \(a=1\)
Recall. When the leading coefficient is one, i.e., \(a = 1\), of the quadratic equation \(ax^2 + bx + c = 0\), we have the quadratic equation \(x^2 + bx + c = 0\).
Solve: \(x^2+10x=-24\)
Solution
Step 1. Rewrite the quadratic equation so that the coefficient of the leading term is one, and the original constant coefficient is on the opposite side of the equal sign from the leading and linear terms. Notice, the first step is done for us: \[x^2+10x=-24\nonumber\]
Step 2. Complete the square, i.e., \(\left(\dfrac{b}{2}\right)^2\) or \(\left(\dfrac{1}{2}b\right)^2\), and add the result to both sides of the quadratic equation. \[\begin{array}{rl} x^2+10x=-24 &b=10;\text{ apply formula }\left(\dfrac{b}{2}\right)^2 \\ x^2+10x+\color{blue}{\left(\dfrac{10}{2}\right)^2}\color{black}{=}-24+\color{blue}{\left(\dfrac{10}{2}\right)^2}&\color{black}{\text{Simplify}} \\ x^2+10x+\color{blue}{25}\color{black}{=}-24+\color{blue}{25}&\color{black}{\text{Perfect square trinomial}}\end{array}\nonumber\]
Step 3. Rewrite the perfect square trinomial in factored form. \[\begin{array}{rl}x^2+10x+25=-24+25 &\text{Perfect square trinomial} \\ (x+5)^2=1 &\text{Factored form}\end{array}\nonumber\]
Step 4. Solve using the square root property. \[\begin{array}{rl} (x+5)^2=1&\text{Apply the square root property} \\ x+5=\pm\sqrt{1}&\text{Isolate the variable} \\ x=-5\pm\sqrt{1}&\text{Rewrite as two solutions} \\ x=-5+1\text{ or }x=-5-1&\text{Evaluate} \\ x=-4\text{ or }x=-6&\text{Solution}\end{array}\nonumber\]
Step 5. Verify the solution(s). \[\begin{array}{rl}x^2+10x=-24&x^2+10x=-24\quad \\ \color{blue}{(-4)}\color{black}{^2}+10\color{blue}{(-4)}\color{black}{\stackrel{?}{=}}-24&\color{blue}{(-6)}\color{black}{^2}+10\color{blue}{(-6)}\color{black}{\stackrel{?}{=}}-24\quad \\ 16-40\stackrel{?}{=}-24&36-60\stackrel{?}{=}-24\quad \\ -24=-24\:\checkmark & -24=-24\:\checkmark \end{array}\nonumber\]
Thus, \(x = −4\) and \(x = −6\) are the solutions.
Solve: \(n^2+8n+4=0\)
Solution
Step 1. Rewrite the quadratic equation so that the coefficient of the leading term is one, and the original constant coefficient is on the opposite side of the equal sign from the leading and linear terms. \[\begin{aligned}n^2+8n+4&=0 \\ n^2+8n&=-4\end{aligned}\]
Step 2. Complete the square, i.e., \(\left(\dfrac{b}{2}\right)^2\) or \(\left(\dfrac{1}{2}b\right)^2\), and add the result to both sides of the quadratic equation. \[\begin{array}{rl}n^2-8n=-4 &b=-8;\text{ apply formula }\left(\dfrac{b}{2}\right)^2 \\ n^2-8n+\color{blue}{\left(\dfrac{-8}{2}\right)^2}\color{black}{=}-4+\color{blue}{\left(\dfrac{-8}{2}\right)^2}&\color{black}{\text{Simplify}} \\ n^2-8n+\color{blue}{16}\color{black}{=}-4+\color{blue}{16}&\color{black}{\text{Perfect square trinomial}}\end{array}\nonumber\]
Step 3. Rewrite the perfect square trinomial in factored form. \[\begin{array}{rl} n^2-8n+16=-4+16&\text{Perfect square trinomial} \\ (n-4)^2=12&\text{Factored form}\end{array}\nonumber\]
Step 4. Solve using the square root property. \[\begin{array}{rl}(n-4)^2=12 &\text{Apply the square root property} \\ n-4=\pm\sqrt{12}&\text{Isolate the variable} \\ n=4\pm\sqrt{12}&\text{Simplify }\sqrt{12} \\ n=4\pm\sqrt{4\cdot 3}&\text{Apply product property for radicals} \\ n=4\pm 2\sqrt{3}&\text{Solution}\end{array}\nonumber\]
Step 5. Verify the solution(s). We leave this step to the student.
Thus, \(n=4+2\sqrt{3}\) and \(n=4-2\sqrt{3}\) are the solutions.
Solve Quadratic Equations by Completing the Square, \(a\neq 1\)
Solve: \(3x^2-36x+60=0\)
Solution
Step 1. Rewrite the quadratic equation so that the coefficient of the leading term is one, and the original constant coefficient is on the opposite side of the equal sign from the leading and linear terms. \[\begin{aligned} 3x^2-36x+60&=0 \\ 3x^2-36x&=-60 \\ \color{blue}{3}\color{black}{(}x^2-12x)&=\color{blue}{3}\color{black}{\cdot}-20 \\ \color{black}{\cancel{\color{blue}{3}}}\color{black}{(}x^2-12x)&=\color{black}{\cancel{\color{blue}{3}}}\color{black}{\cdot}-20 \\ x^2-12x&=-20\end{aligned}\]
Step 2. Complete the square, i.e., \(\left(\dfrac{b}{2}\right)^2\) or \(\left(\dfrac{1}{2}b\right)^2\), and add the result to both sides of the quadratic equation. \[\begin{array}{rl}x^2-12x=-20 &b=-12;\text{ apply formula }\left(\dfrac{b}{2}\right)^2 \\ x^2-12x+\color{blue}{\left(\dfrac{-12}{2}\right)^2}\color{black}{=}-20+\color{blue}{\left(\dfrac{-12}{2}\right)^2}&\color{black}{\text{Simplify}} \\ x^2-12x+\color{blue}{36}\color{black}{=}-20+\color{blue}{36}&\color{black}{\text{Perfect square trinomial}}\end{array}\nonumber\]
Step 3. Rewrite the perfect square trinomial in factored form. \[\begin{array}{rl}x^2-12x+36=-20+36&\text{Perfect square trinomial} \\ (x-6)^2=16&\text{Factored form}\end{array}\nonumber\]
Step 4. Solve using the square root property. \[\begin{array}{rl}(x-6)^2=16&\text{Apply the square root property} \\ x-6=\pm\sqrt{16}&\text{Isolate the variable} \\ x=6\pm\sqrt{16}&\text{Rewrite as two solutions} \\ x=6+4\text{ or }x=6-4&\text{Evaluate} \\ x=10\text{ or }x=2&\text{Solution}\end{array}\nonumber\]
Step 5. Verify the solution(s). We leave this step to the student.
Thus, \(x=10\) and \(x=2\) are the solutions.
Solve: \(2k^2+k-2=0\)
Solution
Step 1. Rewrite the quadratic equation so that the coefficient of the leading term is one, and the original constant coefficient is on the opposite side of the equal sign from the leading and linear terms. \[\begin{aligned} 2k^2+k-2&=0 \\ 2k^2+k&=2 \\ \color{blue}{2}\color{black}{}\left(k^2+\dfrac{1}{2}k\right)&=\color{blue}{2}\color{black}{\:\cdot}1 \\ \color{black}{\cancel{\color{blue}{2}}}\color{black}{}\left(k^2+\dfrac{1}{2}k\right)&=\color{black}{\cancel{\color{blue}{2}}}\color{black}{\:\cdot} 1 \\ k^2+\dfrac{1}{2}k&=1\end{aligned}\]
Step 2. Complete the square, i.e., \(\left(\dfrac{b}{2}\right)^2\) or \(\left(\dfrac{1}{2}b\right)^2\), and add the result to both sides of the quadratic equation. \[\begin{array}{rl} k^2+\dfrac{1}{2}k=1 &b=\dfrac{1}{2};\text{ apply formula }\left(\dfrac{1}{2}b\right)^2 \\ k^2+\dfrac{1}{2}k+\color{blue}{\left(\dfrac{1}{2}\cdot\dfrac{1}{2}\right)^2}\color{black}{=}1+\color{blue}{\left(\dfrac{1}{2}\cdot\dfrac{1}{2}\right)^2}&\color{black}{\text{Simplify}} \\ k^2+\dfrac{1}{2}k+\color{blue}{\dfrac{1}{16}}\color{black}{=}1+\color{blue}{\dfrac{1}{16}}&\color{black}{\text{Perfect square trinomial}}\end{array}\nonumber\]
Step 3. Rewrite the perfect square trinomial in factored form. \[\begin{array}{rl}k^2+\dfrac{1}{2}k+\dfrac{1}{16}=1+\dfrac{1}{16}&\text{Perfect square trinomial} \\ \left(k+\dfrac{1}{4}\right)^2=\dfrac{17}{16}&\text{Factored form}\end{array}\nonumber\]
Step 4. Solve using the square root property. \[\begin{array}{rl}\left(k+\dfrac{1}{4}\right)^2=\dfrac{17}{16}&\text{Apply the square root property} \\ k+\dfrac{1}{4}=\pm\sqrt{\dfrac{17}{16}}&\text{Isolate the variable} \\ k=-\dfrac{1}{4}\pm\sqrt{\dfrac{17}{16}}&\text{Simplify }\sqrt{\dfrac{17}{16}} \\ k=-\dfrac{1}{4}\pm\dfrac{\sqrt{14}}{4}&\text{Same denominator, combine fractions} \\ k=\dfrac{-1\pm\sqrt{17}}{4}&\text{Solution}\end{array}\nonumber\]
Step 5. Verify the solution(s). We leave this step to the student.
Thus, \(\dfrac{-1+\sqrt{17}}{4}\) and \(\dfrac{-1-\sqrt{17}}{4}\) are the solutions.
Completing the Square Homework
Complete the square and rewrite in factored form.
\(x^2-30x+\underline{\quad}\)
\(m^2-36m+\underline{\quad}\)
\(x^2-15x+\underline{\quad}\)
\(y^2-y+\underline{\quad}\)
\(a^2-24a+\underline{\quad}\)
\(x^2-34x+\underline{\quad}\)
\(r^2-\dfrac{1}{9}r+\underline{\quad}\)
\(p^2-17p+\underline{\quad}\)
Solve each equation by completing the square.
\(x^2-16x+55=0\)
\(v^2-8v+45=0\)
\(6x^2+12x+63=0\)
\(5k^2-10k+48=0\)
\(x^2+10x-57=4\)
\(n^2-16n+67=4\)
\(2x^2+4x+38=-6\)
\(8b^2+16b-37=5\)
\(x^2=-10x-29\)
\(n^2=-21+10n\)
\(3k^2+9=6k\)
\(2x^2+63=8x\)
\(p^2-8p=-55\)
\(7n^2-n+7=7n+6n^2\)
\(13b^2+15b+44=-5+7b^2+3b\)
\(5x^2+5x=-31-5x\)
\(v^2+5v+28=0\)
\(7x^2-6x+40=0\)
\(k^2-7k+50=3\)
\(5x^2+8x-40=8\)
\(m^2=-15+9m\)
\(8r^2+10r=-55\)
\(-2x^2+3x-5=-4x^2\)
\(5n^2-8n+60=-3n+6+4n^2\)
\(n^2-8n-12=0\)
\(b^2+2b+43=0\)
\(3x^2-6x+47=0\)
\(8a^2+16a-1=0\)
\(p^2-16p-52=0\)
\(m^2-8m-3=0\)
\(6r^2+12r-24=-6\)
\(6n^2-12n-14=4\)
\(v^2=14v+36\)
\(a^2-56=-10a\)
\(5x^2=-26+10x\)
\(5n^2=-10n+15\)
\(x^2+8x+15=8\)
\(n^2+4n=12\)
\(-3r^2+12r+49=-6r^2\)
\(8n^2+16n=64\)
\(b^2+7b-33=0\)
\(4x^2+4x+25=0\)
\(a^2-5a+25=3\)
\(2p^2-p+56=-8\)
\(n^2-n=-41\)
\(3x^2-11x=-18\)
\(4b^2-15b+56=3b^2\)
\(10v^2-15v=27+4v^2-6v\)


