9.6: Counting Principles
- Last updated
- Save as PDF
- Page ID
- 15108
Learning Objectives
- Solve counting problems using the Addition Principle.
- Solve counting problems using the Multiplication Principle.
- Solve counting problems using permutations involving n distinct objects.
- Solve counting problems using combinations.
- Find the number of subsets of a given set.
- Solve counting problems using permutations involving n non-distinct objects.
A new company sells customizable cases for tablets and smartphones. Each case comes in a variety of colors and can be personalized for an additional fee with images or a monogram. A customer can choose not to personalize or could choose to have one, two, or three images or a monogram. The customer can choose the order of the images and the letters in the monogram. The company is working with an agency to develop a marketing campaign with a focus on the huge number of options they offer. Counting the possibilities is challenging!
We encounter a wide variety of counting problems every day. There is a branch of mathematics devoted to the study of counting problems such as this one. Other applications of counting include secure passwords, horse racing outcomes, and college scheduling choices. We will examine this type of mathematics in this section.
Using the Addition Principle
The company that sells customizable cases offers cases for tablets and smartphones. There are \(3\) supported tablet models and \(5\) supported smartphone models. The Addition Principle tells us that we can add the number of tablet options to the number of smartphone options to find the total number of options. By the Addition Principle, there are \(8\) total options, as we can see in Figure \(\PageIndex{1}\).
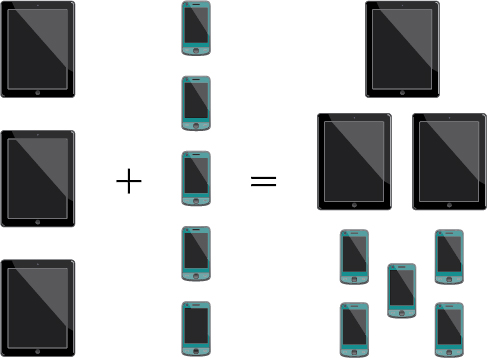
Figure \(\PageIndex{1}\)
THE ADDITION PRINCIPLE
According to the Addition Principle, if one event can occur in \(m\) ways and a second event with no common outcomes can occur in \(n\) ways, then the first or second event can occur in \(m+n\) ways.
Example \(\PageIndex{1}\): Using the Addition Principle
There are \(2\) vegetarian entrée options and \(5\) meat entrée options on a dinner menu. What is the total number of entrée options?
Solution
We can add the number of vegetarian options to the number of meat options to find the total number of entrée options.

There are \(7\) total options.
Exercise \(\PageIndex{1}\)
A student is shopping for a new computer. He is deciding among \(3\) desktop computers and \(4\) laptop computers. What is the total number of computer options?
- Answer
-
\(7\)
Using the Multiplication Principle
The Multiplication Principle applies when we are making more than one selection. Suppose we are choosing an appetizer, an entrée, and a dessert. If there are \(2\) appetizer options, \(3\) entrée options, and \(2\) dessert options on a fixed-price dinner menu, there are a total of \(12\) possible choices of one each as shown in the tree diagram in Figure \(\PageIndex{2}\).
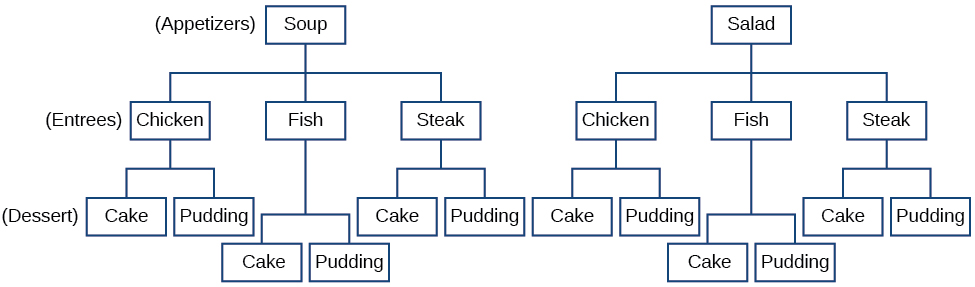
Figure \(\PageIndex{2}\)
The possible choices are:
- soup, chicken, cake
- soup, chicken, pudding
- soup, fish, cake
- soup, fish, pudding
- soup, steak, cake
- soup, steak, pudding
- salad, chicken, cake
- salad, chicken, pudding
- salad, fish, cake
- salad, fish, pudding
- salad, steak, cake
- salad, steak, pudding We can also find the total number of possible dinners by multiplying.
We could also conclude that there are \(12\) possible dinner choices simply by applying the Multiplication Principle.
\(\# \text{of appetizer options} \times \# \text {of entree options} \times \# \text {of dessert options}\)
\(2 × 3 × 2=12\)
THE MULTIPLICATION PRINCIPLE
According to the Multiplication Principle, if one event can occur in \(m\) ways and a second event can occur in \(n\) ways after the first event has occurred, then the two events can occur in \(m×n\) ways. This is also known as the Fundamental Counting Principle.
Example \(\PageIndex{2}\): Using the Multiplication Principle
Diane packed \(2\) skirts, \(4\) blouses, and a sweater for her business trip. She will need to choose a skirt and a blouse for each outfit and decide whether to wear the sweater. Use the Multiplication Principle to find the total number of possible outfits.
Solution
To find the total number of outfits, find the product of the number of skirt options, the number of blouse options, and the number of sweater options.

There are \(16\) possible outfits.
Exercise \(\PageIndex{2}\)
A restaurant offers a breakfast special that includes a breakfast sandwich, a side dish, and a beverage. There are \(3\) types of breakfast sandwiches, \(4\) side dish options, and \(5\) beverage choices. Find the total number of possible breakfast specials.
- Answer
-
There are \(60\) possible breakfast specials.
Finding the Number of Permutations of \(n\) Distinct Objects
The Multiplication Principle can be used to solve a variety of problem types. One type of problem involves placing objects in order. We arrange letters into words and digits into numbers, line up for photographs, decorate rooms, and more. An ordering of objects is called a permutation.
Finding the Number of Permutations of \(n\) Distinct Objects Using the Multiplication Principle
To solve permutation problems, it is often helpful to draw line segments for each option. That enables us to determine the number of each option so we can multiply. For instance, suppose we have four paintings, and we want to find the number of ways we can hang three of the paintings in order on the wall. We can draw three lines to represent the three places on the wall.

There are four options for the first place, so we write a \(4\) on the first line.

After the first place has been filled, there are three options for the second place so we write a \(3\) on the second line.
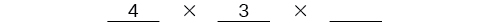
After the second place has been filled, there are two options for the third place so we write a \(2\) on the third line. Finally, we find the product.
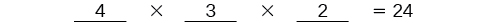
There are \(24\) possible permutations of the paintings.
How to: Given \(n\) distinct options, determine how many permutations there are.
- Determine how many options there are for the first situation.
- Determine how many options are left for the second situation.
- Continue until all of the spots are filled.
- Multiply the numbers together.
Example \(\PageIndex{3}\): Finding the Number of Permutations Using the Multiplication Principle
At a swimming competition, nine swimmers compete in a race.
- How many ways can they place first, second, and third?
- How many ways can they place first, second, and third if a swimmer named Ariel wins first place? (Assume there is only one contestant named Ariel.)
- How many ways can all nine swimmers line up for a photo?
Solution
- Draw lines for each place.
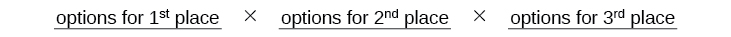
There are \(9\) options for first place. Once someone has won first place, there are \(8\) remaining options for second place. Once first and second place have been won, there are \(7\) remaining options for third place.
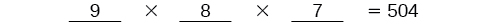
Multiply to find that there are \(504\) ways for the swimmers to place.
- Draw lines for describing each place.
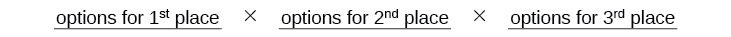
We know Ariel must win first place, so there is only \(1\) option for first place. There are \(8\) remaining options for second place, and then \(7\) remaining options for third place.
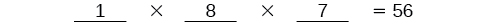
Multiply to find that there are \(56\) ways for the swimmers to place if Ariel wins first.
- Draw lines for describing each place in the photo.

There are \(9\) choices for the first spot, then \(8\) for the second, \(7\) for the third, \(6\) for the fourth, and so on until only \(1\) person remains for the last spot.
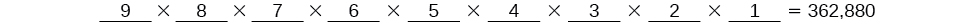
There are \(362,880\) possible permutations for the swimmers to line up.
Analysis
Note that in part c, we found there were \(9!\) ways for \(9\) people to line up. The number of permutations of \(n\) distinct objects can always be found by \(n!\).
Exercise \(\PageIndex{3A}\)
A family of five is having portraits taken. Use the Multiplication Principle to find the following:
- How many ways can the family line up for the portrait?
- How many ways can the photographer line up \(3\) family members?
- How many ways can the family line up for the portrait if the parents are required to stand on each end?
- Answer a
-
\(120\)
- Answer b
-
\(60\)
- Answer c
-
\(12\)
Finding the Number of Permutations of n Distinct Objects Using a Formula
For some permutation problems, it is inconvenient to use the Multiplication Principle because there are so many numbers to multiply. Fortunately, we can solve these problems using a formula. Before we learn the formula, let’s look at two common notations for permutations. If we have a set of \(n\) objects and we want to choose \(r\) objects from the set in order, we write \(P(n,r)\). Another way to write this is \(nP_r\), a notation commonly seen on computers and calculators. To calculate \(P(n,r)\), we begin by finding \(n!\), the number of ways to line up all nn objects. We then divide by \((n−r)!\) to cancel out the \((n−r)\) items that we do not wish to line up.
Let’s see how this works with a simple example. Imagine a club of six people. They need to elect a president, a vice president, and a treasurer. Six people can be elected president, any one of the five remaining people can be elected vice president, and any of the remaining four people could be elected treasurer. The number of ways this may be done is \(6×5×4=120\). Using factorials, we get the same result.
\(\dfrac{6!}{3!}=\dfrac{6·5·4·3!}{3!}=6·5·4=120 \)
There are \(120\) ways to select \(3\) officers in order from a club with \(6\) members. We refer to this as a permutation of \(6\) taken \(3\) at a time. The general formula is as follows.
\[P(n,r)=\dfrac{n!}{(n−r)!}\]
Note that the formula stills works if we are choosing all \(n\) objects and placing them in order. In that case we would be dividing by \((n−n)!\) or \(0!\), which we said earlier is equal to \(1\). So the number of permutations of \(n\) objects taken \(n\) at a time is \(\dfrac{n!}{1}\) or just \(n!\).
Note: FORMULA FOR PERMUTATIONS OF N DISTINCT OBJECTS
Given \(n\) distinct objects, the number of ways to select \(r\) objects from the set in order is
\[P(n,r)=\dfrac{n!}{(n−r)!}\]
How to: Given a word problem, evaluate the possible permutations.
- Identify \(n\) from the given information.
- Identify \(r\) from the given information.
- Replace \(n\) and \(r\) in the formula with the given values.
- Evaluate.
Example \(\PageIndex{4}\): Finding the Number of Permutations Using the Formula
A professor is creating an exam of \(9\) questions from a test bank of \(12\) questions. How many ways can she select and arrange the questions?
Solution
Substitute \(n=12\) and \(r=9\) into the permutation formula and simplify.
\[\begin{align*} P(n,r)&=\dfrac{n!}{(n-r)!}\\ P(12,9)&=\dfrac{12!}{(12-9)!}\\ &=\dfrac{12!}{3!}\\ &=79,833,600 \end{align*}\]
There are \(79,833,600\) possible permutations of exam questions!
Analysis
We can also use a calculator to find permutations. For this problem, we would enter \(12\), press the \(nP_r\) function, enter \(9\), and then press the equal sign. The \(nP_r\) function may be located under the MATH menu with probability commands.
Q&A
Could we have solved the example above using the Multiplication Principle?
Yes. We could have multiplied \(15⋅14⋅13⋅12⋅11⋅10⋅9⋅8⋅7⋅6⋅5⋅4\) to find the same answer.
Exercise \(\PageIndex{4A}\)
A play has a cast of \(7\) actors preparing to make their curtain call. Use the permutation formula to find the following.
How many ways can the \(7\) actors line up?
- Answer
-
\(P(7,7)=5,040\)
Exercise \(\PageIndex{4B}\)
How many ways can \(5\) of the \(7\) actors be chosen to line up?
- Answer
-
\(P(7,5)=2,520\)
Find the Number of Combinations Using the Formula
So far, we have looked at problems asking us to put objects in order. There are many problems in which we want to select a few objects from a group of objects, but we do not care about the order. When we are selecting objects and the order does not matter, we are dealing with combinations. A selection of \(r\) objects from a set of \(n\) objects where the order does not matter can be written as \(C(n,r)\). Just as with permutations, \(C(n,r)\) can also be written as \(nC_r\). In this case, the general formula is as follows.
\[C(n,r)=\dfrac{n!}{r!(n−r)!} \label{combo}\]
An earlier problem considered choosing \(3\) of \(4\) possible paintings to hang on a wall. We found that there were \(24\) ways to select \(3\) of the \(4\) paintings in order. But what if we did not care about the order? We would expect a smaller number because selecting paintings \(1, 2, 3\) would be the same as selecting paintings \(2, 3, 1\). To find the number of ways to select \(3\) of the \(4\) paintings, disregarding the order of the paintings, divide the number of permutations by the number of ways to order \(3\) paintings. There are \(3!=3·2·1=6\) ways to order \(3\) paintings. There are \(\dfrac{24}{6}\), or \(4\) ways to select \(3\) of the \(4\) paintings. This number makes sense because every time we are selecting \(3\) paintings, we are not selecting \(1\) painting. There are \(4\) paintings we could choose not to select, so there are \(4\) ways to select \(3\) of the \(4\) paintings.
Note: FORMULA FOR COMBINATIONS OF N DISTINCT OBJECTS
Given \(n\) distinct objects, the number of ways to select \(r\) objects from the set is
\[C(n,r)=\dfrac{n!}{r!(n−r)!}\]
How to: Given a number of options, determine the possible number of combinations.
- Identify \(n\) from the given information.
- Identify \(r\) from the given information.
- Replace \(n\) and \(r\) in the formula with the given values.
- Evaluate.
Example \(\PageIndex{5}\): Finding the Number of Combinations Using the Formula
A fast food restaurant offers five side dish options. Your meal comes with two side dishes.
- How many ways can you select your side dishes?
- How many ways can you select \(3\) side dishes?
Solution
- We want to choose \(2\) side dishes from \(5\) options.
\(C(5,2)=\dfrac{5!}{2!(5−2)!}=10\)
- We want to choose \(3\) side dishes from \(5\) options.
\(C(5,3)=\dfrac{5!}{3!(5−3)!}=10\)
Analysis
We can also use a graphing calculator to find combinations. Enter 5, then press \(nC_r\), enter 3, and then press the equal sign. The \(nC_r\), function may be located under the MATH menu with probability commands.
Q&A
Is it a coincidence that parts (a) and (b) in the example above have the same answers?
No. When we choose r objects from n objects, we are not choosing \((n–r)\) objects. Therefore, \(C(n,r)=C(n,n–r)\).
Exercise \(\PageIndex{5}\)
An ice cream shop offers \(10\) flavors of ice cream. How many ways are there to choose \(3\) flavors for a banana split?
- Answer
-
\(C(10,3)=120\)
Finding the Number of Subsets of a Set
We have looked only at combination problems in which we chose exactly rr objects. In some problems, we want to consider choosing every possible number of objects. Consider, for example, a pizza restaurant that offers \(5\) toppings. Any number of toppings can be ordered. How many different pizzas are possible?
To answer this question, we need to consider pizzas with any number of toppings. There is \(C(5,0)=1\) way to order a pizza with no toppings. There are \(C(5,1)=5\) ways to order a pizza with exactly one topping. If we continue this process, we get
\(C(5,0)+C(5,1)+C(5,2)+C(5,3)+C(5,4)+C(5,5)=32\)
There are \(32\) possible pizzas. This result is equal to \(2^5\).
We are presented with a sequence of choices. For each of the nn objects we have two choices: include it in the subset or not. So for the whole subset we have made nn choices, each with two options. So there are a total of \(2·2·2·…·2\) possible resulting subsets, all the way from the empty subset, which we obtain when we say “no” each time, to the original set itself, which we obtain when we say “yes” each time.
Note: FORMULA FOR THE NUMBER OF SUBSETS OF A SET
A set containing n distinct objects has \(2^n\) subsets.
Example \(\PageIndex{6}\): Finding the Number of Subsets of a Set
A restaurant offers butter, cheese, chives, and sour cream as toppings for a baked potato. How many different ways are there to order a potato?
Solution
We are looking for the number of subsets of a set with \(4\) objects. Substitute \(n=4\) into the formula.
\[\begin{align*} 2^n&=2^4\\ &=16 \end{align*}\]
There are \(16\) possible ways to order a potato.
Exercise \(\PageIndex{6}\)
A sundae bar at a wedding has \(6\) toppings to choose from. Any number of toppings can be chosen. How many different sundaes are possible?
- Answer
-
\(64\) sundaes
Finding the Number of Permutations of n Non-Distinct Objects
We have studied permutations where all of the objects involved were distinct. What happens if some of the objects are indistinguishable? For example, suppose there is a sheet of \(12\) stickers. If all of the stickers were distinct, there would be \(12!\) ways to order the stickers. However, \(4\) of the stickers are identical stars, and \(3\) are identical moons. Because all of the objects are not distinct, many of the \(12!\) permutations we counted are duplicates. The general formula for this situation is as follows.
\[\dfrac{n!}{r_1!r_2!…r_k!}\]
In this example, we need to divide by the number of ways to order the \(4\) stars and the ways to order the \(3\) moons to find the number of unique permutations of the stickers. There are \(4!\) ways to order the stars and \(3!\) ways to order the moon.
\(\dfrac{12!}{4!3!}=3,326,400\)
There are \(3,326,400\) ways to order the sheet of stickers.
Note: FORMULA FOR FINDING THE NUMBER OF PERMUTATIONS OF \(N\) NON-DISTINCT OBJECTS
If there are nn elements in a set and \(r_1\) are alike, \(r_2\) are alike, \(r_3\) are alike, and so on through \(r_k\), the number of permutations can be found by
\[\dfrac{n!}{r_1!r_2!…r_k!}\]
Example \(\PageIndex{7}\): Finding the Number of Permutations of \(n\) Non-Distinct Objects
Find the number of rearrangements of the letters in the word DISTINCT.
Solution
There are \(8\) letters. Both \(I\) and \(T\) are repeated \(2\) times. Substitute \(n=8\), \(r_1=2\), and \(r_2=2\) into the formula.
\(\dfrac{8!}{2!2!}=10,080\)
There are \(10,080\) arrangements.
Exercise \(\PageIndex{7}\)
Find the number of rearrangements of the letters in the word CARRIER.
- Answer
-
\(840\)
Media
Access these online resources for additional instruction and practice with combinations and permutations.
Key Equations
| number of permutations of \(n\) distinct objects taken \(r\) at a time | \(P(n,r)=\dfrac{n!}{(n−r)!}\) |
| number of combinations of \(n\) distinct objects taken \(r\) at a time | \(C(n,r)=\dfrac{n!}{r!(n−r)!}\) |
| number of permutations of \(n\) non-distinct objects | \(\dfrac{n!}{r1!r2!…rk!}\) |
Key Concepts
- If one event can occur in \(m\) ways and a second event with no common outcomes can occur in \(n\) ways, then the first or second event can occur in \(m+n\) ways. See Example \(\PageIndex{1}\).
- If one event can occur in \(m\) ways and a second event can occur in \(n\) ways after the first event has occurred, then the two events can occur in \(m×n\) ways. See Example \(\PageIndex{2}\).
- A permutation is an ordering of \(n\) objects.
- If we have a set of \(n\) objects and we want to choose \(r\) objects from the set in order, we write \(P(n,r)\).
- Permutation problems can be solved using the Multiplication Principle or the formula for \(P(n,r)\). See Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\).
- A selection of objects where the order does not matter is a combination.
- Given \(n\) distinct objects, the number of ways to select \(r\) objects from the set is \(C(n,r)\) and can be found using a formula. See Example \(\PageIndex{5}\).
- A set containing \(n\) distinct objects has \(2n\) subsets. See Example \(\PageIndex{6}\).
- For counting problems involving non-distinct objects, we need to divide to avoid counting duplicate permutations. See Example \(\PageIndex{7}\).
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


