1.2: Graphs and Symmetry

Last updated

Oct 6, 2021
Save as PDF
- 1.1: Functions and Graphs
- 1.3: Shifting and Reflecting

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Symmetry (Geometry)

Definition: Symmetric with respect to the y-axis

We say that a graph is symmetric with respect to the y-axis if for every point $(a,b)$ on the graph, there is also a point $(-a,b)$ on the graph; hence $f(x,y) = f(-x,y).$

Visually we have that the y-axis acts as a mirror for the graph. We will demonstrate several functions to test for symmetry graphically using the graphing calculator.

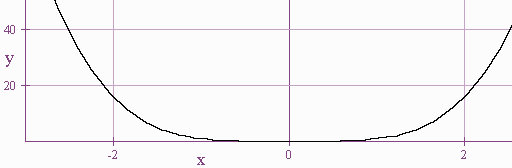
$ysym.gif$

Definition: Symmetric with respect to the x-axis

We say that a graph is symmetric with respect to the x axis if for every point $(a,b)$ on the graph, there is also a point $(a,-b)$ on the graph; hence $f(x,y) = f(x,-y).$

Visually we have that the x-axis acts as a mirror for the graph. We will demonstrate several functions to test for symmetry graphically using the graphing calculator.

Definition: Symmetry with respect to Origin

We say that a graph is symmetric with respect to the origin if for every point $(a,b)$ on the graph, there is also a point $(-a,-b)$ on the graph; hence $f(x,y) = f(-x,-y).$

Visually we have that given a point $P$ on the graph if we draw a line segment $PQ$ through $P$ and the origin such that the origin is the midpoint of $PQ$ , then $Q$ is also on the graph.

$alt$

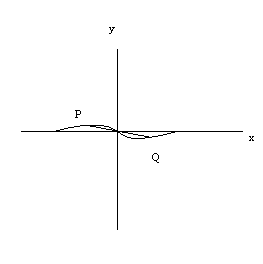
We will use the graphing calculator to test for all three symmetries.

Symmetry (Algebra)

x-axis Symmetry

To test algebraically if a graph is symmetric with respect the x-axis, we replace all the $y$ 's with $-y$ and see if we get an equivalent expression.

Example $\PageIndex{1}$

For

$x - 2y = 5$

we replace with

$x - 2(-y) = 5.$

Simplifying we get

$x+2y=5.$

Which is not equivalent to the original expression. So

$x - 2y = 5$

Is not symmetric with respect to the x-axis.

Example $\PageIndex{2}$

For

$x^3 - y^2 = 2$

we replace with

$x^3 - (-y)^2 = 2$

which is equivalent to the original expression, so that

$x^3 - y^2 = 2$

is symmetric with respect to the x-axis.

y-axis Symmetry

To test algebraically if a graph is symmetric with respect to the y axis, we replace all the x's with -x and see if we get an equivalent expression.

Example $\PageIndex{3}$

For

$y = x^2$

we replace with

$y = (-x)^2 = x^2$

so that

$y = x^2$

is symmetric with respect to the y-axis.

Example $\PageIndex{4}$

For

$y = x^3$

we replace with

$y = (-x)^3 = - x^3$

so that

$y = x^3$

is not symmetric with respect to the y-axis.

Origin Symmetry

To test algebraically if a graph is symmetric with respect to the origin we replace both $x$ and $y$ with $-x$ and $-y$ and see if the result is equivalent to the original expression.

Example $\PageIndex{5}$

For

$y = x^3$

we replace with

$(-y) = (-x)^3$

so that

$-y = -x^3 \text{ or } y=x^3.$

Hence

$y = x^3$

is symmetric with respect to the origin.

Intercepts

We define the x intercepts as the points on the graph where the graph crosses the x axis. If a point is on the x axis, then the y coordinate of the point is 0. Hence to find the x intercepts, we set $y = 0$ and solve.

Example $\PageIndex{6}$ : x intercepts

Find the x intercepts of

$y = x^2+ x - 2$

Solution

We set $y = 0$ so that

$0 = x^2+ x - 2 = (x + 2)(x - 1)$

Hence that x intercepts are at $(-2,0)$ and $(1,0)$

We define the y intercepts of a graph to be the points where the graph crosses the y-axis. At these points the $x$ coordinate is 0 hence to find the y intercepts we set $x = 0$ and find $y$ .

Example $\PageIndex{7}$ : y intercepts

Find the y intercepts of

$y = x^2+ x - 2$

Solution

We set $x = 0$ to get:

$y = 0 + 0 - 2 = -2.$

Hence the y intercept is at $(0,-2)$ .

Contributors and Attributions

Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.

Search

Text Color

Text Size

Margin Size

Font Type

Symmetry (Geometry)

Symmetry (Algebra)

x-axis Symmetry

y-axis Symmetry

Origin Symmetry

Intercepts

Contributors and Attributions

Support Center

How can we help?