1.4: The Complex Plane
- Page ID
- 6469
Geometry of Complex Numbers
Because it takes two numbers \(x\) and \(y\) to describe the complex number \(z = x + iy\) we can visualize complex numbers as points in the \(xy\)-plane. When we do this we call it the complex plane. Since \(x\) is the real part of \(z\) we call the \(x\)-axis the real axis. Likewise, the \(y\)-axis is the imaginary axis.
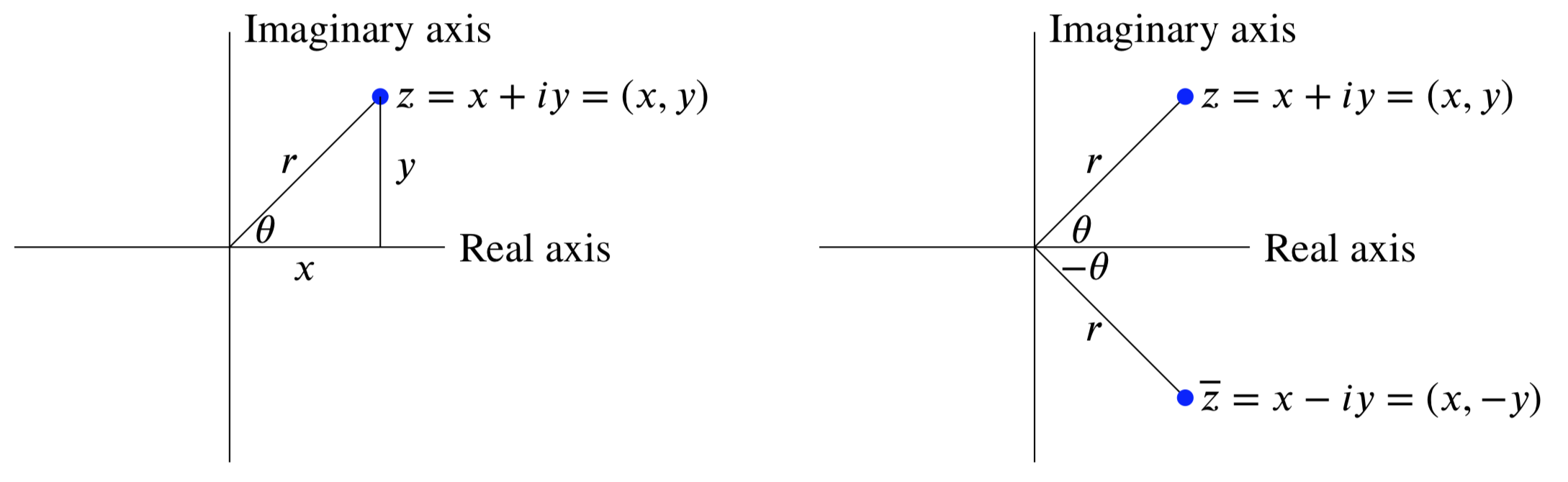
Triangle Inequality
The triangle inequality says that for a triangle the sum of the lengths of any two legs is greater than the length of the third leg.
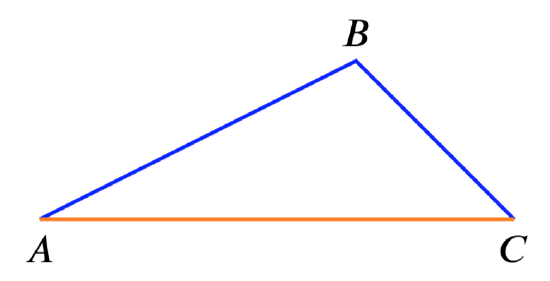
Triangle inequality: \(|AB| + |BC| > |AC|\)
For complex numbers the triangle inequality translates to a statement about complex magnitudes.
Precisely: for complex numbers \(z_1, z_2\)
\[|z_1| + |z_2| \ge |z_1 + z_2| \nonumber \]
with equality only if one of them is 0 or if \(\text{arg}(z_1) = \text{arg}(z_2)\). This is illustrated in the following figure.
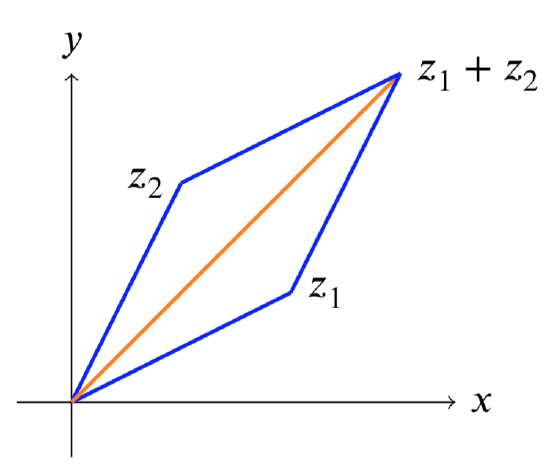
Triangle inequality: \[|z_1| + |z_2| \ge |z_1 + z_2| \nonumber \]
We get equality only if \(z_1\) and \(z_2\) are on the same ray from the origin, i.e. they have the same argument.


